受拉弯扭阶梯轴应力集中系数的有限元分析
蒋 豹,张 强,崔 巍,刘昱良,蒋 婷
(东北石油大学机械科学与工程学院,黑龙江 大庆 163318)
阶梯轴在实际工作中常常发生断裂事故:某减速器齿轮箱在实际运行了约250d后,齿轮轴载联轴器发生断裂事故[1];某石油化工厂在正常运行情况下,高压除焦水泵的泵轴突然发生断裂,引起生产装置停产[2];某45钢减速器轴在使用过程中发生断裂。经分析,发现这些事故都是因轴变径处存在严重的应力集中等因素所引发的[3]。因此,在阶梯轴的设计中,为了减少因应力集中而造成的断裂破坏事故,常常在阶梯轴大小端过渡处设计合理尺寸的圆角。在拉伸、弯曲和扭转等载荷作用下,研究有过渡圆角的阶梯轴的应力集中问题对轴类结构的设计与应用具有重要的意义。
早期人们多采用理论推导的方法来研究应力集中问题。电测法、光弹性法、散斑干涉法、云纹法等实验手段也常被用来研究应力集中问题。随着计算机、有限元法、边界元法的快速发展,学者们开始运用有限元法来研究应力集中问题:张明等[4]对受拉阶梯轴的应力集中问题进行了有限元分析,给出了应力对圆角半径的敏度曲线;陈博等[5]分析了弯曲和扭转载荷下切口参数对轴的应力场强的影响;王正廷等[6]采用有限元法,求出转矩轴卸载槽的理论应力集中系数;马平[7]根据数值解拟合出了扭转载荷作用时轴的各种切口处的应力集中系数公式。
本文使用ANSYS有限元软件,模拟阶梯轴在拉力、扭矩、弯矩作用下的应力集中现象,分析有限元模型中的影响因素,通过实验法验证有限元计算的可靠性。
1 基准应力与应力集中系数
1.1 基准应力
基准应力是根据部件结构形式选取的某个截面上的平均应力。其选取原则有:1)如果造成应力集中的因素不存在,取结构未减小截面上的平均应力;2)如果是多截面结构,取结构最小截面上的平均应力;3)如果结构较长,取远离应力集中处的截面上的平均应力[8]。
本文的基准应力按原则2取阶梯轴小端截面上的平均应力。不同载荷作用下的结构尺寸及力学模型示意图如图1所示,图中D为阶梯轴大端直径,P为轴向拉力,M为弯矩,T为扭矩,d为阶梯轴小端直径。

图1 阶梯轴力学模型示意图
拉伸时基准应力σnom1为
(1)
弯曲时基准应力σnom2为
(2)
扭转时基准应力σnom3为
(3)
1.2 应力集中系数
在实际工程应用中,有些结构必须存在切口、圆角、孔隙等特征,势必造成截面尺寸发生变化。很多学者通过实验和理论分析研究,发现在这些截面发生突变的地方,应力分布不均匀,有应力急剧增大的现象。而这种因为几何尺寸的突变引起应力急剧变化的现象,被称为应力集中[8]。
应力集中处的最大应力值σmax与选取的基准应力σnom的比值,定义为应力集中系数k[9]。
(4)
2 有限元模型
2.1 模型参数
阶梯轴大小端圆轴长度L=200mm,小端直径d=50mm,大端直径D=100mm,圆角半径r=10mm。材料弹性模量E=210GPa,泊松比μ=0.3。
使用ANSYS有限元软件,将阶梯轴离散成solid186结构实体单元,该单元为高阶三维20节点单元,采用二次位移插值形函数,可很好地适应圆角处的曲线边界。圆角处进行局部网格细化,有限元模型如图2所示。
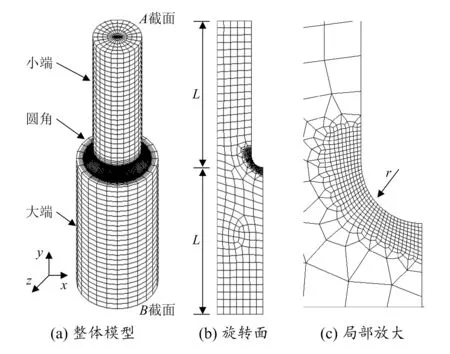
图2 圆轴阶梯轴有限元模型
2.2 载荷及边界条件
边界条件:阶梯轴大端B截面为固定端约束,阶梯轴小端A截面施加载荷。
载荷:基准应力取100MPa,将几何尺寸代入式(1)~式(3),分别求出基准应力对应的拉力、扭矩和弯矩,将载荷施加在阶梯轴小端A截面上,求出过渡圆角处的最大应力,其值除以100便是圆角处的应力集中系数k。
由于实体单元只有3个方向的平动自由度,无法施加力矩。为了施加扭矩和弯矩,根据多点约束方程理论[10],本文采取将阶梯轴A截面上的节点捆绑在A截面中心的导航节点的方法。具体操作是将阶梯轴A截面上的所有节点创建为一个节点组,同时在A截面的中心位置处创建一个新的节点(即导航节点),导航节点具有3个平动和3个转动自由度,然后将之前创建的节点组与导航节点捆绑需要的自由度。如A截面受到轴力作用时,捆绑y方向的平动自由度;分别受到扭矩和弯矩作用时,分别捆绑y和z方向的转动自由度。通过对导航节点施加集中力和集中力矩,实现对实体单元载荷的施加。
3 影响因素分析
为了研究应力集中系数和阶梯轴圆角半径与小端圆轴直径比值的关系,首先需要排除其他因素对应力集中系数的影响。通过分析得出可能的影响因素有局部网格细化等级n、圆周截面份数m和圆轴长度L。下面对这些影响因素进行计算分析。
3.1 局部网格细化等级的影响
图3给出的是在拉力、扭矩和弯矩作用下,阶梯轴圆角网格细化等级n与应力集中系数k的曲线图。从图可以看出,细化等级对拉力作用的应力集中系数影响最大,其次是扭矩,对弯矩作用影响最小。同时可以看出,当n≥2时,应力集中系数都趋于平稳,说明在圆角局部细化时,细化等级的增加不影响应力的大小,所以后续计算时n取为2即可。

图3 圆角网格细化等级的影响
3.2 圆周单元份数的影响
图4给出的是在拉力、弯矩和扭矩作用下,阶梯轴在圆周截面上划分的份数m与应力集中系数k的曲线图。从图可以看出,圆周份数对拉伸应力集中系数没有影响,对扭转和弯曲时的应力集中系数有一定的影响,但当截面圆周份数m≥24时也趋于平稳。综合考虑3种载荷情况,在之后的计算中截面圆周份数m取为24即可。
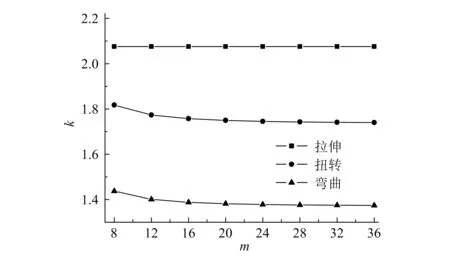
图4 圆周份数的影响
3.3 圆轴长度的影响
图5给出的是不改变直径,在拉力、弯矩和扭矩作用下,圆角的应力集中系数随L/d的变化曲线。从图可以看出,当L/d≤4时,对应力集中系数影响较大,这是因为边界条件对圆角的应力集中情况产生了影响。当L/d>4时,应力集中系数趋于平稳,说明此时边界条件对圆角应力的大小不再产生影响,因此之后的计算中取L/d=4即可。

图5 L/d的影响
4 阶梯轴应力集中分析
在前面影响因素分析的基础上,选取n=2、m=24、L/d=4进行计算。阶梯轴过渡圆角半径r取不同值,阶梯轴小端直径d取50mm,大端直径D取100mm,则轴大、小端的长度L都取为200mm。
4.1 应力集中系数分析
图6给出的是在拉力、弯矩和扭矩作用下阶梯轴圆角处的应力集中系数随r/d变化的曲线,可见随着r/d的增大,应力集中系数逐渐减小,应力集中现象逐渐不明显。

图6 应力集中系数随r/d变化曲线
由图6(a)可见,当r/d=0.010时,应力集中系数实验解[11]为3.524 3,有限元解为3.484 5,误差为1.14%;当r/d=0.030时,应力集中系数实验解为2.851 0,有限元解为2.886 0,误差为1.23%;当r/d=0.100时,实验解为1.965 0,有限元解为2.047 5,误差为4.20%。当r/d≥0.200时,实验解与有限元解最大误差为2.58%,最小误差为0.43%。误差都在5%以内,说明在计算拉力作用下的阶梯轴应力集中系数方面采用有限元方法是合理的。
由图6(b)可见,当r/d=0.030时,实验解[11]为2.374 6,有限元解为2.344 8,误差为1.27%;当r/d=0.100时,实验解为1.802 0,有限元解为1.745 3,误差为3.25%;当r/d>0.100时,实验解与有限元解最大误差为2.51%,最小误差达到0.48%。误差相对较小,即有限元法与实验法比较吻合,说明采用有限元法计算弯矩作用下的阶梯轴应力集中系数是合理的并且精度较高。
由图6(c)可见,因为实验拟合公式有一定的适用范围,所以图中只给出了0.125≤r/d≤0.500的实验解[11]。当r/d=0.125时,实验解为1.682 4,有限元解为1.645 3,误差为2.25%;当r/d≥0.200时,实验解与有限元解最大误差为3.73%,最小误差达到0.86%。误差较小,在允许范围内,说明采用有限元法计算扭矩作用下的阶梯轴应力集中系数也是合理准确的。
因为随着r/d的增加,应力集中系数逐渐减小,所以在对工程结构进行强度校核时,若结构不满足强度要求,可通过适当增大圆弧倒角半径以减小集中应力,使之满足强度要求。
4.2 应力集中位置分析
为了将应力集中的位置表达清楚,绘制如图7所示的应力集中位置示意图。B点为圆角与大圆轴的切点位置,A点为圆角与小圆轴的切点位置,C点为圆弧上任意一点,令BC段弧长为S1,BA段弧长为S,用S1/S表示圆角上任意一点的位置。

图7 圆弧倒角应力集中位置
图8给出的是在拉力、弯矩和扭矩作用下,r/d=0.200时阶梯轴的过渡圆角处的应力云图。图9给出的是不同r/d的阶梯轴,在拉力、弯矩和扭矩作用下过渡圆弧上的应力分布曲线。

图8 r/d=0.200时的过渡圆角处应力云图
从图8剖面图可以看出,应力集中的位置均在阶梯轴小端圆轴表面与过渡圆弧的切点附近,此外还可看出不同载荷作用时最大应力分布的范围大小略有差别。
从图9可以看出,r/d越小最大应力越大,且最大应力在圆弧上分布的范围越大,这样结构破坏的可能性就越大。在图7中以E点表示应力集中的位置,应力集中系数手册[8]中给出应力集中的位置E满足5°≤∠AOE≤10°,即0.89≤S1/S≤0.94。从图9可以看出,3种载荷作用下,不同r/d的应力集中系数都在S1/S=0.89的位置处,即角度∠AOE=5°,与应力集中手册中给出的位置相吻合。

图9 不同r/d时过渡圆弧上的应力分布曲线
4.3 受拉伸和弯曲组合作用
此处以r/d=0.25为例,验证应力集中现象是否符合叠加原理。
图10给出的是拉力、弯矩组合作用和拉力单独作用、弯矩单独作用的应力集中系数随位置变化曲线。可以看出组合作用和单独作用应力集中的位置相同。拉力单独作用时,最大应力为78.543MPa,应力集中系数为0.785;弯矩单独作用时,最大应力为68.323MPa,应力集中系数为0.683;组合作用时,最大应力为146.601MPa,应力集中系数为1.466,等于单独作用的代数和,符合叠加原理。应力云图如图11所示。
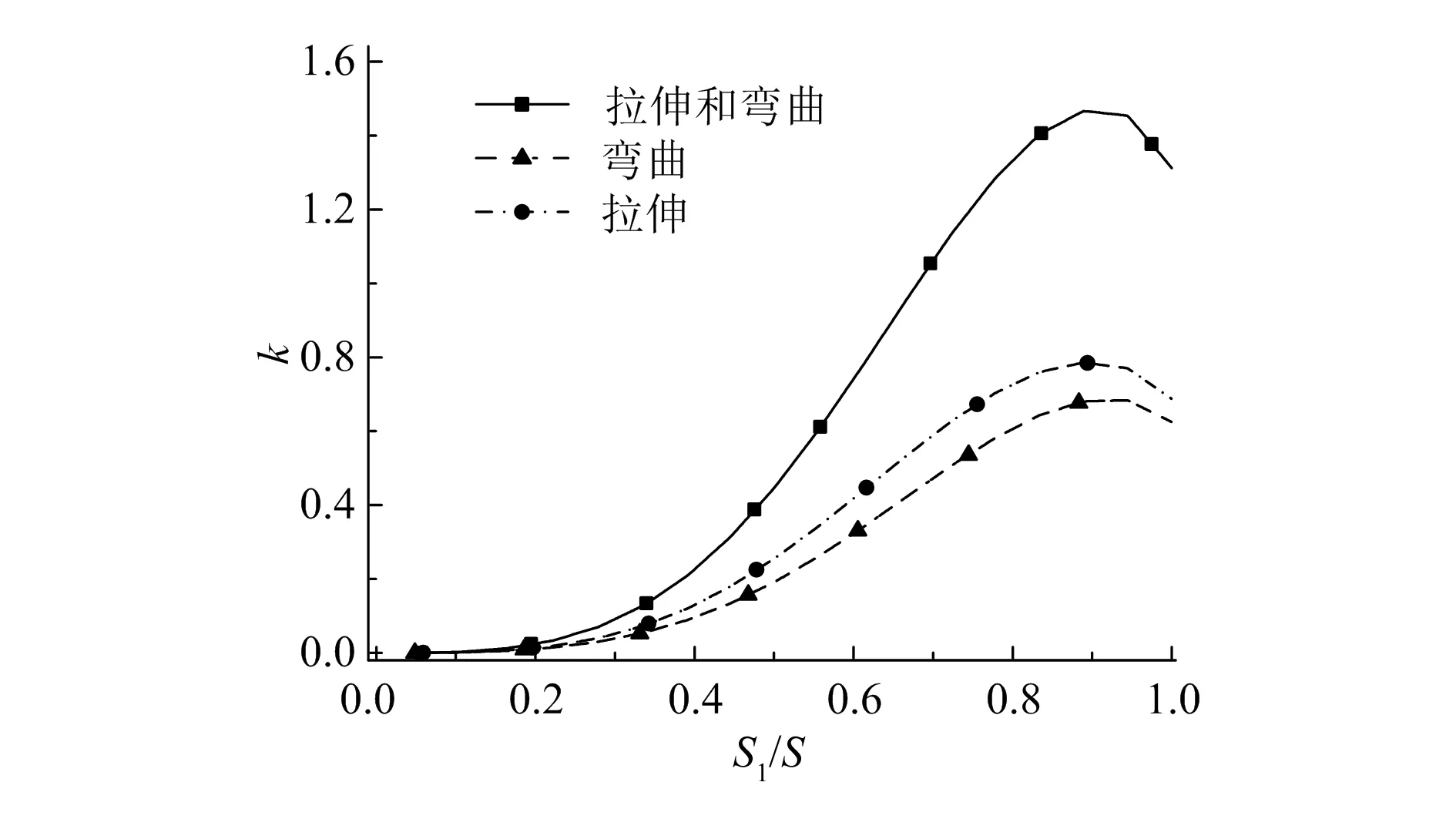
图10 应力集中系数随位置变化曲线

图11 应力云图
5 结论
本文使用有限元法,对阶梯轴过渡圆角应力集中系数进行计算,得出以下结论:
1) 根据多点约束方程理论,实现了实体单元集中力与集中力矩的施加。
2) 分析了拉力、扭矩、弯矩作用下有过渡圆角台肩的应力集中系数的影响因素,得到了应力集中系数与影响因素的关系曲线。
3) 得到了拉伸、扭转、弯曲状态下不同r/d的台肩过渡圆角上不同位置的应力集中系数曲线,可以看出最大应力出现在过渡圆角与小端圆柱切点位置附近。
4) 在排除其他影响因素的条件下,计算了轴力、扭矩、弯矩作用下台肩过渡圆角处的应力集中系数。得到的应力集中系数k与r/d的关系曲线,与应力集中系数手册中的光弹性实验解吻合程度较高,证明了有限元法的准确性,为工程结构设计中应力集中分析提供了一种有效的有限元计算方法。同时,可以通过查找应力集中系数曲线对设计结构进行强度校核,以指导结构设计。

