黄铜动态破坏的热塑性本构模型研究

王晨羽,颜世晶,李金泉

(沈阳理工大学 机械工程学院,沈阳 110159)

材料的本构关系模型是反映材料物理力学行为的数学模型,描述材料应力与应变、应变率与温度等变量之间的关系。目前,针对不同材料和不同实验条件已经得出了很多本构关系。Fields等提出了一种幂指数强化本构模型,求解过程比较简便,但在高温条件下其幂指数增长的特性不能准确描述材料的流变行为[1]。文献[2]提出的Bodner-Partom本构模型,针对材料弹性和塑性变形特性,描述不同材料的力学行为,但参数较多,不宜应用。文献[3]提出的Follansbee-Kocks本构模型,认为应变和初始加工硬化率线性相关,但在高应变率下难以获得精确的模拟结果,同样也存在材料参数过多,使用不方便等缺点。Zerilli-Armstrong本构模型是在材料微观结构的位错力学模型基础上,增加了晶粒尺寸对本构的影响[4]。Johnson-Cook(J-C)模型[5]由于适合大多数金属材料,且结构简单便于应用,因此,获得了广泛的应用,而且针对不同材料产生的误差分别修正了应变强化项[6]、应变率强化项[7]和温度软化项[8-10],得到了改进型的J-C本构模型,使J-C本构模型的应用更加广泛,因此,本文根据霍普金森压杆(SHPB)实验研究黄铜的J-C本构关系模型,实验表明:黄铜的拟合曲线与实验曲线吻合较好,相对误差小于9.38%。

1 试验方法

试验材料为黄铜,进行SHPB试验,试样为圆柱形,尺寸为Φ5mm×5mm,所用子弹长度为140mm,有效气压为0～ 0.60Mpa,温度范围0～ 800℃,应变率范围2000 s-1～ 8000 s-1,将相同的条件进行多次重复试验,取三组有效数据,以此来确保试验结果的可靠性。试样成分见表1。

表1 黄铜的化学成分 wt/%

2 结果与讨论

2.1 本构关系拟合

J-C热塑性本构方程表达式为

(1)

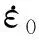
σ(ε)=A+Bεn

(2)

根据常温、准静态下的σ-ε试验数据,当ε=0时的应力值即为参数A,用Matlab软件对数据进行拟合,得到参数B、n的值。

常温下(T=T0),式(1)简化为

(3)

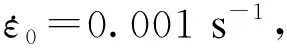
上述参数求得后,由式(1)可得

(4)

依据相应温度下的一系列σ-ε数据,设定一些应变和应变率为已知,可得相对应的应力值表达式,式(4)转变为以T*和m为变量的函数,改变一系列温度,则可拟合出m值。

通过上述计算,得黄铜的本构关系为

(5)

图1为黄铜在5500s-1应变率下,温度分别为25℃、270℃、570℃和790℃时J-C本构模型的拟合曲线与真实应力应变曲线的比较,二者吻合良好。

图1 黄铜的J-C模型曲线和真实应力-应变曲线

2.2 黄铜的动态力学性能分析

为便于比较,将图1中不同温度下的真实应力应变曲线绘在同一张图中,如图2所示。

由图2中可以看出,在较低的温度范围内(25℃～ 270℃),应力随应变的增大而增大,应力变化幅度类似,表现出相似的应变硬化效应,且在该温度范围内应力近似相等,热软化效应不明显;当温度增加到570℃时,应力降低幅度较大,热软化效应明显,但应力仍随应变的增大而增大,仍有应变硬化效应;温度继续增大到790℃时,应力继续降低,且降低幅度较大,热软化效应明显,但应力随应变增大的变化很小,说明高温时黄铜的应变硬化效应较小。图3为不同应变下应力随温度变化的曲线。

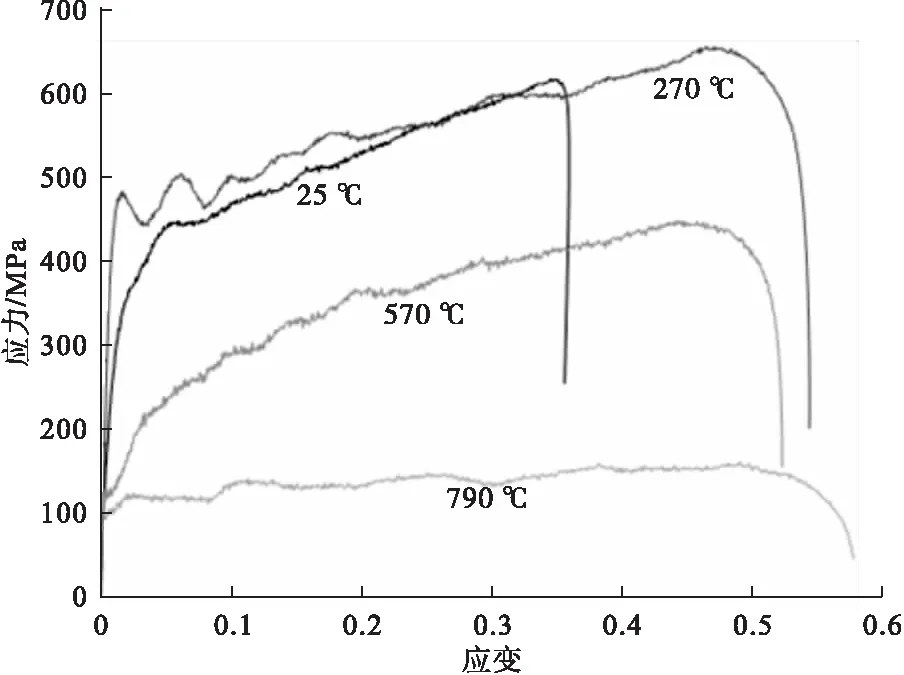
图2 不同温度下真实应力-应变曲线

图3 不同应变下温度对黄铜H62应力的影响

由图3可知在较低温度范围内热软化效应很小;当温度增加到570℃和790℃时,应力降幅非常大,表现出明显的热软化效应;而相同温度下,应变对应力的影响很小,因此,在高温环境下实际应用时,黄铜的工作温度不宜超过270℃。

2.3 本构关系误差分析

为更清楚的反映拟合本构模型的准确性,随机选取每种实验条件下的五组数据,分析其相对误差及误差平均值,如表2 所示。

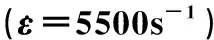
表2 本构模型预测值与实验值的误差

由表2可以看出,表中相对误差均小于10%,同时,黄铜合金不同温度下的平均误差均在5.34%以下。通过误差分析可知,本实验拟合的本构关系准确度较高。

3 结论

(1)利用SHPB装置对黄铜(H62)进行了动态压缩试验,分析了黄铜的动态破坏特性;

(2)测试了黄铜的J-C模型曲线和真实应力-应变曲线,拟合得到了黄铜的J-C本构模型,黄铜的拟合曲线与实验曲线吻合较好,相对误差小于9.38%。

(3)黄铜(H62)在25℃～570℃范围内,有明显的应变硬化效应,25℃～270℃范围内几乎没有热软化效应,而在570℃～790℃范围内有较大的热软化效应。