目的层预约智能优化电梯群控研究

付丽君，牟晓晨

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

电梯群控技术是一个重要的研究课题，许多先进的群控算法和控制方式都被应用到电梯群控系统中。1997年，迅达电梯公司提出目的层客流管理系统，就是将外呼上下行按钮改为目标层选取，并反馈所派轿厢序号引导乘客乘梯[1]。目前在国内对于目的层预约模式的群控策略研究还处于起步阶段，这种具有新型客流分配模型的电梯群控系统成为新的研究热点和发展方向。1965年，使用隶属关系来表示数据差异的想法被提出，后来演变为模糊控制算法。模糊控制就是对于输入参数进行模糊化，并根据参数映射的模糊规则关系确定输出模糊量，最后将模糊量清晰化得到结果。目前模糊控制研究已经相对成熟，其控制参数的选择以及模糊规则的选取对结果的影响尤为重要[2]。20世纪90年代Dorigo等提出蚁群算法[3]，这是一种仿生算法，算法开始时，蚂蚁选择路径概率相同，并且行动时留下信息素，后来，蚂蚁根据信息素的多少有选择性的对路径进行选择，由于路径长信息素的浓度低，因此形成一种正反馈机制。目前基于蚁群算法的应用非常广泛，它类似于粒子群算法，经常被用于优化参数。

目的层预约型电梯群控方法对于电梯群控算法的要求很高，要实时分析数据预测所需参数值并给出合理的派梯策略[4]。通过对各种先进算法的研究发现，使用蚁群算法优化模糊控制派梯策略理论上可以达到理想的优化结果。建立合理的模糊规则，根据不同交通流的权值分配和模糊规则[5]，得到合适的派梯函数进行优化派梯。本文建立基于目的层预约的电梯群控调度仿真模型，以上行高峰为例使用蚁群算法优化模糊控制算法进而优化派梯策略[6]。同时与未被优化的参数做比较得出结论。

1 电梯群控模型的建立及仿真

1.1 目的层预约型电梯群控调度

目的层预约呼梯系统需要每位乘客输入目的楼层，通过对目的层与起始层的大小判断确定轿厢上下行。由于轿厢到达前已获取了乘客的目的层，对于派梯算法而言，输入参数包括了目的层，可以将起始层和目的层都输入到群控派梯算法中。因此，目的层预约虽然对于乘客操作及判断上多了些步骤，但对降低轿厢拥挤度和乘梯时间都有很大的作用。目的层预约呼叫面板获取呼梯信息，包括乘客序号、呼梯时间、起始层、目的层。从单梯轿厢控制器中获取轿厢位置，轿厢运行方向，轿厢已响应的呼叫。图1是目的层预约型电梯群控的系统框图。

图1 目的层预约电梯群控系统框图

1.2 客流量仿真

为了模拟呼梯情况，运用泊松过程及不同模式下随机抽样法建立客流量仿真模型。

1.2.1 时间信息确定

乘客到达的时间顺序可以近似为一个泊松过程[7]，需要仿真的是下一位乘客到达的时间间隔。连续泊松过程的公式为

(1)

式中：P(t≤T)表示[0,t]，k名乘客乘梯概率；λ表示需要乘梯的人数；T表示时间周期。

则有乘客到达的概率为

Pk>0(t≤T)=1-e-λT

(2)

所以乘客到达时间间隔为

(3)

1.2.2 起始层与目标层确定

电梯运行大致分为如下几种交通流：

(1)上行高峰：乘客大部分从基站出发；

(2)下行高峰：乘客大部分到基站；

(3)层间交流：上下行相对平衡状态。

确定起始层与起始-目的矩阵，根据起始层与目的层不相等，确定目标层。首先产生范围为[0,1]的随机数，设置每层的概率范围，以此确定起始层。再定义起始-目的矩阵OD。最后将j=起始层，i=j的元素去除，产生范围为[0,1]的随机数，设置除起始层外，所有层概率相同。

(4)

式中，元素odij(i,j=1,2,…,N)表示从i层到j层的客流量。

2 蚁群算法优化模糊控制模型

在算法设计过程中，加入了对交通模式的识别，不同于其他算法，本设计将全局运算的模糊控制算法分为两个局部运算的算法，首先通过建立贝叶斯模型分析采得数据来识别交通模式，再使用蚁群算法优化参数，最后使用模糊控制算法优化派梯方案。

2.1 交通模式识别

实际中的电梯交通流是以时间与总客流量为轴，确定高峰，以时间与上下行客流为轴确定模式。以此对上行高峰，下行高峰，层间交流三种交通模式进行识别。样本空间为

U={w1,w2,w3}

(5)

式中:w1为上高峰模式；w2为下高峰模式；w3为层间交流模式。

预先确定各种模式的概率P(wi)以及特征值X。

(6)

X={x1，x2，x3}

(7)

式中：x1为5min内总客流量；x2为5min内下行至门厅的客流量；x3为5min内从门厅上行的客流量。

将一昼夜时间以5min等分为288份，根据不同交通模式下的条件概率密度函数，建立贝叶斯鉴别函数P(wi|x)[8]。

P(wi|x)=max{P(wi|x)}，(i=1,2,3)

(8)

x∈wi且最终根据离散时间-模式函数确定电梯运行模式。

2.2 模糊控制派梯策略

定义多目标评价函数，根据输出变量选择输入变量并确定对应模糊规则。

Si=W1SAWT+W2SCC+W3SRPC

(9)

式中：W1、W2、W3代表权重系数；Si为评价函数值；SAWT为平均侯梯时间隶属度函数；SCC为轿厢拥挤度隶属度函数；SRPC为能源消耗隶属度函数。

乘客等待时间(THCW)：

Ti HCW=Tmove+Tstop

(10)

式中，Tmove表示电梯运行时间；Tstop表示电梯停靠时间。

如图2a所示，将变量模糊化小于10秒为非常快(VFTHCW)；10秒到20秒为快(FTHCW)；20秒到35秒为一般(MTHCW)；35秒以上为慢(STHCW)。

轿厢剩余容量(CV)：

(11)

如图2b所示，将变量模糊化20%以下为舒适(SCV)，40%到65%之间为一般(MCV)，超过65%为拥挤(CCV)。

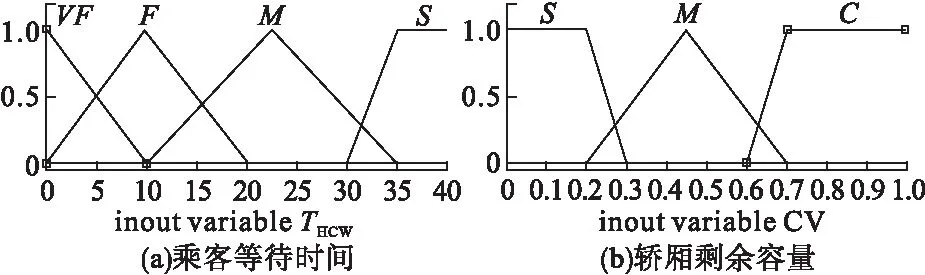
图2 乘客等待时间和轿厢剩余容量模糊隶属函数

召唤集中程度(GD)是起始层位置与电梯需要响应呼叫的集中程度，可以反应轿厢的能耗。

(12)

式中，h为楼层高度；d为楼层与停靠楼层的高度差。

如图3a所示，将变量模糊化20%以下为能耗小(SGD)，40%到65%之间能耗适中(MGD)，超过65%为能耗大(LGD)。

轿厢总利用率(UR)：响应呼叫的总概率。

(13)

式中：NF为总楼层数；CV0为轿厢额定容量；n为同方向召唤次数；NFi为第i层楼层与起始楼层的差值；NPi为第i层的人数。

如图3b所示，将变量模糊化小于20%为低利用率(LUR)，大于60%为高利用率(HUR)，介于二者之间的为一般(MUR)。

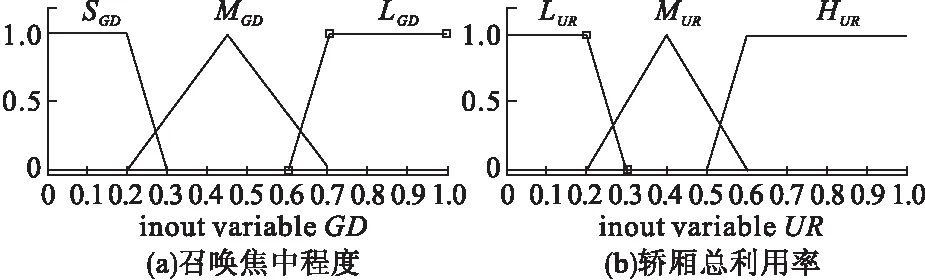
图3 召唤集中程度和轿厢总利用率模糊隶属函数

根据输入变量与输出变量建立模糊控制规则[9]：

(1)等待时间与平均侯梯时间成正比；

(2)轿厢剩余容量与轿厢拥挤度成反比；

(3)召唤集中度，平均侯梯时间越短，能源消耗越低，但同时轿厢也越拥挤；

(4)轿厢总利用率与能耗成反比。

2.3 蚁群算法优化模糊控制

蚁群算法是一种搜索最短路径的算法，收敛快，将模糊控制算法得到的数据进一步优化，得到最合适的派梯方案[10]。

(1)基于多目标评价函数的结果建立蚁群算法输入矩阵

(14)

式中：D为多目标评价函数结果，输入矩阵每个元素都是经过模糊控制算法计算得到的实时数据；k为轿厢编号；i为电梯层数。

(2)定义最大迭代次数Nmax，蚂蚁数量m，以轿厢位置为初始位置并初始化信息量τ(k,i)=1，Δτ(k,i)=0。

(3)蚂蚁根据状态转移概率pk(k,i)选择下一目的地

(15)

式中：τ(k,i)为蚂蚁k到楼层i信息素量；α为信息素挥发因子；β为期望值挥发因子；allowed为蚂蚁k选择楼层。

(4)使用禁忌搜索方法，即蚂蚁经过的楼层被加入禁忌表，直到所有楼层都遍历，将m只蚂蚁中所得的最小值路径保存。

(5)更新信息素

(16)

式中：1-ρ为信息素残留因子；Q为信息强度；Ln为第n只蚂蚁走的总长度。

(6)所有蚂蚁都到终点标志着一次迭代完成，将禁忌表重置，迭代次数+1，重复迭代过程直到达到最大迭代次数Nmax。

3 仿真结果与分析

以6部20层的办公楼电梯群为仿真对象，分别对客流量及算法进行仿真。

3.1 客流量仿真

对三种模式5分钟内客流量进行仿真，设置到达率分别为0.65、0.85、0.15，仿真结果见表1。结果显示，与输入参数一致，符合各自模式客流特点。

表1 5分钟内的客流量模拟结果 %

3.2 算法仿真

设置电梯最大速度3m/s，加速度1m/s2，楼层高度4m，电梯额定容量15人，开关门时间、每位乘客进出时间1s。以上高峰为例分配权重系数如下：

W1=0.7,W2=0.2,W3=0.1,ρ=0.2,

α=1,β=3,Q=100,Nmax=50

优化前曲线如图4a，优化后曲线如图4b。从纵坐标可以看出，优化后效率提升25%，由此证明算法优化确实有效。

4 结论

使用目的层预约呼梯，打破传统呼梯方式，减少系统响应时间。结合蚁群算法优化模糊控制算法，得出多目标评价函数值，做出最合适的派梯选择。仿真结果显示算法收敛快，且效率提升了约25%，该方法实际可操作性强，能够应用于实际电梯群运行，有一定的实际应用价值。