影像信息驱动的三角网格模型优化方法

张春森，张萌萌，郭丙轩

1. 西安科技大学测绘科学与技术学院，陕西 西安 710054； 2. 武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430079

基于影像的多视图三维重建流程包括：采用SFM技术恢复摄像机的运动和场景的稀疏结构，采用多视图立体技术将SFM产生的稀疏点云密集化以及通过密集的点云生成表面模型并产生对应的纹理。上述步骤中的每个环节都将影响最终生成的三维模型质量。对于影像匹配的研究，计算机视觉与摄影测量领域有大量的研究成果，但是对于密集匹配后三维模型重建的研究则相对较少。目前由点云数据生成三维模型的成熟算法，多是针对由三维扫描仪获取的点云数据。而与数据均匀、致密和精确的三维扫描仪获取的点云数据相比，采取摄影测量计算机视觉方法获取的点云数据，由于存在疏密程度不均匀，不够致密和精确，因此在应用已有表面重建算法时，无论是采用图割 (graph-cut)法或者是泊松(Poisson)方法产生的三角网格(mesh)通常都存在有孔洞、凹坑、凸起等现象，导致三维模型与真实场景在几何一致性上存在差异。因此，如何构造完整的表面模型使构建的模型为流形表面仍然是一个独立的、具有挑战性的研究方向。迄今为止，已有许多国内外学者对三角网格优化进行了研究。其中，文献[1—2]通过在网中补充新的观测量来改善已有地面三角网精度。文献[3]利用控制点构建的初始Delaunay三角网，采用三角面面积和角度双重约束来优化控制点三角网。文献[4]首先同时使用最小内角最大化方法和最小权方法进行优化，然后，在完成一对相邻三角形的优化后，判断它们是否为狭长三角形，进而删除狭长三角形，达到优化三角网格的目的。文献[5] 提出一种基于局部-全局方法的平面三角网格优化算法。在局部阶段利用自定义的最相似规则，为网格中的每一个三角形单元求取与之最相似的正三角形，得到一组目标仿射变换函数。在全局阶段采用尽可能刚性方法，利用最小二乘法求取一组满足最小变形能量函数的最优解，使得最终生成的网格由尽可能相似于正三角形的三角形构成。文献[6]先用给定一些顶点集重构多边形，生成多边形表面，运用稳健性估计进行三角网细分，利用新点集替换掉原始顶点集，生成多边形表面模型，再利用最大曲率局部估计，增加更多点来更精确地表示物方表面，并利用平滑性转化参数将原始复杂模型进行粗略表达。

影像数据作为影像三维重建的原始数据，含有丰富的信息，利用影像信息进行三角网格(Mesh)模型优化时，优化信息源易获取，充分利用影像信息进行优化，可得到较好的优化效果。文献[7—8]采用光学多视立体原理进行三角网格优化，对由投影影像组成的影像数据矩阵进行分解，得到估计表面法向量。利用估计法向量与物方点对像点梯度信息，计算得到一个二维位移图，根据位移图，在法向量上移动物方三角网格上的物方顶点，实现三角网格优化。文献[9]对散乱点云进行特征提取，然后将特征信息加入至点云数据中，处理得到初始网格模型，对平面法向量进行粗估计，进行三角网粗化同时更新阈值，通过迭代、三角网信息分割、再进行表面平滑处理，最终得到优化后的网格模型。上述方法基本都是基于物方优化三角网，即对原始三角网格进行调整，使得最终优化后的模型三角形形状更加规则，三角网格模型与真实地表曲面模型误差最小。文献[7—8] 中，虽然也是基于影像信息进行优化，但是对二维三角网的优化，获取影像时光源信息也必须只来源于单光源，利用此方法实现三角网优化时，对客观条件有着很高的要求。显然，此优化方法不适用于测绘领域进行三维重建时的三角网格优化，但其是基于影像信息，因此相关原理有一定的可借鉴性。

文献 [24—25]采用首先输入影像数据，再进行空三解算和密集匹配处理，然后对密集的点云进行构网得到三角网格模型的方法，由于未对网进行优化处理，因此模型的效果不好。文献 [26]提出的PMVS法，是通过能量函数最小化优化三角网格，平滑项采用的是Laplacian平滑，数据项也是通过影像信息优化，与本文优化方法不同。

本文以影像信息为驱动，利用影像信息和投影几何原理，将影像间相关系数对物方点求导得到的梯度变化值，根据重心化坐标对三角面三个顶点的贡献，调整物方三角面顶点，通过最小化能量函数，达到优化物方三角面，进而得到优化后的网格模型。

1 本文网格模型优化方法

本文采用Delaunay三角网作为网格模型优化的初值，利用投影几何原理，采用梯度下降法，通过影像相关系数对物方点坐标X、Y、Z分别求导，得到物方点的梯度变化值。根据重心化坐标加权得到物方顶点的梯度变化值，利用最小化匹配代价，驱动三角网顶点在法向量方向上移动，使能量函数达到最小，实现三角网格优化。

1.1 构建三角网

三维重建需将离散的三维点云转换成连续的三维表面。因Delaunay三角网具有强大的可操作性，如可对顶点、边和三角面实现添加、复制、移动或者删除操作，有助于三角形的简化和优化处理，故本文通过构建Delaunay三角网格[15-16]实现三维重建，将其作为后期三角网格模型优化的初值。

1.1.1 简化和细分三角网

由于初始三角网格模型多存在三角网过于密集，点、边不满足流形性质，以及存在孤岛、小面积三角面、孔洞以及狭长三角面等现象，需对其进行简化处理，以得到满足大小的简化三角网格模型[17]。同时为确保三角网在每张影像上投影时，投影的网格不大于所给定的像素个数，需对简化后的三角网格采用一剖四的方法进行细分，如图1所示。选择并连接原始三角网中所有三角面各边中点，得到细分后的三角网格。

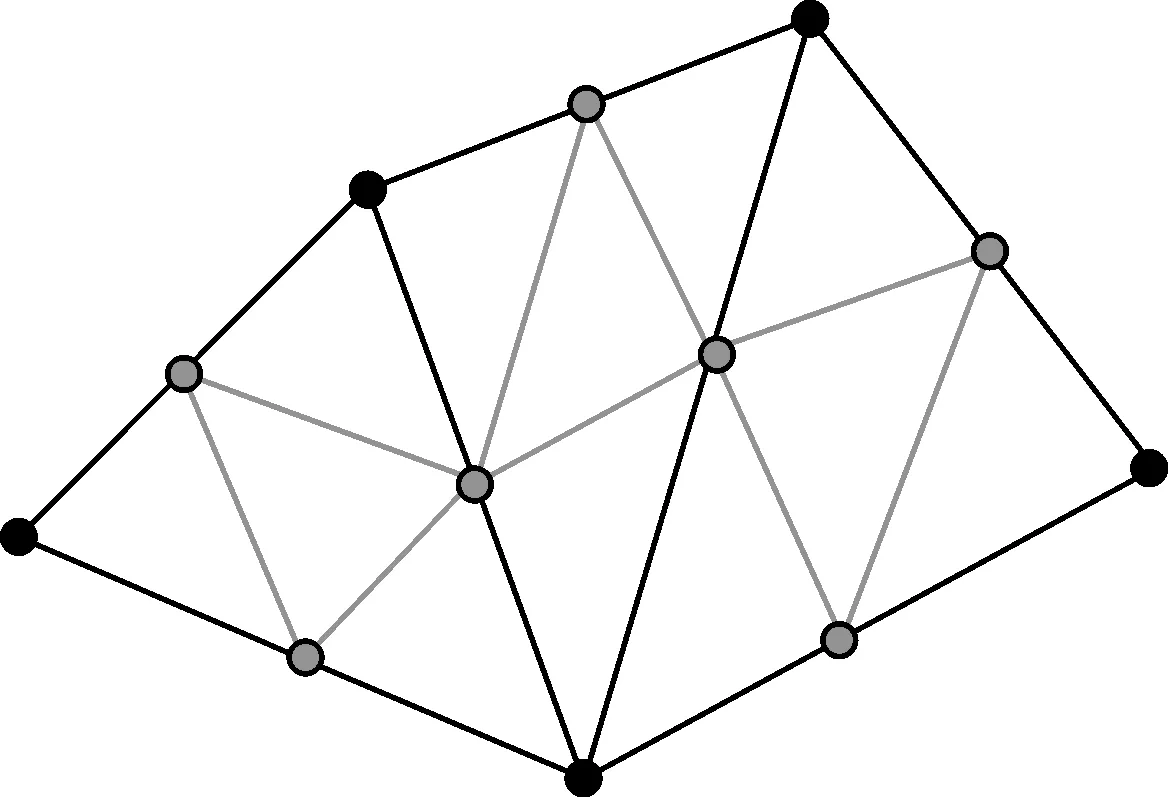
图1 一剖四方法说明Fig.1 One subdivide to four method illustration

1.1.2 生成流形三角网

可以被摊成一片连续的2D平面，称为流形几何(2-manifold geometry)[18]，如图2所示。三角网格中，包含非流形边(non-manifold edge)(一条边连到3条以上的面)和非流形顶点(non-manifold vertex)(两个以上的面分享一个点却没有分享任何线，或造成非流形边的点)的三角面，称为非流形三角面，需对其进行处理，使构建的模型为流形表面。图3中深灰色标注的顶点为非流形顶点，深灰色标注的线为非流形边。通过对非流形顶点进行复制，然后对复制的顶点移动一个微小偏移量，得到一个新的顶点，从而得到满足流形性质的流形三角网网格。处理过程如图4所示。

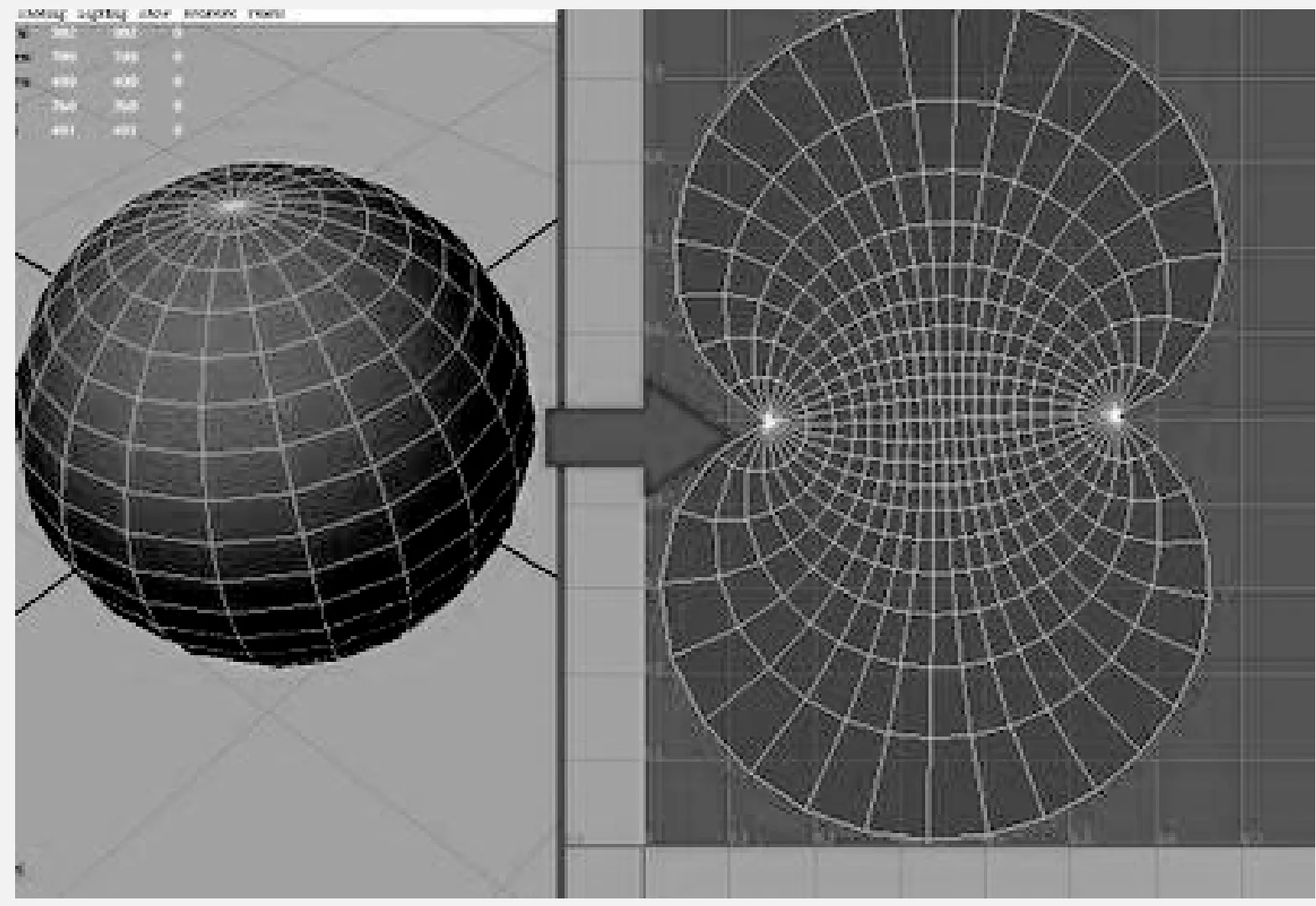
图2 流形几何Fig.2 Manifold geometry

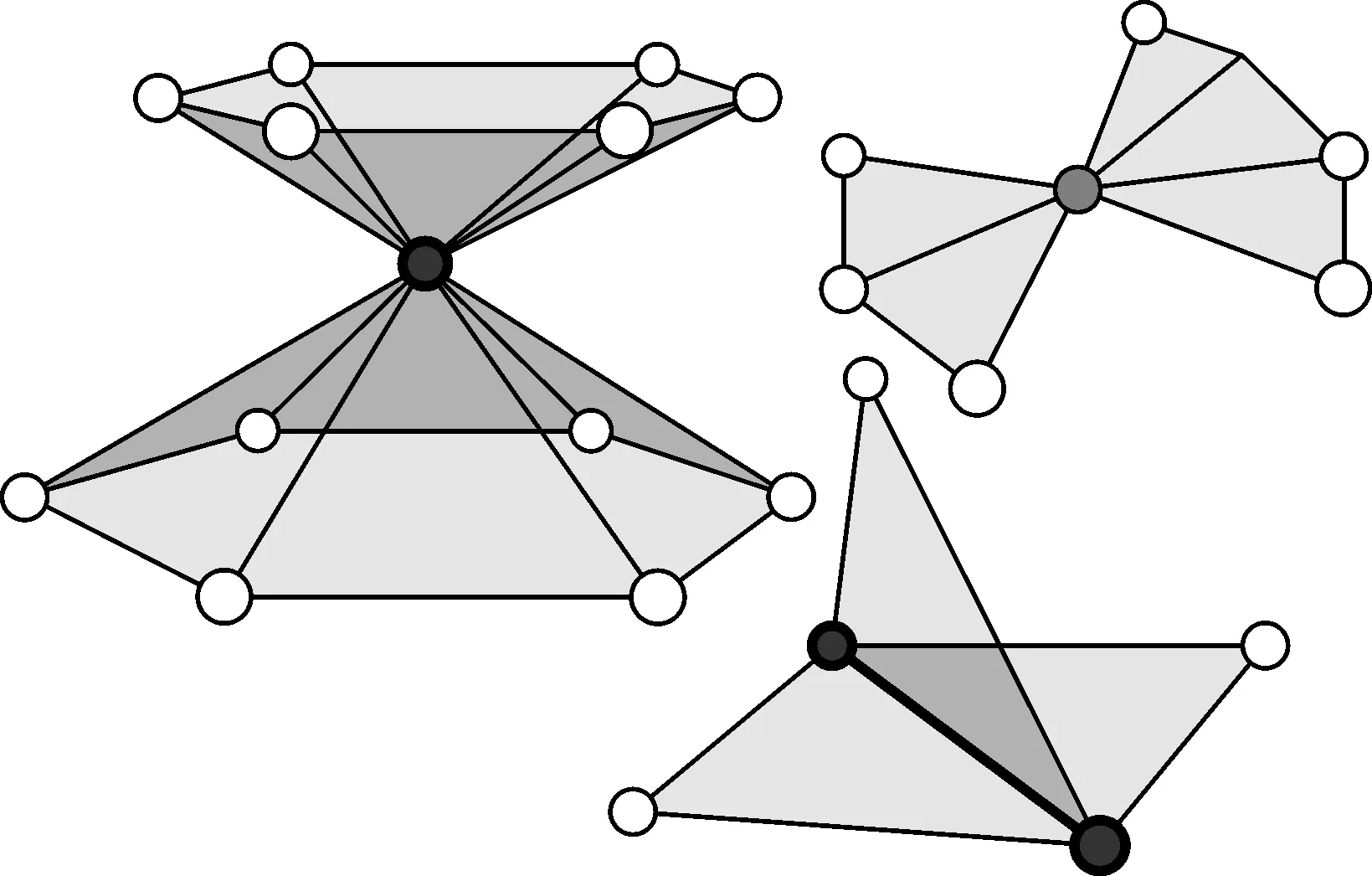
图3 非流形边和非流形顶点Fig.3 Non-manifold edges and non-manifold vertices

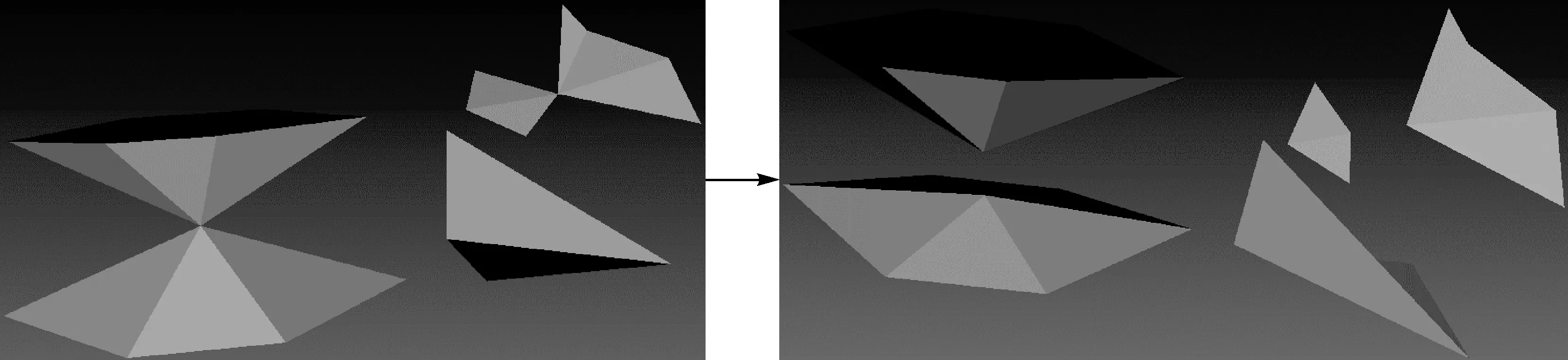
图4 非流形几何处理为流形几何Fig.4 Transform non-manifold geometry into manifold geometry

1.2 优化三角网

1.2.1 求解物方顶点梯度变化值

为实现影像信息驱动的三角网格优化，根据影像信息，将影像间归一化互相关系数NCC[19]对物方点进行求导，得到一个物方点的梯度变化值。将三角面内所有物方点的梯度变化值，根据其重心坐标对三角面顶点各贡献一个权值，在法向量方向上调节物方顶点，以达到优化的目的[20-21]，顶点优化处理过程如图5所示。

(1) 求解像点x梯度变化值gB。任一物方点X在影像对(A,AB)上对应像点x处的能量

Edata(X)=h(IA,IAB)(x)=1-NCC

(1)

对物方点X求导，计算得到物方点梯度变化值gB。

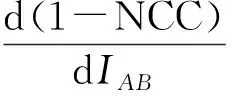
NCC=

(2)

式中

(3)

(4)

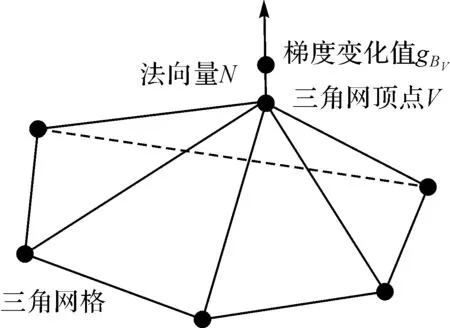
图5 三角网顶点优化处理过程Fig.5 Triangulation vertex optimization process

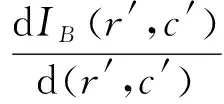
(5)

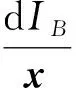
(6)

④ 求解像点对其对应物方点梯度变化值gB。

(7)

(2) 求解像方顶点v梯度变化值gBv。设v1、v2、…、vk是向量空间I中的一个单形(三角形或四面体)的顶点，如果I中某点x满足：(φ1+…+φk)x=φ1v1+…+φkvk，则(φ1,φ2,…,φk)为x关于顶点v1、v2、…、vk的重心坐标。

物方三角网顶点V投影至影像上对应影像三角面的像方顶点v，x为此影像三角面内的像点，像点x重心坐标为(φ1(x),φ2(x),…,φk(x))，因此，对顶点v的重心坐标为φ(x)，则对像方顶点v的梯度变化值为

gBv=φ(x)gB

(8)

(3) 求解物方顶点V梯度变化值gBV。物方三角网顶点V投影至影像上对应的影像三角网顶点为像方顶点v。同一影像三角面内，所有像点对此像方顶点v贡献多个梯度变化值。同时，不同影像三角面内像点也对此像方顶点v贡献多个梯度变化值。因此，将物方顶点V对应的像方顶点v的梯度变化值整体相加，得到物方顶点V的梯度变化值gBV。

(9)

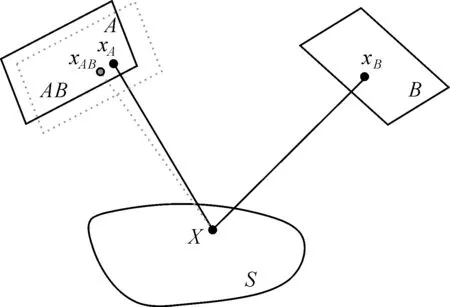
图6 影像重投影关系Fig.6 The relationship of image re-projection

1.2.2 构建能量函数

利用能量函数驱动初始三角面优化。能量函数由两部分组成：数据项Edata和平滑项Esmooth

E(S)=Edata(S)+λEsmooth(S)

(10)

能量函数中的数据项Edata为

(11)

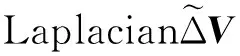
(12)

式中，w1=0.18和w2=0.02分别表示平滑项中柔性权值和刚性权值。

能量函数最小化[23]时，三角网格为最优，其对应梯度值为0，即

(13)

2 试验结果与精度分析

2.1 三角网格优化效果比较

对武汉大学信息学部3S广场，采用Panasonic DMC-GF3相机拍摄，相机焦距为14 mm，影像大小为4000×3000像素，拍摄得到9张试验用影像数据(如图7)，图8为对广场影像优化前后三角网格效果对比，图9为影像数据进行密集匹配处理后得到的三维点云，图10为点云重构三角网格得到的初始三角网格模型，图11为优化后的三角网格模型，图12为映射纹理信息后得到最终的三维模型，图13和图14展示了MVE(multi-view environment)法得到的三角网格模型和三维模型。

图7 2张(共9张)3S广场影像Fig.7 Two of 9 images of 3S square

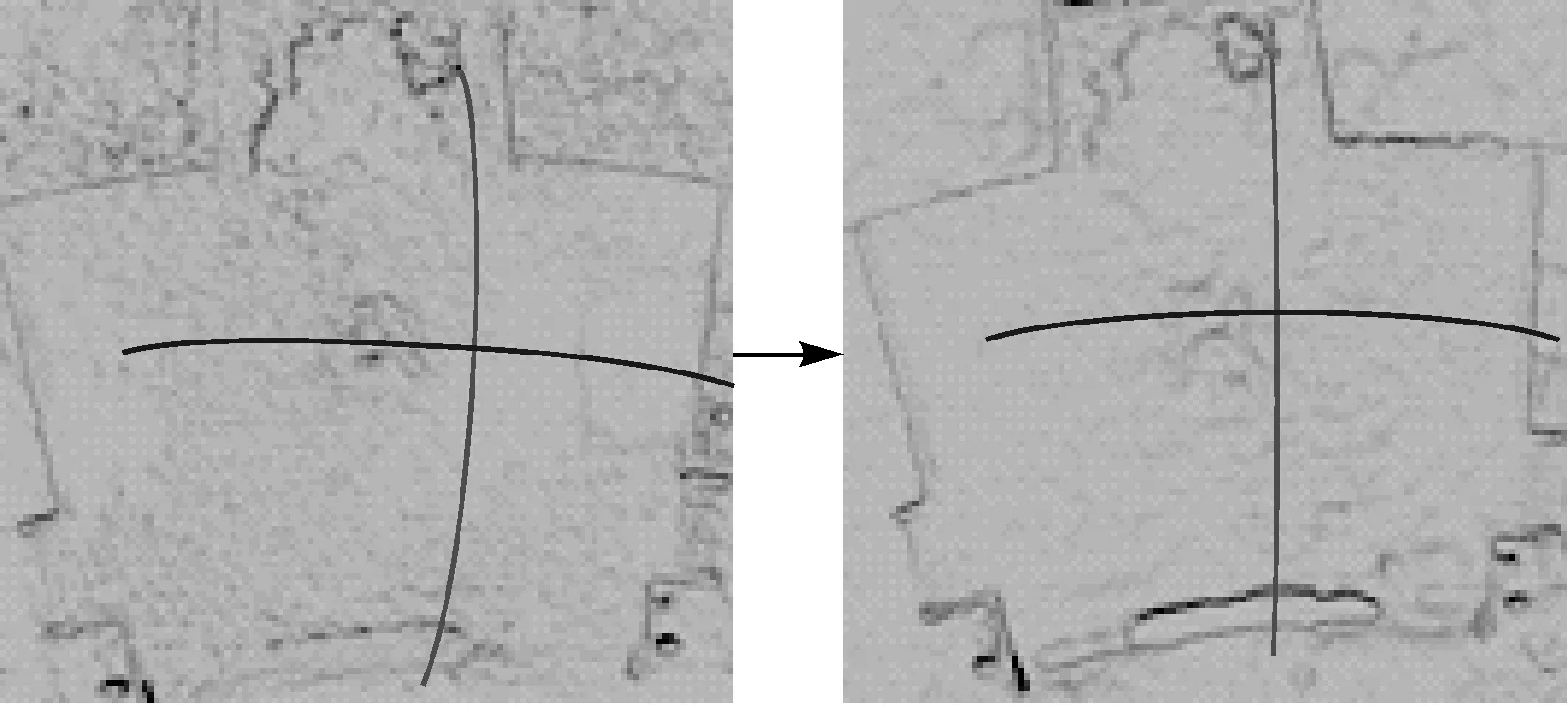
图8 广场中心优化前后三角网格对比Fig.8 Square center before and after refinement contrast

图9 本文方法生成的三维点云Fig.9 3D point cloud generated by the proposed method

图10 本文方法生成的初始三角网格模型Fig.10 Initial 3D mesh generated by the proposed method

图11 本文方法生成的优化三角网格模型Fig.11 Refined 3D mesh generated by the proposed method

图12 本文方法生成的三维模型Fig.12 3D model generated by the proposed method

图13 MVE法生成的三角网格模型Fig.13 3D mesh generated by MVE

图14 MVE法生成的三维模型Fig.14 3D model generated by MVE

2.2 三角网格优化精度分析

从图8中可以看出优化前后三角网格的表面纹理及粗糙度发生了明显的变化。对比图11和图13，以及图12和图14发现：本文方法的优化效果好于MVE方法。从图中可以看到，MVE生成的三角网格模型及三维模型中存在孔洞，以及模型不完整情况。由此说明，本文方法可更详细和精确地建立三维模型。三角网格模型优化前后三角网中顶点和三角面个数发生变化统计如表1所示。由于优化时不仅是移动了顶点位置，同时也对三角网格模型中的错误和冗余的顶点及三角面进行了处理。从表中发现：优化前后顶点个数及三角面个数的同时减少，说明采用本文方法起到了优化三角格网的目的。但在执行时间上，本文方法执行时间长于MVE方法，故后续研究需要更进一步提高优化处理速度，降低执行时间。

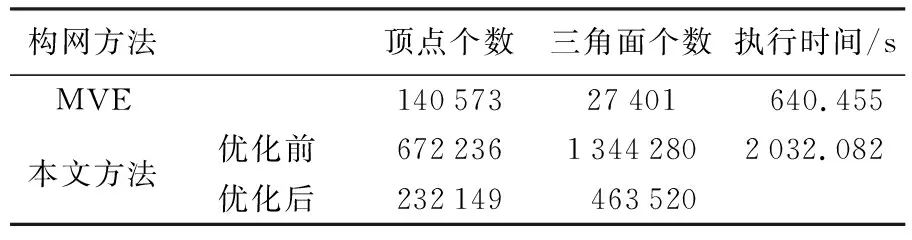
表1 三角网格优化前后顶点和三角面个数对比

表面粗糙度表示的是点云拟合到平面的均方根误差，可以用来反映三角网格模型精度及效果，表2为友谊广场中心的3S雕塑及其左侧台阶的表面粗糙度值统计。从表中可以看出，本文方法生成的三角网格模型的表面粗糙度值均比MVE法生成的三角网格模型的表面粗糙度小。MVE物方平面粗糙度值大的原因是未对三角网顶点位置进行优化处理。

2.3 与其他三角网格优化算法比较

利用本文方法对图15所示标准测试影像数据喷泉和入口进行网格优化，并与ST4法、MVE法、PMVS法优化结果进行对比。对比结果如图16与图17所示，图18和图19为对喷泉和入口重建的三维模型显示。

从图16—图19可以看出，本文的优化方法可有效保证拓扑信息和边界信息精确地重建。由于所给算法通过平滑项对物体表面的约束，使弱纹理区或模糊区域也可较完整地修复。然而，该算法是基于影像信息不断迭代更新，最终实现三角网格模型最优，因此，与上述两种方法相比，当影像数量过多时，优化速度较慢，如表1中，本文方法对9张影像构成的三角网格进行优化处理，执行时间为MVE 方法的3倍多。为了提高优化速率，需要更高的计算机硬件配置。

表2 表面粗糙度分析

图15 3张(共11张)喷泉影像和3张(共10张)入口影像Fig.15 Three of 11 images of fountain-P11 and three of 10 images of entry-10

图16 ST4法、MVE法和本文方法生成的优化三角网格模型Fig.16 Refined 3D mesh model of fountain-P11 generated by ST4，MVE and the proposed method

图17 PMVS法、MVE法和本文方法生成的优化三角网格模型Fig.17 Refined 3D mesh model of entry-10 generated by PMVS，MVE and the proposed method

图18 本文方法生成的喷泉三维模型Fig.18 3D model of fountain-P11 generated by the proposed method

图19 本文方法生成的入口三维模型Fig.19 3D model entry-10 generated by the proposed method

3 结 论

本文结合摄影测量与计算机视觉相关理论，给出了基于影像数据实现三维重建中三角网格优化的一种方法。利用影像同名特征点间相关系数、影像梯度信息和投影几何信息3部分组成能量函数数据项，以拉普拉斯平滑作为平滑项(正则项)，驱动物方三角网顶点在法向量方向上进行移动，最小化匹配代价，当能量函数最小时，三角网物方顶点位置为最优，实现网格优化，使三角网格与实际表面误差最小，进而提高三维重建结果的精度。试验结果表明，本文方法能较好地保持模型的视觉特征，具有一定的实际应用价值。由于该方法是对每个三角面物方点计算梯度变化值，进而加权给物方三角面顶点，因此当数据量较大时，优化速度较慢。同时，试验发现在一些高程变化显著的区域，因梯度下降法原理中步长设置的约束，使得在此区域优化效果不是很好。

下一步的研究设想是：①在整个计算过程中，对多次重复计算过程进行优化，对其存储，减少其计算过程，如计算影像间归一化相关系数中的相关变量；②根据影像间交会角大小，计算每个物方三角面中物方点梯度变化值，给予一个权值，使得在最优交会角范围内的物方点梯度变化值最优，以此来达到优化物方三角网格的目的。当然，在给出优化算法的同时，如何缩短优化时间也是后续要研究的内容。