轻小型喷灌机桁架结构力学性能分析与优化设计
曹炜林,朱德兰,葛茂生,李 丹
(西北农林科技大学 旱区农业水土工程教育部重点实验室,陕西 杨凌 712100)
中心支轴式与平移式喷灌机具有自动化程度高、灌水均匀等优点且适合我国耕地分布情况,具有广阔的应用前景,迄今为止是应用最为广泛的喷灌机型[1-3]。其整体跨长往往可达数百米,对地形要求较高,主要适用于大型平原农场灌溉,在美国、澳大利亚等国以及我国黑龙江、内蒙古等地均有广泛应用[4,5]。但由于我国陕西、甘肃等西北地区多为小型农田种植方式,地块面积较小、地域障碍较多,传统的大型喷灌机没有施展空间[6,7];且灌溉方式以大水漫灌为主,使得水资源浪费严重,灌溉效率十分低下[8]。在实际应用过程中,上述喷灌机仍存在用料冗余及结构不稳定现象,内蒙古等地出现的部分喷灌机倒塌状况即可能与之有关,为保证喷灌机桁架结构的安全可靠,其力学性能和合理性有待进一步研究。综上所述,适用于西北地区地形的节水灌溉设备亟待出现。本文所研究的轻小型移动式喷灌机是仿照传统大型平移式和中心支轴式喷灌机而造,具有移动方便,造价成本相对较低,灌溉效率高等一系列优点[9,10]。
上世纪末,李鸿明利用力法对中心支轴式喷灌机进行桁架计算与设计,王泰恩分析了大型喷灌机桁架的内力特点和计算方法[12],王荣根据大型喷灌机机架的受力特点对桁架设计提供需遵循的基本原则和设计方法[13],葛茂生根据经验设计出轻小型移动式喷灌机,并对其进行了结构优化[14]。前人分别对中心支轴式喷灌机机架的设计机理与验算进行了详细探索,多采用经验设计及手动计算方法,但对于喷灌机的合理结构尺寸和形式探讨较少,也较少涉及风荷载对于桁架结构的影响。针对上述问题,为进一步了解喷灌机桁架结构受力特性,使得喷灌机桁架结构朝轻小型和经济性发展,本文在平移式和中心支轴式喷灌机的单跨结构的基础上,设计一款轻小型移动式喷灌机桁架结构;对其在自重、水重及风荷载作用下的力学性能进行探讨;以整体结构质量最轻为目标函数,各杆件截面尺寸为设计变量,最大应力和最大位移为约束条件,利用ANSYS零阶算法对喷灌机桁架结构进行尺寸优化,并分析桁架结构尺寸的变化对于喷灌机结构稳定性与经济性的影响。以期为今后轻小型喷灌机桁架结构力学性能分析和结构优化设计提供参考。
1 轻小型喷灌机桁架结构设计
本文所研究的轻小型移动式喷灌机桁架结构是参考传统大型喷灌机桁架结构而构建,其主要构件包括输水管道、腹杆支撑、拉筋以及端悬臂,如图1所示。其中,输水管道为圆形中空钢管,负责输送水、承受外界与自身荷载所施加的轴向压力与弯矩;腹杆支撑为型钢,呈“V”型结构形式布置于机架中,负责承担压力与连接上下弦杆(输水管与下方拉筋),使荷载均匀分布;拉筋为圆形钢筋,负责承受整体结构所带来的拉力。三者共同组成空间桁架结构,为整体喷灌机的稳定性提供支撑。为延长喷灌机喷洒面积,两端外接悬臂,亦为圆形中空钢管,主要负责输送水至两端。结构所承受荷载主要是自重、输水管中水荷载与风荷载等。

图1 喷灌机结构简图
针对西北地区常见耕地尺寸,设计桁架结构的整体跨长为50 m,中间跨度为38 m,每边悬臂长6 m。参考文献[11],上弦根据合理拱轴线等一般采用二次抛物线型,下弦采用鱼腹型,其节点也在某二次抛物线上。其拱轴方程根据结构力学[15]推荐为:
(1)
式中:f为矢高;L为中间跨长。
参考文献[11-13],矢高过大会使重心过高影响桁架稳定性,矢高过小会增加拉筋拉力影响桁架强度,因此选择矢高时使重心落在两支座连线上为宜。根据国内外同类样机参数:矢高为0.4~0.8 m,并参考SYP-400型水动时针式喷灌机、维蒙特圆形喷灌机等的桁架数据。如图1所示,此处中间悬架张角为85°,上弦矢高f1确定为0.8 m,下弦矢高f确定为1.79 m。根据以上数据确定出喷灌机具体结构。
2 模型构建与力学性能分析
该轻小型喷灌机桁架所有组件均采用Q235钢,密度为7 850 kg/m3。在ANSYS软件中输水管与型钢均为拉压构件,应用BEAM188单元,拉筋在实际应用中承受拉力,应用LINK10单元。喷灌机桁架结构与两端支座相对固定,视为施加全约束。为方便以后修改结构类似、尺寸不同的分析模型,避免大量重复工作,有限元建模求解过程均采用APDL语言。
2.1 喷灌机有限元模型构建
喷灌机各杆件的截面特性如表1所示。

表1 各杆件截面特性
喷灌机承受荷载主要为自重、水重及风荷载。该桁架承受的主要荷载为自重和水重,若将其简化为平面结构,可发现其结构左右对称、荷载对称,且荷载都是均匀分布。
对其施加相应荷载,分为3种工况:结构自重;结构自重+水重;结构自重+水重+风荷载。此处为使求解结果精确,水重作为均布荷载换算成输水管密度以重力加速度形式施加,换算后输水管密度为2.030 75 万kg/m3。
风荷载属于侧向水平荷载,根据标准风压公式:
(2)
式中:Wp为风压,kN/m;v为风速。根据《建筑结构荷载规范》[16],陕西西安地区五十年一遇基本风压值为0.35 kN/m。
该模型经网格划分后共124个节点,50个单元。其中,1~11号杆件为供水管单元,12、13号杆件为悬臂单元,14~25号杆件为拉筋单元,26~50号杆件为角钢单元。喷灌机有限元模型如图2所示。
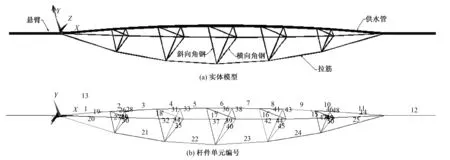
图2 喷灌机有限元实体模型及杆件单元编号
2.2 求解结果与力学性能分析
如表2所示,可得到有限元模型分别施加相应荷载的求解结果,3种工况下桁架结构的受力特性与变形情况见表2。

表2 3种工况下结构受力与变形情况
由表2可看出桁架结构分别在3种工况下的位移与受力情况。3种工况下结构最大位移即为中点位移,较大位移为悬臂两端位移,且最大轴力均发生在供水管5号杆件上。工况二与工况三支座反力数值相近,可见风荷载对于支座反力大小并无影响。杆件最大应力发生在5号杆件上,可见风荷载对于最大应力的影响较小。工况一与工况二最大弯矩基本相同,发生在17号杆件,工况三的最大弯矩发生在12号杆件,可见施加风荷载后对于结构的弯矩变化影响明显。
如图3所示,是喷灌机桁架架构在承受自重+水重+风荷载下的应力应变云图与结构位移图。为方便观察桁架结构的变形情况,增加了整体位移的放大倍数。观测方向为喷灌机桁架结构的主视图方向。图3中MX为桁架结构变形后拉筋中部的最大位移情况,它是因自重+水重荷载造成了整体桁架结构向下位移,且由于风荷载作用使桁架整体倾斜,使得一边拉筋向下位移较大,故拉筋中间部分是桁架结构的最大位移处,其变化数值为5.8 cm。由于两边有支座固定,故桁架结构整体变形情况是中间变形最大再依次向两边递减。如图悬臂部分也有较大变形,是由于其长度较长,加之自重和水重的影响,两端悬臂刚度变化较为明显。桁架结构各杆件的变形情况均符合实际情形。

图3 喷灌机结构应力应变云图与结构位移图
由ANSYS可输出各杆件轴力数值,根据各杆件的轴力大小能够了解不同杆件类型的受力情况,观察其中最大拉(压)力所属杆件,可便于后续的截面验算。供水管均受压力,其中5号杆件承受最大压力;拉筋均受拉力,16、17号杆件承受最大拉力;横向角钢仅承受压力,最大受力为45号杆件;斜向角钢既承受拉力也承受压力,最大拉力为26号杆件,最大压力为28号杆件。
对于工况三下施加了自重、水重与风荷载的桁架结构进行截面验算,检验其是否满足刚度、强度与稳定性的要求。根据许用应力公式[σ]=σn/n,查表可知Q235钢的应力值为215 MPa,此处安全系数取较高数值为2.5,可得许用应力为86 MPa。桁架杆件的刚度用容许长细比来衡量[17],查得受压杆件的容许长细比为200。具体验算结果如表3所示。

表3 工况三下桁架各杆件截面验算
根据验算结果可以发现,各个杆件强度、刚度稳定性验算值均满足要求并远小于许用应力及容许长细比,即杆件尺寸存在很大冗余量,材料未得到充分的利用,故有必要进行尺寸优化分析以保证结构的经济性。
3 喷灌机桁架优化设计分析
3.1 建立优化模型
喷灌机桁架结构模型经验算后发现在满足刚度、强度、稳定性的基础上杆件用料有较大冗余,因此本研究以整体结构质量最轻为优化目标对桁架结构进行优化设计,在满足桁架结构中最大应力和最大位移要求的条件下使成本最小,即使整体桁架结构质量最轻[18]。采用ANSYS自带零阶方法中的子问题法进行优化分析。零阶方法通过对目标函数逼近或对目标函数加罚函数的方法将约束的优化问题转换为非约束的优化问题,是在一定次数的抽样基础上,拟合设计变量、状态变量和目标函数的响应函数,从而寻求最优解[19,20]。优化设计分析过程利用APDL语言实现。
(1)建立数学模型。以整个桁架结构质量最轻为目标函数;以杆截面积和节点坐标分别作为尺寸设计变量和形状设计变量;以杆件强度、桁架变形量和稳定性为约束条件构建优化模型如下。
尺寸设计变量:
X=[x1,x2,…,xn]T
(3)
A=[A1,A2,…,An]T
(4)
目标函数:
(5)
约束条件:
σi≤[σ] (i=1,2,…,n)
(6)
δi≤[δ] (i=1,2,…,n)
(7)
(8)
式中:X为设计变量;xi为各尺寸变量;n为设计变量数;xn为Am的函数;W为杆系结构重量;ρi为各杆密度;Ai为各杆截面;Li为各杆长度;σi为各杆应力;[σ]为许用应力;δi为各节点位移;[δ]为节点许用位移;Mi为侧向弯矩。
(2)确定尺寸优化变量。为使喷灌机桁架结构达到轻小型的目的,同时满足强度、刚度的要求,根据市场现有杆件尺寸标准,给出相应9个设计变量和状态变量的取值范围,如表4所示。

表4 尺寸优化优化变量列表
3.2 优化结果分析
列出优化模型所选优化变量及优化结果,列出优化模型的目标函数及设计变量的优化过程曲线。讨论优化结果是否达到预期目的。对优化模型采取零阶方法,进行30次优化循环。实际优化序列次数为126次,其中有效序列为32次,分别列出各杆件横截面积随有效优化循环次数的变化曲线。优化前后各杆件尺寸与结构总质量变化情况如表5所示。

表5 尺寸优化前后变化对比情况
由表5可知,尺寸变化主要体现在供水管外径与壁厚上,其缩减比例均在10%左右,悬臂的外径、壁厚尺寸缩减比例为2%左右,由此可见悬臂尺寸变化不大,而供水管为主要影响结构总质量大小的杆件。由于在力学性能分析中主要靠拉筋来承受结构内部的拉力,需保证其刚度、强度强度符合要求,拉筋半径在优化过程中基本没有变化。横向角钢和斜向角钢是结构的主要支撑体系,在严格保证刚度、强度的基础上,优化后角钢宽度缩减了10%,即其尺寸规格由56×6 mm优化到50×5 mm,适用于市场通用型钢尺寸规格。
由图4可以看出,优化模型结构质量变化曲线呈曲折下降至稳定持平的趋势,结构总质量由1 074.6 kg开始降低到800 kg左右稳定下来,结构总质量缩减比例为18.7%,优化效果较为明显。由于供水管与角钢尺寸为主要影响桁架结构质量的因素,如图5所示,显示了供水管与横向、斜向角钢的横截面积分别随优化次数相对结构总质量的变化情况:横向角钢横截面面积随有效优化次数呈现缓慢下降的趋势,斜向角钢横截面面积随优化次数的过程曲线呈现先快速下降,曲折中不断降低的变化趋势。

图4 优化模型质量变化过程曲线
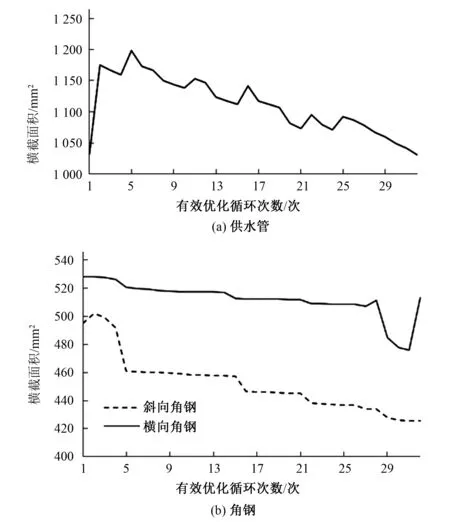
图5 供水管和角钢横截面积随优化次数变化情况
4 结 语
通过对轻小型移动式喷灌机桁架结构在3种工况下进行力学性能分析、结构验算及桁架结构尺寸优化后的结构分析,可得出以下结论:
(1)有限元APDL语言构建喷灌机桁架模型方便快捷,有利于后续对结构的力学性能分析和优化;对于相似喷灌机模型可采用同样方式架构,便于日后对类似结构进行对比分析。
(2)喷灌机桁架结构主要承受自重和水重荷载,最大变形往往发生在拉筋中部和两端悬臂,在喷灌机桁架结构设计过程中应考虑其结构合理性,验算过程中确保需确保杆件长细比和各杆件刚度、强度与稳定性符合相应要求,本文为喷灌机桁架结构力学性能分析提供了参考。
(3)风荷载对桁架结构的影响主要在于增加了最大弯矩,使得桁架结构较易倾覆从而影响结构的稳定性,对结构的刚度、强度则影响较小。故在风力较小的平原地区,无须过多考虑风荷载的作用,而在风力较大的高原地区,需酌情考虑风荷载对于喷灌机稳定性的影响。
(4)在满足桁架结构刚度、强度和稳定性的前提下,对喷灌机桁架结构进行尺寸优化有利于减轻结构质量、降低成本造价。尺寸优化效果较为明显,结构总质量缩减比例为18.7%,主要尺寸变化为供水管与角钢横截面,可根据优化后的截面尺寸设计喷灌机桁架结构。在对喷灌机简化模型尺寸优化的基础上,随着结构优化方法的日新月异,可对喷灌机的结构进行形状优化,进一步研究喷灌机桁架的合理结构形式,本文为日后喷灌机桁架结构的优化设计提供了借鉴。

