基于自抗扰控制器的稳定平台控制策略研究*

林海军，杨兆鹏，王贺，李莉

(哈尔滨理工大学 测控技术与通信工程学院， 哈尔滨 150080)

0 引 言

舰船在受到海浪、风等因素的影响的时候会出现船体摇摆不稳定的情况，而实际中往往需要保持摄像等载体能够一直保持稳定的状态。稳定平台实现了在受到多源扰动的情况下仍然能够保持稳定，隔离扰动对载体的稳定性影响。

稳定平台受到多源扰动影响，而这些扰动具有非线性、时变及参数不确定等特性，因此如何更好地隔离多源扰动是实现高精度稳定平台的核心。通常使用中PID对稳定平台的位置环进行控制，由于单纯的PID调节参数固定，面对突发的扰动时往往表现出动态性能较差，较难实现稳定平台的更高精度控制。因此需要设计应对多源、突发、非线性等扰动特点的抗扰动性强的高精度控制策略，满足载荷的稳定要求。国内外学者提出了各种先进控制方法来抑制扰动，取得了显著的效果：文献[1]提出了将自抗扰控制应用于平台系统速度环和常规PID控制的电流环构成的ADRC-PID控制，阶跃响应和跟踪性能得到了较大的提高。文献[2]设计了在自抗扰控制器中串入经典控制校正环节并应用于电流环的方法，结果表明采用改进型自抗扰控制器后频响曲线中的高频段被有效衰减。开环剪切频率为16.9 Hz，相位裕度为40°，带宽为40 Hz，谐振为1.23。文献[3]提出了一种基于电流环的自抗扰控制新方法以进一步提高航空光电稳定平台的抗干扰能力，结果显示系统的扰动隔离度至少提高了6.56 dB，随着扰动频率大于0.5 Hz，扰动隔离度最多可提高12.03 dB。文献[4]提出了使用改进型小脑模型关节控制器(CMAC)复合控制方法提高了航空稳定平台控制系统指向精度及稳定性。文献[5]提出了一种自适应前馈控制方法来提高惯性稳定平台稳定控制的指令跟踪性能，显著提高了系统的暂态性能。文献[6]提出了一种基于自适应灰色预测(AGPC)—分数阶改进干扰预测器(FIDOR)的稳定平台伺服干扰抑制方法，实验表明该方法不仅可以有效抑制稳定平台外界干扰和测量噪声，而且提高了系统响应能力。文献[7]设计了一个两步控制策略，首先将自抗扰控制设计为PID控制，然后利用Kalman滤波器对系统的状态扰动及测量噪声进行滤波消除，提高了整个稳定平台的隔离度。文献[8]设计了一种比例多重积分(PMI)观测器，有效的抑制了干扰力矩的影响，提高了平台的动态特性和稳态性能。

以上文献大多从速度环或电流环对干扰进行抑制，而在检测当前稳定平台位置时会引入传感器等外在干扰；而且，以往的控制策略大多采用“被动抗扰”的思想来提高平台的控制精度和稳定性，通过对当前值的检测和给定值进行比较后产生相应的控制量，容易使系统控制产生较大的控制延迟以及无法实现扰动的提前补偿。为了有效抑制位置环节引入的干扰，同时减小延时，文中研究基于“主动抗扰”思想的控制策略，即在位置环采用自抗扰控制器(ADRC)进行系统的控制。将影响载体位置发生变化的所有因素的和视为“总扰动”，根据对“总扰动”的估计对系统进行主动补偿，从而将扰动、不确定性和非线性的被控对象线性化为容易控制的“积分串联型”系统，提高系统的稳定性和精确度。

1 稳定平台系统模型及控制策略

1.1 稳定平台伺服系统模型

舰船稳定平台采用横滚轴、方位轴和俯仰轴三轴控制结构。每个单轴均从电流、速度、位置三个环节进行分析和设计，稳定平台系统结构框图如图1所示。控制回路由PWM功率放大驱动电路，力矩电机，平台负载、陀螺、加速度计、低通滤波器和控制器组成。

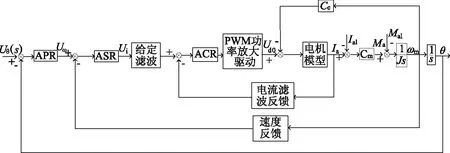
图1 稳定平台单轴控制框图

图1中Ce为电机的反电势系数，Cm为电机的力矩系数，J为电机转子与负载转动惯量之和。APR、ASR、ACR分别为位置调节器、速度调节器和电流调节器。在电流环采样电流中常常含有交流分量，为了不影响电流调节器对输出电流的影响，加入低通滤波器进行滤波处理，同时也产生了一定的反馈时间延迟，为平衡该延迟在给定信号通道上也加入同样的低通滤波器。将各模型参数代入到如图1所示的结构框图中得到稳定平台单轴伺服系统模型[9]如图2所示。

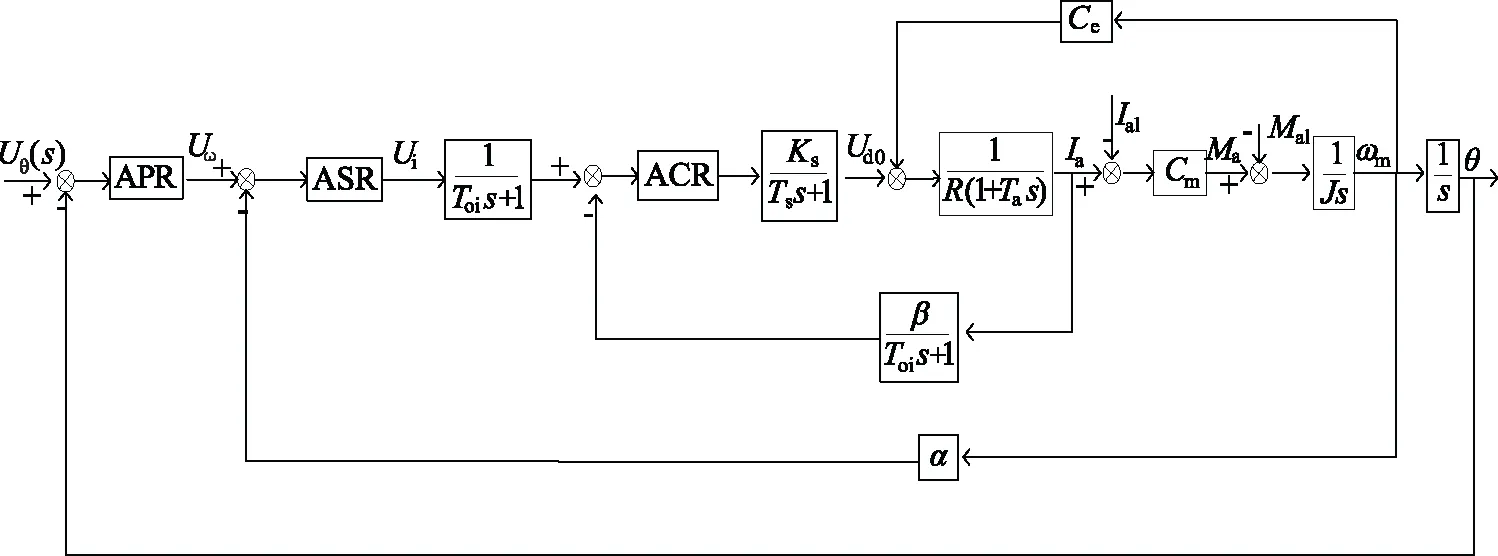
图2 稳定平台单轴伺服系统模型

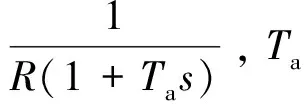
1.2 稳定平台控制算法策略

文中设计的稳定平台中电流环和速度环作为系统的内环，位置环作为系统外环[10]。电流环的作用是跟随电压指令变化，不发生电流突变，并且能够消除反电动势对输出力矩的影响，同时削弱低速运行时出现的“爬行”现象和避免换向时的“平顶”情况，电流调节器ACR采用PI调节[11]。

速度环对扰动作用敏感，容易出现速度波动的情况。因此通过速度调节器提高速度环对扰动的抑制作用使得伺服电机速度平稳，速度调节环ASR采用PID调节[12]。

位置环是稳定平台控制系统的核心环节，实现对目标指令的跟踪[13]，通过设计适当的位置调节器来保证系统的稳定精度和动态特性，位置调节器APR采用自抗扰控制器，其中的控制律采用PID进行控制。将所有对稳定平台位置产生影响的因素称为“总扰动”，通过ADRC对扰动进行估计，并且进行主动补偿，提高平台位置的抗干扰能力和对目标位置的稳定跟踪。

文中设计的系统内环采用经典控制策略，故不赘述。下面主要介绍系统外环的自抗扰控制器的设计。

2 稳定平台自抗扰控制器设计

稳定平台的目的是实现对平台扰动的抑制，平台位置跟随给定值变化。因此改善位置环的动态特性是实现高精度稳定平台的关键，根据单环机电模型，忽略高次项可以得出位置环控制对象为一个二阶系统，因此设计二阶自抗扰控制器[14]来实现对位置环的精确控制。

二阶ADRC框图如图3所示。ADRC主要由跟踪微分器(TD)，扩张状态观测器(ESO)，状态误差反馈控制率(SEF)三部分组成。其核心思想是根据被控对象输出y和控制量u的信息，以简单的“积分串联型”作为标准型[15]，把系统中异于标准型的部分作为影响控制位置的“总扰动”处理通过状态观测器进行对扰动进行实时估计，并利用控制率提前补偿扰动对系统的影响。

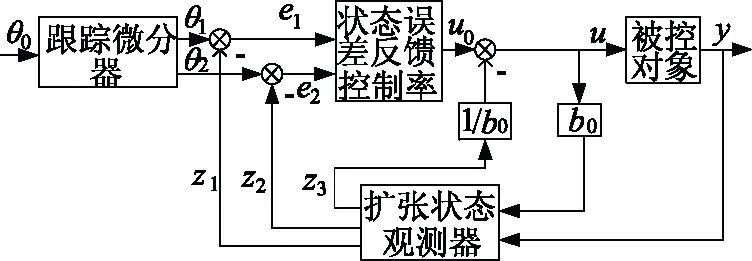
图3 自抗扰控制器结构图

(1)跟踪微分器(TD)：根据给定值θ0合理的安排系统过渡过程，使得输出曲线光滑、系统初始化过程平稳。θ1信号作为TD控制器的输入信号的跟随，θ2为输入信号的微分信号即θ1的微分；

(2)扩张状态观测器(ESO)：通过被控对象的输入信号u和输出信号y估计出对象的状态z1和z2以及系统总扰动z3，从而将带有非线性、不确定性的对象化为简单的“积分串联型”，实现对象的线性化和确定化;

(3)状态误差反馈控制律(SEF)：利用误差e1和e2，通过控制律主动补偿总扰动对平台位置稳定的影响。

2.1 跟踪微分器(TD)设计

跟踪微分器中θ1作为对给定信号的追踪可以直接得到值θ2，为输入信号的微分值，根据“快速最优控制”原理，采用“尽快的跟踪输入信号”的办法得到该微分信号。在设计中采用离散形式进行递推。设计的跟踪微分器为：

(1)

其中非线性函数fhan(e0,θ2,r,h)称为快速最优控制综合函数，具体函数关系式为：

(2)

式中θ0为TD的输入信号；θ1和θ2分别为TD的两个输出信号，其中θ1信号是对θ0信号的跟踪，θ2为θ1信号的微分信号，近似可以看做θ0的微分；e0是跟踪误差(或者残差)。在微分跟踪器中，具有两个可调参数r，h，“r”称为快速因子，r越大跟踪θ0越快，在确定参数时可以根据过渡过程的快慢和系统的承受能力来决定；h为采样周期。

2.2 扩张状态观测器(ESO)设计

ESO要实现的目的是根据被控对象给定值u和输出值y通过一定的控制规律构造出观测器，以便预测出系统的各个状态及未知扰动。

(3)

式中 ESO的增益βi=(i=1,2,3)为可调参数；补偿因子b0是对b的粗略估计；gi(e) (i=1,2,3)为构造的非线性函数，其函数形式为：

(4)

式中0<δi<1,δ>0为可调参数。

2.3 状态误差反馈控制律(SEF)的设计

通过ESO能够得到影响稳定平台位置的未知扰动的估计值z3，因此在控制律中进行补偿，其扰动补偿过程为：u=u0-z3/b0，通过设计已经将复杂的非线性、充满扰动的系统还原为标准的“积分串联型”系统，然后设计出相应的控制律，在文中我们使用常规PD来对误差进行控制和调节。其控制方式为：

(5)

式中kp，kd分别为控制律比例增益和微分增益，可调参数中一般取0<α1<1<α2,δ=n·h,n≥1。

2.4 ADRC控制器参数整定

ADRC控制器调节参数众多，采用隔离调节的方式来对进行，首先分别整定TD、ESO的参数，然后将这三部分综合，对控制律的参数进行整定。

(1)跟踪微分器参数的整定

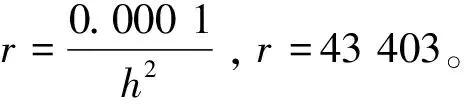
(2)扩张状态观测器的参数整定

ESO中核心调节参数为βi=(i=1,2,3)，在一般情况下选择β1h=1,β2和β3的取值可以按照β1进行取值，然后根据实际情况进行调节。b0的取值按照被控对象参数进行选择。

(3)控制律参数整定

根据以上各参数的整定值对PI调节中的参数进行整定，通过仿真验证参数的合理性。

3 仿真结果与分析

为了测试应用于位置环的自抗扰控制器的跟踪性能和扰动抑制能力，文章根据前文建立的稳定平台的系统模型进行系统仿真，分别采用正弦信号作为设定值输入测试跟踪能力；采用随机信号作为干扰测试扰动抑制能力，然后通过输出波形对系统性能进行分析。建立的稳定平台系统仿真模型如图4所示。

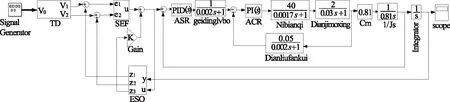
图4 稳定平台系统仿真模型

3.1 目标指令的跟踪实验

为了测试设计的控制策略的指令跟踪能力，在稳定平台系统的位置环输入幅值为1°，频率为1 Hz的正弦波形，利用搭建的系统模型测试平台位置跟随指令变化的响应曲线。得到的响应曲线如图5所示。

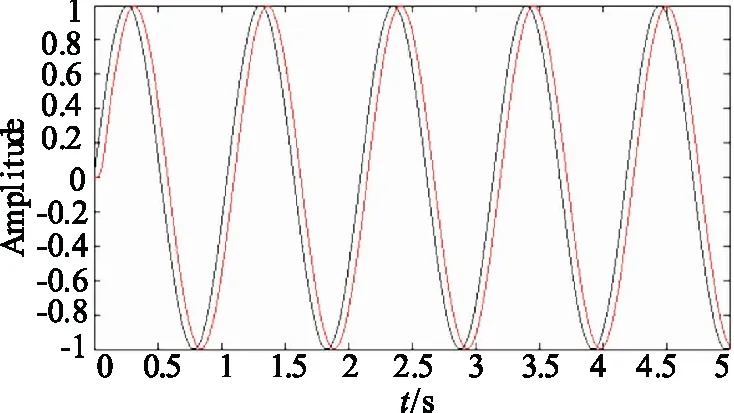
图5 位置跟踪响应曲线

从图5中可以看出，将自抗扰控制器应用于位置环之后，稳定平台系统视为“积分串联型”系统，该系统的稳定平台能够较好的跟踪指令位置，延迟时间大约为60 ms左右。而在位置环中采用PID作为调节器的控制策略中，测试的目标指令跟踪的延迟时间为100 ms，通过延迟时间比较可知，采用自抗扰控制器为位置环控制器的策略比PID的延时时间提高了40 ms，使得稳定平台控制系统能够更加快速的跟踪指令位置。

3.2 位置扰动实验

为了测试位置环自抗扰控制器对扰动的抑制能力，文中采取了在系统仿真模型中加入幅值为5°，频率周期为2 Hz和20 Hz的任意波形发生器模拟海洋扰动进行实验。可以得到如图6的不同频率的扰动响应曲线。

由图6(a)和图6(b)可以看到，随着频率的增大，相应的扰动响应曲线的尖峰的幅值也随之增大，最高峰值约为0.7°。在用于对比的采用PID做为位置环控制策略的稳定平台中加入同样的扰动时，扰动响应曲线的最高峰值为1.5°。对比响应曲线数据表明采用自抗扰控制器作为位置环控制器的稳定平台控制策略能够更好的抑制扰动作用，保证稳定平台的稳定。

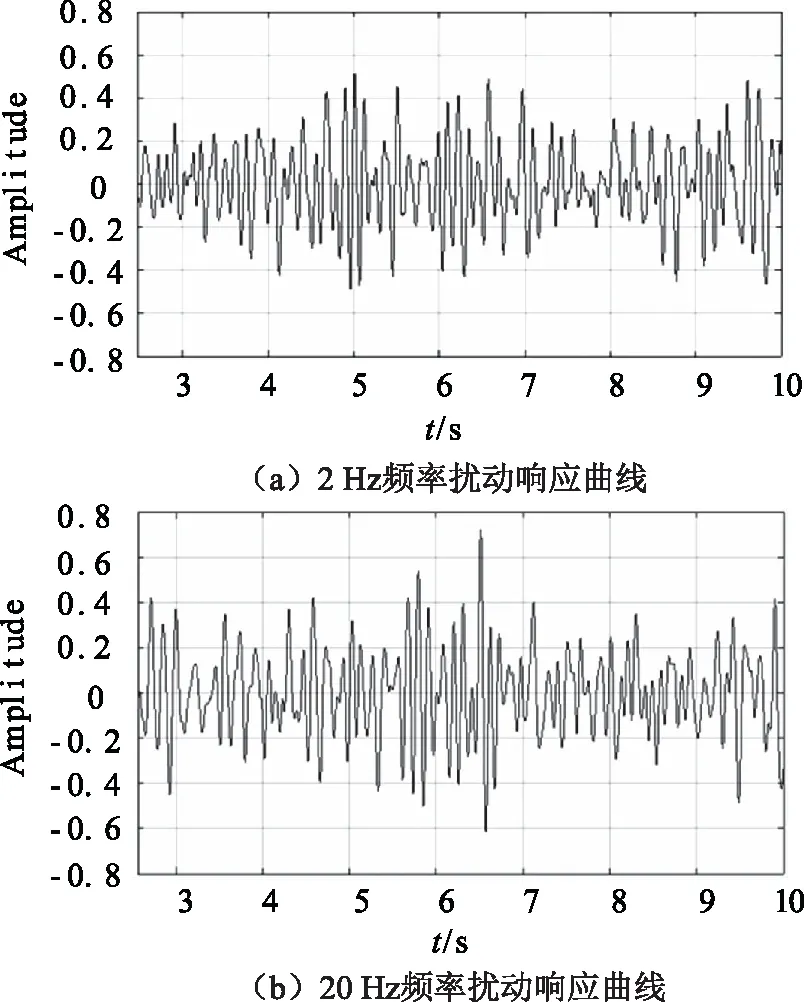
图6 不同频率的扰动响应曲线

4 结束语

文中设计了一种电流环采用常规的PI调节，速度环采用经典PID作为控制器，位置环采用自抗扰控制器的稳定平台控制策略。在稳定平台的跟踪延迟时间和扰动抑制两方面对设计的稳定平台控制系统进行了验证，与采用PID作为位置环控制器的稳定平台控制策略相比，位置指令跟踪延迟时间缩短了40 ms，扰动抑制能力提高了0.8°，稳定平台的跟踪能力和扰动抑制能力得到了显著的提高。