载重子午线轮胎热力耦合温度场的研究

黄京城，王 伟，2*

（1.青岛科技大学 橡塑材料与工程教育部重点实验室，山东 青岛 266042；2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

随着高速公路的快速发展和汽车性能的不断提高，车辆的行驶速度有了较大提高。与此同时，轮胎的温度伴随着行驶速度的提高而升高，导致物理性能下降，加速轮胎结构损坏。目前，对轮胎滚动温度场的研究主要有实测法和数值模拟法。利用试验方法只能对轮胎内部局部点的温度进行测量研究，无法为轮胎结构设计提供完整的温度场预测。而采用有限元数值模拟的方法可以根据轮胎不同的工况条件、材料特性等因素预测整个轮胎内部的温度场。

本工作采用单向解耦的方法[1-3]，将轮胎稳态滚动的温度场分析分解为3个模块：结构变形分析模块、能量损耗分析模块和热学分析模块。以12R22.5载重子午线轮胎为例，建立轮胎有限元模型，并将模拟结果与试验结果进行对比验证。在此基础上，增加轮胎生热、传热模型及热边界条件进行温度场数值模拟，同时研究不同行驶速度、充气压力、负荷等条件对轮胎温度场的影响。

1 轮胎结构变形模型的建立与验证

本课题组利用Abaqus有限元软件平台已经建立了子午线轮胎的结构设计、建模、计算分析等一系列完善的用于模拟分析轮胎静态接地与自由滚动的方案和策略。王伟等[4-5]已完成对12R22.5载重子午线轮胎静态接地工况的模拟与试验验证。本研究沿用相同方法得到的结果如表1所示。

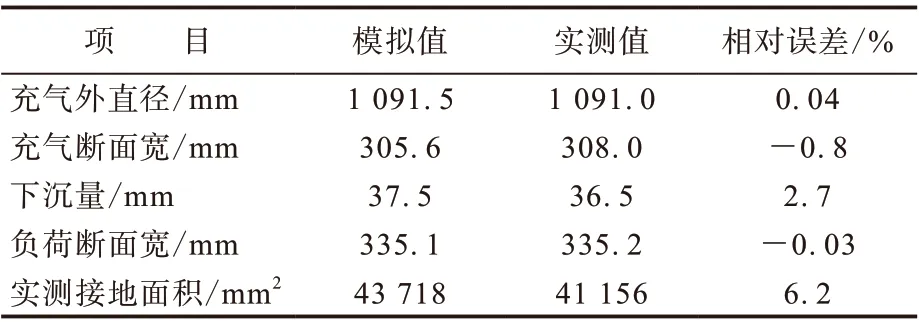
表1 轮胎标准工况下模拟值与实测值对比

标准工况下，模拟与实测的充气外直径、充气断面宽、负荷断面宽基本相同，下沉量的模拟值比实测值高2.7%。由于创建轮胎有限元模型时忽略了横向细小花纹的影响，轮胎模型的接地区域比实用轮胎多出横向花纹块的面积，因此接地面积的计算值高出实测值6.2%，但仍然满足工程问题研究的误差要求。可见，本研究建立的轮胎有限元模型与实测数据吻合较好，表明所建立的模型是正确合理的。

2 轮胎温度场模型的建立

2.1 轮胎的生热机理

轮胎是由多种橡胶材料与帘线组成的复杂结构，橡胶是典型的粘弹性材料，受到外力作用发生变形的过程中会产生滞后能量损耗。轮胎行驶过程中，各部位胶料不断经历周期性应力-应变循环，滞后损耗的能量转化为热量会使轮胎升温，内热源放热和轮胎与外界的热传导形成一个动态平衡的温度场。轮胎与路面的摩擦生热是其温度升高的另一个原因，但摩擦生热量只是较小的一部分，且生热发生在轮胎外表面，热量容易被周围空气带走，对轮胎内部温度分布影响很小。因此，本研究的轮胎温度场模拟只考虑滞后生热，忽略摩擦生热。

2.2 轮胎能量损耗分析

滚动的轮胎会产生周期性的应力（σ）和应变（ε），由于胶料的粘弹特性导致应变落后于应力，二者之间会出现相位差，导致滞后损失，因此二者的关系可以表示为：

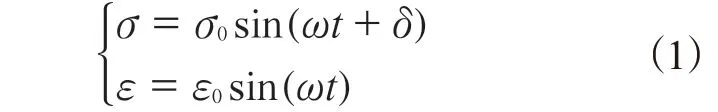
式中，σ0和ε0分别为应力和应变的振幅，ω为角频率，δ为滞后相位角。

橡胶材料在轮胎的一个滚动周期（T）内的滞后能量损耗（ξ）为：

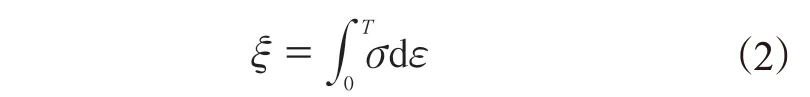
将式（1）代入式（2），则有

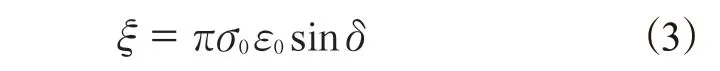
稳态滚动过程中轮胎的应力与应变循环是非谐变的。非谐变的应力与应变循环经傅里叶分解成一组谐波的叠加，得到不同频率的应力和应变值，具体如式（4）：

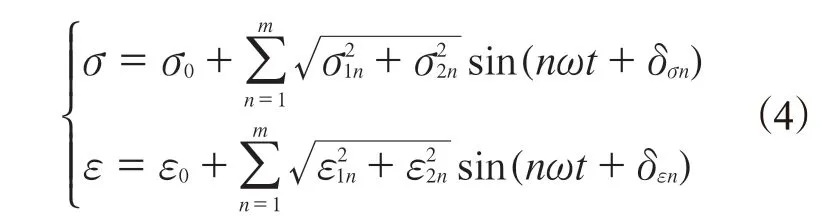
式中，m= 8时就能得到较好的近似值。

根据式（3）和（4）便可计算出轮胎各部位节点的滞后损耗能量（ξi）：

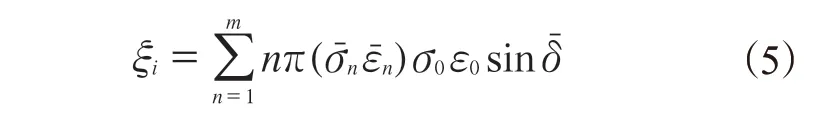
根据上述分析方法，编写能量损耗的计算程序，在轮胎变形分析结果中提取出各节点的应力、应变数据，然后在MATLAB中做相应的傅里叶展开，最后以式（5）实现各节点的能量损耗计算。

2.3 定义内热源

本研究利用有限元软件Abaqus的热学分析功能，以能量损耗数据结果计算的生热率定义轮胎的内热源。对于温度场的模拟分析，采取4种假设：（1）胶料的性能不受温度影响，能量损耗全部转化为热量；（2）温度呈稳态分布，在周向不会形成温度梯度；（3）轮胎处于热平衡状态，视为稳态热传导过程；（4）轮胎胶料各向同性。

热平衡方程可以表示为：

式中，t为时间；θ为温度；kx和ky为热导率；Q˙为生热率，经过网格离散后即为节点的生热率：

利用inp文件的关键词*Cflux将对应的数值赋予给变量flux（1），定义节点生热率。

2.4 定义轮胎温度场模型与热边界条件

根据假设（2），将热传导分析简化成平面轴对称问题，建立平面轴对称轮胎温度场的分析模型，如图1所示。轮胎模型各节点的生热率是从变形分析中得到的，为了正确定义节点的生热率，温度场模型与变形分析模型的网格保持完全相同。单元类型选用具有单个积分点的平面轴对称热传导单元DCAX4与DCAX3。为了便于结果的分析对比，在图1中分别标出了相同位置的胎肩节点841、胎圈附近节点510；A-A′和B-B′分别是胎圈附近、胎肩部位由内表面到外表面的取点路径。

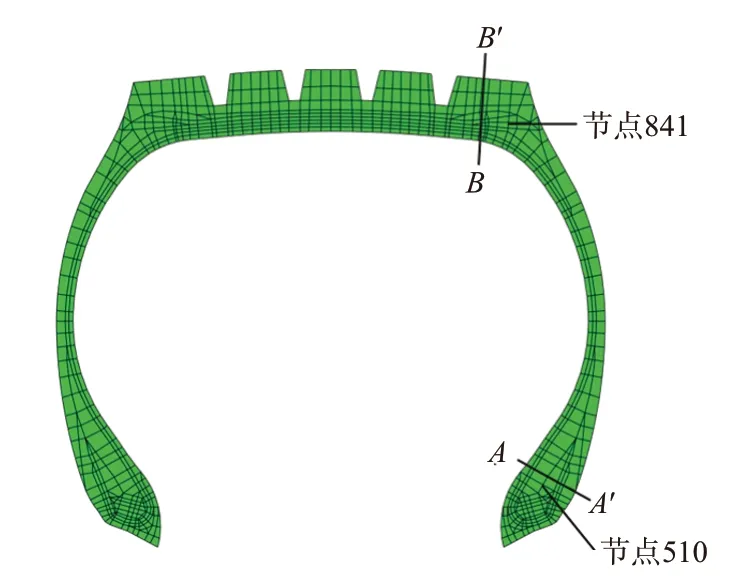
图1 平面轴对称温度场分析模型与特征节点位置

J.D.Clark等[6]采用试错法对轮胎各部位的对流换热系数进行了全面研究，并得出了结论，本研究以此来定义轮胎各边界的对流换热系数：hT=2.2v0.84，hB=1.4hT，hC=1.4hB，hS从hB到hT线 性变化。其中，hT，hC，hB，hS分别为轮胎的胎面、内表面、胎圈部位、胎侧部位的对流换热系数；v为轮胎滚动速度。

3 结果与讨论

采用有限元计算分析方法，对12R22.5载重子午线轮胎在不同速度、负荷、充气压力条件下的稳态滚动温度场进行数值模拟。

3.1 标准工况下轮胎温度场分析

图2所示为标准充气压力与负荷、100 km·h-1稳态滚动速度下12R22.5载重子午线轮胎的温度场模拟结果。

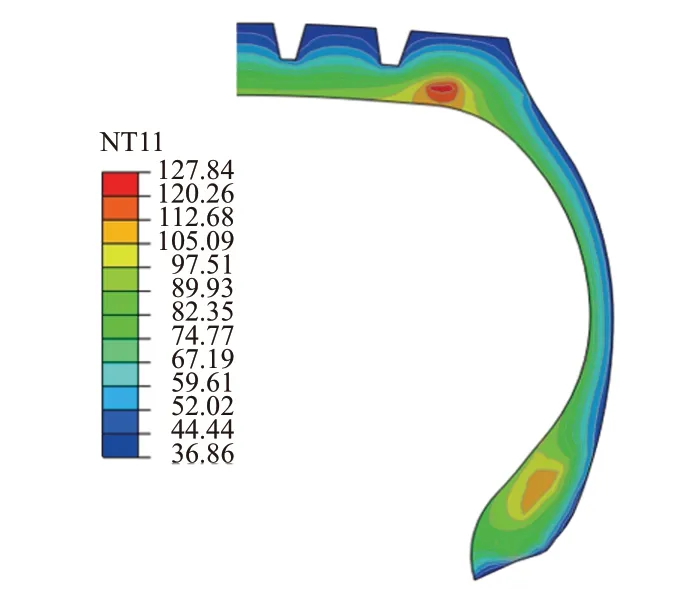
图2 标准工况下轮胎的温度场模拟结果

由于试验条件限制，本研究无法对该轮胎进行温度场试验测量。虽然相同条件下不同规格子午线轮胎的温度不同，但由于结构相似，其温度分布的特征和规律是基本一致的，因此，本研究将模拟结果与相关文献进行对比以佐证其正确性。对比文献[7]及其他相关文献[2-3]关于205/60R15子午线轮胎的温度场模拟结果可以看出，本研究轮胎高温区域主要分布在胎肩与胎圈附近，最高温度出现在胎肩部位，胎侧、胎面接近路面区域温度较低，与文献结果相符；同时文献[8]关于11.00R20载重子午线轮胎在标准工况、速度100 km·h-1条件下的胎肩温度实测值稳定在130 ℃左右，本研究模拟的胎肩最高温度为127.84 ℃，与文献值非常接近；文献[9]报道，11.00R20载重子午线轮胎在充气压力840 kPa、负荷32.70 kN、行驶速度80 km·h-1的条件下，胎肩部位温度实测值为85.8℃，本研究轮胎在速度80 km·h-1下相同位置的温度值为81.6 ℃。本研究关于12R22.5载重子午线轮胎温度场的模拟结果基本上符合轮胎实际温度分布情况。

图2的结果表明，胎肩的温度最高。胎肩由于路面挤压作用产生较大的应变，导致能量损耗增大，同时该部位较厚，产生的热量难以扩散，热量不断积聚导致温度升高。胎面直接与地面、外部空气形成热交换，大部分热量被带走，而胎侧较薄，产生的热量很容易向外部空气传导，因此胎面和胎侧温度较低。

3.2 不同速度下轮胎的温度分布

不同速度下轮胎的温度分布如图3所示。

由图3可以看出，不同行驶速度下轮胎的温度分布趋势与规律基本一致，高温区域位于胎肩和胎圈附近，最高温度均出现在胎肩部位，表明行驶速度不影响轮胎的温度分布特征和规律，但整体温度和最高温度会随轮胎行驶速度的提高而增大。行驶速度提高，轮胎滚动周期缩短，根据式（7）分析，胶料单位时间的生热率增大，从而使轮胎温度升高。

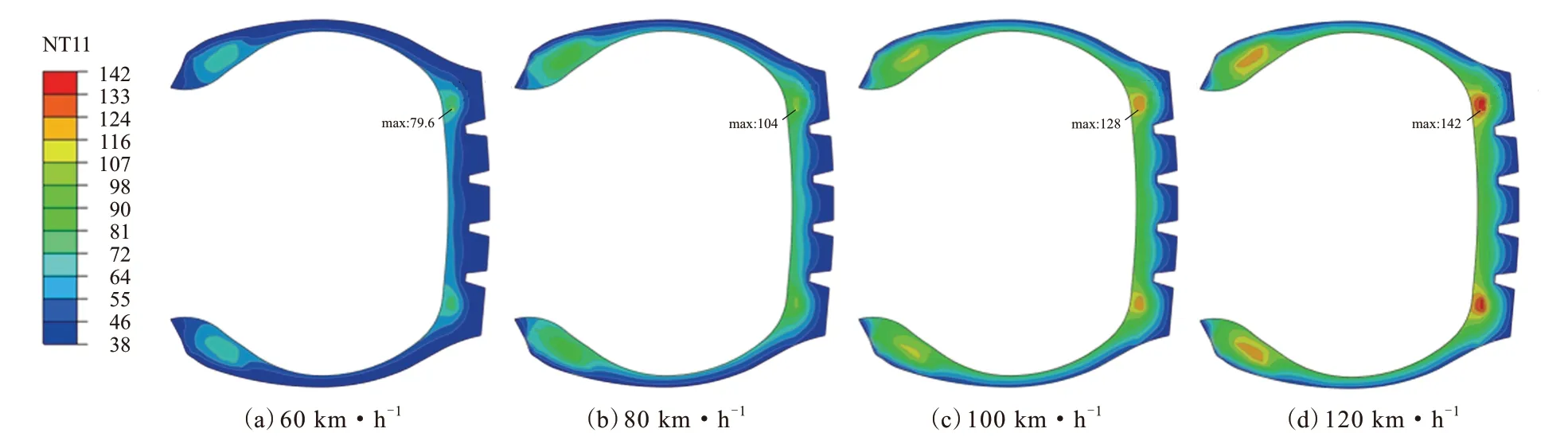
图3 不同速度下轮胎的温度分布

图4所示为行驶速度对胎圈、胎肩部位温度分布的影响。

图4 速度对胎圈与胎肩温度分布的影响

结果表明：行驶速度提高，这两个部位的温度均呈增大趋势；轮胎内部温度高于内外表面；内表面温度高于外表面温度，是由于内腔的空气封闭不流通且不断吸收热量所致。

3.3 速度、负荷、充气压力对轮胎内部节点温度的影响

速度、负荷、充气压力对轮胎内部节点温度的影响如图5所示。

从图5可以看出：随着行驶速度、负荷的提高，轮胎内部节点841和510的温度与轮胎最高温度均增大，3个位置的温度均随充气压力增大而减小；轮胎下沉量随着负荷增加而增大，胶料变形幅度增加，根据能量损耗分析，生热率增大，热量积累导致温升；充气压力对轮胎的影响与负荷类似，充气压力低于标准充气压力时相当于轮胎超载，高于标准充气压力时则相反。

图5 速度、负荷、充气压力对轮胎内部节点温度的影响

4 结论

（1）与相关文献比较，本研究所用方法模拟的载重子午线轮胎温度场分布符合轮胎实际情况。

（2）轮胎高温区域主要分布在胎肩和胎圈附近，最高温度出现在胎肩部位。

（3）随着行驶速度、负荷的提高，轮胎温度升高；充气压力增大，轮胎温度降低。因此，轮胎应尽可能在标准工况下使用，避免在超载、气压不足和超速情况下使用，否则容易导致轮胎使用寿命大幅度降低，并引起交通事故。

通过对滚动轮胎温度场的数值模拟，可以了解不同使用条件下轮胎的生热情况，降低轮胎的研究费用，缩短试验周期。