基于联盟博弈的综合能源系统优化运行方法

丛 昊, 王 旭, 蒋传文, 杨 萌

(1. 上海交通大学电子信息与电气工程学院, 上海市 200240; 2. 国网河南省电力公司经济技术研究院, 河南省郑州市 450000)

0 引言

近几年来,随着供给侧结构性改革的不断深入推进,以及能源产业政策的陆续发布,能源需求的总体格局和水平也在进行着日新月异的变化。传统的煤电逐渐向更多种类的清洁能源发电转型,加快了水电、核电、光电、风电、气电等多元化能源并举的局面,而国家发改委在2017年6月下发的《加快推进天然气利用的意见》中明确指出,鼓励风电、光伏等发电端配套建设燃气调峰电站,并同时开展可再生能源与天然气结合的多能互补项目示范[1]。该项措施推动了天然气市场的开启,使得天然气成为了中国未来重点发展的主体清洁能源之一。

区域综合能源系统(integrated community energy system,ICES)很好地实现了集成电、热、气等多种能源的综合能源系统的规划和优化运行控制,提高能源的综合利用率,同时减少用能过程中的环境污染[2]。国内外对ICES的优化调度问题有很多研究,文献[3-4]提出了考虑新能源接入不确定性的电—气互联系统的联合模型,并以经济性和环保性为最优准则进行ICES的优化调度。文献[5]采用区间数方法对光伏出力及负荷的不确定性进行建模,在同时考虑多能互补及环境效益的基础上建立了ICES日前经济优化调度模型;文献[6]在考虑了低碳成本的基础上对电力和天然气耦合系统进行稳态和动态建模,分析了耦合系统的灵活性和弹性;文献[7]考虑了风电和光伏的间歇性,建立了电力网络与热力网络的耦合协调调度模型,利用协调解耦算法对非线性优化问题进行求解。

为了能够更简洁方便地对综合能源系统进行统筹规划和调度,能源集线器(energy hub,EH)的概念应运而生[8]。基于EH模型的多能系统调度也有很多研究,文献[9-10]基于EH理论构建热电联产系统模型,给出了ICES的不同运行模式并提出相应的混合潮流算法与优化调度模型;文献[11]提出了基于EH的分层优化模型,在考虑用能替代的综合需求相应的条件下,建立ICES的多目标优化模型,利用模糊决策方法寻求最优解;文献[12-15]考虑了间歇能源、电价以及EH负荷需求等多种不确定因素,建立了综合能源系统的多阶段随机优化模型。

上述研究中都没有针对EH之间的相互协作运行进行研究,EH的运行都相互独立。随着智能设备的逐步普及,EH之间可以进行信息的交互,这样EH之间的相互协作运行不但可以提升ICES运行的灵活性,而且还能够降低弃风、弃光等间歇性能源的浪费。本文在文献[8]的基础上对EH模型进行扩展,构建了考虑风电及光伏等间歇性能源发电的EH模型;此外,文中在考虑了综合需求响应的综合能源系统双层优化模型的基础上,建立了适用于EH的不可转移支付联盟博弈模型,实现了EH之间能量的合作交互。相比于普通合作博弈方法,本文提出的模型算法在最大化利用可再生能源发电的前提下,可以获得更大的能源互补经济效益。

1 EH

1.1 EH模型

EH最早由Geidl于2006年提出[8]。从系统的角度来看,EH是一个能够为不同种类能源载体提供基本的输入输出接口、能源转换以及能源存储的结构单元[16]。因此,EH可以看作是传统电力系统网络节点的一种泛化或延伸。附录A图A1给出了一种简单且典型的EH结构示意图,其中包含了天然气、风能、太阳能、热能以及电能等多种能源,也包括了电力变压器、电热锅炉、热电联供以及燃气炉等多种能源转换装置,实现了多能源的耦合集成。本文的模型中暂不考虑储能设备。

在综合能源系统中,有很多种类的用能设施集群,如发电厂、工业厂房、大型建筑楼宇以及小型的城乡或城镇,都可以利用EH进行建模分析[17]。EH模型的建立不局限于系统的规模大小,它可以整合任意数量的能源载体,使得系统的建模更加灵活和简单。

附录A图A1中的EH共包含了6种能源转换装置(风机、光伏电板、变压器、电热锅炉、热电联供以及燃气炉),根据其耦合关系建立了能源的输入输出关系,如式(1)所示。

(1)

式中:Ew,Es,Pe和Pg分别为风能、太阳能、电能以及天然气的输入量;Le,Lh和Lg分别为电力、热力和燃气负荷;fw和fs分别为风机与光伏的输出函数;η为各转换器的能源转换效率;v为输入能源流入各转换器的调度系数(dispatch factor,DF),相应的η和v在附录A图A1中已标出。

其中调度系数满足以下关系[18]:

(2)

这里的分布式能源只考虑了风能和太阳能两种间歇性能源,在模型中,将其看作不可控或不可调度能源进行优先调用,则式(1)可以进一步整理为:

(3)

其中等号右端第1部分为可控量,EH可以通过调整外部输入的可控能源(电力、天然气)以及内部各转换器的调度系数来满足用户侧需求;等号右端第2部分为不可控量,EH将实际的风力及光照量所产生的电能输送给用户端使用。

1.2 智能EH

随着智能电网的逐步发展,智能集线器(smart energy hub,SEH)的概念应运而生[19-20],当传感器、智能电表以及嵌入式计算机等智能设备应用到EH当中后,EH便可升级为SEH。附录A图A2为SEH的简要结构图。

在SEH中,各种智能设备集成的能量管理系统(energy management system,EMS)将为EH中的转换装置控制器传递控制信号,使得SEH能够智能地调整运行优化策略,实时监控不同形式能源载体的运行状况,实现信息的双向通信。通过建立局域网络,传递的信息都可以被SEH捕捉,使得SEH能够更好地实现与能源公司和用户之间的相互协调,本文的研究即是建立在SEH基础上的。

2 考虑综合需求响应的综合能源系统优化模型

本节研究的综合能源系统包含了N个SEH,一个电力供应商和一个天然气供应商,能源供应商之间以及SEH之间的信息传递与合作在本节中不予考虑。能源供应侧将以能源价格为手段,激励用户侧参与需求响应以改变高峰时刻的用能量。这里建立了综合能源系统双层模型,上层为能源供应侧以最大化利益为目标提供能源,下层为SEH用户需求侧以最小化购能成本为目标优化运行,上下层之间以能源价格为纽带进行信息的交互,最终实现整个系统的最优化运行。

2.1 能源供应侧

能源供应商在保证满足用户需求的条件下最优化其目标函数,供需平衡关系如式(4)所示。

(4)

这里把最大化利润作为能源供应商的目标函数,利润为售能收益与供能成本之差,对电力和天然气供应商分别进行分析。

1)电力供应商

对于电力供应商,目标函数如式(5)所示。

(5)

式中:λe,t为电价,是时间t的函数;ce(·)为电力供应成本函数,通常成本为产生电能的函数,可以用式(6)所示的多项式函数表示[21-22]。

ce(x)=anxn+an-1xn-1+…+a0

(6)

式中:a0,a1,…,an为多项式系数。

为了能够保证电能的安全传输以及用户电能质量的需求,这里考虑如式(7)至式(9)所示的电力潮流约束,采用直流潮流形式。

(7)

-Plmax≤Pl≤Plmax

(8)

(9)

式中:q∈L(p)表示与节点p相连的节点;θp为节点p的相角;xpq和Bpq分别为节点p，q之间的线路阻抗和导纳;Pl为线路l的传输功率;Plmax为线路传输功率最大值;De,p为节点p的负荷;pg,p为节点p的发电机输出功率。

取发电边际成本作为电力价格如式(10)所示,根据电力供需平衡关系便可求得电力价格λe,t,而电价则是上、下层之间的纽带。

(10)

2)天然气供应商

同理,对于天然气供应商,目标函数为:

(11)

式中:λg,t为天然气价格,是时间t的函数;cg(·)为天然气供应成本函数。

取供应天然气的边际成本作为天然气价格,如式(12)所示。同样,根据天然气供需平衡关系便可求得天然气价格λg,t。

(12)

2.2 用户需求侧

传统电力用户参与需求响应主要有可中断负荷及可转移负荷两种方式,这两种方式都在一定程度上改变了用户的用电行为,而在有SEH的综合能源系统中,各种能源之间可以相互转化,增强了系统的灵活性,使用户的选择多样化,可以参与综合需求响应。所谓的综合需求响应是指电力用户在电价峰值的时段可以通过SEH将天然气或其他价格较低的能源转化成电能使用,避免购买高价电,从而减少购电成本[23]。这样,从用户的角度看,用电行为和负荷曲线并没有发生变化,仅改变了用电的来源,保留了用户原有的用电习惯;从电力供应侧的角度看,高峰时段的用电有削减,负荷曲线变平缓,供电可靠性提高。

下层用户需求侧目标函数为最小化购能成本:

(13)

式中：i=1,2，…,N。

式(13)给出了SEH从能源供应侧购买电能和天然气的成本。

式(3)给出了SEH的输入输出关系,这里对矩阵进行变换,得出用输出量表示输入量的表达式为:

(14)

式中：下标t表示时刻t,i表示第i个SEH。

这里假设风电和光伏的发电总和小于用户电力需求,即fw,i(Ew,t)+fs,i(Es,t)≤Le,t,i,且分布式能源被优先调用。

在综合需求响应中,负荷曲线不会改变,即Le,t,i和Lg,t,i不会随价格变化,SEH通过改变调度系数实现对价格的响应,进而改变SEH的输入量,从而达到目标函数的最优化。调度系数的取值范围为:

(15)

综上,下层最优化模型为:

(16)

式中：i=1,1,…,N。

2.3 双层优化模型

本节建立了考虑综合需求响应的综合能源系统双层优化模型。其中,上层为能源供应侧,以最大化利益为目标为用户提供能源;下层为用户需求侧,以SEH购能成本最小为目标优化运行。

3 基于联盟博弈的综合能源系统优化方法

在2.2节中,假设了分布式能源发电总量小于用户电力需求,而实际上风能和太阳能等都属于间歇性能源,此类能源发电量不可控,可能会大于用户电力需求,如果不考虑储能设备,就会出现弃风或弃光等能源浪费的现象发生。

为了能够减少能源的浪费并且最大程度地降低需求侧购能成本,SEH可以决定形成相互合作的集群,即联盟。当一个联盟S形成后,S中的每个SEH都可以根据其自身能源的盈缺,在联盟的内部进行能源的交互。这样,分布式能源发电量大于用户用电需求的SEH可以将多出来的电能卖出,从而增加收益并且减少能源浪费;同样,对电能有需求的SEH可以低价买入联盟中的新能源电力,从而降低其购能成本。在本节中,建立了一个适合于SEH的联盟博弈模型,并设计了分布式联盟构造算法进行求解。

3.1 SEH的联盟博弈模型

针对SEH之间的相互协作问题,定义其联盟博弈模型为C=(H,γ),其中H表示综合能源系统中所有SEH的集合,γ:2H→R表示每个联盟S⊆H的支付函数。为了给出每个联盟S的支付函数γ(S),首先要研究在某一时刻t,对于一个给定的联盟S,其中的SEH之间是如何进行协调运作的。

首先将任意一个联盟S中的SEH分为两类:卖方Ss和买方Sb,且Ss∪Sb=S,其中卖方Ss中的SEH有盈余的能源可以出售,买方Sb中的SEH对能源有需求。对于本文所建立的EH模型,只有电能可以由自身供应,天然气均需要从天然气供应商购买,因此这里仅通过每个SEH电能的盈余来对买方与卖方进行划分,即

(17)

然后针对每个联盟S,寻求卖方Ss、买方Sb以及能源供应侧之间的能源购售或传递关系。这里假设分布式能源发电的出售价格要低于电力供应商的电价,且Ss中每个SEH的盈余电能出售价格会因风机或光伏电板的不同而有所差异。对于一个给定的联盟S,假设其中买方Sb中共有k个SEH,这些买者以一定的顺序排列:Sb={b1,b2,…,bk},并且按照先后顺序购买所需能源,具体步骤如下。

1)买者bl以最小化其购能成本向卖者sl∈Ss购买能源,例如选择分布式能源发电出售价格最低的SEH。

2)如果卖者sl不足以满足买者bl的需求,则bl将从下一个最低价格的SEH购买剩余的电能需求。

3)买者bl重复上述步骤直至其用能需求得到满足或者联盟中没有再可以提供能源的卖者。

4)为下一个买者bl+1按照上述步骤寻找最佳匹配的卖者,直至Sb中的所有买者都完成匹配。

在上述过程中,所有SEH的天然气需求都将从天然气供应商购买。如果某个买者bl在上述匹配过程结束后仍有未满足的用能需求,它将从能源供应商侧购买;同样,如果Ss中的卖者最后仍有能源盈余,则会有弃光或弃风的情况发生。

在某一时刻t,对于任意给定的联盟S,设Π为Sb中买者的一种排序。对于任意一个排序Π,买方Sb的购能成本Cb为:

(18)

同理,卖方Ss的购能成本Cs为:

(19)

所有买者和卖者在联盟内部的购电成本和售电收入是相同的,即

(20)

根据式(18)至式(20),给出每个联盟S的支付函数γ(S)为:

(21)

式中:ΩS为Sb所有排序的集合。式(21)中的支付函数是使得联盟S中的SEH购能成本之和最小。

若γ(S)可以按照一定的规则公平分配给联盟S中的每个SEH,则这种博弈称作可转移支付博弈;若联盟S中每个SEH的支付值相互独立并且随联盟内协作策略的不同而会发生变化,则这种博弈称作不可转移支付博弈[25]。显然,本节所研究的博弈C=(H,γ)为不可转移支付博弈,对于某一时刻t,给定的联盟S中每个SEH的支付值φ为:

(22)

3.2 分布式联盟构造算法

3.1节研究了对于一个给定的联盟S,其内部的SEH是如何协作的,而本节将利用分布式联盟构造算法对集合H进行最优划分。

定义1:设A={A1,A2,…,Am}和B={B1,B2,…,Bn}分别为集合H的两种不同的联盟划分。对于一个SEHj,其在A划分中属于联盟Ai且支付值为φj(Ai),而在B划分中属于联盟Bk且支付值为φj(Bk),则有

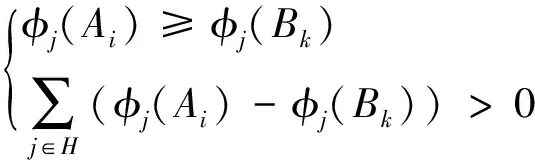
(23)

式中:A>B表示A划分优于B划分,这种联盟划分的比较排序称作帕累托序[26]。

式(23)表示如果联盟划分方式从B变到A使得每一个SEH的支付值都不会减少,且至少有一个SEH的支付值会增加,则A划分优于B划分。

在联盟构造算法中,采用两种分布式规则,分别为合并规则(merge rule)和分裂规则(split rule)[26],具体如下。

1)合并规则

2)分裂规则

对于一个联盟S,如果存在它一个划分{S1,S2,…,Sk}使得{S1,S2,…,Sk}>S,则将联盟S分裂为新的联盟集合{S1,S2,…,Sk}。

通过上述规则,若干个较小的联盟可以通过合并成为新的联盟,从而增加联盟中每个SEH的支付值;同样,较大的联盟也可以分裂成为多个较小的联盟以满足帕累托序。利用合并和分裂规则,设计了适用于相互协作的SEH的联盟构造算法,如附录A表A1所示。

在该算法中,给定集合N的一个初始划分S={S1,S2,…,Sk},首先进行合并过程:对于其中的任意一个联盟Si,按照合并规则寻找可以与其合并的联盟,如果有多个联盟满足可以与Si合并的条件,则选择合并后新联盟中SEH平均支付值最大的联盟。每当一个新的联盟通过合并形成之后,新的划分将进行分裂过程:每个联盟按照分裂规则进行分裂操作,如果有多种分裂方式可以满足分裂条件,则选择分裂后新联盟集合中SEH平均支付值最大的分裂方式。重复合并—分裂过程,直至没有联盟会有继续合并或者分裂的趋势,最终划分将收敛于最优的形式Sopt。该算法的收敛性详见文献[26]。

对于上述最优划分Sopt,按照3.1节的方法得到其中每个联盟中SEH的最优协作运行方案;然后在时间周期T内,利用分布式联盟构造算法求取不同时刻的SEH协作方案;最后按照2.3节的双层优化模型求解基于SEH联盟的综合能源系统最优运行策略。整体算法流程图如图1所示。

图1 基于联盟博弈的综合能源系统优化运行算法流程图Fig.1 Flow chart of coalition game based optimized operation method for integrated energy system

4 算例分析

4.1 算例概述

为了验证上述方法的可行性与有效性,考虑系统中有10个SEH、1个电力供应商以及1个天然气供应商,系统网络选取IEEE-30节点,网络数据及发电机数据详见文献[21-22],时间周期为T=24 h。其中,每个SEH的电力用户、热力用户和天然气用户数量分别都在区间[60,80]内,每个电力、热力和天然气用户的24 h负荷曲线如附录B图B1所示。

每个SEH内部各转换器的效率ηT,e,ηEB,h,ηCHP,e,ηCHP,h,ηFUR,h分别取自区间[0.9,0.98],[0.9,0.95],[0.4,0.5],[0.35,0.45],[0.93,0.97];每个SEH拥有风机和光伏发电的数量分别在区间[0,6]和[0,20]内,每台风机和每套光伏发电24 h出力曲线如附录B图B2所示。

4.2 计算结果及分析

这里分别对以下3种情景中综合能源系统的运行情况进行分析:情景1为不考虑综合需求响应和SEH联盟；情景2为考虑综合需求响应,但不考虑SEH的联盟；情景3为考虑综合需求响应和SEH联盟。

情景1不考虑综合需求响应,SEH总电力需求及电价曲线在图2中由蓝色曲线表示,从图2中可以看出系统24 h内有两个电力需求高峰时段,两个时间段内也出现电力价格尖峰,电力需求峰谷差为1 382.89 kW。同样,情景1的SEH总天然气需求在图3中由蓝色曲线表示,天然气需求高峰出现在晚间17至20时段。由于该情景不考虑综合需求响应,选取SEH3的调度系数vg,CHP为例,如图3所示,其值在24 h内为一条水平直线。情景1各SEH的24 h购能成本如表1所示,10个SEH总成本为1 365.47美元。

情景2中考虑了综合需求响应,SEH总电力需求及电价曲线在图2中由红色曲线表示,可以看出在高峰时段由于电力价格较高,SEH通过改变调度系数从而降低了该时间段内的电力输入量。因而从电力供应侧角度来看,电力需求曲线变平缓,电力需求峰谷差由情景1的1 382.89 kW减少为873.64 kW,削减了36.83%。情景2的SEH总天然气需求以及SEH3的调度系数vg,CHP曲线在图3中由红色曲线表示,可以看出在圆框内的用电高峰时段,由于电价较高,SEH调高了调度系数vg,CHP,从而增加了该时间段的天然气输入量以满足用户侧的电力需求。表1中给出了情景2各SEH的24 h总购能成本,10个SEH总成本为1 147.54美元,相比情景1,总成本减少了15.96%。

图2 情景1和情景2下24 h SEH总电力需求及电力价格曲线Fig.2 Curves of total electricity demand and price for SEH within 24 h under case 1 and case 2

图3 情景1和情景2下24 h SEH总天然气需求及SEH3的调度系数vg,CHP曲线Fig.3 Curves of total natural gas demand for SEH and vg,CHP of SEH3 within 24 h under case 1 and case 2

SEH编号总购能成本/美元情景1情景2情景3普通合作博弈 1158.23144.48131.26133.89 2142.49120.71114.21116.49 3108.3086.0979.6481.23 4146.40128.17120.65123.06 5110.4379.7170.5071.91 6131.03112.68105.74107.85 7106.4479.8074.7076.19 8122.2097.0389.3991.18 9176.27156.21147.07150.01 10163.68142.67135.11137.81 总计1 365.471 147.541 068.271 089.64

情景3考虑了SEH的联盟,即各SEH之间根据自身能源的盈缺情况相互协作组成联盟,从而减少购能成本。从附录B图B2中可以看出,风力发电在凌晨和晚间的出力较大,在白天出力较小,而风力发电又占分布式发电量的绝大部分,由前面的分析可知,只有在分布式发电量大于电力用户需求的时候才会产生联盟,因此本算例在t=1,2,3,4,5,16,22,23,24这几个时间段内会有联盟产生。这里以t=1时段为例,最终得到的联盟情况如附录C图C1所示。

附录C图C1中每个SEH下方括号内为分布式发电盈缺量,卖方为正,买方为负,箭头数值表示电能传输量,单位为kW。t=1时刻共形成了两个联盟:S1={EH5,EH6,EH9},S2={EH1,EH3,EH4,EH7,EH10}。S1中EH5为电力盈余125.09 kW的卖者,EH6和EH9分别为有电力需求42.17 kW和81.77 kW的买者,S1按照附录C图C1箭头所示进行电能买卖,最终EH5剩余1.15 kW分布式发电量将被舍弃;S2中EH3和EH7分别为有电力盈余52.06 kW和92.57 kW的卖者,EH1,EH4和EH10分别为有电力需求75.17 kW,32.45 kW和34.65 kW的买者,S2按照附录C图C1箭头所示进行电能买卖,最终EH3剩余2.36 kW分布式发电量将被舍弃。卖方EH3,EH5,EH7的分布式发电价格为8.78,8.23,8.60美元/(MW·h),EH2和EH8也有电力盈余,但两者电价分别为10.61,10.10美元/(MW·h),价格较高,为达到购能成本最低的目标,在形成联盟时EH2和EH8未被选中。t=1时段联盟合并和分裂过程及购能成本变化见附录C表C1,SEH经过4次合并与分裂最终达到最优的联盟协作方案,该时刻的购能成本从第1次合并分裂的41.51美元减少到第4次合并分裂的32.51美元,减少了21.7%,说明了联盟形成可以有效降低SEH购能成本,实现更大的能源互补收益。

按照本文所提出的联盟博弈构造方法,可以得出每个时间段SEH的联盟情况,最终求出SEH总电力需求,如图4所示。由图4可以看出，虚线圆框内为有联盟形成的时间段,相比于情景2,这些时间段内SEH的电力需求有所减少,即可说明SEH之间的联盟行为可以减少用户对能源供应侧的依赖,减轻能源供应侧的供能压力,同时增强了用户的灵活性和自给自足能力。

图4 情景2和情景3下24 h SEH总电力需求曲线Fig.4 Curves of total electricity demand for SEH within 24 h under case 2 and case 3

该算例中分布式能源发电24 h总量为35.47 MW,情景1和情景2中弃风或弃光量为1.15 MW,情景3中的弃风或弃光量为0.14 MW,减少了约87%,能源浪费大幅度降低。表1中给出了情景3各SEH的24 h总购能成本,10个SEH总成本为1 068.27美元,相比情景2,总成本减少了6.91%,虽然成本降低比例较少,但当系统变大时所节约的成本还是可观的。附录C图C2给出了SEH平均购能成本随其数量变化曲线,可见随着SEH数量的增多,情景3中SEH的平均购能成本逐渐降低,联盟的优势逐渐体现出来。

相比于普通的合作博弈,即为联盟博弈中10个SEH合并成为一个大联盟的情况,表1中同时也给出了普通合作博弈下各SEH的24 h购能成本。对比可见,采用联盟博弈的购能成本要优于普通博弈的结果,更加证明了本文所提出方法的有效性和经济性。

5 结语

本文考虑了风电和光伏等分布式能源发电以及综合需求响应,建立了基于SEH的综合能源系统双层优化模型,并提出了一种基于联盟博弈的综合能源系统优化运行方法,利用分布式联盟构造算法进行求解,最后通过算例验证了方法的有效性。研究结果表明,本文所提出的方法可以有效地削减能源供应侧角度的用户需求峰谷差,大幅度降低弃风或弃光等间歇性能源的浪费,减少SEH用户侧的购能成本,同时增强了综合能源系统的灵活性,使得用户之间可以在联盟内部进行能源的买卖与交互,减轻负荷侧对能源供应侧的压力;当系统变大,SEH数目变多后,联盟对于综合能源系统的优化运行带来的经济利益将更加明显。本文的研究中未考虑储能设备,在以后的工作中将对储能的参与和调度运行进行研究,并加入不确定因素的分析。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。