干燥带对绝缘子温度场影响的研究

， ，，，，

(青岛科技大学，山东 青岛 266061)

0 引言

绝缘子污闪主要可分为绝缘子表面积污、污层受潮、形成干区、产生局部电弧、局部电弧延伸产生闪络5个阶段。绝缘子表面干燥带的产生使污秽绝缘子表面电场分布极不均匀，干燥带两端承担了大部分电压，电场强度变大，当干区电场强度达到一定值时会导致干区产生火花放电或电弧放电，甚至直接产生污闪事故，由此可知干燥带与局部电弧的产生和污闪的发生密切相关。因此对干燥带产生时绝缘子表面的发热机理的研究具有重要意义。

1 绝缘子干燥带形成原因

绝缘子表面被染污湿润后会产生泄漏电流，若流经染污层会使其温度升高，当达到一定值时会引起染污层水分蒸发，因为绝缘子表面温度分布是不均匀的，所以染污层水分蒸发速率不同，故在绝缘子表面温度较高水分蒸发较快的位置产生干燥区。干燥区的生成会导致绝缘子表面染污层电阻分布不均匀，绝缘子两端电压聚集在干燥区两端，使干燥区温度急剧增加，水分蒸发加快，最终形成一个或者多个狭窄的干燥带。假设绝缘子表面染污均匀，湿润后表面绝缘性能降低，两端施加电压将会产生泄露电流，假设表面染污层水分蒸发的速率保持一致时，表面染污层的电阻率也保持一致，这时绝缘子染污层不会产生干燥带，在绝缘子表面单位面积内有：

(1)

P为绝缘子表面单位面积的发热功率；E为单位面积内的电场强度；J为泄露电流密度；ρ为单位面积的表面电阻率。

当绝缘子表面出现干燥带且绝缘子两端施加交流电压时，绝缘子等效电路相当于绝缘子表面电阻和极间电容并联。当施加直流电压时，绝缘子只与表面电阻有关，所以只分析绝缘子两端施加直流电的情况。绝缘子表面发热功率的分布主要依据绝缘子表面电阻的分布，因此将绝缘子表面染污层看作一系列阻值不相等的电阻串、并联组成，建立的污秽绝缘子表面等效电阻模型如图1所示。

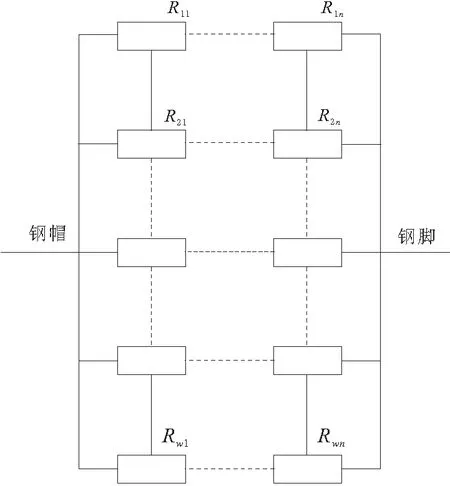
图1 绝缘子表面电阻模型

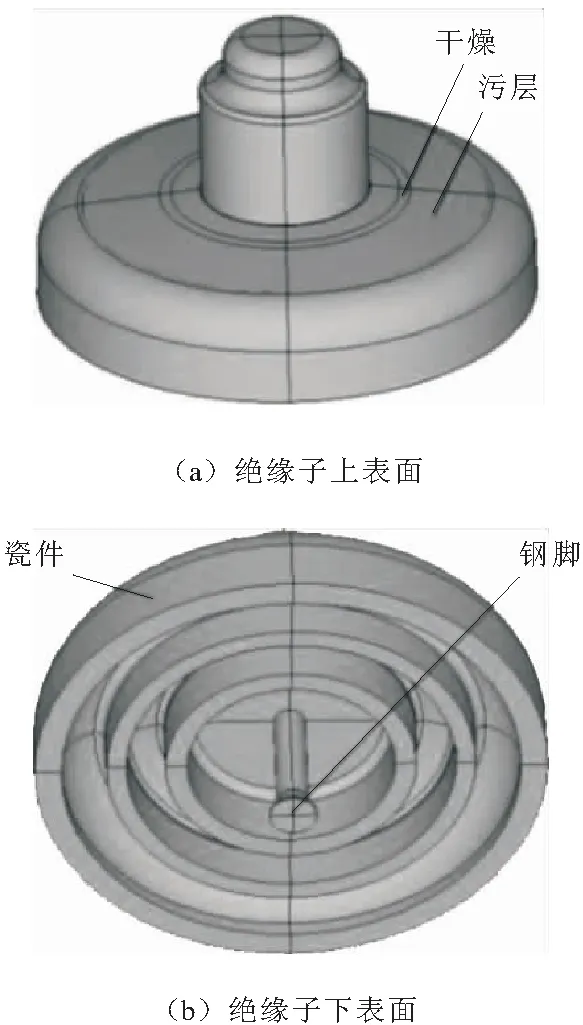
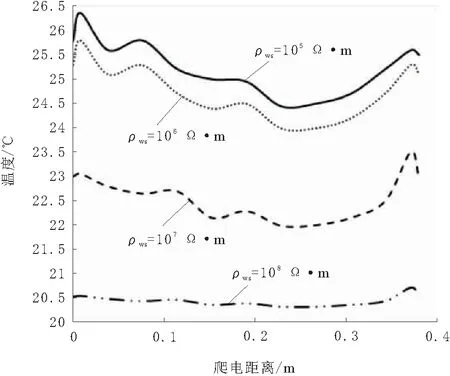
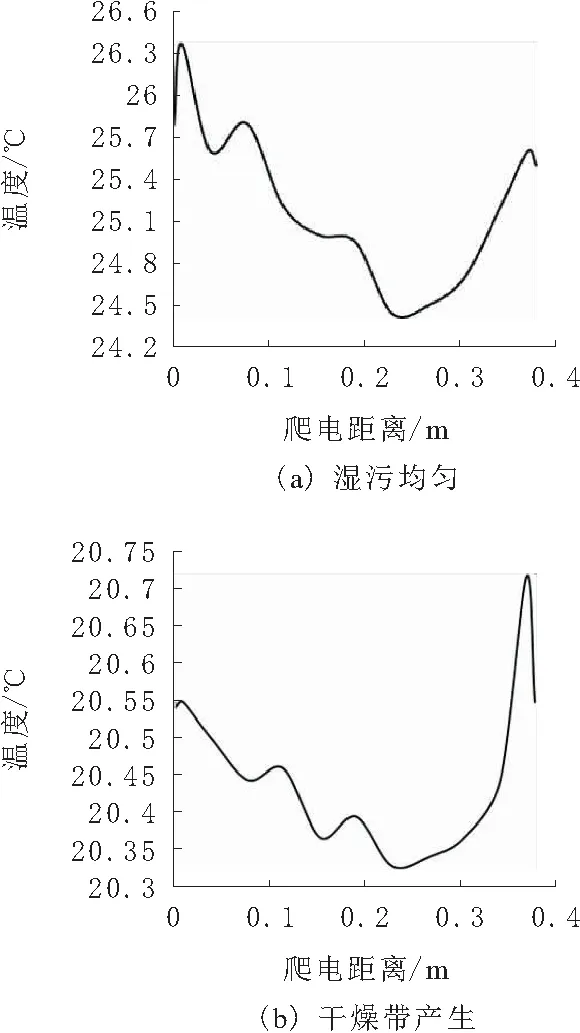
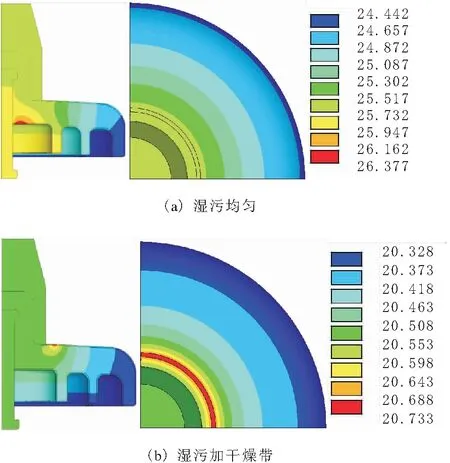
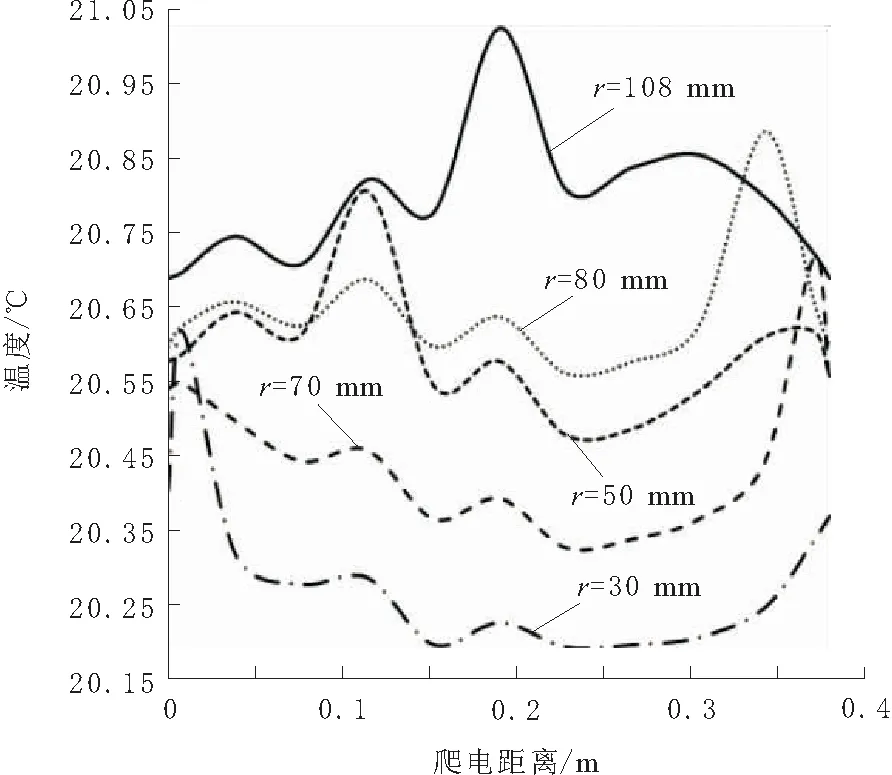
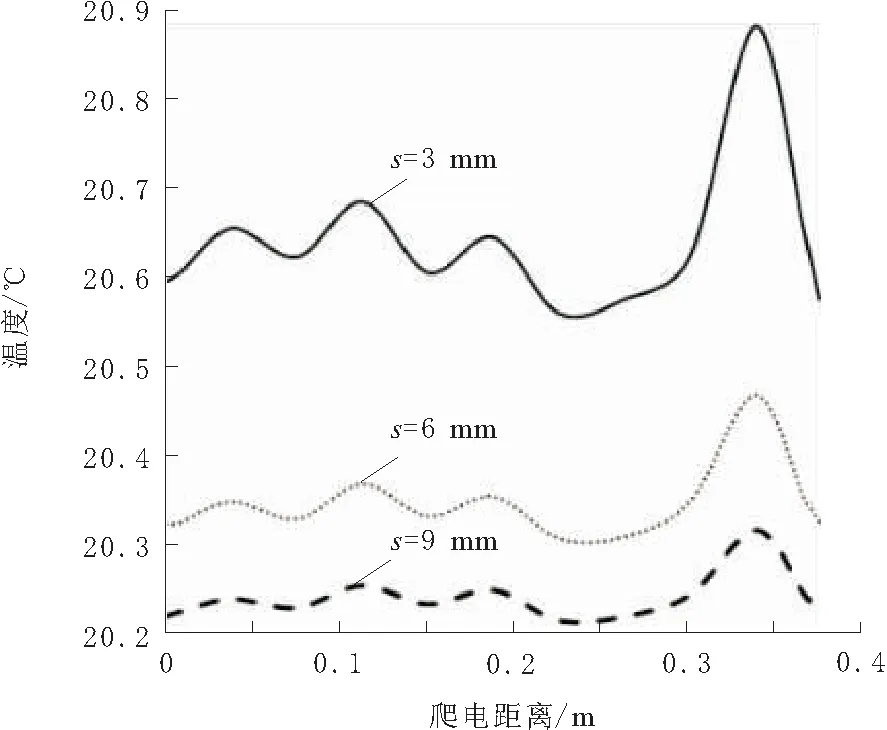
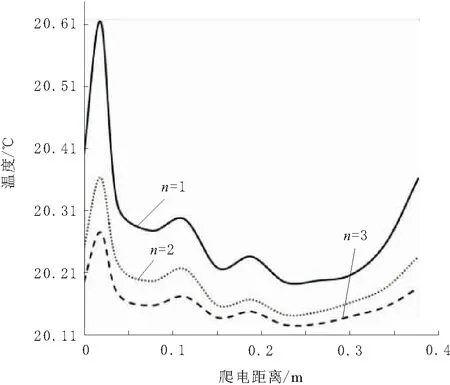
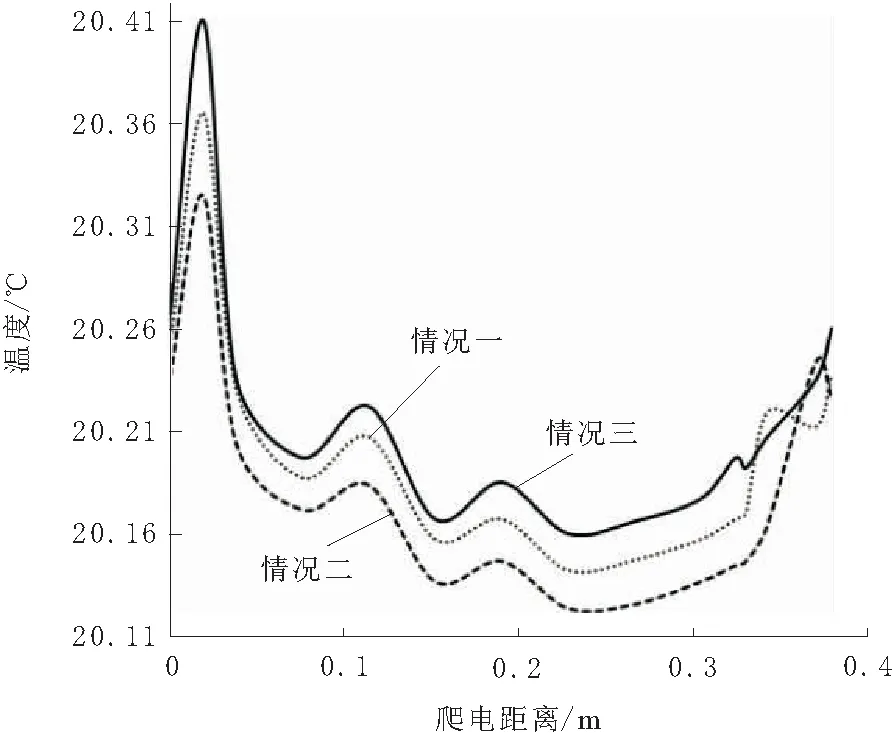
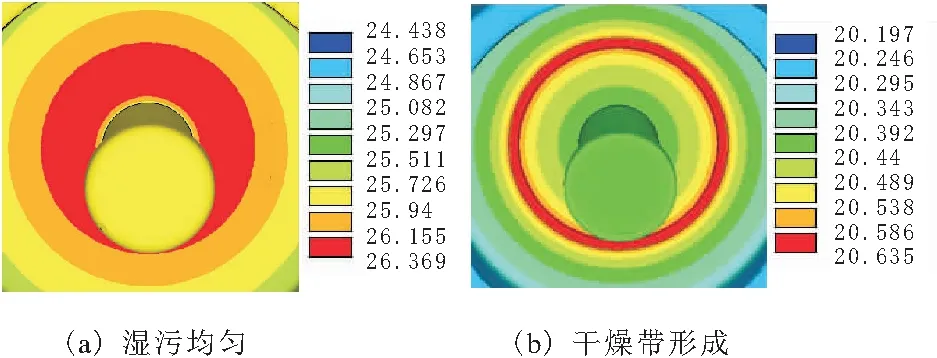
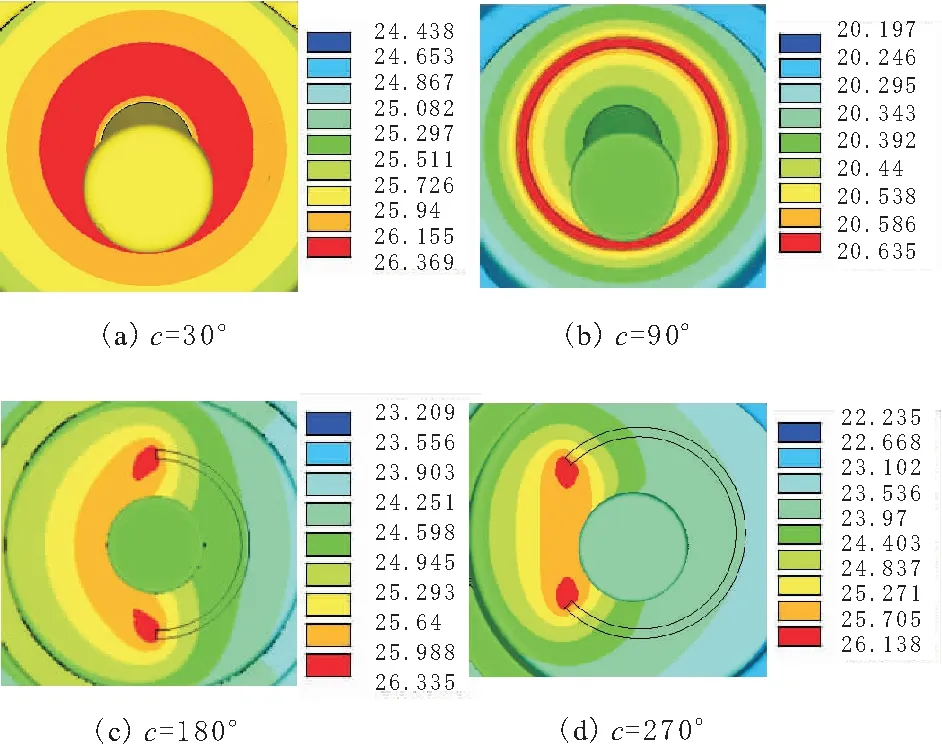
绝缘子表面边沿处等效半径最大，因此越靠近边沿处的电阻阻值越小，即R11>R12>…>R1k<…

2 绝缘子分析模型

绝缘子发热包括介质极化损耗发热、内部穿透性泄漏电流发热和表面泄漏电流发热3部分。染污绝缘子受潮表面湿润，污秽层电导率上升，电阻下降，导致表面泄漏电流大幅度增大，表面发热功率大幅度增大，得出绝缘子的发热功率以表面泄漏电流发热为主。因此在分析时只考虑表面泄漏电流发热。

在湿污状态下，绝缘子串的电压分布主要受表面绝缘电阻的影响，同串绝缘子污湿状态相似，导致各绝缘子承载电压基本一致，发热情况也基本相同[1]。而出现干燥带时电压大都施加在干燥带两端，故分析单片绝缘子的温度分布即可，以XP- 70线路盘形悬式瓷质绝缘子为对象，研究单片绝缘子表面的温度分布。根据实际情况可知绝缘子表面有泄露电流发热，同时还有向内的热传导以及在整个绝缘子外表面的对流散热，热平衡状态下辐射散热对绝缘子表面温度影响较小[2]，不对其分析。

2.1 确定分析参数

借助ANSYS有限元软件进行分析。绝缘子湿污之后以表面泄露电流发热为主，根据上述条件得到绝缘子的控制方程为导电和导热的联立方程组为[3]：

(2)

σ为导电率；V为电位；T为温度；λ为导热系数；qVOL为控制单元的焦耳热。

确定分析参数：在110 kV输电线路中绝缘子串两端承受的相电压为63.5 kV，一串一般包括6～7片绝缘子，1片绝缘子上平均压降约为10 kV，为了尽可能模拟实际运行情况，模型施加电压选为10 kV。环境温度为20 ℃，空气自然对流时换热系数范围为1～10 W/(m2·K)，由于干燥带电弧多产生在风速较小的情况下，故取对流换热系数为10 W/(m2·K)，用绝缘子表面覆膜厚度1 mm模拟污层，用污层电阻率模拟污秽情况，其余参数如表1所示。

表1 分析参数

2.2 确定单元建立模型

ANSYS电热耦合分析时单元选取Solid69，此单元为热电六面体单元，需定义参数为电阻率和导热系数，因文献[4]中阐述绝缘子湿污时介电常数对绝缘子电场分布的影响远小于电阻率的影响，因此忽略介电常数的影响，根据文献[5]建立绝缘子模型，如图2所示。

图2 绝缘子模型

3 干燥带的产生过程

假设绝缘子初始状态为湿污均匀状态，由于干燥带的产生具有不确定性，现指定干燥带产生位置为上伞盘r=50 mm处，宽度为3 mm。绝缘子为轴对称模型，干燥带呈环状分布，在干燥带产生过程中湿污层电阻率不变，因此运用ANSYS软件建立绝缘子四分之一模型进行分析，分别取干燥带产生区域污层电阻率ρws=106，107，108，109Ω·m来模拟绝缘子从湿污均匀到干燥带产生的过程，根据模拟结果得到绝缘子从钢脚处沿爬电路径的温度变化情况如图3所示。图3中横坐标0～0.228 m为绝缘子下伞盘面，0.228～0.379 m为绝缘子上伞盘面。

由图3可知，电阻率越小，绝缘子从钢脚处沿爬电路径的温度越高，尽管电阻率大小不同，但是绝缘子从钢脚处沿爬电路径的温度变化曲线形状大体一致。

图4为不同湿污程度下温度沿爬电路径变化曲线。由图4可看出，爬电距离为0.228 m处即绝缘子边缘处温度最低；未产生干燥带前钢脚附近温度最高，干燥带产生后干燥带处温度最高；绝缘子湿污均匀不产生干燥带情况，绝缘子达到热平衡后整体温度最高，绝缘子表面最高与最低温度差值最大，沿爬电路径温度变化情况如图4a所示；当绝缘子产生干燥带时，随着干燥带产生区域污层，电阻率增大温度开始下降，最高与最低温度差值开始减小，干燥带产生时温度分布情况如图4b所示。由图4可知，干燥带形成后干燥带处温度最大。

图3 钢脚处温度沿爬电路径变化曲线

图4 不同湿污程度下温度沿爬电路径变化曲线

对比图4a与图4b可以发现，湿污均匀情况与湿污加干燥带情况的径向温度分布差异很大，湿污均匀时钢脚附近温度最高，下伞盘温度波动是由于绝缘子结构造成的，而湿污加干燥带情况，上伞盘干燥带处温度最高，下伞盘温度差值变小，这一特点为红外检测提供了依据。

湿污均匀情况与湿污加干燥带情况热平衡后的温度分布云图如图5所示。由图5可看出。绝缘子表面平均温度在湿污均匀情况下高于湿污加干燥带情况下，在湿污均匀情况下，钢脚处温度最高，在湿污加干燥带情况下，干燥带位置温度最高。2种情况下都是绝缘子边缘温度最低。

图5 绝缘子热平衡温度分布云图

从图1绝缘子表面电阻等效模型来解释干燥带的产生对绝缘子温度场的影响。在模拟中假设干燥带产生位置为上伞盘r=50 mm处，宽度为3 mm，为环状分布。假定R为干燥带等效电阻，随着此处水分蒸发,R的阻值随之增大，施加在R两端的电压降增大，场强增大，所以电阻R发热功率增加。从整个绝缘子来看整体电阻增加，泄露电流降低，而施加在绝缘子两端的电压不变，所以绝缘子整体产热量下降温度降低。

由式(1)可知，单位面积内发热功率与单位区域内电场强度和表面电阻率有关，由图4a可以看出绝缘子湿污均匀时钢脚附近发热功率最大，这是由于钢脚附近场强最大，虽然钢脚附近电阻率也很大但并不占主导作用，因此绝缘子湿污均匀时表面温度的高低可以根据场强大小来判定。

4 干燥带对绝缘子温度场的影响

4.1 干燥带位置对绝缘子温度分布的影响

绝缘子污层水分蒸发受污秽、雾以及空气流动速度等因素的影响，很难保持一致[6]，因此干燥带的产生位置具有随机性。为了研究干燥带出现在绝缘子表面不同位置时的绝缘子径向温度变化情况，现分别取上伞盘r=50 mm，r=80 mm，下伞盘r=30 mm,r=70 mm,r=108 mm处，宽度为3 mm的干燥带进行模拟，观察干燥带位置对绝缘子表面温度场的影响。结合文献[7]以及图6得出，随着绝缘子干燥带产生的位置离对称轴越远，绝缘子整体温度越高，当干燥带位于r=108 mm时，绝缘子的温度最高。虽然绝缘子温度随着干燥带径向位置的增大而增大，但是整体温度变化不大。

从图1绝缘子表面电阻等效模型来解释干燥带产生位置对绝缘子温度场的影响。与其他位置产生干燥带的情况相比，在绝缘子边缘处产生干燥带时绝缘子整体电阻较小，泄露电流变大，由式(1)可知此情况下绝缘子发热最大，因湿污层电阻率变化很小，所以绝缘子整体温度最高。由图6也可看出，越靠近边缘处干燥带产生后绝缘子整体温度越高，验证了上述理论。

绝缘子表面轴向不同位置形成干燥带时，靠近两电极处形成的干燥带场强较大；靠近绝缘子边沿处形成的干燥带场强较小且最大场强随沿面距离减小较慢，高压电极附近形成干燥带时场强最大[8]。由图6可知,并不是场强最大处产生干燥带其温度最大，由此可看出污秽绝缘子表面发热功率是由表面电阻率与场强共同决定的。

图6 不同干燥带位置上温度沿爬电路径变化曲线

4.2 干燥带宽度对绝缘子温度分布的影响

研究干燥带宽度对绝缘子温度分布情况的影响，现取宽度s=3 mm，s=6 mm，s=9 mm，位置位于上伞盘r=80 mm处，绝缘子表面温度沿爬电路径变化情况如图7所示。

由图7可知，绝缘子温度分布变化曲线随着干燥带宽度增加在温度最高点附近温度变化率减小；同时随着干燥带宽度的增大绝缘子整体温度下降且最高温度与最低差值变小。

图7 不同干燥带宽度下温度沿爬电路径变化曲线

从图1绝缘子表面电阻等效模型来解释干燥带宽度对绝缘子温度场的影响。假定R为干燥带等效电阻，干燥带宽度增加，R阻值增大，绝缘子表面的总体电阻增加，泄露电流减小，在两端电压不变的情况下发热功率减小,因此绝缘子整体温度降低。由于干燥带处电阻率最大，所以干燥带处发热功率最大，温度最高。

4.3 干燥带条数对绝缘子温度分布的影响

绝缘子染污层表面有时可能同时产生多个干燥区，发展为多个干燥带。现研究干燥带条数对绝缘子温度情况的影响，取干燥带条数n=1，n=2，n=3，位置分别为下伞盘r=30 mm，下伞盘r=30 mm，r=70 mm；下伞盘r=30 mm，r=70 mm,r=108 mm，宽度为3 mm，根据模拟结果绘制曲线如图8所示。

图8 不同干燥带条数下温度沿爬电路径变化曲线

由图8可知，干燥带同在绝缘子下伞盘，随着干燥带条数增加绝缘子整体温度下降，靠近钢脚处的干燥带温度最高；远离钢脚的干燥带在温度曲线中表现并不明显。因此可以看出，多条干燥带位于绝缘子同一面时，离两极越近的干燥带对绝缘子表面温度的影响越大。

当干燥带为2条，一条位于下伞盘r=30 mm处，另一条分别位于上伞盘r=50 mm,r=70 mm,r=100 mm处时，分别定义为情况一，情况二，情况三，得到温度变化曲线图9所示。

图9 温度沿爬电路径变化曲线

从图9中可以看出，当绝缘子上下伞盘同时有干燥带时，离钢脚越近干燥带温度越高。上伞盘干燥带处温度有起伏变化，但并不明显，上伞盘干燥带越靠近边缘绝缘子整体温度越高。

在模拟中假定绝缘子产生2条干燥带，一条位于绝缘子下伞盘r=30 mm处，另一条分别位于上伞盘r=50 mm，r=70 mm，r=100 mm处。同为2条干燥带，下伞盘干燥带位置固定不变，当上伞盘干燥带越靠近边沿处的电阻，阻值越小，因此上伞盘越靠近边沿处，绝缘子整体电阻值越小，泄露电流增大，整体温度升高。

4.4 干燥带长度对绝缘子温度分布的影响

现分析绝缘子表面干燥带的周向形成过程，由于干区未生成环状干燥带，因此要建立完整的三维模型来进行分析，取干燥区宽度3 mm，位置在下伞盘r=50 mm处，用绕对称轴的角度来表示长度，c为绕对称轴角度，分别取30°，90°，180°，270°。从图10湿污均匀和干燥带产生后绝缘子的温度分布云图可以看出，干燥带形成后会使绝缘子表面温度大幅降低，与沿爬电路径温度分布规律不同，温度最高处集中干燥带区而不是钢脚附近区域。

图10 绝缘子温度分布云图

图11为干燥带周向发展过程中的温度分布云图。由图11可知，出干燥区周向长度对绝缘子表面温度分布的影响，干燥带未形成首尾相接的环时，随着干燥区周向长度的增加，温度呈下降趋势，但温度变化并不大；当干燥区形成环状干燥带时，温度会有大幅度下降。在这个过程中，绝缘子表面干区内部的温度低于同周向上其他位置的温度，但干区两端的温度始终最高，这就造成干区继续延伸最终形成干燥带；经过干区域的径向温度分布与不经过干区的径向温度分布情况有差别，这为红外检测技术提供了参考。

图11 干燥带周向发展过程中绝缘子温度分布云图

通过分析阐明了绝缘子表面出现干燥点后必将形成干燥带的原因。基于图1绝缘子等效电阻模型，假设干燥区出现在图中R11的位置，干燥区出现后，R11阻值迅速增大，使R11上电压降增加，而当干燥区周向增大后在周向上与其并联的一部分电阻R21～Rk1阻值也增大，这就导致R11～Rw1的并联阻值增加，从而在串联电阻中所占比例增大。干燥带角度越大，周向R11～Rw1中并联阻值越大，其上压降也越大。由于干燥带宽度未变化，干燥区上最大场强增加，这表明干燥带周向扩张使得干燥带上最大场强增大，加剧干燥带的产生。

5 结束语

运用有限元分析软件，根据真实绝缘子结构建立三维模型，对湿污绝缘子的温度场分布进行了深入的探讨，得到结论：

a.绝缘子湿污均匀情况，热平衡后钢脚附近温度最高，当绝缘子产生干燥带时，绝缘子相比于湿污均匀情况整体温度下降，最高温度出现在干燥带处。

b.干燥带出现在绝缘子表面不同位置时，绝缘子径向温度分布特征差异较大，并且干燥带越靠近绝缘子边缘时，绝缘子的整体温度越高。

c.随着干燥带宽度增加，绝缘子整体温度下降，并且最高温度附近温度的变化梯度减小。

d.绝缘子下伞盘干燥带条数增加，除了整体温度下降外，径向温度分布曲线变化不大，靠近钢脚处的干燥带温度最高，处于不同侧的干燥带对绝缘子表面温度分布有影响。

e.绝缘子表面出现干燥区但还未生成首尾相接的环状干燥带时，干燥区内部的温度较低，但两端温度始终保持最高，造成干区继续延伸，随着干燥区长度增加绝缘子温度下降，但变化并不大，直到生成首尾相接的干燥带时，温度大幅下降。