一种基于多视角数据融合的网络社区检测算法
马晓峰 耿君锋 范 超
1(中国人民解放军战略支援部队信息工程大学 河南 郑州 450000) 2(国防科技大学信息通信学院 湖南 长沙 410073)
0 引 言
在社交网络中,用户真实社区归属是客观存在的[1],社区检测方法能否获得与客观相符的用户社区归属划分结果既取决于方法的可靠性,又取决于数据的真实性。然而,由于网络用户行为的复杂性,非常可靠并且真实的数据通常是难以获取的,这主要表现在干扰数据、无用数据、矛盾数据等的广泛存在,并且很多情况下还存在用户数据缺失的现象。例如,在Tweets用户交流中,两个用户间存在相互关注关系,但是可能一个用户只听不说,那么该用户的内容特征就为空;同样的,一些用户可能经常发表一些内容来表达自己的观点,但是并不关注其他人或者不添加粉丝等,那么他们就没有链接关系数据。在社交网络中,某些内容属性数据缺失或者链接关系数据缺失的用户广泛存在,这些用户称为孤立节点。孤立节点存在有多种原因,如网络中的“僵尸账号”的存在造成用户链接关系网络十分稀疏,或者用户与其他用户交流数据很少造成节点数据很少等。在数据提取时,由于存在部分孤立节点,因此会形成大量的部分数据集。对于社区检测来讲,如何针对这些缺失数据,实现有效的信息互补,进而获得更好的社区检测结果,是十分有必要的。
与一般数据不全现象相比,这里部分数据集表现在用户某一视角信息全部丢失,而不是丢失某一视角信息中的部分特征数据。目前,许多研究集中于处理数据不全等问题[2-3],但是对于部分数据集的社区检测研究不多。多视角聚类[4]依靠不同视角之间的信息补充提高聚类的性能,由于用户存在多个视角,不同视角之间可以相互补充,这为部分数据集的融合聚类提供了有效的方法。但是,如何有效处理孤立节点,使得算法更加鲁棒,避免因为孤立节点而造成性能的急剧下降,是一个重要的研究内容,特别是在不同视角之间数据质量差异较大的情况下,显得尤为重要。
文献[2]首先研究了包含两个视角的部分数据集聚类问题。在该方法中,数据节点被分为包含每个视角数据的正常数据和只包含一个视角信息的部分数据节点,对于正常数据,仍旧采用NMF(Nonnegative Matrix Factorization)的融合策略进行多视角融合,而对于部分数据节点,则不进行多视角融合,只在单视角内进行数据聚类。其目标函数描述如下:
(1)
s.t.U1≥0U2≥0

在此基础上,文献[5-6]在聚类过程中,对每个视角引入了图正则信息以强化节点的局部结构保持特性。同样的,基于该思想,文献[7]则研究了如何实现算法的“online”处理。文献[8]则建立了针对部分数据集的监督特征提取方法。
在网络社区检测中,可以借鉴多视角聚类的方法研究部分数据集的社区检测问题。一种思想如文献[2]所述,对孤立节点不进行处理;另一种思想是对于孤立节点,通过没有缺失数据的视角,找到该节点的最近邻,利用最近邻节点的特征信息作为该孤立节点的特征,参与到多视角融合当中,从而实现部分数据集的多视角聚类。
1 多视角数据融合社区检测算法
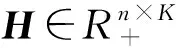
1.1 正则约束项构造
文献[2]利用两个视角的统一低维表示矩阵来构建融合策略,这里仍采用视角之间的差来描述视角之间的融合:
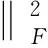
(2)
为了在部分数据集的情况下建立融合正则项,需要引入指示矩阵来加以区分。考虑两种正则约束项。第一种:对于内容属性数据Xn×m,若Xn×m是部分数据集,则可以构造缺失用户指示矩阵MM_C∈n×n,公式如下:
(3)
第二种:考虑多视角数据集,不同视角所描述的社区结构是一致的,可以利用其他视角中该用户的最近邻信息作为该用户的约束信息构造约束项。设Xn×m中用户i没有数据信息,而链接关系矩阵Gn×n中用户i存在链接关系信息,利用CAN(Clustering with Adaptive Neighbors)算法[9]可以找到用户i的最近邻用户j。这里认为用户i与其最近邻j具有最高的相似性,两者的社区信息是一致,故可以构造缺失用户指示矩阵MC∈n×n,公式如下:
(4)
同理,对于链接关系矩阵Gn×n,也可以构造两种缺失用户指示矩阵:MM_L∈n×n和ML∈n×n,公式如下:
(5)
(6)
据此,可以构造两种融合约束正则项如下:
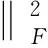
(7)
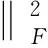
(8)
对于第一种,其表示:对于缺失的用户数据,在融合约束中将其剔除掉,即只考虑对于两种视角的数据都有的用户进行融合,而对于某种视角数据缺失的用户不进行约束;对于第二种,在融合约束时,利用没有缺失数据的最近邻关系来弥补缺失的视角数据信息,即对于内容数据缺失的用户,在进行视角逼近时,利用链接关系数据的最近邻用户的数据代替该用户缺失的数据。
由此构建两种优化目标如下:
(9)
s.t.V≥0,H≥0,SX≥0,SG≥0
(10)
s.t.V≥0,H≥0,SX≥0,SG≥0
1.2 优化目标的求解
优化目标J2可以重新描述为:
αtr(MCHHTMCT-MCHVTMLT-MLVHTMCT+MLVVTMLT)
(11)
引入拉格朗日算子ω1、ω2、ω3、ω4分别约束H≥0,V≥0,SX≥0,SG≥0,则拉格朗日函数L描述为:
L=J2+ω1tr(HT)+ω2tr(VT)+ω3tr(SXT)+ω4tr(SGT)
(12)
L对H、V、SX,SG的一阶导数分别为:
(13)
(14)
(15)
(16)
据KKT条件[10], 令ω1(ij)H(ij)=0,ω2(ij)V(ij)=0,ω3(ij)SX(ij)=0,ω4(ij)SG(ij)=0,则:
同理可求得针对V的KKT条件,整理可得迭代公式:
(17)
(18)
(19)
(20)
综上,经过迭代计算可以获得每个视角的社区指示矩阵H和V,再利用K-近邻分类法的方法将节点归属到相应的社区中去。
算法:基于多视角数据融合和NMF的社区检测算法 输入:链接关系矩阵Gn×n, 属性矩阵Xm×n,参数{θ,α}, 聚类个数K;
输出:聚类指示矩阵H、V;
1 初始化H、V、SX、SG
2 While 迭代次数和优化误差< 阈值do
3 正则化SX、H
4 正则化SG、V
5 更新Hby 式(17)
6 更新SXby 式(18)
7 更新Vby 式(19)
8 更新SGby 式(20)
9 End
10 返回H、V
1.3 算法复杂性分析
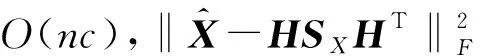
2 实验结果与分析
2.1 数据集与实验设置
实验中用到如下三个数据集:
CiteSeer[11]:该数据集包含3 312个节点和4 732条边,每一个节点代表一篇科技文献,每一条边代表科技文献之间的引用关系,此外每一个节点都关联一个类别属性,社区数为6。
Cora[12]:该数据集也是科技文献引文网络数据集,包含2 708个节点和5 429条边,每一个节点都关联一个类别属性,社区数为7。
WebKB[13]:该数据集由 Cornell、Texas、Washington、Wisconsin等4所大学的网页及网页之间的链接关联关系构成,共分为5个社区。
实验设置如下:
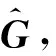
(2) 缺失数据选择:针对内容属性数据X,按照[0, 0.05,0.1, 0.2, 0.3, 0.4, 0.5,]的比例,在所用节点中随机选取若干设置X的行向量为0,分别根据两种不同的约束正则项与链接关系网络进行融合社区检测,统计结果的AC(Accuracy)和NMI(Normalized mutual information)[14];针对链接关系网络cites、inbound和outbound,分别按照上述比例随机选取若干节点,并在这三个网络中随机设置节点的所有链接关系为0。
(3) 正则约束项设置:根据算法的两种正则项生成方法,分别进行实验,最近邻产生方法按照文献[9]的方法进行。
(4) 参数设置:重复10次,取10次的平均值作为最终结果输出。
2.2 结果分析与讨论
如图1所示是当链接关系数据缺失时的融合算法结果。图中,上半部分表示AC值的大小,下半部分表示NMI值的大小。其中“*”表示没有数据缺失时的结果,“Δ”表示没有数据缺失时采用NMF[15]、CAN[9]、谱聚类[16]等方法获得的单视角最好的结果,“▷”表示采用约束2(即最近邻的信息代替缺失数据参加融合约束)时内容数据和链接关系数据融合的结果,“+”表示采用约束1(即缺失数据不参加融合约束)时内容数据和链接关系数据融合的结果。
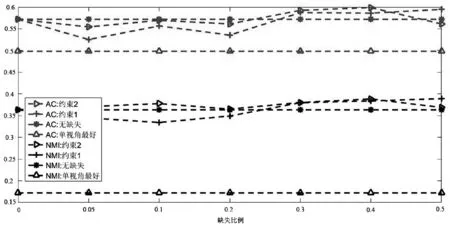
(a) Wisconsin数据集
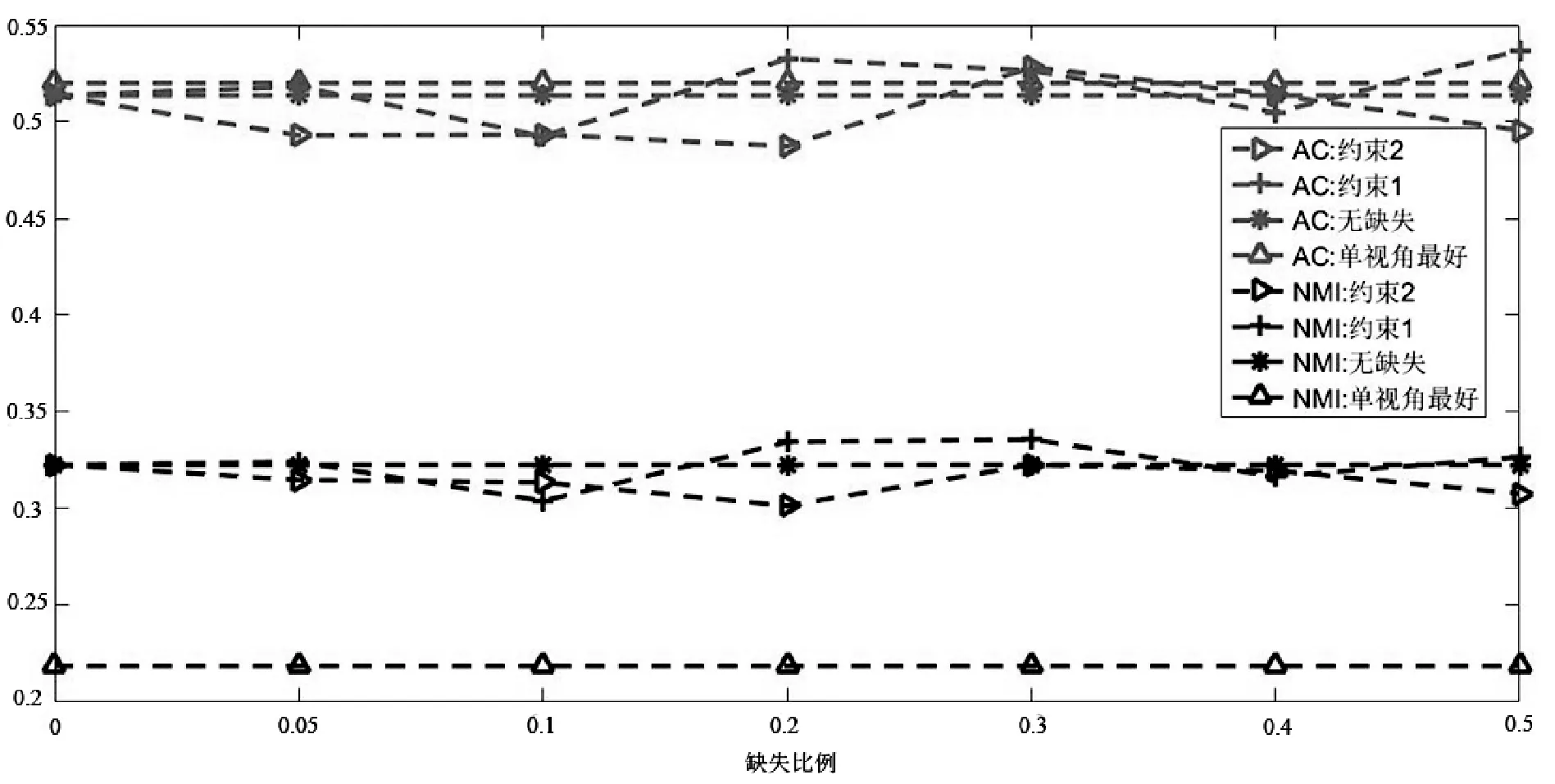
(b) Washington数据集
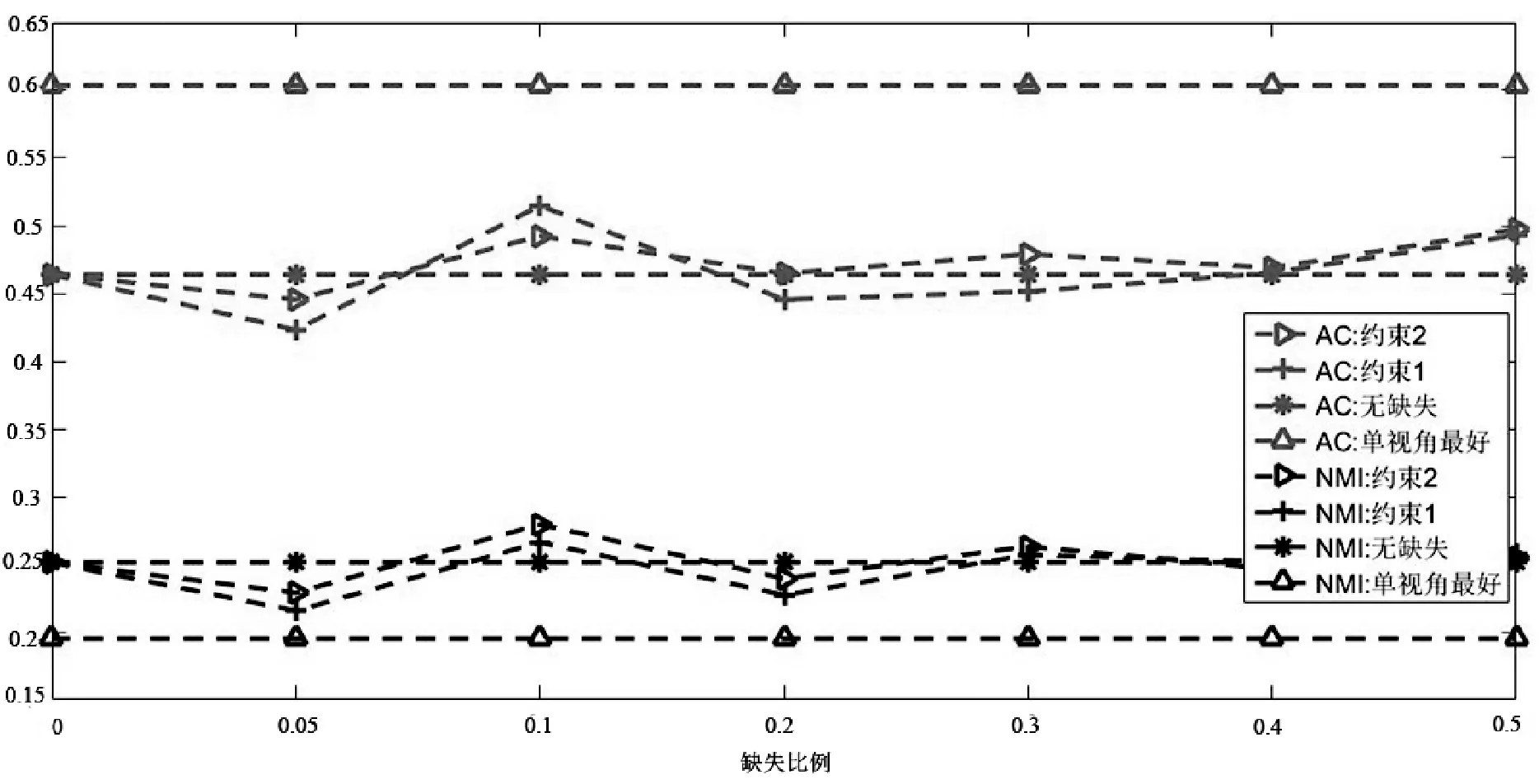
(c) Texas数据集
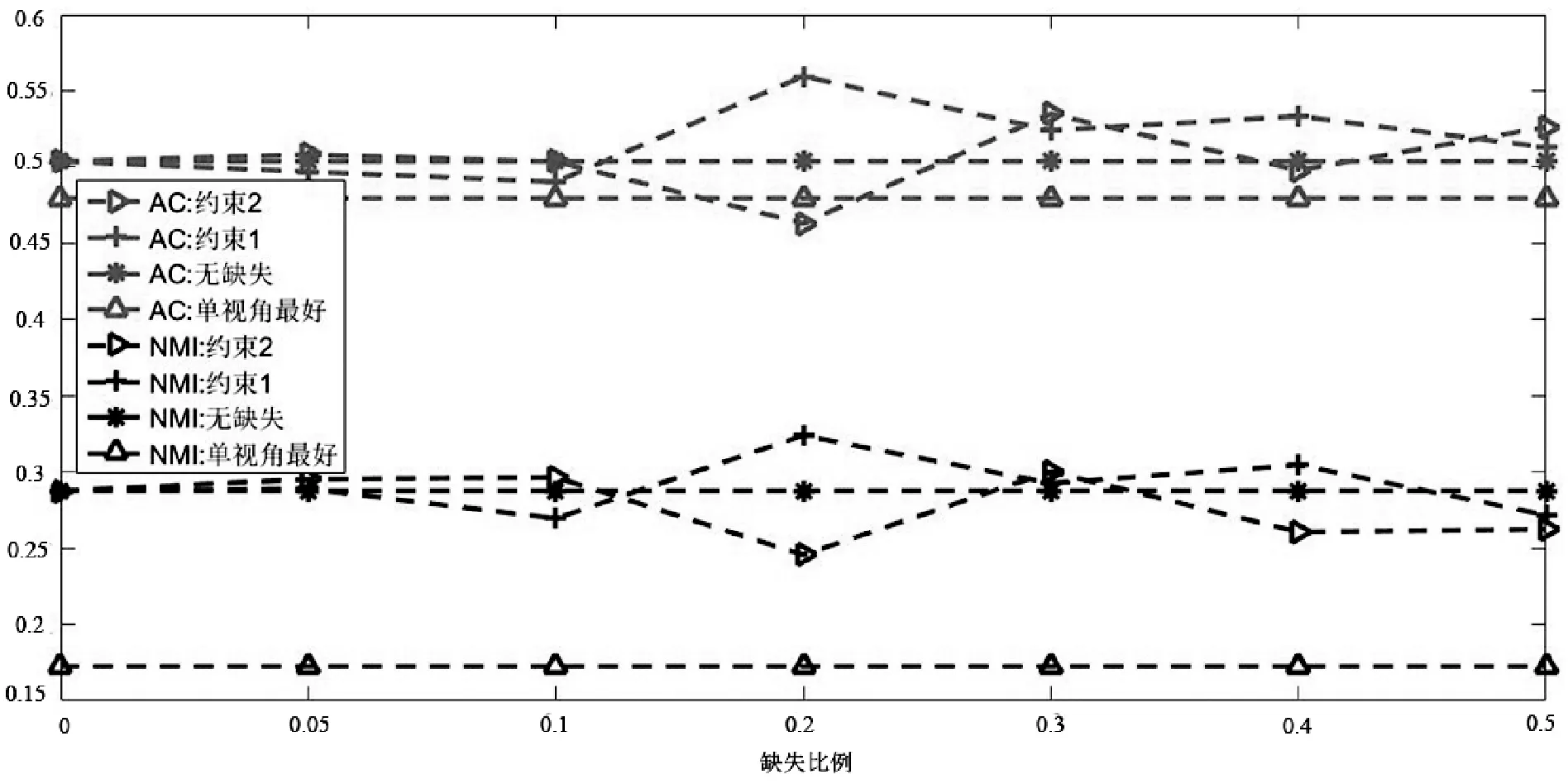
(d) Cornell数据集
(e) Cora数据集
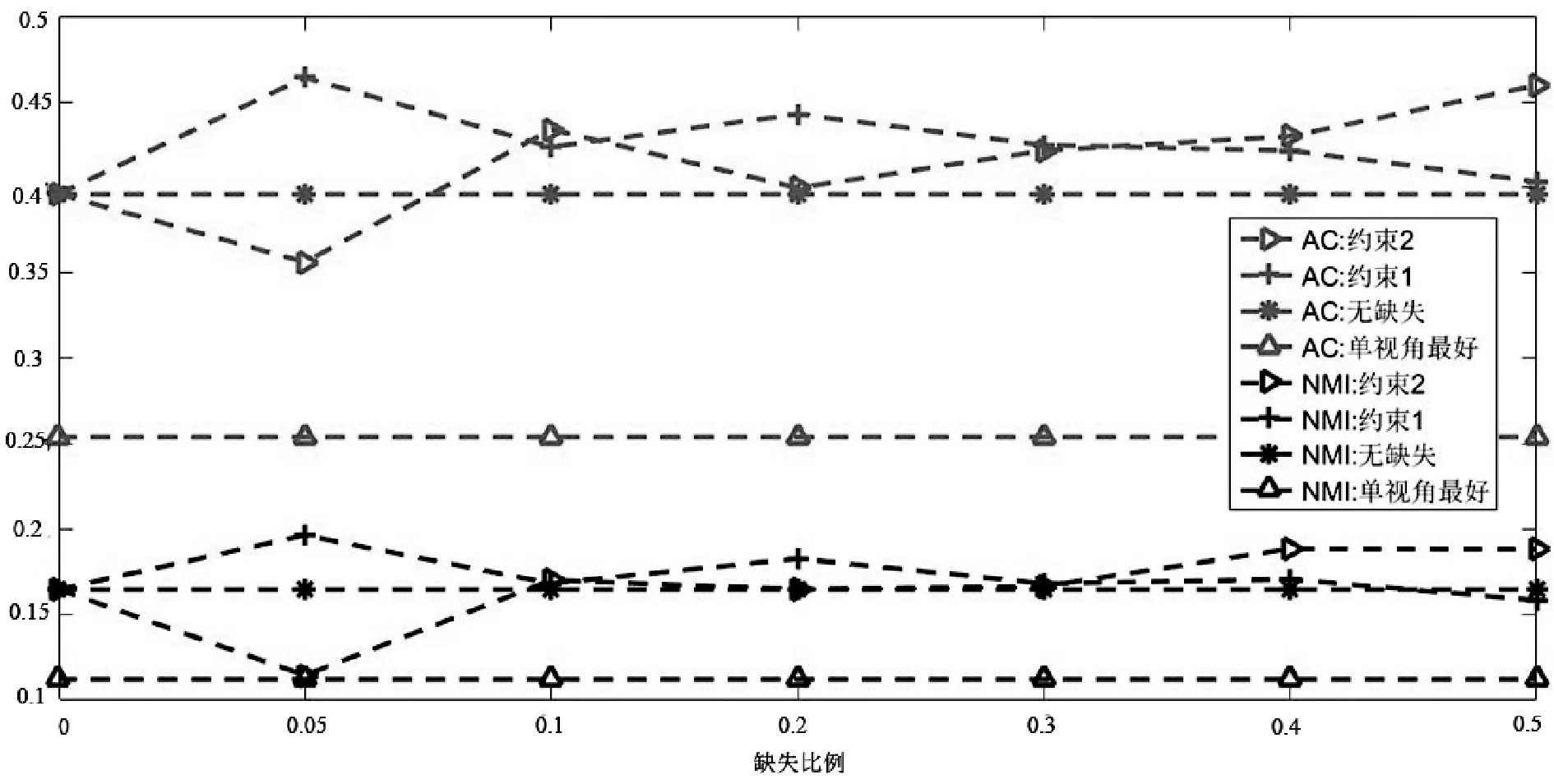
(f) CiteSeer数据集 图1 链接关系数据缺失时不同社区检测算法性能比较
从图1中可以看出:第一,虽然有链接关系数据缺失,但是在Wisconsin、Washington、Cornell和CiteSeer数据集上,融合算法的性能与没有缺失数据时的性能大致相等甚至于略好于它们,这说明:① 社区检测算法中,三个链接关系的融合,可以有效弥补数据缺失带来的信息丢失,保证了社区检测的稳定;② 由于内容属性数据的质量好于链接关系数据,因此减小了链接关系数据的缺失对社区检测结果的影响;③ 部分链接关系数据的缺失客观上也减少了部分错误信息的影响和干扰,因此提高了社区检测结果的精度;④ 两种融合约束项都可以发挥较好的互补效果,在Wisconsin数据集上,约束2要好于约束1,而在Cornell数据集上,约束1要好于约束2。
第二,由于链接关系网络中每个节点的重要性、作用等不尽相同,即节点在网络中的地位是不相等的,因此,随着丢失链接关系数据的用户增加,社区检测的结果并没有随之简单的增加或者减少,如在Wisconsin数据集中,当随机丢失5%、10%的数据时,算法性能略有下降,而当随机丢失30%、40%的数据时,算法的性能略有增加。
第三,在Texas数据集上,虽然融合后的结果在AC值上没有超过谱聚类算法,但是在NMI性能上,算法的结果要好于单视角,并且随着随机数据缺失的 增加,NMI的变化规律也存在上下波动的现象。而在Cora数据集上,在AC和NMI上,融合后的结果没有谱聚类好,但是性能的变化规律与其他数据集相同。
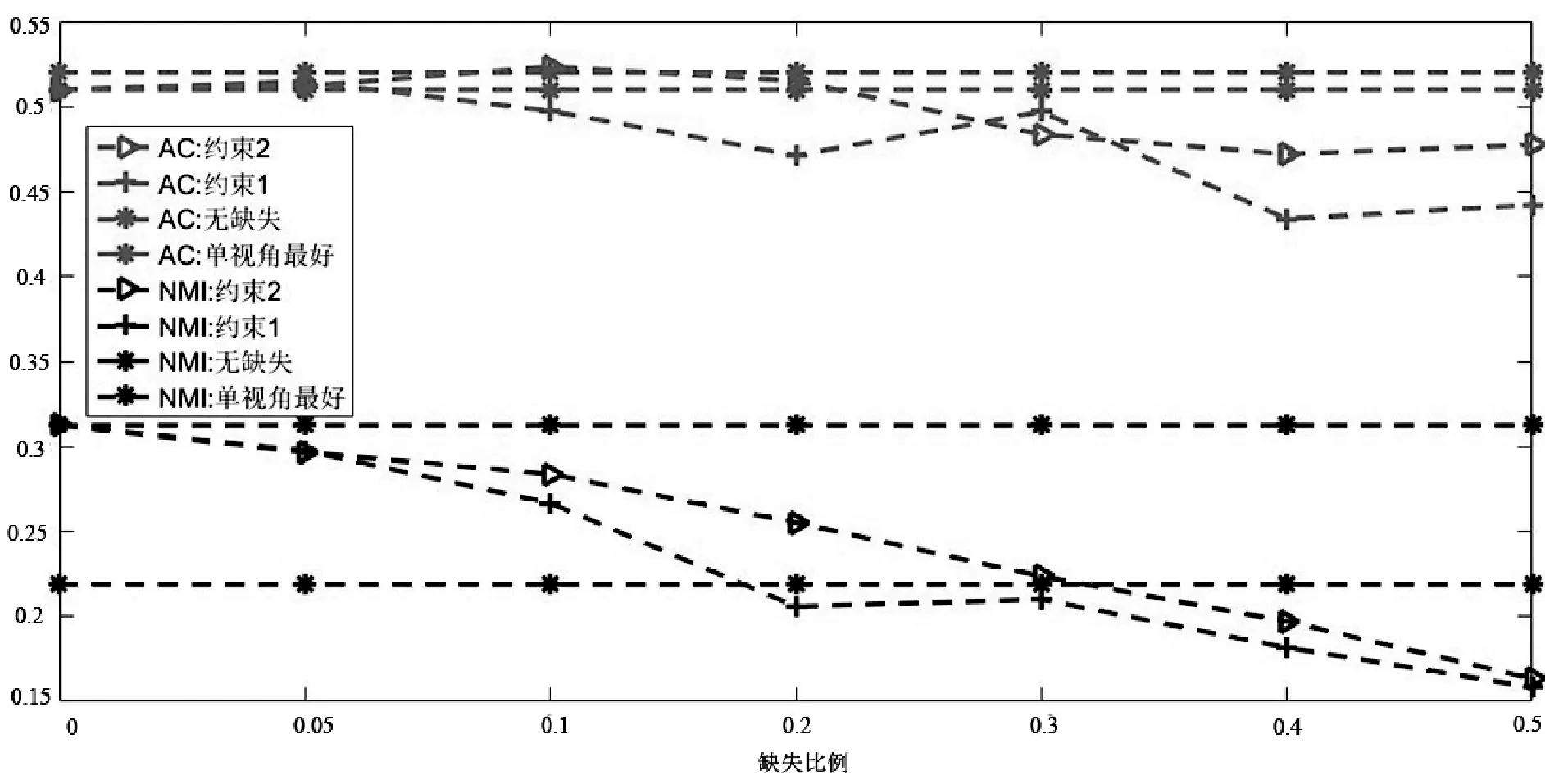
图2所示是当内容数据缺失时的融合算法结果。可以看到,第一,随着缺失数据的增加,算法融合的性能也随之发生显著的有规律的下降,尤其是当缺失数据大于30%时,性能下降明显,这是因为:① 内容数据的数据质量较链接关系数据要好,因此内容数据的缺失对算法性能的影响比较明显;② 内容数据是属性矩阵,用户数据缺失只影响用户自己本身,因此随着缺失数据的增加,算法性能存在有规律的下降,仅在Wisconsin和Cora数据集上,当缺失数据在5%时,融合后的性能好于没有数据缺失时的结果,在其他数据集上,融合后的结果都随之减小。
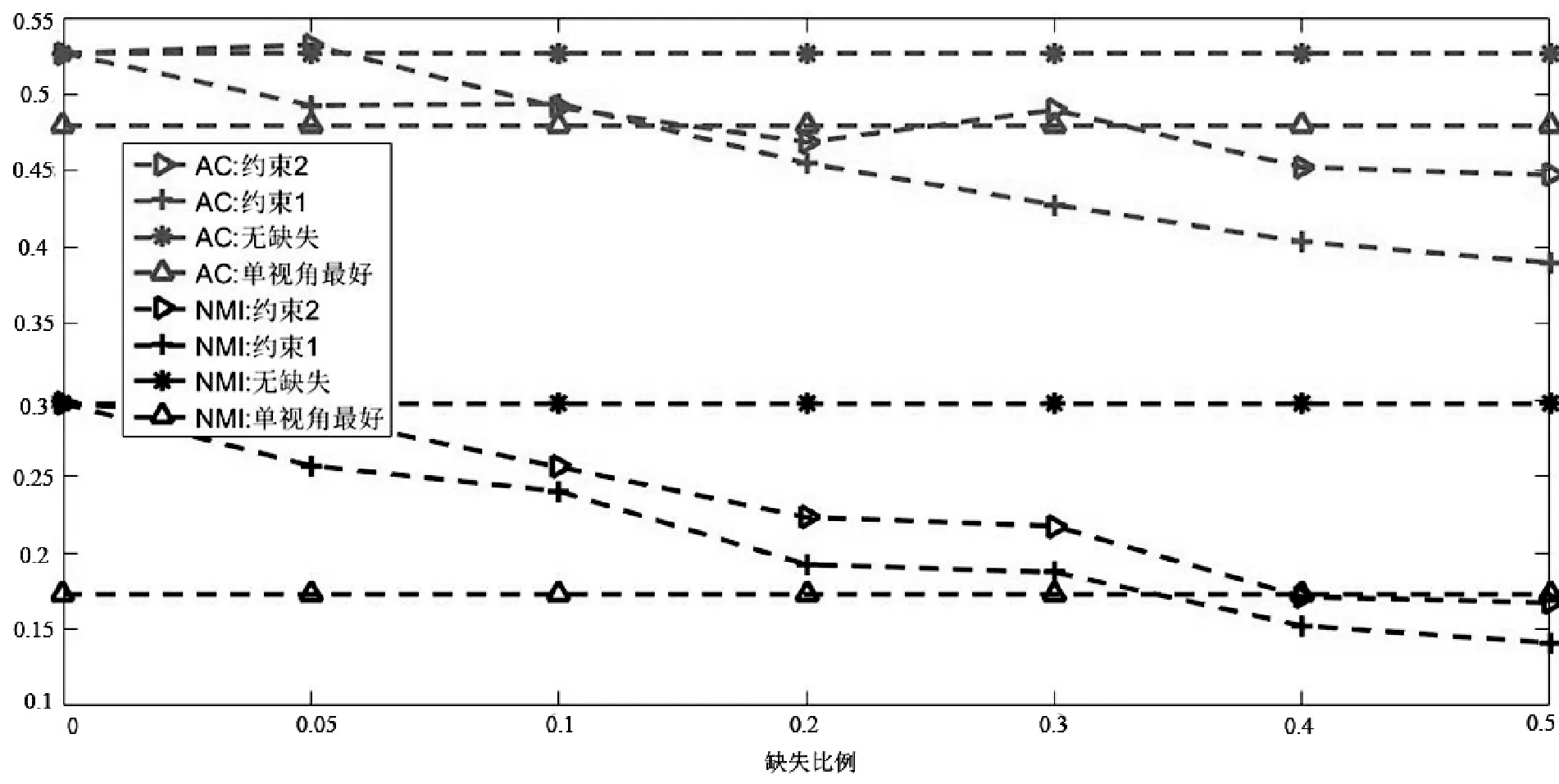
第二,在正则项2和正则项1的约束下,算法融合的性能都随之发生有规律的下降,随着缺失数据的增加,正则项2的性能要略好于正则项1。如在Washington、Cornell、CiteSeer数据集上,当数据缺失40%以上时,正则项2的性能要高于正则项1。
(a) Wisconsin数据集
(b) Washington数据集
(c) Texas数据集
(d) Cornell数据集
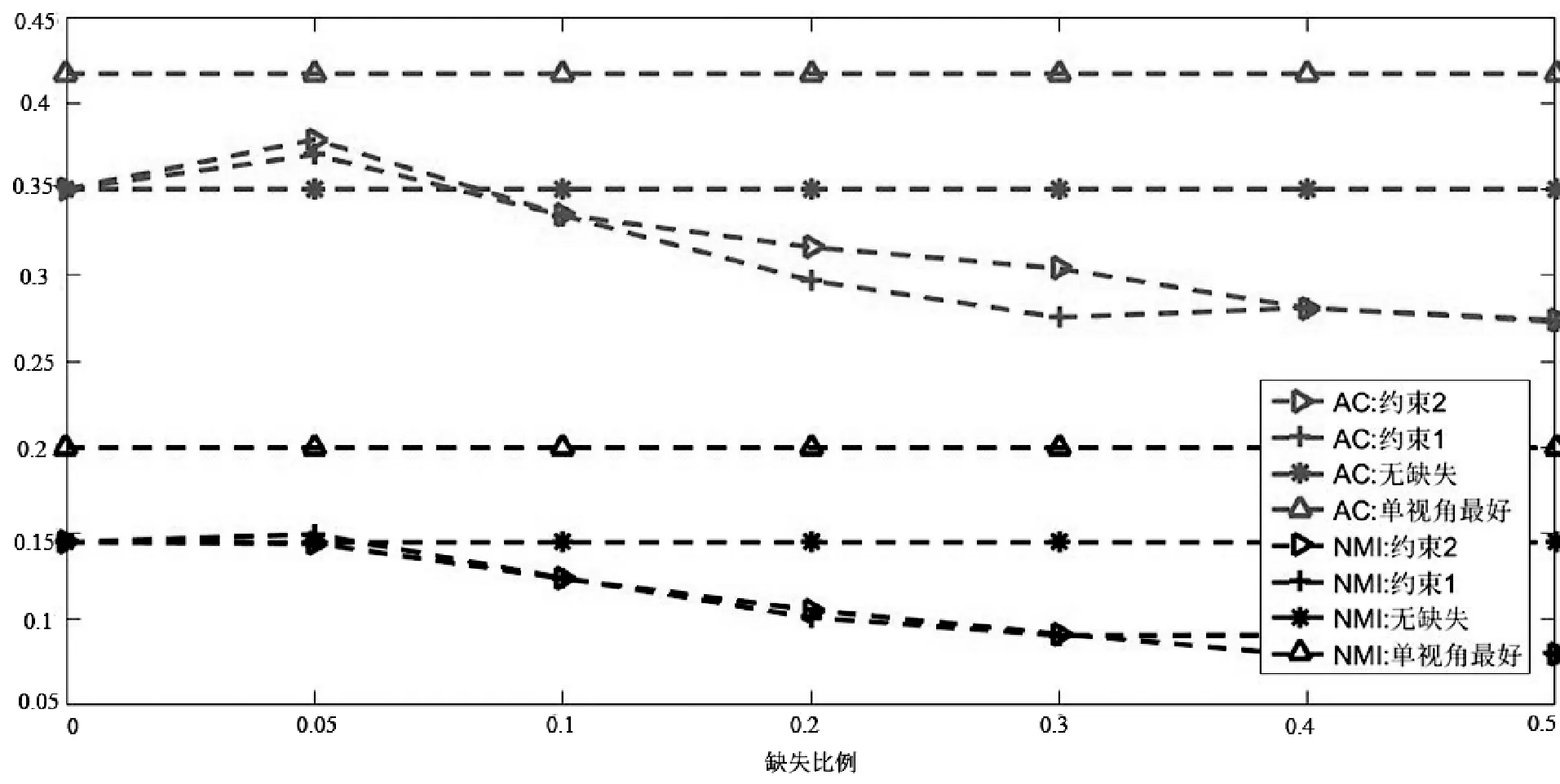
(e) Cora数据集
(f) CiteSeer数据集 图2 内容数据缺失时不同社区检测算法性能比较
比较图1和图2也可以发现,当内容数据质量较好,而链接关系数据质量较差时,链接关系数据的缺失对社区检测结果的影响要小于内容数据的缺失,这也说明,本文提出的算法能够适应数据质量差异大的特点,避免了“1+1<2”的尴尬结果出现,适应性较好。同时也可以看到,由于节点在链接关系网络中所处的地位、作用不同,节点数据的缺失,会造成整个网络结构全局的变化,缺失的数据越多,网络变化越明显,社区检测的结果越敏感,因此,获得真实反映用户结构特点的链接关系网络对于社区检测来说也是非常重要的。
3 结 语
本文对数据缺失情况下的多视角异构社区检测问题进行了讨论,构造了两种处理缺失数据的正则项,并在此基础上提出了基于两种正则项的异构多视角社区检测算法。真实数据集上的实验表明,算法能够适应视角性能差别大、数据缺失的社区检测问题,获得真实、可靠的社区检测结果。

