标准模型下一种高效的基于身份的多签密方案

吴振国，祁正华，王 翔

(南京邮电大学 计算机学院，江苏 南京 210003)

0 引 言

在传统的基于证书的公钥密码系统中，用户的公钥和该用户之间的对应关系通常是由认证中心颁发的证书来绑定的，这种方式会带来复杂的证书管理问题，也就是说用户需要对证书的正确性进行验证，并且存储大量的证书。1984年Shamir[1]提出了基于身份的公钥密码体制，它的基本思想是指由用户的特征信息，如姓名、ID、电话或者其他已知具有用户特征的标识符作为该用户的公钥，使用这种方法不仅解决了基于证书的公钥密码体制中存在的信任问题，而且简化了它的密钥管理程序。Zheng[2]于1997年提出了签密这一新概念，所谓签密就是指将加密和签名合二为一，把消息的保密性和认证性集中在一个逻辑步骤内实现，相比于将两者组合使用的方法具有更高的效率。2006年，Duan等[3]提出了多接收者签密的思想。随着签密问题的关注度不断提高，在此之后有很多国内外学者提出了一些新的签密方案[4-11]，签密算法不断得到创新和完善。

随着信息技术的不断发展，当人们面临一个消息需要经过多个签密者共同签密然后再发送给接收者的问题时，对于多签密方案的研究逐步走进人们的视野。2001年，Mitomi等[12]提出了一种并没有给出其方案安全性证明的多签密方案。张波等[13]于2010年提出了一种新的基于身份的无随机预言机的多签密方案，但通过计算和分析比较得知其方案的计算效率不高。

在张波[13]和李聪[14]等提出的方案的基础上并参考其他有关文献方案，文中提出了一种新的在标准模型下基于身份的多签密方案。通过效率分析，当签密者的人数为n(n>1)时，在签密过程中的幂运算的计算次数比张波[13]和李聪[14]等的方案少了n-1个，并在文中给出了相关安全性的证明。

1 相关基础

1.1 双线性对

设G1,G2分别是一个阶为大素数q的双线性循环群，p是群G1的生成元，称e:G1×G1→G2是一个双线性映射，并且满足以下性质。

(2)非退化性：存在P,Q∈G1，使得e(P,Q)≠1。

(3)可计算性：存在一个有效的算法在多项式时间内计算e(P,Q)。

1.2 困难问题假设

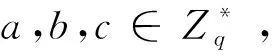
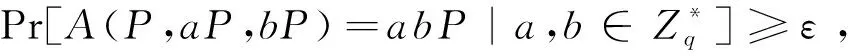
1.3 签密模型

基于身份的多签密方案通常包括四个阶段：

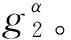
(2)密钥提取阶段(extract)：由PKG将给定用户U的身份IDu生成与之相对应的私钥du，然后通过秘密渠道发给用户U。

(3)多签密阶段(multi-signcrypt)：算法通过多个发送者的私钥dAi、接收者Bob的身份IDB和消息m，生成密文σ。

(4)解签密阶段(unsigncrypt)：该算法由接收者Bob执行，通过输入公开系统参数、自己的私钥dB、多个发送者的身份IDAi以及密文σ，输出明文消息m或者该密文是无效的提示。

2 文中方案

系统建立阶段(setup)：令G、GT是两个双线性循环群，这两个群的阶均为素数q，群的规模由安全参数k决定，g是群G的生成元，双线性映射e：GG→GT。Hu和Hm是两个抵抗碰撞Hash函数，这两个函数的功能是可以将长度任意的身份(ID)和消息(m)映射成文中方案所要求的长度，用符号表示为：Hu：{0,1}*→{0,1}nu，Hm：{0,1}*→{0,1}nm。随机选择α∈Zq，g2∈G，并且计算g1=gα∈G。随机选择u'∈Zq,m'∈G，定义向量Uu=(ui)，其长度为nu，定义向量Mm=(mi)，其长度为nm，其中ui∈RZq，mi∈RG。然后定义ω=e(g1,g2)。最后得到系统公共参数：π={G,GT,e,g,g1,g2,u',Uu,m',Mm,Hu,Hm}；系统主密钥为

密钥提取阶段(extract)：通过Hu函数将用户j的IDj映射成一个长度为nu的比特串，记I[i]是IDj第i位比特，记Uj⊂{1,2,…,nu}为I[i]=1的下标i的集合。PKG随机选择rj∈Zq，然后计算用户j的密钥：

因此，可以计算签密者UAi(i=1,2,…,n)和接收者B的私钥：

多签密阶段(multi-signcryption)：用户u采用类似密钥提取阶段中同样的方法获得Mj集合,即Mj∈{1,2,…,nm}；PKG随机选择ri∈Zp，之后对消息m进行签名。

(1)计算σi1=e(g2,g)ri

(2)σi2=dAi2

(4)将(σi1,σi2,σi3)发送给指定的签密者Cindy，假设Cindy是第j个签密者，则令其选择的随机数为rC，然后计算：

M=Hm(m||ω)

c=m⊕H(ω)

σ2={σi2|i=1,2,…,n}

σ4=grC

最终得到的签密密文为σ=(c,σ1,σ2,σ3,σ4)。

解签密阶段(unsigncrypt)：接收者Bob在收到密文之后，将依照以下算法对密文进行解密：

计算：ω=e(σ4,dB1)；m=c⊕H(ω)；M=H(m‖ω)。

如果下面等式成立，则Bob就接收消息：

3 安全性分析

3.1 正确性

方案的正确性证明如下：

e(σ3,g)=

3.2 安全性

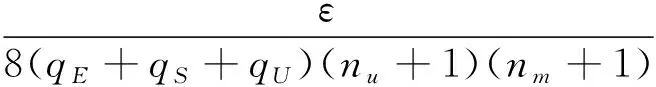
证明：假设挑战者C收到一个实例(g,ga,gb,gc,α∈GT)，该实例是一个随机的DBDH问题，目标是判定α=e(P,P)abc是否成立，C可以将Λ作为子程序调用，文献[15-16]提出的思想作为此方案的证明。

系统参数设置：

挑战者C设置lu=2(qE+qS+qU),lm=2qS。

(1)随机选择2个整数ku和km,其中0≤ku≤nu,0≤km≤nm；

(2)随机选择一个整数x'∈Zlu，一个nu维向量X=(xi),xi∈Zlu；

(3)随机选择一个整数z'∈Zlm，一个一维向量Z=(zi),zi∈Zlm；

(4)随机选择2个整数y',w'∈Zq，一个nu维向量Y=(yi),yi∈Zq和一个nm维向量W=(wi),wi∈Zq。

为了便于分析，对消息u和消息m定义如下函数：

挑战者构造参数：

g1=ga,g2=gb

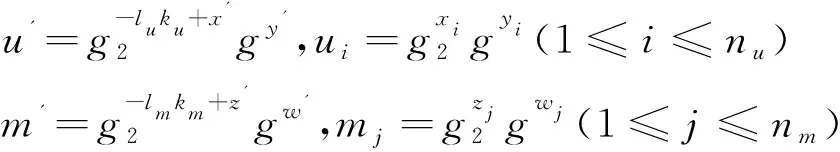
阶段1：挑战者C回答敌手Λ的询问。

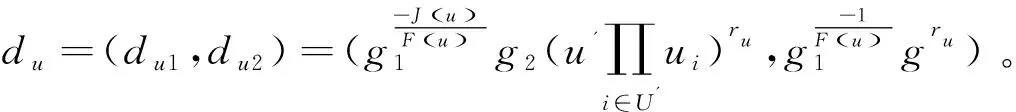
由F(u)=0modq，得F(u)=0modlu；由F(u)≠0modlu，得到F(u)≠0modq。

只有当F(u)≠0modlu不等式成立时，挑战者C才能够成功模拟这样一个私钥。

(2)多签密询问：敌手Λ随时都能够对明文m，每个签密者的身份IDA1,IDA2,…,IDAn以及接收者的身份IDB进行询问，然后对F(uAi)≠0modlu进行判断，若不等式成立就按照密钥询问算法产生关于身份uAi的密钥，再通过运行算法Multi-Signcrypt(m,dA1,dA2,…,dAn,IDB)来对Λ的询问进行应答。

(3)解签密询问：敌手Λ随手都能够对密文σ进行解签密询问。然后对F(uB)≠0modlu进行判断，若不等式成立，就按照密钥提取算法产生身份uB的密钥，然后通过运行算法Unsigncrypt(σ,dB,IDA1,IDA2,…,IDAn)来应答Λ的询问。

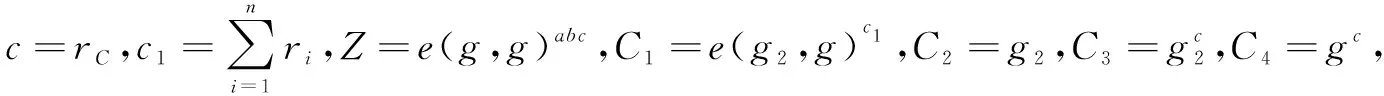
模拟游戏成功。

猜测：最后，敌手Λ给出了猜测b'，其中b'∈{0,1}。若b'=b，则敌手Λ赢得了游戏。

根据上述过程，达到下面4个条件才能模拟成功：

(1)在密钥询问过程中须满足F(u)≠0modlu。

(2)多签密询问中满足F(ui)≠0modlu,i∈[1,n]。

(3)在解签密询问中须满足F(uB)≠0modlu。

为了清晰地表达，假设qI≤qE+qS+qU，定义：

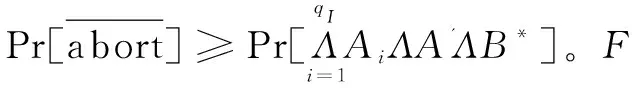
Pr[A']=Pr[F(u*)=0modp]=Pr[F(u*)=

0modlu]·Pr[F(u*)=

0modp|F(u*)=0modlu]=

另一方面，对于任意i,Ai和A'也是相互独立。

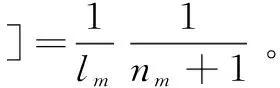
结合以上这些结果，可以得到：

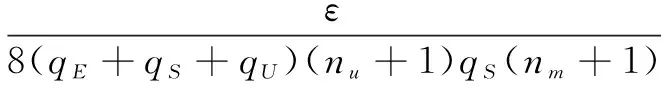
定理2：在CDH困难问题的假设前提下，提出新的多签密方案满足在适应性选择消息攻击下存在不可伪造性。

证明：假设存在一个伪造者Λ能够成功伪造一个有效的签密密文，那么可以通过Λ来构造一个挑战者C，然后使挑战者C来解决CDH问题。挑战者可以通过使用证明密文不可区分性中参数设定的方法来设定公共参数，即C设定g1=ga,g2=gb。

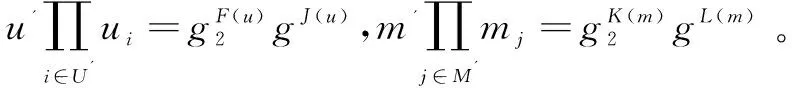
3.3 效率分析

将文中方案与文献[4]和文献[13]中的算法进行分析比较，计算效率方面主要考虑计算消耗比较大的运算，主要有双线性对运算、幂运算以及数乘运算。为便于分析，将这三种运算分别用P,E和M表示。通过计算分析可知，签密者为1人时，文中方案的效率同文献[13]一致，但当签密者的人数大于1时，文中方案的效率更高并且计算规模也相对减小。具体的对比数据如表1所示。

4 结束语

通过对以往提出的多签密方案的研究，在效率方面进行分析并改进，提出了新的标准模型下基于身份的多签密方案，并且证明新方案具有不可区分性和不可伪造性。该方案在多个签密者的情况下，减少了其签密过程中的多个幂运算，同时降低了计算的规模，从而进一步提高了签密的效率。对于密文长度的缩短和运算规模以及通信开销的减小，将会在今后的工作中继续深入研究。