武广高速铁路列车晚点恢复时间预测的随机森林模型

黄 平， 彭其渊， 文 超， 杨宇翔

(1. 西南交通大学 交通运输与物流学院， 四川 成都 610031； 2.综合交通运输智能化国家地方联合工程实验室， 四川 成都 610031；3. 滑铁卢大学 铁路研究中心， 滑铁卢 N2L3G1； 4. 亚琛工业大学 交通科学研究所， 亚琛 52074)

高速铁路高安全性、高速度、高密度的优势使我国高速铁路在短短的八年多时间里，发展成为世界上高速铁路最发达的国家之一。截至2017年，我国高速铁路运营里程超过2.5万km，每日开行的高速动车组旅客列车数占到了全部旅客列车数的65%以上。高速铁路的建设运营，在提升铁路路网规模与质量、缓解运输能力紧张、提高铁路运输服务质量等方面均取得了显著效果[1]。

列车在运行过程中受到来自铁路系统内外的各类因素干扰而晚点，从而降低正点率和运输服务质量。瑞士铁路联盟2011—2015年的统计数据显示，其铁路正点率仅为88%(晚点超过3 min记为晚点列车)[2]。中国铁路总公司的相关统计数据显示，虽然我国高速铁路2015年的始发正点率达到了98.8%、终到正点率达到95.4%，但我国高速列车的运行正点率也只有90%。

列车晚点常被分为初始晚点和连带晚点两类[3]，其中本文所研究的初始晚点按照来源不同又可分为两种情况：

(1) 由于设备故障、交通事故、自然环境等外部因素造成的晚点，称为外因引起的初始晚点。

(2) 由于其他列车连带影响造成的晚点，其对于前行列车而言是连带晚点，而对于被影响的后行列车而言则是初始晚点。

列车运行图吸收晚点的能力是运行图编制质量评价的重要指标，列车运行图弹性被认为是描述和度量晚点吸收和恢复能力的重要评判标准[4-5]。对于晚点恢复模型的研究，计算机仿真方法被认为是建立连带晚点恢复模型的有效方法[6]。Yuan等[7]建立了晚点在车站传播的随机理论模型，用于估计连带晚点的影响及由于进路冲突和接续晚点造成的影响，模型考虑了晚点列车在车站及区间的恢复参数。Meester[8]初步建立了列车晚点传播模型，并指出连带晚点的分布可以从初始晚点的分布推导。 在基于运行实绩数据研究列车晚点恢复问题方面，Hansen[9]基于离线历史数据建立了晚点传播模型，用于检测径路冲突和调度决策问题，但该模型并没有针对晚点恢复问题进行细致研究。Wallander[10]运用数据驱动方法，基于芬兰旅客列车的运行数据建立了晚点链，但其仅仅有1个月的运行数据。Khadilkar[11]基于印度铁路的实际数据计算得到了每列车的平均恢复时间为0.13 min/km，且该数据太过粗略，并不能反映列车在各站、各区间的恢复能力。

从已有研究分析来看，基于列车运行实绩进行高速铁路运输组织的相关问题的研究严重缺乏，但这些研究均指出基于高速铁路列车运行实绩数据对于运输组织优化问题具有重要的作用。Ma等[12]基于高速铁路运行数据开发并初步应用了一套优于传统理论模型的智能系统，该系统具备更优的晚点检测功能。刘健等[13]以京沪高速铁路实绩数据为基础进行列车运行仿真，得到了突发事件的发生概率。庄河等[14]及 Xu等[15]均基于我国高速铁路列车运行数据分析了晚点的分布函数，但其研究只能得到相应的晚点时长概率分布规律，并不能对列车在将来时刻的晚点时间进行定量预测。

本文所研究的晚点恢复时间是指高速列车初始晚点时长与列车到达终到站或从分界站交出时车站到达晚点时间的差值，它等于晚点列车晚点后在其剩余运行里程中所利用的所有恢复时间之和。在晚点发生后，该晚点能否恢复、恢复能力有多强，是铁路部门及旅客非常关注的问题，直接影响到了后续的列车运行组织和旅客的出行计划安排。已有研究多以列车运行图优化为目标，偏重优化理论方面，在指导调度员决策方面略显不足，对基于数据进行高速铁路列车运行晚点恢复理论和方法的研究尚待进一步加强。研究高速铁路的晚点恢复模型，预测高速列车在一定初始晚点水平、运行图结构下的晚点恢复情况，能够使调度员较为准确地估计列车的运行情况，制定合理的行车指挥决策并指导客运及其他相关部门协同完成运输任务，在提高铁路行车指挥质量方面具有一定的实践意义。本文基于武广高速铁路列车运行实绩数据，分析高速列车初始晚点恢复的影响因素，建立了初始晚点恢复的随机森林模型，模型检验表明其具有很好的数据拟合及预测效果。本文的主要立足点主要是通过晚点恢复时间的预测，为调度员提供较为简单直观的决策依据，直接服务于行车指挥实践。

1 问题及数据描述

1.1 问题描述

高速列车运行过程是一个动态的过程，列车将受到来自各方面的干扰而晚点。在运行实际中，调度员将依据调度规则及经验，运用缓冲时间恢复晚点。图1中3条折线分别表示从列车运行实绩中获取的3列车的初始晚点恢复过程，这3列车均在广州北站发生了初始晚点，折线上的各点分别为列车在各站的到达晚点时间，单位为分钟。以G6014为例，该列车在广州北站延误了20 min、在清远—英德西区间恢复1 min、在英德西—韶关区间恢复1 min、在郴州西—耒阳西区间恢复5 min、在株洲西—长山南区间恢复4 min。总的来说，G6014列车在全程利用了11 min缓冲时间来恢复初始晚点，其他列车的晚点恢复过程与G6014类似。

本研究只针对如图1所示的列车(即晚点发生后在后续运行中晚点不再增加的列车，晚点发生后在后续运行中受到二次或多次干扰导致晚点后续增加的情况不考虑在内)。基于武广高铁列车运行实绩数据建立晚点恢复模型来描述高速列车晚点的恢复过程，并最终用于晚点恢复的预测，从而为高速铁路行车组织提供决策辅助及理论依据。

1.2 数据描述

本文的列车运行实绩数据来源于广铁集团所管辖的京广高速铁路南段(武广高速铁路)，武广高速铁路全长1 069 km，共设18个车站。所有列车运行实绩数据均从广铁集团高铁调度所CTCS系统获得，包括上行线广铁集团管辖的武广高铁广州北站至赤壁北站共14个车站、13个区间的所有晚点列车记录，时间跨度为2015年2月24日到2015年12月22日。该数据记录了列车车次、车站、每次列车在每个车站的图定与实际到发通过时刻、最高列车运行速度、每日行车量、以及行车间隔等，部分数据见表1。

表1 原始数据表

由于上下行列车运行图冗余时间分布不同而需分开考虑，因此本文只考虑上行列车运行实绩数据建模，上行方向总共开行列车29 662列列车。下行方向的建模方法相同。

2 初始晚点恢复的随机森林模型

2.1 随机森林模型概述

随机森林是一个由多个树分类器{h(x,βk),k=1,2，…}构成的现代机器学习算法，可以处理大量且多维度的复杂数据，并且对变量间的共线性不敏感，被誉为当前最好的数据挖掘算法之一。其中每一棵树是采用CART(Classification and Regression Tree)算法构建的没有剪枝的决策树[16]。x为输入变量，βk为独立同分布的随机向量，其决定了单棵树的生长过程。随机森林可用于分类与回归，本文基于高速列车运行实绩建立初始晚点恢复的回归模型，探明影响恢复过程的各因素与恢复时间的关系。

随机森林可以理解为由多棵决策树组成的森林，每个训练样本需要经过每棵树进行预测，然后根据所有决策树的预测结果最后来决定整个森林的预测结果。森林中每一棵树都是二叉树，其生成遵循自上而下的递分原则，即从根节点开始依次对训练集进行划分。在二叉树中，根节点包含全部的训练集数据，按照节点不纯度最小原则，分裂为左节点和右节点，他们分别包含训练集的一个子集，按照同样的原则，节点继续分裂，直到满足分支停止规则而停止生长。

2.2 模型参数选择

初始晚点的时间大小将直接影响其影响的程度，对于晚点恢复的要求也各不相同，如20 min的初始晚点与10 min的初始晚点相比，若要恢复正点，20 min的初始晚点需要利用更多的缓冲时间。初始晚点时间越长，对路网列车运行产生的影响一般越大，对晚点恢复的影响也越大。因此，本文首先考虑将列车在初始晚点站的晚点时间(PD)作为第一个自变量。

列车在运行全过程是一个非常复杂的过程，由于受限于更为详细的实际闭塞分区占用及解锁以及车站进路等数据的采集，本文考虑到在列车运行图基本结构不变的情况下各列车的进路及到发线使用、闭塞分区占用和解锁过程均基本不变，转而可以通过分析高速列车在运行时刻、作业时间上的历史表现来近似体现上述作业过程，并作为晚点恢复预测的相关输入参数及条件。

运行图中预留的车站和区间缓冲时间是调度员进行列车运行调整和使列车晚点恢复的资源，能够在一定程度上吸收由于列车运行过程中受到随机因素干扰而导致的晚点时间[17]。本文基于高速铁路列车运行实绩数据，统计了各车站、区间的晚点恢复率见表2、表3。

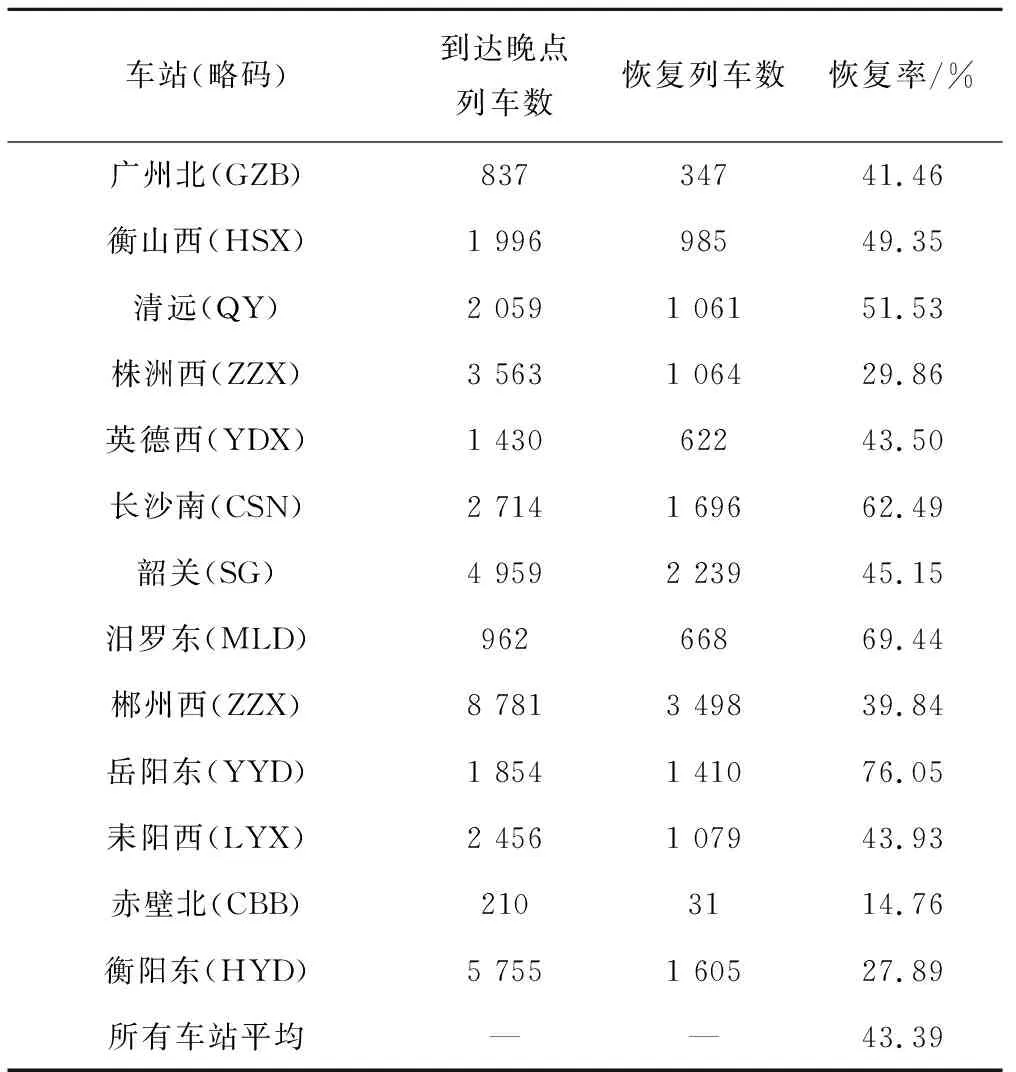
表2 各站晚点恢复率

表3 各区间晚点恢复率

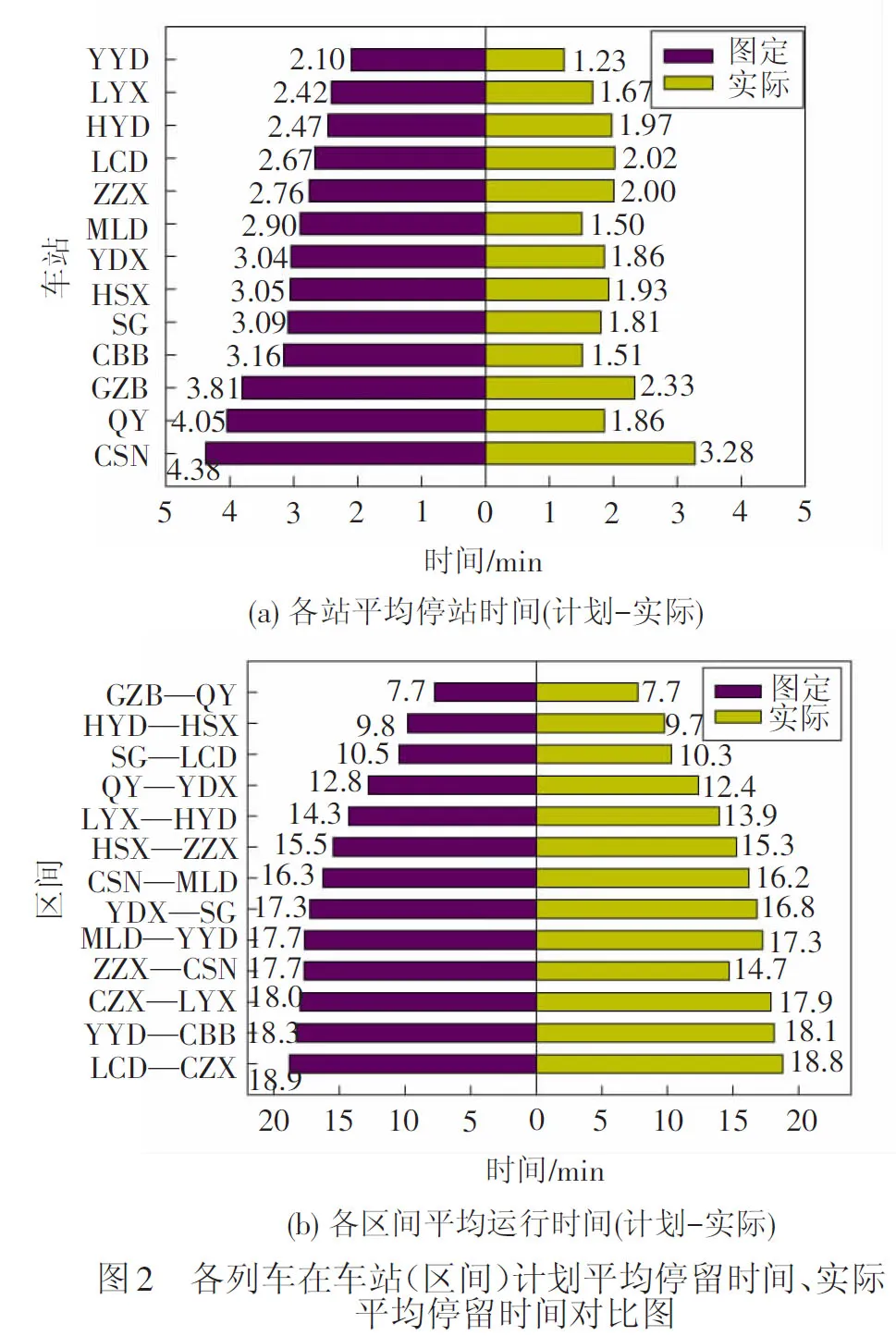
表2、表3数据显示：平均有43.39%的到达晚点列车在车站缓冲时间作用下能得到一定程度的晚点恢复，而平均有42.44%的出发晚点列车能够在其下一个区间在缓冲时间作用下得到一定程度的晚点恢复。更进一步，计算得到了各列车在车站(区间)的计划平均停留时间、实际平均停留时间对比，见图2。从图2可以看出：(1)武广高速铁路列车在车站获得的晚点恢复时间比区间的多，车站缓冲时间的作用要明显于区间缓冲时间；(2)株洲西—长沙南区间的缓冲时间利用远远大于其他区间，平均利用缓冲时间达到了3 min。因此，列车晚点后经停各站的总停站缓冲时间(TD)和所经过区间的总区间缓冲时间(RB)将是影响初始晚点恢复的关键因素，把TD与RB也作为本文的自变量。另外，由于株洲西—长沙南的平均缓冲时间利用值特别大，列车如果以晚点状态通过该区间将可能获得较大幅度的晚点恢复，因此本文引入一个0-1变量(ZC)标识列车是否晚点状态通过该区间。TD及RB的计算式为

( 1 )

( 2 )

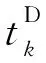
( 3 )

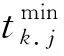
最终，本文选择PD、TD、RB、ZC作为回归模型的自变量，晚点恢复时间(RT)作为模型的因变量，建立高速列车初始晚点恢复的随机森林回归模型。表4所示为用于建模的高速列车运行实绩数据示例，以2015年2月24日的G554列车为例，该列车在郴州西站发生15 min的初始晚点，其在后续运行里程中的总停站时间为10 min、区间总缓冲时间为47 min、其晚点状态经过株洲西—长沙南区间，该列车到达交出站赤壁北时恢复正点运行。

表4 建模数据示例

2.3 各变量关系分析

由于过小的初始晚点时间可能在晚点发生的车站或者临近区间直接被缓冲时间吸收，晚点持续过程较短，因此本文提取了初始晚点时间大于4 min的2 653列列车作为研究对象，并且删除在晚点运行过程中受到二次或多次干扰导致列车晚点增加的列车，对数据进行降噪等预处理操作后，剩余用于建模的数据样本量为917。所有样本按照模型自变量和因变量属性的分布见图3。

图3结果表明提取的各变量值都不服从传统统计模型的变量高斯分布假设， 自变量PD、TD以及因变量RT都是明显的右偏分布，而RB为左偏分布。

图4为各连续变量的散点矩阵图，表5为各变量偏相关系数表，从图4的散点分布以及红色线条以及表5的偏相关系数都可以看出因变量(RT)与各自变量PD、TD、RB都有着比较难以确定的复杂关系；同时各自变量之间却有着可能的线性关系，如TD与RB之间可能存在线性关系。以上各变量分布情况以及变量之间的关系情况表明因变量与各自变量之间的关系较为复杂，若建立传统的统计学模型(如多元线性模型)将不能完整的描述变量之间的复杂关系，模型用于列车晚点时间的预测精度将会较低。因此，本文考虑利用能够解决复杂关系的机器学习模型来建立列车晚点恢复模型。

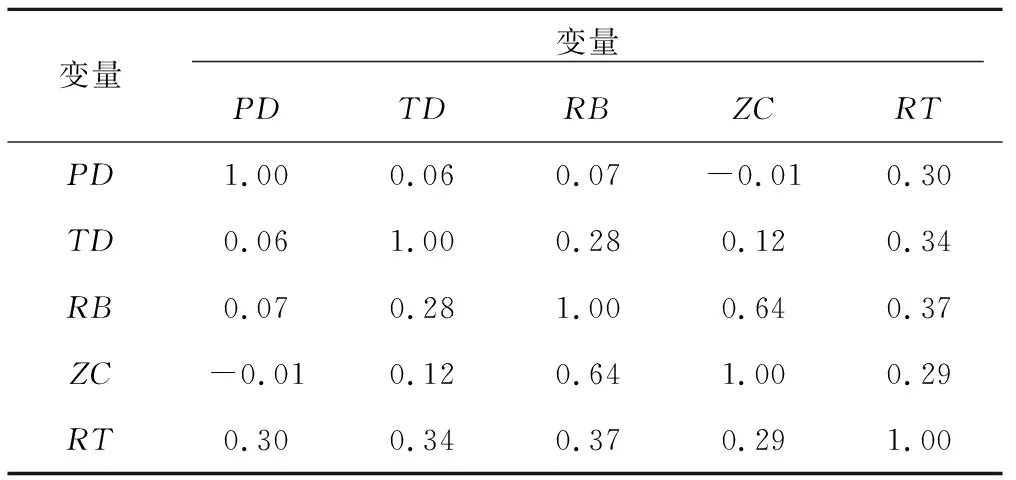
表5 各变量偏相关系数

2.4 模型训练集确定

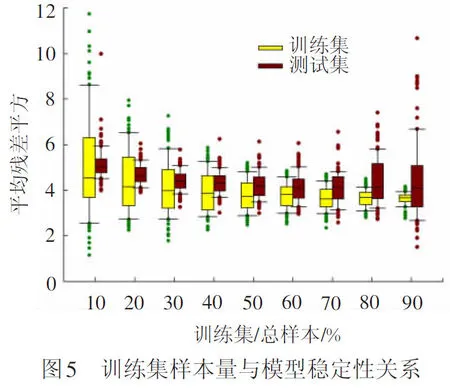
随机森林是典型的采用Bagging技术的多分类模型，对于森林里的每一棵树采用自助法(Bootstrap)随机抽样技术，从总样本集N中有放回地重复随机抽取一定量的训练集生成训练集合，然后根据自助样本集生成k个决策树组成森林，未被抽到的样本集叫做“袋外数据”OOB(Out-of-bag)作为测试集用于模型的测试[18]。训练集的样本量直接影响了模型的稳定性和拟合效果，而测试集的测试效果直接反映了模型的预测精度，在构建模型之前需要确定合理的训练集和测试集样本量。为此，本文分别用不同的数据量来构建模型，每个比例数据量下分别运行100次，得到数据量与模型稳定性及拟合效果的关系图，见图5。对于模型训练集残差平方平均值的分布越集中表明模型越稳定，对于模型测试集，预测残差平方的平均分布越集中表明模型用于预测越稳定。图5表明：当每次抽取的训练集样本较少时，误差分布较离散，模型的稳定性较差；同时，由于训练集较少时测试集较多，因此，测试集残差分布较为稳定；随着选取训练集样本量的增加，模型稳定性明显提高，且训练集和测试集误差都有减小的趋势；但随着模型选取的训练集达到80%，模型测试集预测结果的残差分布较分散，模型的预测效果不理想。基于以上分析，本文最终选择用70%数据量用于模型建立，剩余30%样本作为测试集数据，用于模型有效性检验和预测，这样既能保证模型有较高的稳定性，又能使得有足够的测试数据集且有较好的预测效果。

2.5 模型建立

随机森林模型计算精度及预测能力主要决定于两个主要参数：

(1) 宏观参数：森林的规模，即随机森林里决策树的数量。森林的规模越大，模型的拟合及预测结果越稳定，但计算机运行时间也越长。

(2) 微观参数：每一棵树的计算精度，受到每棵树节点数和每个节点的预选变量数的影响，其决定了单棵树的生长情况，即单棵树的拟合效果与预测能力，需要找到合理的预选变量个数，使模型残差(即模型的损失函数取到最小值)最小，模型损失函数计算式为

( 4 )

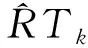
本文利用R语言编程建立随机森林模型，并对模型的两个参数进行优化。

(1) 宏观参数确定

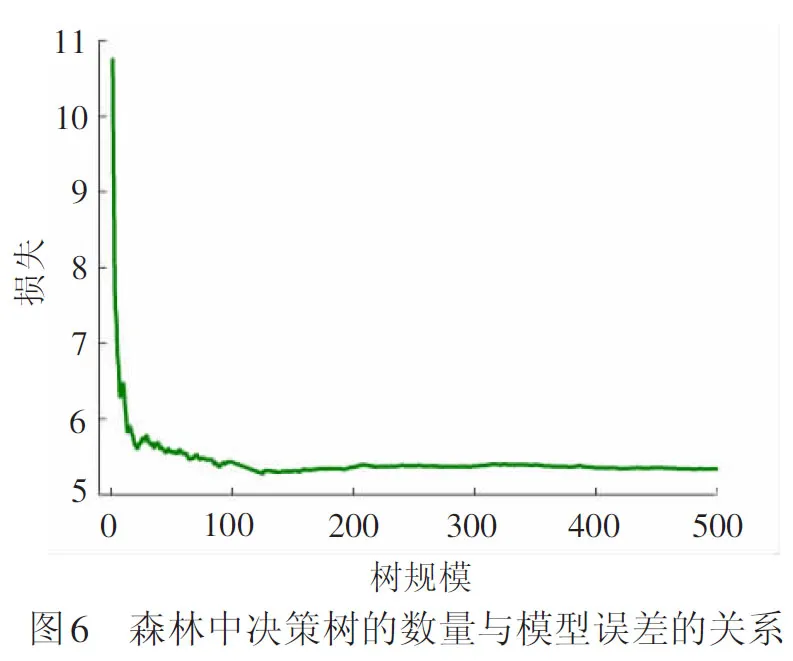
为了确定合理的森林规模，我们研究了森林规模在[1,500]区间对应的模型误差，见图6。随机森林模型中树的个数小于100时误差波动较大，当森林规模大于100后误差较小且比较稳定，最终确定最优森林规模为125时模型误差达到最小。

(2) 微观参数确定

本模型参与建立随机森林模型的自变量有4个，为了确定节点处应随机选取的变量数，分别计算出节点处所选变量为1、2、3、4时对应的模型误差。见图7，当每个节点的预选变量数为2时，模型的平均拟合误差最小，为4.629。

每棵树的分类强度越大，即树枝越茂盛，则模型整体的分类性能越好，图8为随机森林里每棵树的节点数分布，由图可知每棵树的节点数落在区间[37,67]，足见树的结构较复杂，分类能力较强。

因此，最终确定森林规模为125，节点处预选变量为2，模型达到误差最小为4.629。

随机森林通常没有固定的函数模型表达式，R软件“randomforest”包建立的随机森林模型能够自动输出模型自变量的重要度系数见表6，提供了判断各个变量对于建立模型重要性的信息。从表6可以看出：自变量PD系数最大，说明其对随机森林回归模型的贡献最大，其次是TD、RB，0-1变量(ZC)对模型的影响最小。

表6 变量重要度系数表

通过分析模型训练集数据的残差见图9，可以看出，绝大多数的模型预测值与真实列车运行晚点恢复记录的偏差为0，说明模型对测试集数据的拟合效果非常好。

3 模型预测精度及评估

3.1 模型预测精度分析

虽然随机森林模型建立过程中利用袋外数据进行预测，为了进一步验证模型的预测能力，本文利用余下的30%的数据进行模型的预测能力验证，275个测试数据的预测结果见图10。

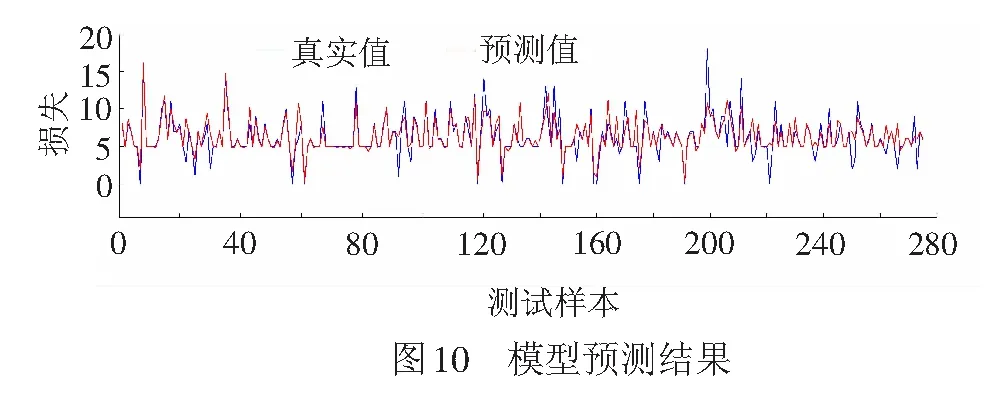
模型的预测精度见图11。从两图的结果可以看出：随机森林模型的预测精度在1 min允许的误差情况下能达到80%，当允许误差为3 min时预测精度超过了90%，且模型的预测误差最大为8 min，可见模型的预测效果非常好。

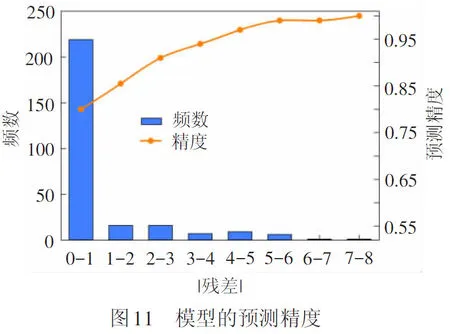
3.2 模型评估

表7所示为随机森林模型分别对训练集数据和测试集数据的计算精度，从表中可以看出，模型对所有样本的平均绝对误差在1 min以内，平均相对误差小于15%，由此可见模型对于的拟合及预测效果很好。

表7 随机森林模型的计算精度指标

为了更进一步评估随机森林模型的效果，本文还分别建立了代表传统统计建模方法的多元线性回归模型以及另一现代流行的机器学习算法——支持向量机模型(限于篇幅，未能在本文详细报道)，上述模型仍将PD、TD、RB和ZC作为自变量，RT作为因变量，训练集和测试集不变。将随机森林模型与多元线性回归模型、支持向量机模型进行允许误差下预测精度的比较见表8，结果表明：支持向量机模型预测能力与随机森林模型比较接近，它们都明显优于多元线性模型，但随机森林模型仍然是预测效果最佳的模型。

表8 不同允许误差下各模型预测精度对比 %

4 结论

本文获取了武广高速铁路列车运行实绩数据，提取出了了晚点列车运行数据(晚点时间大于4 min)，并对晚点列车晚点恢复时间以及晚点恢复时间的影响因素进行分析，确定了晚点列车在初始晚点站的晚点时间、列车晚点后经停各站的总停站缓冲时间和列车晚点后经各区间的总区间缓冲时间以及标识列车是否晚点通过株洲西—长沙南区间的0-1变量为自变量等4个晚点恢复时间的影响因素。根据各变量的分布情况以及变量之间的关系情况确定建立了列车晚点恢复时间预测的随机森林模型。模型有效性检验及预测结果表明：

(1) 随机森林模型能够很好地拟合高速列车初始晚点恢复的数据。

(2) 随机森林模型对高速列车初始晚点恢复时间具有很高预测精度，当允许误差在3 min以内时，模型的预测精度超过了90%。

(3) 随机森林模型与多元线性回归模型、支持向量机模型的对比结果显示，随机森林模型具有更优的预测精度。

本文基于中国高速铁路列车运行实绩研究了初始晚点的恢复模型，相比于传统的优化模型更加贴近于运输实际过程，在下一步研究中将考虑晚点列车在运行过程中受到二次干扰导致晚点增加的情况，建立更加完善的高速铁路列车晚点延误传播及恢复模型，丰富高速铁路行车指挥理论，为高速铁路调度指挥智能化提供理论指导及技术支撑。本文的研究只是基于我国高速列车大规模运行实绩数据进行列车运行晚点建模及行车指挥理论与方法研究的开始，还有大量的工作需要加速推进，如：(1)基于不同致因初始晚点的影响，探明不同致因初始晚点的影响程度，包括影响列车数、总影响时间等；(2)不同致因初始晚点与连带晚点的关系研究，构建基于大规模运行实绩数据的我国高速列车晚点传播及恢复模型，通过研究基于高速列车实绩的晚点传播及恢复的预测模型，建立高速铁路预测调度理论与方法。

TELET E, et al. A Model to Quantify the Resilience of Mass Railway Transportation Systems[J]. Reliability Engineering & System Safety, 2016, 153:1-14.

[6] KEIJI K, NAOHIKO H, SHIGERU M. Simulation Analysis of Train Operation to Recover Knock-on Delay under High-frequency Intervals[J]. Case Studies on Transport Policy, 2015, 3(1):92-98.

[7] YUAN J, HANSEN I A. Optimizing Capacity Utilization of Stations by Estimating Knock-on Train Delays[J]. Transportation Research Part B:Methodological, 2007, 41(2):202-217.

[8] MEESTER L E, MUNS S. Stochastic Delay Propagation in Railway Networks and Phase-type Distributions[J]. Transportation Research Part B:Methodological, 2007, 41(2):218-230.

[9] HANSEN I A, GOVERDE R M P,VAN DER MEER D J. Online Train Delay Recognition and Running Time Prediction[C]// Intelligent Transportation Systems (ITSC), 2010 13th International IEEE Conference on. New York: IEEE, 2010:1783-1788.

[10] WALLANDER J, M

KITALO M. Data Mining in Rail Transport Delay Chain Analysis[J]. International Journal of Shipping and Transport Logistics, 2012, 4(3):269-285.

[11] KHADILKAR H. Data-Enabled Stochastic Modeling for Evaluating Schedule Robustness of Railway Networks[J/OL]. Transport Science，2016:1161-1176[2016-12-05].https://pubsonline.informs.org/doi/10.1287/trsc.,2016.0703.

[12] MA M, WANG P, CHU C H, et al. Efficient Multipattern Event Processing Over High-Speed Train Data Streams[J]. IEEE Internet of Things Journal, 2017, 2(4):295-309.

[13] 刘健, 孟学雷, 王金霞. 突发事件下的列车运行图稳定性分析[J].铁路计算机应用,2015,24(9):1-5.

LIU Jian, MENG Xuelei, WANG Jinxia. Stability Analysis of Train Diagram in Emergency[J].Railway Computer Application,2015, 24(9):1-5.

[14] 庄河, 文超, 李忠灿, 等. 基于高速列车运行实绩的致因-初始晚点时长分布模型 [J]. 铁道学报, 2017, 39(9):25-31.

ZHUANG He, WEN Chao, LI Zhongcan, et al. Cause Based Primary Delay Distribution Models of High-speed Trains on Account of Operation Records [J]. Journal of the China Railway Society, 2017,39(9):25-31.

[15] XU P, CORMAN F, PENG Q. Analyzing Railway Disruptions and Their Impact on Delayed Traffic in Chinese High-speed Railway[J]. IFAC-Papers OnLine, 2016, 49(3):84-89.

[16] BREIMAN L. Random Forests[J]. Machine learning, 2001, 45(1):5-32.

[17] 文超, 彭其渊, 陈芋宏. 高速铁路列车运行冲突机理[J].交通运输工程学报, 2012, 12(2):119-126.

WEN Chao, PENG Qiyuan, CHEN Yuhong. Mechanism of Train Operation Conflict on High-speed Rail[J].Journal of Transportation Engineering, 2012, 12(2):119-126.

[18] BREIMAN L. Bagging Predictors[J]. Machine Learning, 1996, 24(2):123-140.