页岩储层多尺度渗流实验及数学模型研究

刘 华，王卫红，陈明君，刘启国，胡小虎

(1.页岩油气富集机理与有效开发国家重点实验室，北京 100083; 2.中国石化 石油勘探开发研究院，北京 100083; 3.西南石油大学，四川 成都 610500)

引 言

我国页岩气资源十分丰富[1-3]。据国土资源部《2012中国矿产资源报告》显示，我国页岩气地质资源潜力为134×1012m3，可采资源潜力为25×1012m3。页岩气藏不同于常规气藏[2-5]：基质赋存方式独特，自由气和吸附气共存；页岩孔隙结构复杂，存在纳米孔、微米孔、微裂隙、裂缝等，页岩储层致密，孔喉细小，基质渗透率通常小于0.001×10-3μm2，渗流不符合达西定律。美国页岩气勘探开发已经取得了巨大成功，国内中石化涪陵页岩气田已成功商业开发，目前累计产气量已超过100×108m3。

页岩气流动机理复杂，现有实验装置达不到真实模拟涪陵龙马溪组储层条件下的吸附/解吸、扩散、应力敏感等实验要求，国内外对页岩气储层多尺度复杂流动机理的认识尚不完全清楚。针对上述现状，通过改进实验装置，开展了涪陵龙马溪组储层条件下的吸附-解吸-渗流物理模拟实验，分析了页岩储层的特殊流动机理。基于实验及理论研究，建立了页岩储层多尺度综合渗流数学模型，为页岩气井渗流规律研究和动态分析奠定基础。

1 页岩储层多尺度渗流实验研究

1.1 页岩储层吸附/解吸实验

页岩气吸附/解吸特征是页岩气开发需要考虑的重要因素。目前国内主要开展常温、低压(小于20 MPa)吸附/解吸等温实验，高温高压吸附/解吸实验相关研究鲜有报道。针对涪陵龙马溪组页岩储层温度(82 ℃)、压力(38 MPa)的实际情况，优选带有高精度磁悬浮天平的重量法，开展储层条件下的吸附/解吸实验，分析吸附/解吸特征及影响因素，为涪陵页岩气井产能评价及数值模拟提供准确的基础参数。

1.1.1 不同温度下页岩样品的吸附/解吸 结合涪陵龙马溪组页岩储层的实际，选取粒度为60～80目的页岩颗粒样品，开展了42℃和82℃下的吸附/解吸实验，获取了不同温度下的页岩吸附/解吸实验曲线，实验结果见图1。从实验结果可以看出，实验样品对甲烷的吸附量随压力增大而逐渐升高，随温度增加而减小，解吸与吸附过程存在一定程度的滞后现象。对不同温度下页岩的吸附/解吸实验数据进行拟合， 基本符合兰格缪尔方程。 拟合结果同时表明，兰氏体积随温度增加而减小，兰氏压力随温度增加而增大。

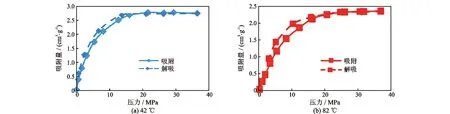
图1 涪陵龙马溪组实验样品在不同温度下的吸附/解吸曲线Fig.1 Adsorption/desorption curves of experimental samples from Fuling's Longmaxi formation at different temperatures

1.1.2 不同粒度页岩样品的吸附/解吸 选取涪陵龙马溪组储层粒度为60～80目和120～150目的颗粒样品，采用重量法，开展储层温度(82℃)下的吸附/解吸实验，获取了吸附/解吸实验曲线，实验结果见图2。对不同粒度页岩样品的吸附/解吸实验数据进行拟合，基本符合兰格缪尔方程。拟合结果表明，兰氏体积随样品粒度的减小而增大，兰氏压力随样品粒度的减小而减小。

1.2 页岩储层渗透率应力敏感实验

国内外对砂岩储层应力敏感研究比较深入，而关于高压页岩储层应力敏感性的报道较少[6-13]。目前实验室开展储层应力敏感实验时，通常采用变围压的实验方法，这种实验方法不能真实反映气藏开发过程中流体压力变化导致岩样基质膨胀对渗透率的影响。本文页岩渗透率应力敏感实验采用降内压的方法：实验中先逐步缓慢提高围压和孔隙压力值，直到流体压力达到实际地层压力值后保持流体压力值不变，再将围压增至实际上覆压力；然后保持围压和岩心两端驱替压差不变，逐步降低岩心两端的流动压力直至废弃压力；最后逐步同时升高岩心两端流动压力至原始地层压力，测试渗透率随有效应力的变化。实验过程中在出口端增加回压装置，可以更好地模拟气藏开发过程中流体压力从原始地层压力降到废弃压力条件的渗透率应力敏感情况。

图2 不同粒度涪陵龙马溪组实验样品的吸附/解吸曲线Fig.2 Adsorption/desorption curves of experimental samples with different particle size from Fuling's Longmaxi formation

根据实验要求，通过改进应力敏感实验装置，设计了一套能够模拟涪陵龙马溪组原始地层压力的应力敏感实验流程，整个实验装置测试压力高、密封性好、计量精度高，可以满足涪陵龙马溪组高压页岩储层应力敏感实验的需要。根据此实验流程，开展了模拟涪陵龙马溪组开发过程中天然裂缝和铺砂裂缝的渗透率应力敏感实验，评价储层的应力敏感程度，建立了储层渗透率随应力变化的数学模型。

1.2.1 天然裂缝页岩岩样应力敏感实验 根据实验流程，选取8块涪陵龙马溪组页岩储层天然裂缝岩心，开展模拟储层压力条件的应力敏感实验，获得了渗透率随有效应力的变化关系，实验结果见图3。

图3 天然裂缝页岩岩样无因次渗透率随有效应力变化曲线Fig.3 Change curves of dimensionless permeability with effective stress for the shale samples with natural fracture

从实验结果可以看出，渗透率随有效应力的增加而降低。无因次渗透率以有效应力40 MPa(有效应力增量约20 MPa)为分界点可以分为两段：有效应力低于40 MPa时渗透率急剧降低，有效应力高于40 MPa之后渗透率降低幅度减小。

对比8块岩心的渗透率变化曲线可以看出：渗透率越低应力敏感性越强，渗透率的整体损失也越大。对无因次渗透率与有效应力关系进行分段拟合，指数关系式拟合效果较好。

页岩样品的拟合方程式如下：

pi-pwf≤20 MPa，k/k0=1.037e-0.053(pi-pwf)；

(1)

pi-pwf>20 MPa，k/k1=1.013e-0.035(pi-pwf)。

(2)

涪陵龙马溪组天然裂缝页岩岩样的渗透率损害率69%～85%，其中6块岩样的渗透率损害率高于70%，总体上涪陵龙马溪组天然裂缝页岩岩样应力敏感性强。

对8块样品同时开展了增覆压和降覆压两种情况下的渗透率应力敏感实验。实验结果表明： 往复加压、 卸压时， 渗透率仅能恢复30%～45%。

1.2.2 铺砂裂缝页岩岩样应力敏感实验 选取7块涪陵龙马溪组页岩储层完整岩心，采用劈裂法进行人工造缝，根据现场压裂主要用30～50目和40～70目树酯覆膜砂的实际，采用2 kg/m2的铺砂浓度，开展了模拟储层压力条件下铺砂裂缝岩心的应力敏感实验，实验结果见图4。

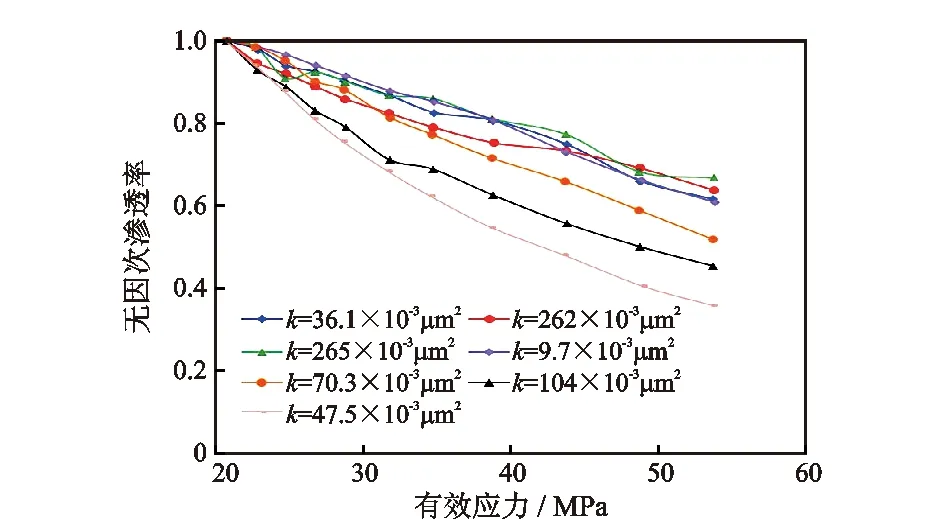
图4 人工铺砂裂缝页岩岩样无因次渗透率随有效应力变化曲线Fig.4 Change curves of dimensionless permeability with effective stress for the shale samples with artificial sanding fracture

从实验结果可以看出，人工铺砂裂缝页岩岩样渗透率随有效应力增加而降低，但总体降低幅度不大。当有效应力增加到53 MPa时，岩心的渗透率保持水平为60%～68%。

涪陵龙马溪组铺砂裂缝页岩岩样的渗透率损害率23%～48%，其中5块岩样的渗透率损害率小于40%，总体上涪陵龙马溪组铺砂裂缝页岩岩样的应力敏感程度为中等偏弱。增、降覆压应力敏感实验表明往复加压、卸压时渗透率可恢复60%～75%。

1.3 页岩储层气体扩散实验

采用涪陵龙马溪组页岩岩样，实验流体介质为99.99%甲烷，开展了涪陵龙马溪组页岩样品在不同温度、压力条件下的扩散系数测试实验，通过理论计算得到了页岩气层中的扩散系数。

1.3.1 不同压力下页岩样品的气体扩散实验 实验过程中保持温度82 ℃、围压59 MPa，孔隙压力由38 MPa逐渐降低至4 MPa。根据Fick第二定律计算有效扩散系数。实验结果表明甲烷在页岩中的有效扩散系数主要受孔隙压力的影响，龙马溪组储层条件下甲烷的有效扩散系数介于(6.7～19.7)×10-7cm2·s-1，实验结果见图5。

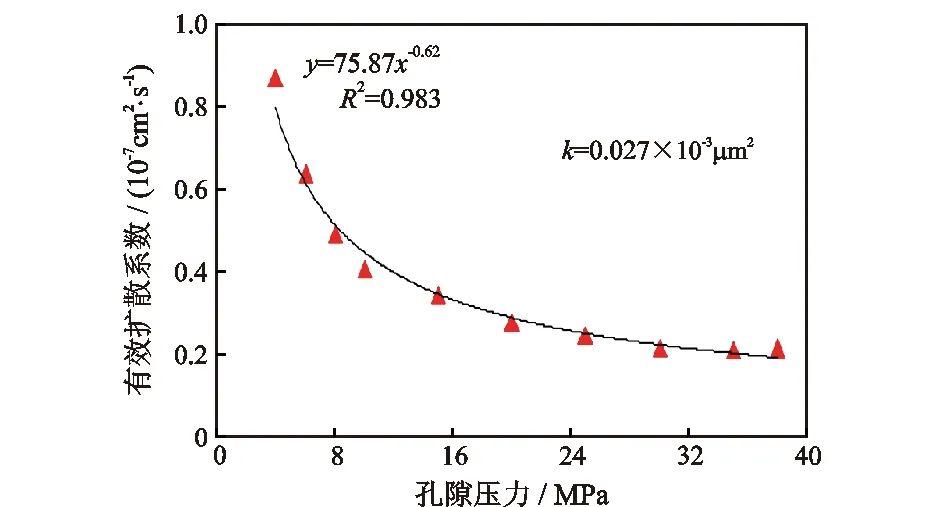
图5 页岩气体扩散系数随孔隙压力变化曲线Fig.5 Variation curve of shale gas diffusion coefficient with pore pressure

从图5可以看出：甲烷有效扩散系数随孔隙压力的增加而明显降低。该实验样品在38 MPa时的扩散系数仅为4 MPa时的1/4。分析认为有以下两方面的原因：一是孔隙压力增加，气体的分子自由程降低。根据经典扩散理论，扩散系数的大小与气相压力呈反比。另一方面，孔隙压力增加，甲烷在孔隙壁面上的吸附量显著增加，导致孔隙通道的有效直径减小，最终使气体扩散速率变慢。

从图5还可以看出：当孔隙压力小于10 MPa后，扩散系数对孔隙压力的变化更为敏感，主要原因是当压力小于10 MPa时，甲烷吸附量随压力的变化更为显著，甲烷气体的活性受压力的影响也更大。

1.3.2 不同温度下页岩样品的气体扩散实验 实验岩样为涪陵龙马溪组页岩，分别在42 ℃、62 ℃、82 ℃的恒温条件下开展扩散实验，孔隙压力由12 MPa逐渐降低至4 MPa，实验结果见图6。

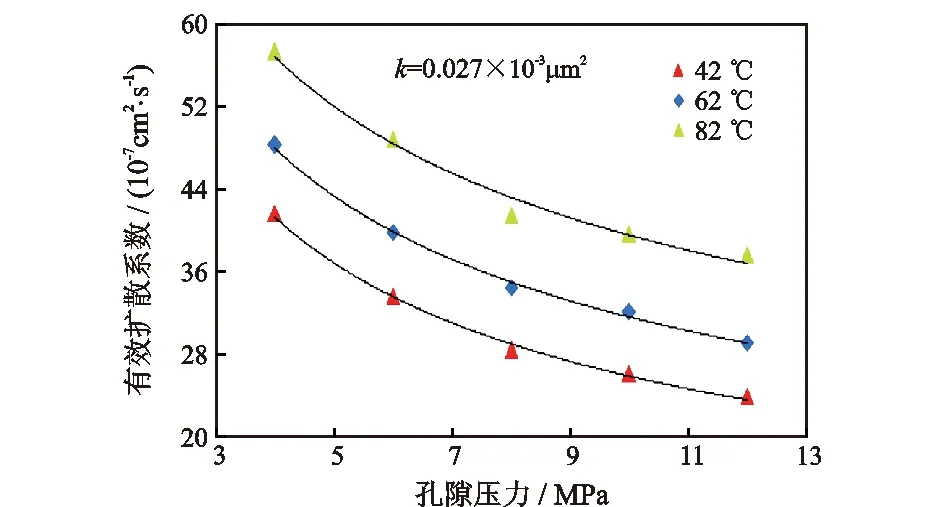
图6 不同温度下页岩气体扩散系数随空隙压力的变化Fig.6 Variation curves of shale gas diffusion coefficient with pore pressure at different temperatures

可以看出：同一温度下有效扩散系数随孔隙压力的降低而增大；有效扩散系数随温度的升高而明显增大。分析认为一是温度升高气体的活性增强，加快了扩散过程；二是温度升高有利于吸附气的解吸，扩散通道的有效直径变大。

2 页岩储层多尺度渗流数学模型

在上述页岩储层多尺度渗流实验及机理分析基础上，认为高温高压页岩储层的吸附/解吸符合Langmuir方程；页岩储层渗透率对应力敏感，渗透率与有效应力符合指数关系式；由于浓度差引起的扩散用Fick定律描述。结合国内外页岩气开发均采用大型压裂改造而形成大量人工裂缝的实际，认为页岩多尺度储层主要由基质系统和裂缝系统组成，页岩气在基质中的流动包括由压力差所引起的渗流、浓度差引起的扩散以及由于压力降低而引起的页岩气解吸，在裂缝中的流动主要是由压力差引起的渗流。建立了基质中同时存在渗流、扩散和吸附气解吸、裂缝中为达西渗流的页岩气藏综合渗流数学模型。

2.1 物理模型基本假设

(1)页岩储层由基质系统和裂缝系统组成，其中裂缝系统水平方向和垂直方向具有各向异性，即kfh≠kfv。

(2)忽略页岩储层的压缩性。

(3)裂缝系统中气体为游离气，其流动遵循Darcy定律。

(4)基质块形状为球形，基质中页岩气以吸附态和游离态两种状态存在。

(5)页岩气在基质中的流动是压力差和浓度差共同作用的结果，即同时存在Darcy渗流和气体扩散，扩散符合Fick定律。基质中页岩气在压力差的作用下以非稳态方式向裂缝系统窜流，且同时在浓度差作用下以非稳态方式向裂缝系统扩散。

(6)基于高温高压页岩储层吸附/解吸实验结果，基质中吸附气的解吸规律用Langmuir等温吸附定律描述。

(7)整个气藏在开采前处于平衡状态，吸附态和游离态气体处于动态平衡。

(8)气井以定产量生产，标况下气井产量为qsc。

(9)单相气体等温渗流，忽略重力影响。

2.2 渗流数学模型

模型中假设基质系统与裂缝系统之间的气体交换为压力差所引起的非稳态渗流和浓度差所引起的非稳态扩散，基质系统有其独立的流动微分方程和定解条件。

2.2.1 基质系统渗流微分方程 假设基质块为球形，基质中页岩气的流动为压力差和浓度差所引起的非稳态渗流和非稳态扩散，并考虑基质中吸附气解吸的影响，根据实验结果页岩气解吸选用Langmuir模型描述，可得到基质系统的渗流微分方程：

(3)

式中：ρsc为标况下气体密度，kg/m3；ρm为基质中气体密度，kg/m3；φm为基质系统孔隙度，小数；pm为基质系统压力，Pa。等号右端第二项代表当压力降低时基质中吸附气解吸的影响。

式(3)中气体流动速度vm为压力差和浓度差共同作用下的气体总速度，可写成：

(4)

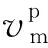
将气体状态方程代入连续性方程式，可得：

(5)

式中：cgm为基质系统中气体压缩系数，Pa-1。

引入拟时间和拟压力可得到综合考虑解吸、非稳态扩散和非稳态渗流多重机制作用的基质系统微分方程：

(6)

对上述基质系统渗流微分方程组无因次化，可得数学模型：

(7)

2.2.2 裂缝系统渗流微分方程 假设页岩气在裂缝中的流动为Darcy渗流，基质中页岩气向裂缝同时进行非稳态窜流和非稳态扩散，再结合质量守恒定律，可得到裂缝系统的渗流微分方程：

(8)

利用拟压力定义，取μ和cgf为气藏初始状态下的值对式(8)进行线性化处理，可得：

(9)

式(9)左端第4项代表基质中页岩气向裂缝系统非稳态窜流和非稳态扩散的影响。结合渗流实验结果，页岩储层具有强应力敏感，渗透率与有效应力符合指数关系式。拟压力的无因次定义如下：

对式(9)进行无因次化，可得：

(10)

2.2.3 系统综合渗流微分方程 对裂缝系统无因次渗流微分方程进行基于tD的Laplace变换，并利用基质系统压力和裂缝系统压力的关系，对裂缝系统渗流微分方程进行化简，可以得到页岩气藏最终的综合渗流微分方程：

(11)

式(11)中

(12)

式(11)即为反映页岩气藏解吸、应力敏感、非稳态扩散的三维无限大双重介质综合渗流微分方程。

3 结论与认识

(1)吸附/解吸实验结果表明，页岩吸附量随温度升高而减少；随温度升高，兰氏体积降低，兰氏压力增加；储层条件下的解吸曲线相比吸附曲线略有滞后；Langmuir模型可描述涪陵龙马溪组储层条件下的等温吸附/解吸过程。

(2)渗透率应力敏感实验结果表明，天然裂缝页岩岩心渗透率随有效应力的增加而降低，并以有效应力40 MPa为分界点，有效应力低于40 MPa时渗透率急剧降低，高于40 MPa之后渗透率降低幅度减小。无因次渗透率与有效应力符合指数关系式；涪陵龙马溪组天然裂缝页岩岩样具有强应力敏感性，铺砂裂缝页岩岩样的应力敏感程度为中等偏弱。

(3)扩散实验结果表明，甲烷扩散系数随温度升高及孔隙压力降低而增大，扩散符合Fick定律。

(4)基于实验及理论分析所建立的考虑解吸、应力敏感、非稳态扩散的页岩多尺度储层综合渗流数学模型，为页岩气井渗流规律研究和动态分析奠定了基础。