考虑扩散比影响的突扩水跃共轭水深计算研究
渠亚伟, 宁利中, 宁碧波, 王新宏, 刘 爽, 田伟利
(1.西安理工大学 西北旱区生态水利工程国家重点实验室培育基地, 陕西 西安 710048;2.嘉兴学院 建筑工程学院, 浙江 嘉兴 314001; 3.上海大学 建筑系, 上海 200444)
1 研究背景
水利枢纽的建设一般会增大上下游的水位落差,从而使得下泄水流具有较大的单宽能量,若不采取有效的消能及防护措施,则会严重冲刷下游河床,对整个枢纽建筑物的稳定带来不利影响[1]。水流在通过水闸、溢流坝等水工建筑物时,原水流的过流边界条件已发生了改变,水流的流速增大,而高速水流具有很强的复杂性[2],会出现各种复杂的水力现象,高速水流的消能防冲是水利工程中的一项重要课题[3-4]。
消能工的作用[5-6]就是减少水流携带的能量,改变水流流态和形态,通过促使水流发生横向或纵向扩散紊乱,以热能的形式消耗水流的能量,从而保护下游河床,以防发生严重的冲刷。依据具体的工程实际情况选择合适的消能方式以及设计、布置合理的消能工成为关乎水利枢纽工程运行安全的重要课题[6-10]。
底流消能(水跃消能)具有消能率较高、对河床的冲刷较小以及对地质条件要求不高等优点[11],是水利工程中泄洪消能的主要形式之一。如苏联的萨扬舒申斯克水电站[12]、印度的特里水电站大坝[13]、葛洲坝水利枢纽的二江泄水闸[14]、辽宁清原下水库[15]均采用了底流消能形式,并且消能效果良好。
水跃可以从不同的角度进行分类[1]。从过流断面上来讲,其中最简单的情况是发生在沿程为平底等宽矩形断面河道中的水跃。Chow[16]求解出了最简单情况下的共轭水深计算式;Hager等[17]研究了在光滑壁面条件下,剪应力与最简单水跃形式之间的关系;Ead等[18]认为河床形态会对水跃产生较大的影响。而确定消力池尺寸的影响因素较多,从而引起了学者对平底空间水跃的关注。
突扩水跃经常在闸下出流的情况下出现,多孔闸中部分闸门工作时,水流经过闸室后流入突然扩散的渠道,过流条件发生改变,使水流在横向上有扩散趋势,从而形成一种复杂的三维流态,该水流现象也发生在采用水闸泵站合建布置的枢纽系统中。Bremen等[19]以水跃发生的位置为参考标准,把平底突扩渠道中的水跃分为R型水跃、S型水跃、T型水跃和经典水跃4类。R型水跃是指水跃完全发生在突扩断面下游渠道;S型水跃是指恰好发生在突扩断面的水跃,示意图如图1所示;T型水跃是指水跃的一部分在突扩断面的上游、一部分在突扩断面的下游;经典水跃是指水跃完全发生在突扩断面上游渠道。本文主要讨论S型水跃的水力特性。
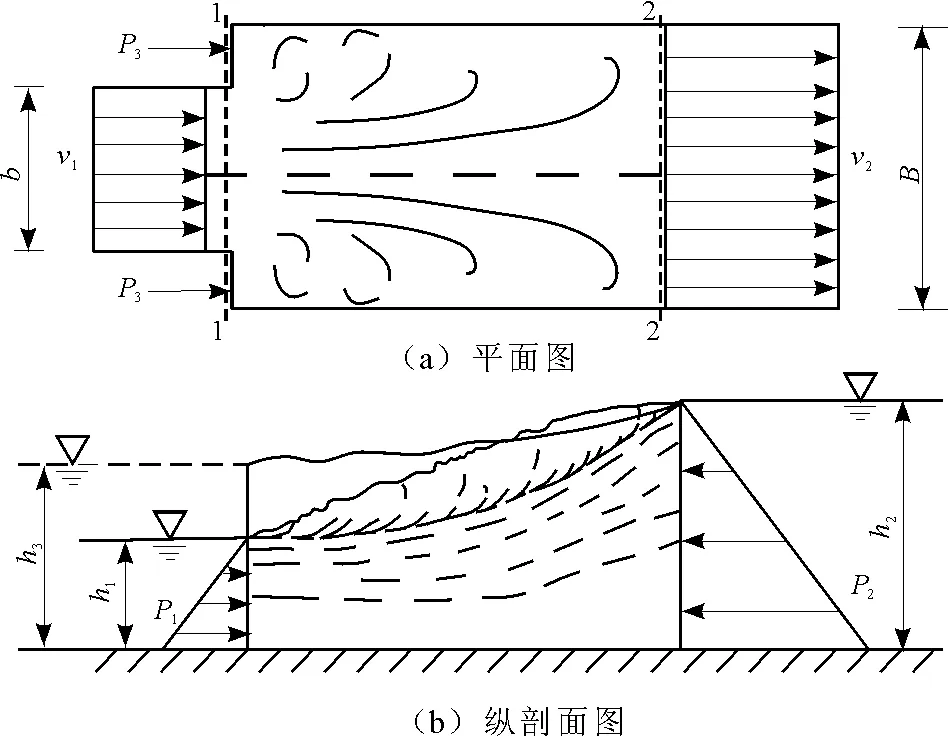
图1 S型水跃示意图
2 一个新的突扩水跃共轭水深方程
2.1 突扩水跃方程
引入3条假定:(1)研究对象视为渐变流,服从静水压强分布;(2)动量系数为1;(3)忽略壁面摩阻力,对1-1断面和2-2断面之间的研究对象列动量方程和连续方程:
=α2ρQv2-α1ρQv1
(1)
Q=v1h1b=v2h2B
(2)
式中:h1、h2分别为跃前、跃后断面水深,m;h3为回流区平均水深,m;b、B分别为上游、下游河道宽,m;g为重力加速度,m/s2;ρ为流体密度,kg/m3;v1、v2分别为跃前、跃后断面平均流速,m/s;Q为过流流量,m3/s;α1、α2为动量修正系数,均取为1。
前人对回流区水深作出了一些假设,并得到了相应的理论方程。Hasan等[20]引入h3=h1的假设,得出:
(3)
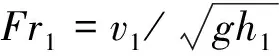
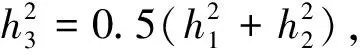
(4)
卢士强[22]假定h3=0.5(h1+h2),得出:
(5)
从以上可以看出,由于突扩断面的水流流态十分复杂,既有沿主流方向的扩散,也有两边的回流扩散,而各研究者根据对突扩端壁断面反力作出的不同假设,得到的计算方程也不相同。
本文由突扩水跃的流态特征,提出了一种新的假设,即h3=a(h1+h2),a为待定系数。联立方程(1)、(2),并将假设关系代入,得到新的突扩水跃共轭水深方程为:
(6)
在方程(6)中,看似有突扩比β、共轭水深比η以及待定系数a共3个未知量,但是实际应用计算时,突扩比β一般为已知条件,所以方程(6)为共轭水深比η和待定系数a的二元方程。
如果方程式(6)中β=1,则简化为等宽二元水跃,与Belanger方程相同:
(7)
2.2系数a的确定
由于突然扩散段两侧存在回流区,回流漩涡和主流之间的剪切作用促使主流扩散,再加上侧壁阻碍着回流区的水流扩散,会对主流存在着一定的挤压作用,近主流侧水深接近跃前水深,近边壁测水深较高些,但又不会超过跃后水深,导致回流区的水流面为一倾斜面,如图2所示。
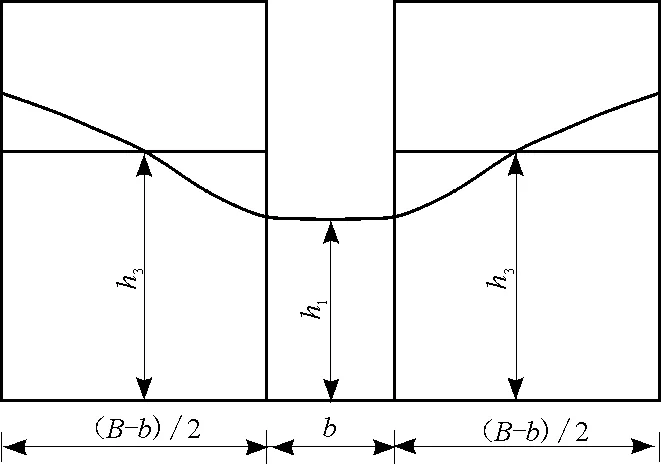
图2 突扩断面回流区水深示意图
由图2可以看出,近主流侧水深比h1略高,远主流侧水深较高,其水深受h2影响。由Rajaratnam等[23]和文献[22]的回流区平均水深实验资料可得,弗氏数对回流区水深的影响较小,可以忽略不计。由于水流之间的混掺与挤压作用,水跃段内的水深必定是水流在紊流状态下形成的一个毫无规则的水面。水面不规则的程度与水流扩散程度、旋滚区与主流之间的质量交换情况等因素有关,而渠道扩散的程度同时对这两个因素产生了影响。所以,回流区的水深应该与渠道的扩散比有关,应当把扩散比考虑在内。在这里假设一个水深来描述水跃段始端的水流,这个水深反映出回流区始端壁面的压力分布。表1中是利用实验所得数据,按照新假设关系计算得到不同扩散比下a值的平均取值情况。

表1 不同突扩比β下的a值
a值与扩散比β的关系曲线见图3。由图3可见,a值与扩散比β的关系近似为二次函数,拟合方程为:
a=-0.0244β2+0.1663β+0.2559
(8)
式中:1.2≤β≤5.0。
讨论a与β的关系,随着扩散比β的增大,a值也增大;而扩散比β继续增大,a值反而逐渐衰减。在扩散比较小时,随着扩散比的增大,回流区越大,回流漩涡也越大,边壁对回流漩涡的阻碍作用逐渐加强,回流漩涡与主流之间的剪切作用也越大,回流漩涡与主流之间的相互挤压效果也明显,导致回流区的水深也逐渐增加;随着扩散比的进一步扩大,主流逐渐脱离边壁,边壁对回流漩涡的阻碍作用逐渐减弱,回流漩涡也越小,回流漩涡与主流之间的剪切作用也减小,回流漩涡阻碍主流的扩散作用也逐渐减弱,回流区逐渐减小,水深降低。
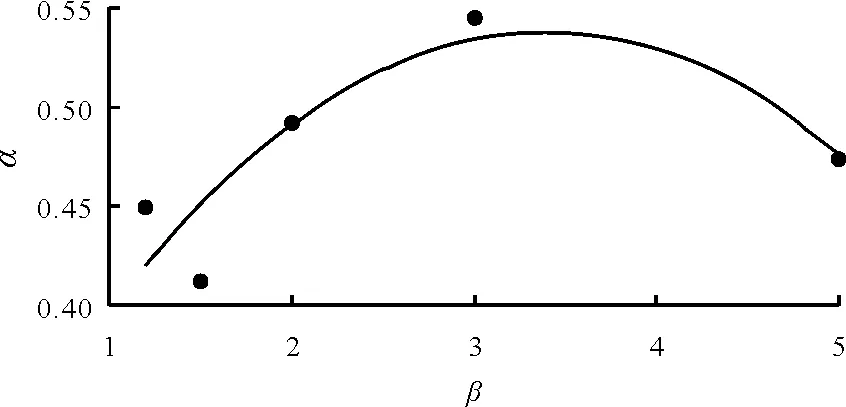
图3 a与β的关系
3 计算结果的验证
3.1 对文献[22]中实验数据可靠性的验证
当扩散比为1时,方程(3)~(6)均与Belanger方程相同。在此选用方程(6)来验证文献[22]中实验数据的可靠程度,计算结果见表2。
在此扩散比下,把按照理论计算方程得到的共轭水深比和实测值绘于图4。图4和表2的结果表明,文献[22]中的实验数据是可靠的。
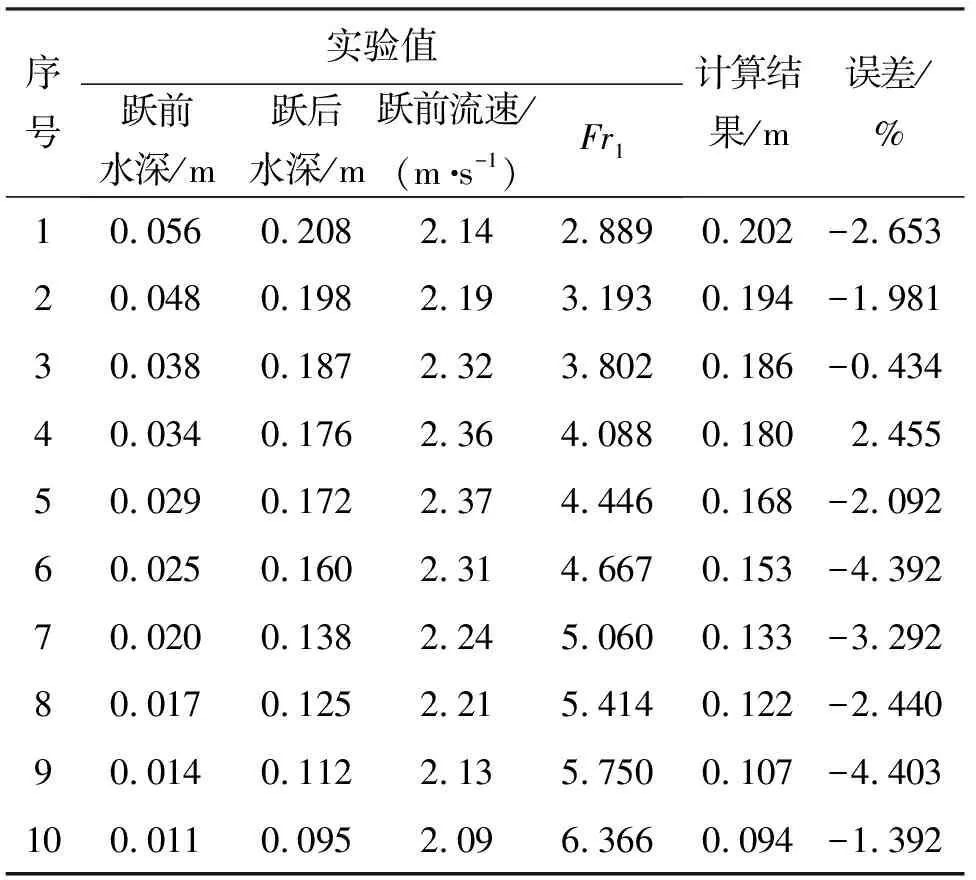
表2 计算结果与实验的比较(β=1)
3.2 不同共轭水深方程计算结果的比较
文献[22]和文献[23]的实验条件如表3所示,数据共有90组,本文利用这90组数据分别对方程(3)、方程(4)、方程(5)和新方程进行了跃后水深及其于试验值误差的计算。
由计算结果得到,在90组数据中,首先,方程(3)只有5组计算结果大于实测值,表明方程(3)总体偏小;而且随着突扩比的增大,对应跃后水深计算结果的平均误差明显增大,总体来说,方程(3)平均误差为11.806%,最大误差为40.841%;其次,方程(4),在90组数据中,共有59组计算结果小于实测值,方程(4)偏于安全,平均误差为6.761%,最大误差为29.206%;然后再看方程(5),在90组数据中,有49组数据的计算值大于实测值,平均误差为6.331%,最大误差为32.420%;最后本文方程,在90组数据中,有36组数据的计算结果大于实测值,平均误差为5.956%,最大误差为30.135%,其值都比其它方程低。由此可见,假定h3=h1时,得到的计算精度最差,整体上跃后水深偏小,表明计算时边墙反力偏小,所以在工程应用时并不安全;假定h3=a(h1+h2),并且考虑到a在不同的扩散比下的取值时,计算的水跃跃后水深精度最高,与实际情况更为接近。
将不同扩散比下,把按照理论计算方程计算得到的共轭水深比与实测值绘于图5(a)~5(e)。
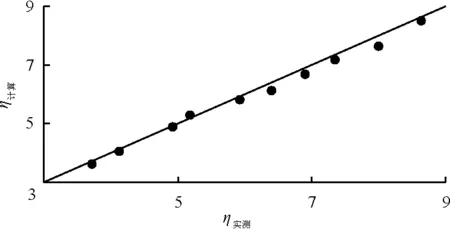
图4 β=1.0时共轭水深比计算值与实验的比较
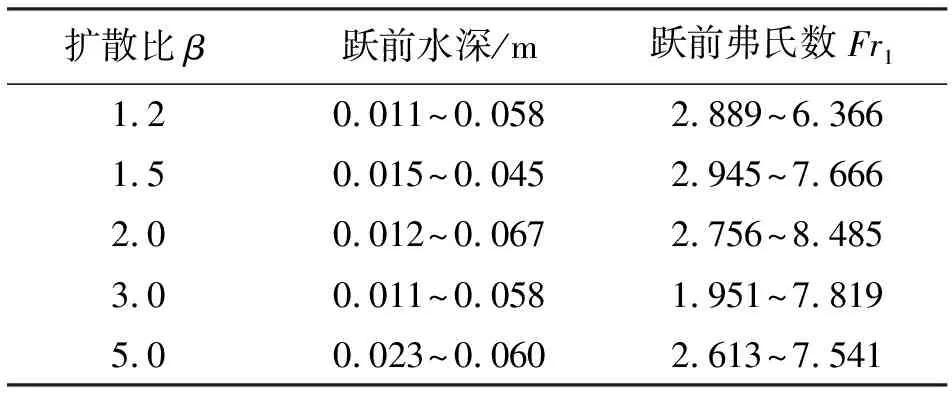
扩散比β跃前水深/m跃前弗氏数Fr11.20.011~0.0582.889~6.3661.50.015~0.0452.945~7.6662.00.012~0.0672.756~8.4853.00.011~0.0581.951~7.8195.00.023~0.0602.613~7.541
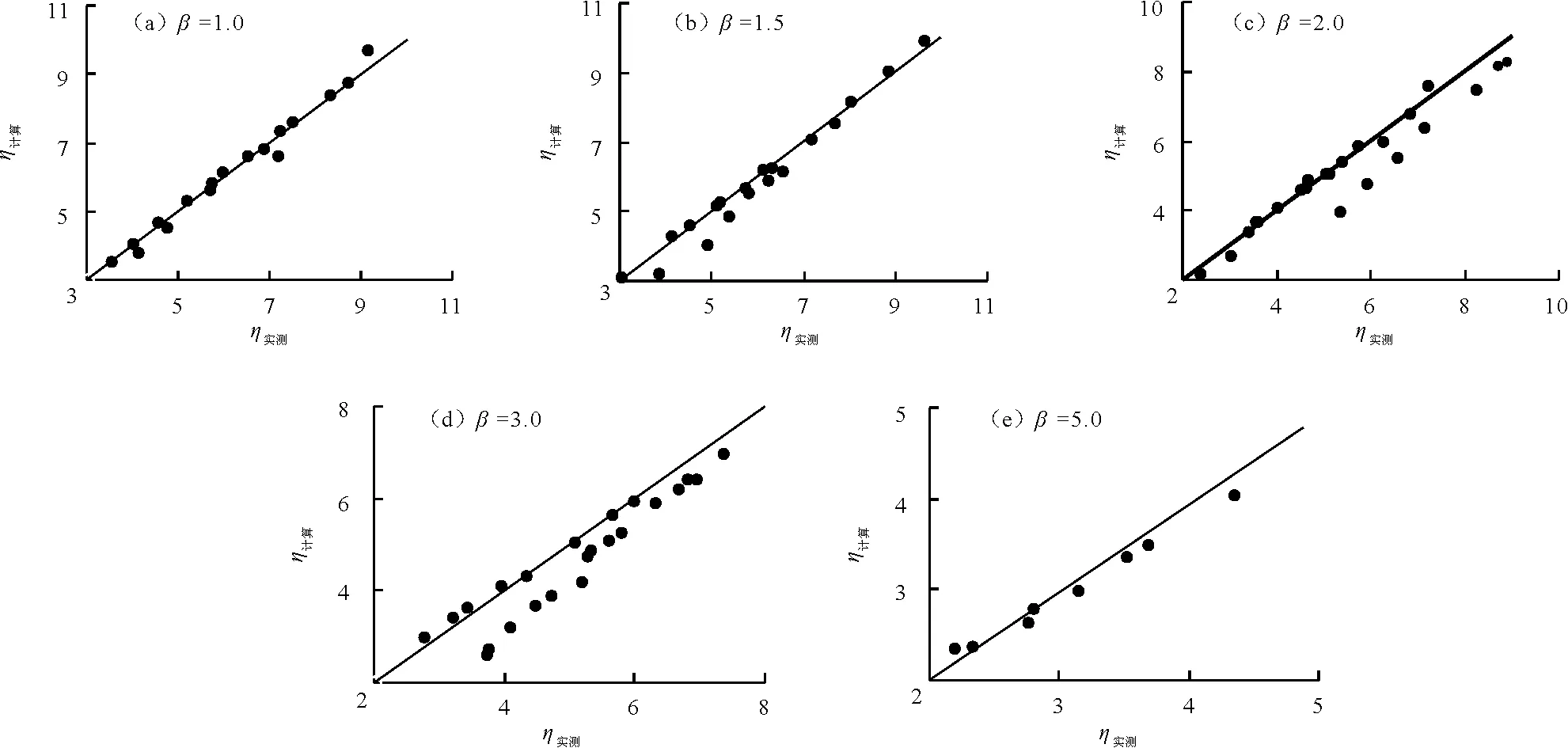
图5 共轭水深比计算结果与实验结果的比较
观察图5(a)~5(e),计算共轭水深比和实测共轭水深比整体上吻合较好。不同突扩比情况下,方程(6)与实验的误差见表4。可以看出,在5组扩散比中,扩散比β=3.0时,平均误差、最大误差最大;扩散比β=1.2时,平均误差,最大误差均较小。分析原因可能是随着扩散比的增大,水流的表面旋滚区与主流之间混掺作用越剧烈,水流受到边壁的作用减弱,最终致使水流流态更加紊乱,对测量试验各参数的影响越大,所以试验误差随着扩散比的增大而增加。
综上所述,本文提出的关于回流区平均水深与跃前、跃后断面水深的关系更符合实际,并由此假设得到理论方程使整体的计算结果的精度得到提高,并且降低了数据的离散程度,说明本文方法是可靠的。
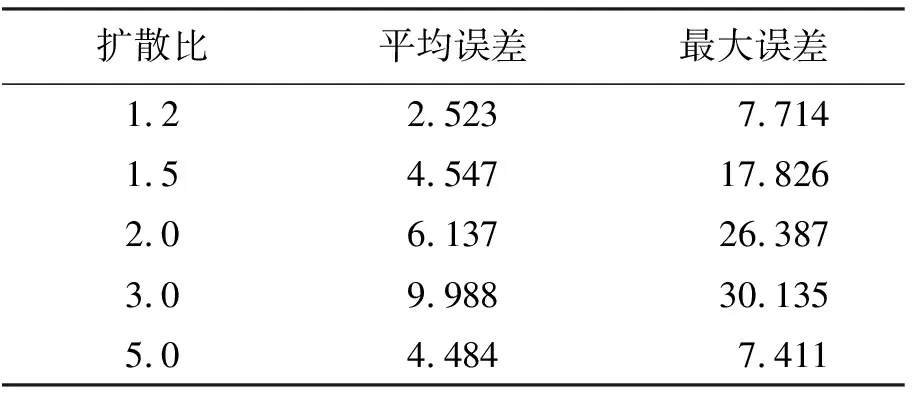
表4 不同扩散比下本文方程的误差 %
4 结 论
(1)本文总结了前人对突扩水跃回流区水深所做出相关假设的基础上,做出了考虑扩散比影响的回流水深新假设,并得到新的共轭水深理论方程。
(2)依据试验数据,给出了回流水深中参数α随着扩散比β变化的关系式,确定了回流水深的计算方法。
(3)利用其他学者的试验数据,对本文提出的理论方程进行了计算,并将计算结果与其他方程作出了比较,证明本文提出的理论方程平均误差最小,精度更高。
(4)本文提出的理论方程对实际工程中确定消力池的尺寸提供了更加精准的计算方法。目前关于突扩水跃共轭水深的物理试验模型和理论分析模型较多,而数值模拟并不多。数值模拟主要依靠计算机,具有计算速度快,成本低廉,计算模型更改方便等优点,今后应该多结合数值模拟的方法进行研究。

