基于模糊近似空间组合度量的特征选择算法

费贤举，刘金硕，田国忠

(1.常州工学院 计算机信息工程学院，江苏 常州 213032；2.武汉大学 计算机学院，湖北 武汉 430072)

0 引 言

在特征选择[1-11]算法中，如何对属性的重要度进行更精确的评估一直是特征选择的研究重点，目前学者们提出了多种的度量方法。例如翟俊海等[3]利用属性的相关性作为度量方法，提出一种特征选择算法，陈媛等[4]利用一致性度量进行特征选择，Wang等[5,6]利用距离度量进行特征选择，Jiang等[7]和Zhao等[8]利用粗糙集理论的依赖度度量用于特征选择算法的构造，近年来，信息熵度量[9-11]用于特征选择的方法被大量提出。目前信息熵已作为一种常用的属性度量方法。

粒计算理论由Zadeh[12]提出，目前已在智能信息处理领域发挥着重要的作用[13]，其中模糊近似空间[14]是粒计算理论一种重要的形式，它以模糊集理论[15]为基础，将信息系统中的对象按照一定的相似关系进行粒化，并生成相应的信息粒，通过信息粒的全体可以组成信息系统的粒空间，粒空间是粒计算中一个重要的概念[16-18]，它是对信息系统各个方面度量的基础。因此可以考虑运用粒计算模型来对属性进行评估，从而达到更好度量效果。

在模糊近似空间中，本文首先在信息系统中构造模糊粒空间，然后在此基础上引入了模糊粒度度量，由于模糊粒度是对信息系统分类能力的体现[17]，因而可以作为属性重要度的一种评估方式。信息熵是特征选择中一种重要的方法[9-11]，本文将条件熵[19]在模糊近似空间中进行推广，提出了模糊条件熵的概念。模糊粒度和模糊条件熵代表了不同的评估视角，为了对属性进行多视角的度量，本文将模糊条件熵与模糊粒度结合起来，提出一种组合度量方法来对属性重要度进行评估，同时给出了相应的特征选择算法，UCI实验结果表明，本文所构造出的算法比目前已有的特征选择算法更具一定优越性。

1 模糊集与模糊二元粒空间

在粒计算模型[12]中，数据集又称为信息系统，可表示为IS=(U,AT,V,f)，其中U被称为论域，AT为属性集(特征集)，V为全体属性集的值域，V=∪Va，其中Va为属性a∈AT的值域，f为属性到属性值域上的映射，对象x在属性a的值可表示为a(x)。当信息系统IS=(U,C∪D,V,f)时，此信息系统又被称为决策信息系统(DIS)，其中C,D分别被称为信息系统的条件属性和决策属性。若条件属性均为数值型数据，此信息系统称为邻域信息系统。

定义1[18]对于邻域信息系统NIS=(U,AT,V,f)，由B⊆AT在U上诱导的模糊二元关系RB满足关系:①∀x∈U，RB(x,x)=1，②∀x,y∈U，RB(x,y)=RB(y,x),设|U|=n，那么模糊二元关系RB可由矩阵表示为

(1)

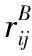
定义2[18]对于邻域信息系统NIS=(U,AT,V,f)，B⊆AT在U上诱导的模糊二元关系为RB，RB在论域上的模糊粒空间定义为

K(RB)=(SRB(x1),SRB(x2),…,SRB(xn)),xi∈U(2)

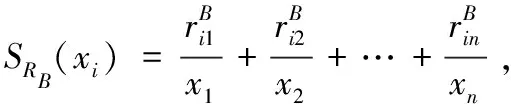
2 模糊近似空间组合度量

2.1 模糊粒度

在信息系统的不确定性度量中，基于模糊近似空间的粒空间一直是常用的度量体系，目前研究人员们提出了大量的度量方法。如Huang等学者[17]定义了模糊粒度的概念。

定义3[17]设邻域信息系统NIS=(U,AT,V,f)，B⊆AT在U上对应的模糊二元关系为RB，导出的模糊粒空间为K(RB)=(SRB(x1),SRB(x2),…,SRB(xn))，那么RB在U上的模糊粒度GK(B)定义为

(3)

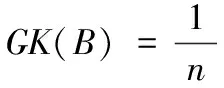
性质1 对于邻域信息系统NIS=(U,AT,V,f),B1⊆B2⊆AT在U上对应的模糊二元关系分别为RB1,RB2，导出的对应模糊粒空间为K(RB1)=(SRB1(x1),SRB1(x2),…,SRB1(xn)),K(RB2)=(SRB2(x1),SRB2(x2),…,SRB2(xn))，那么模糊粒度满足GK(B2)≤GK(B1)。

证明：由于B1⊆B2，根据定义1有RB2⊆RB1，因此有∀x∈U,SRB2(x)⊆SRB1(x)，即|SRB2(x)|≤|SRB1(x)|，根据定义3有GK(B2)≤GK(B1)。证毕。

通过性质1可以看出，随着属性集B的逐渐增加，其模糊粒度是单调不增的，即当对象的模糊信息粒越精细时，模糊粒度就越小，当对象的模糊信息粒越粗糙时，模糊粒度就越大，因此模糊粒度体现了模糊二元关系对论域知识粒度划分能力的度量。

2.2 模糊条件熵

Liang等[20]学者提出了信息系统中的信息熵模型，为粒计算中的熵理论研究奠定了基础，文献[18,19]在此基础上定义了基于信息系统的条件熵模型。条件熵是一种构造特征选择常用的方法。随后很多学者将条件熵理论推广到各个模型中[21]。本文在此基础上，将条件熵引入到模糊近似空间中，提出模糊条件熵模型。

定义4 设邻域信息系统NIS=(U,AT,V,f),B⊆AT在U上诱导的模糊二元关系为RB，其模糊粒空间为K(RB)=(SRB(x1),SRB(x2),…,SRB(xn))，定义RB下的模糊信息熵[18]FE(B)为

(4)

对于∀xi∈U，当SRB(xi)={xi}时，有FE(B)=1-1/n，对于∀xi∈U,SRB(xi)=U时，有FE(B)=0，因此可以推出模糊信息熵满足0≤FE(B)≤1-1/n。

定义5 设邻域信息系统NIS=(U,AT,V,f),B1,B2⊆AT在U上的诱导的模糊二元关系分别为RB1,RB2，其对应的模糊粒空间为K(RB1)=(SRB1(x1),SRB1(x2),…,SRB1(xn)),K(RB2)=(SRB2(x1),SRB2(x2),…,SRB2(xn))，定义RB2关于RB1的模糊条件熵FCE(B2|B1)为

(5)

类似于定义4，模糊条件熵满足0≤FCE(B2|B1)≤1-1/n。

对于邻域决策信息系统NDIS=(U,C∪D,V,f),B⊆C在U上的诱导的模糊二元关系分别为RB，对应的模糊粒空间为K(RB)，决策属性D诱导的等价关系为RD，那么RB关于RD的模糊条件熵FCE(D|B)为

(6)

这里[x]D表示对象xi在D下的等价类。

性质2 设邻域决策信息系统NDIS=(U,C∪D,V,f),B1⊆B2⊆C在U上的诱导的模糊二元关系分别为RB1,RB2，其对应的模糊粒空间为K(RB1),K(RB2)，那么模糊条件熵满足

FCE(D|B2)≤FCE(D|B1)

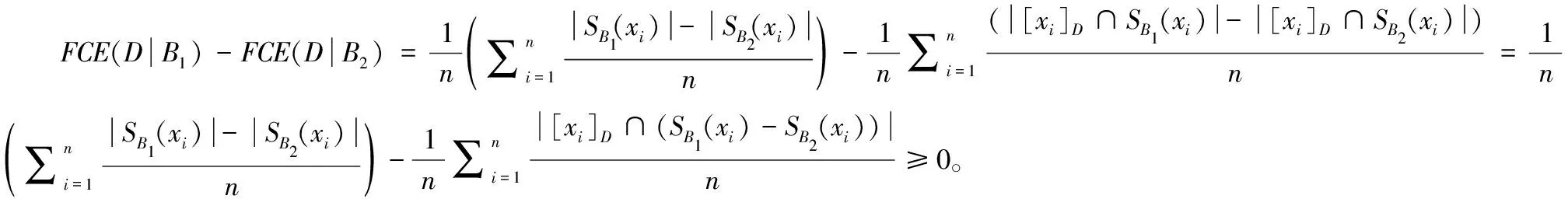
性质1和性质2表明，随着属性集B的逐渐增大，其模糊条件熵FCE(D|B)和模糊粒度的值都是单调不增的，因此它们都可以作为信息系统中属性集的不确定性度量，由于模糊粒度和模糊条件熵代表了不同视角下的度量方法，因此可以将它们结合起来，提出一种组合的信息系统不确定性度量。

定义6 设邻域决策信息系统NDIS=(U,C∪D,V,f),B⊆C在U上的诱导的模糊二元关系为RB，其对应的模糊粒空间为K(RB)，那么在模糊近似空间中D关于B组合度量定义为

M(B,D)=GK(B)·FCE(D|B)

(7)

随着属性集B的逐渐增大，根据性质1和性质2结论，组合度量M(B,D)的值是单调不增的。由于1/n≤GK(B)≤1, 0≤FCE(D|B)≤1-1/n，所以组合度量满足0≤M(B,D)≤1-1/n。组合度量的单调性为接下来的特征选择算法的构造提供了理论基础。

定义7[8]设邻域决策信息系统NDIS=(U,C∪D,V,f),B⊆C为该决策信息系统的一个相对约简当且仅当：

(1)M(C,D)=M(B,D)；

(2)∀a∈B,M(B-{a},D)>M(B,D)。

定义8[9]设邻域决策信息系统NDIS=(U,C∪D,V,f),B⊆C, ∀a∈B，则a关于B在决策属性D下的重要度定义为

(8)

对于∀a∈C-B，则a关于B在决策属性D下的重要度定义为

(9)

3 特征选择算法

基于定义8给出的信息系统重要度的定义，这里构造出相应的特征算法—基于模糊近似空间组合度量的数值特征选择算法FSFASCM(feature selection based on fuzzy approximation space combination metric)。首先算法1给出的是组合度量的计算方法。

算法1：组合度量。

输入：NDIS=(U,C∪D,V,f)，属性子集B⊆C, |U|=n。

输出：M(B,D)。

(1)初始化GK(B)=0,FCE(D|B)=0。

(2)对于∀xi∈U，计算SRB(xi), [xi]D。然后根据定义3和定义5对模糊粒度GK(B)和模糊条件熵FCE(D|B)进行累加，即：GK(B)←GK(B)+|SRB(xi)|,FCE(D|B)←FCE(D|B)+(|SRB(xi)|-|SRB(xi)-[xi]D|)。

(3)进行计算

(4)返回组合度量值

M(B,D)=GK(B)·FCE(D|B)

设|C|=c, |U|=n，算法1的计算时间主要集中在步骤(2)，由于每个对象计算模糊信息粒的时间复杂度为O(c·n)，因此整个算法1的时间复杂度为O(c·n2)。根据算法1，接下来给出本文提出的特征选择的主算法，具体如算法2所示。

算法2：模糊近似空间组合度量特征选择算法(FSFASCM)。

输入：NDIS=(U,C∪D,V,f)。

输出：约简集S。

(1)初始化：S=∅。

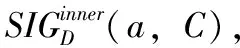
(3)根据算法1，若M(S,D)=M(C,D)，那么进入步骤(5)，否则进入步骤(4)。

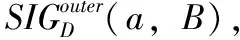
(5)令集合φ←∅，对于∀a∈S，如果M(S-{a},D)=M(C,D)，那么φ←φ∪{a}。

(6)如果φ为空，那么进入步骤(7)，否则，任意选择φ中的一个属性a，进行S=S-{a}，并进入步骤(5)。

(7)返回约简集S。

设|C|=c, |U|=n，算法2的时间复杂度主要集中在步骤(2)，因此整个算法2的时间复杂度为O(c2·n2)。

4 实验分析

为了验证本文所提特征选择算法的优越性，本实验从UCI标准数据集库下载了6个数据集，见表1，然后将所提的算法与目前已有的相关算法对这些数据集进行实验分析，优越性的比较通过各个算法的特征子集、分类精度和运行时间来体现。参与比较的算法分别为：①模糊邻域粗糙集特征选择算法FSFNRS(feature selection based on fuzzy neighborhood rough sets)[22]；②模糊粗糙集拟合模型的特征选择算法FSFRSFM(feature selection based on fuzzy rough set fitting model)[6]；③基于邻域熵的特征选择算法FSNE(feature selection based on neighborhood entropy)[23]。

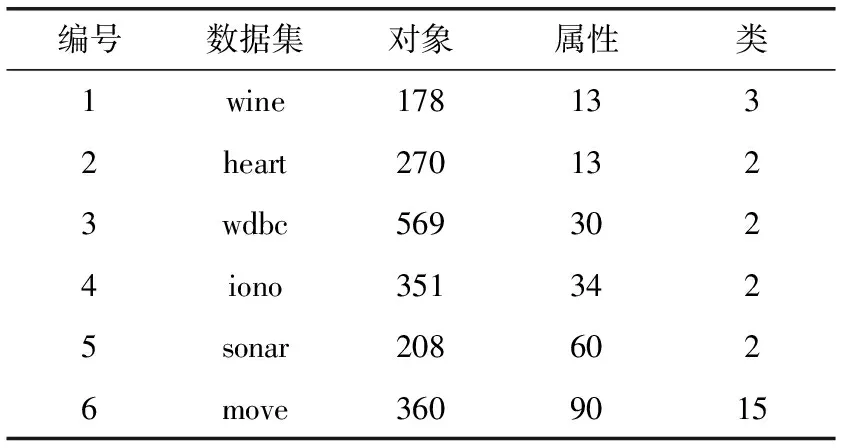
表1 数据集详细信息

为了消除属性量纲的影响，表1中的数据集属性值均被归一化到[0,1]区间，本实验运行的硬件环境为Intel(R) 酷睿i5 680，3.6 GHz CPU和4.0 GB RAM，Windows7操作系统，编程工具选为JDK1.8。实验中分类精度的计算采用支持向量机(SVM)和决策树(C4.5)两种分类器。

表2所示的是4种算法在各个数据集上特征选择结果，其中包括具体的属性子集结果和属性子集大小。观察表2可以看出，4种特征选择算法得到的属性子集并不相同，例如在数据集Wine的结果中，4种算法得到的属性子集都包含序号为1，2，7，11，13的属性，说明这些属性对Wine数据集的分类发挥关键的作用，但是除了这些属性，其它的每种算法的结果并不相同，说明其它的属性对分类的作用比较低，不同的算法对这些属性的鉴别能力不同，从而引起了属性子集结果的差异。同时可以看出，在大部分数据集中，本文所提的FSFASCM算法选择出的属性子集大小更小一些，这主要是由于在算法2中，我们对按照属性重要度选择出的特征子集利用组合度量进行了进一步的筛选，从而能够选择出更为关键的属性。

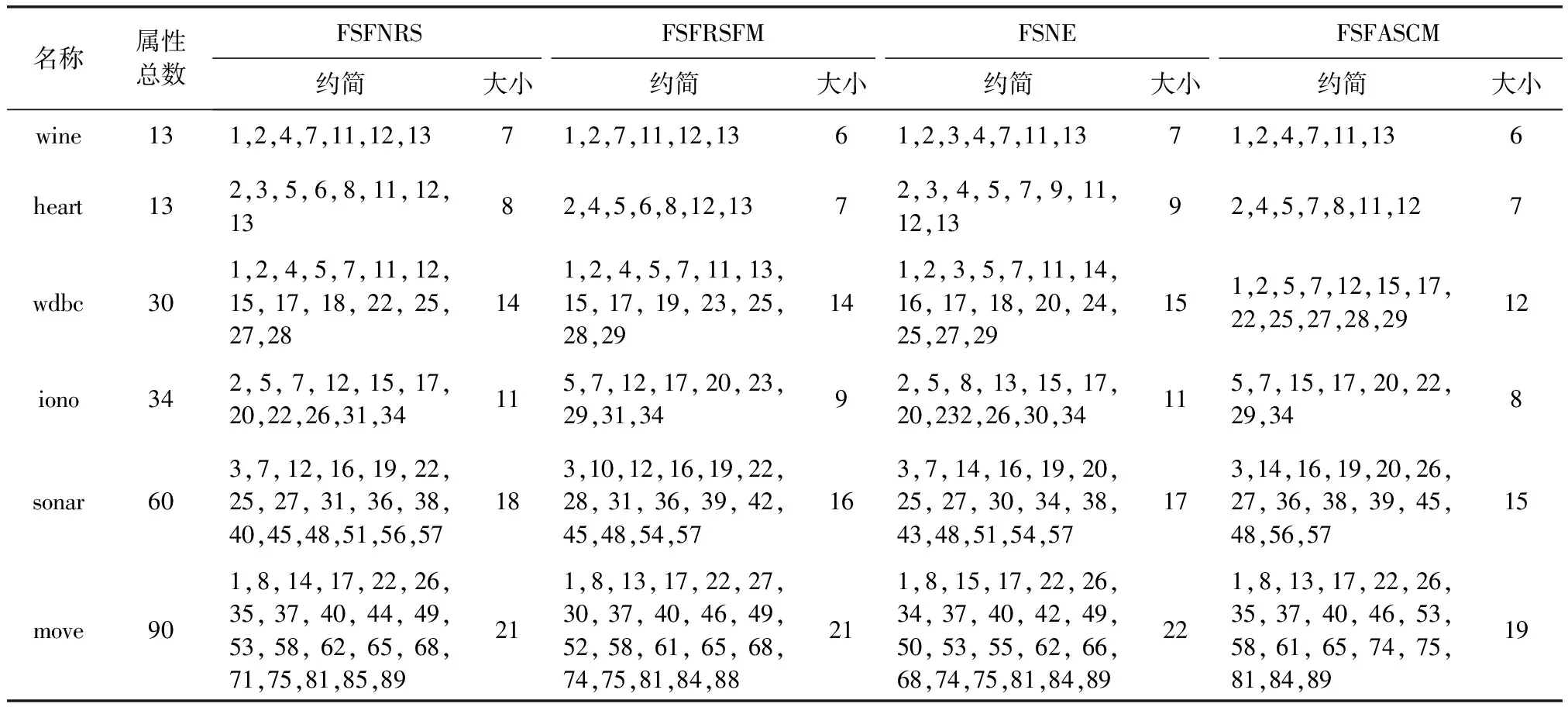
表2 4种算法的特征选择结果

接下来比较这4种算法在各个数据集上特征选择的算法效率。这4种算法的时间复杂度均为O(c2·n2)，我们将每种算法在各个数据集重复特征选择5次，算法的最终用时采用这5次时间的平均值，其实验结果如图1所示。

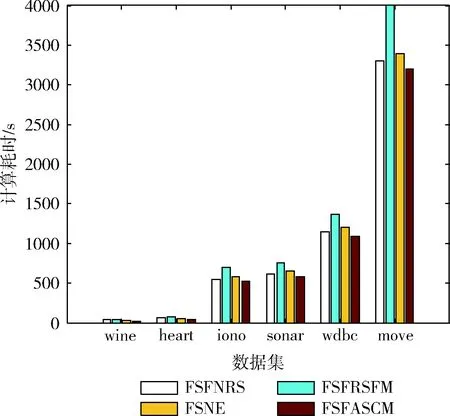
图1 4种算法计算时间对比

观察图1可以发现，虽然4种算法拥有相同的时间复杂度，但是具体的实验耗时略有差异，其中FSFRSFM算法在各个数据集上的实验耗时最长，而FSFASCM算法在各个数据集上的实验耗时是最短的，说明本文所提出的特征选择算法拥有了较高的计算效率。为了验证4种算法特征选择结果的优越性，实验中采用SVM和C4.5两种分类器分别对表2中的特征子集进行十折交叉训练，得到对应的分类精度，其结果见表3。观察可以发现，对于SVM分类器下特征子集的分类精度，除数据集heart和iono外，FSFASCM在其余数据集上的分类精度是最大的，说明了FSFASCM选择出更小的特征子集同时且保持高的分类精度。同时观察C4.5的分类精度结果，我们也能够得到同样的结论。通过以上实验分析可以看出，本文所提出的FSFASCM算法在特征子集大小、算法运算效率和分类精度方面均具有一定的优势，因而用于数据的特征选择是适用的。

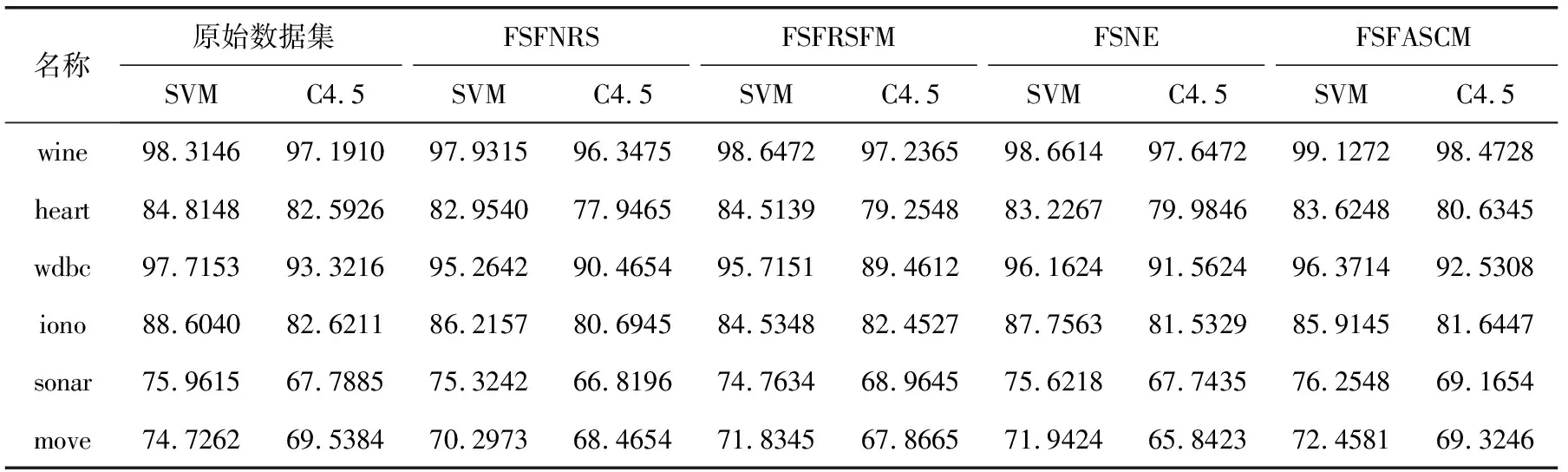
表3 4种算法特征选择结果两种分类器下的分类精度/%

5 结束语

由于现实中的数据集存在大量的不相关属性，因此对数据进行特征选择是很有必要的，本文在模糊近似空间引入模糊粒度，并在该空间中定义了模糊条件熵的概念，由于这两种方法是根据不同的视角来对属性进行重要度评估，因此将它们结合提出一种组合度量方法，同时给出相应的特征选择算法。UCI实验结果表明该算法的优越性。由于该特征选择算法适用于数值型属性，因而如何构造混合数据的特征选择方法将是接下来的进一步研究方向。