基于距离优化和改进粒子群的节点定位算法

张 溪，毛永毅，徐 萍

(1.西安邮电大学 电子工程学院，陕西 西安 710061；2.火箭军工程大学 理学院，陕西 西安 710025)

0 引 言

在无线传感器网络定位技术的两大分类中，基于测距的定位算法需要额外的硬件支持才能获取所需信息，而无需测距的定位算法依赖于网络间的连通和跳数值信息，其设备简单、功耗低、效率高[1-3]。

DV-Hop算法作为一种易实现的典型无需测距算法被广泛应用于无线传感网络定位中[4]，对于该算法定位精度不高这一问题，学者们不断探索并尝试改进。文献[5]用高斯牛顿法替代定位阶段的最小二乘法，减少误差传播。文献[6]利用跳距误差和估计距离误差的加权平均值去修正平均跳距，并引入改进粒子群算法计算未知节点坐标。文献[7]中对来自多个锚节点的跳数值进行加权操作用于平均跳距离的估计。文献[8]使用节点间最小跳数值和锚节点的位置信息，通过细菌觅食优化算法计算平均距离，使跳距误差尽可能小。

各类改进算法的侧重点在于减小估计距离误差和尽可能避免定位阶段误差的累积。因此，本文算法通过对节点间距离的优化和改进的自适应粒子群算法对DV-Hop算法进行改进，仿真结果表明，本文DPDV-Hop算法较原始DV-Hop算法和文献[6]中的BDV-Hop算法在定位精度方面有更优异的表现。

1 DPDV-Hop算法

1.1 估计距离优化

节点间估计距离是由平均跳距与跳数值的乘积所决定的，因此平均跳距的误差将直接影响估计距离的精确度。为了能使估计距离的误差减小，利用锚节点间单跳平均误差对平均跳距进行修正，使之接近真实值。估计距离的最终结果与平均跳距的选取方式存在一定关系，接收网通范围内所有锚节点平均跳距并参与运算的策略，能考虑全局信息使估计距离得以优化。

1.1.1 平均跳距修正

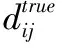
(1)

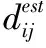
(2)

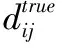
(3)

锚节点i的单跳平均误差可由式(4)计算得出，其中n为锚节点个数

(4)

(5)

1.1.2 多锚节点平均跳距估计距离

在估计节点间距离阶段，DV-Hop算法中待求未知节点根据就近原则只接收锚节点传递过来的第一个平均跳距信息。然而网络分布是具有随机性的，数据的单一选择不可避免的增加了偶然性，以至于影响后期定位。尽可能多地使用网络中信息即求到哪一点的估计距离用该点的平均跳距，不仅能考虑到全局信息而且在一定程度上降低了偶然性，使定位精度有所改善。

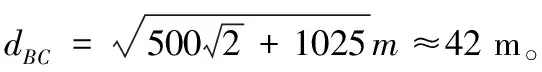
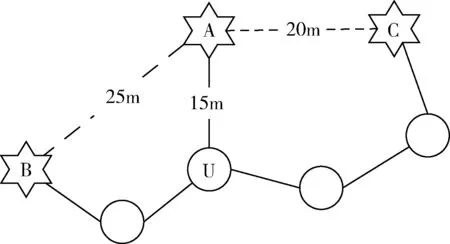
图1 网络拓扑结构

各节点平均跳距

HopSizeA=(25+20)/(3+4)≈6.428 mHopSizeB=(25+42)/(3+5)≈8.375 mHopSizeC=(20+42)/(4+5)≈6.888 m

使用各节点平均跳距通过不同策略估算节点间距离，结果见表1。

表1 节点间实际距离与估计距离

观察表1发现，提出策略能使估计距离更接近真实值。

1.2 改进的粒子群算法MI-PSO

1.2.1 粒子群优化算法

粒子群优化(particle swarm optimization，PSO)算法被Kennedy和Eberhart提出[9]。作为一种基于人口的元启发式搜索算法，它模拟了鸟类和鱼类在寻找食物方面的协作行为[10]。PSO算法中的每个人(即粒子)表示优化问题的潜在解决方案，而食物源的位置就是全局最优解。每个粒子相互独立并随机的寻找食物，它们之间还彼此协作和共享信息，通过不断地搜索寻求问题的最优解。

若目标搜索空间为D维，初始粒子数量为N，则粒子位置矢量可表示为Si=(si1,si2,…siN)，i=1,2,…,N， 粒子速度矢量可表示为Vi=(vi1,vi2,…viD)。 第i颗粒子现阶段所处的最优位置可表示为pi=(pi1,pi2,…,piN)， 整个种群的最优位置可表示为pg=(pg1,pg2,…,pgN)。 在每一轮的更新中，粒子对比这两个极值来改变自己的位置和速度，如式(6)所示

(6)

式中：k为粒子当前迭代次数；ω为惯性权重；c1、c2为加速度常数；r1、r2为(0，1)内的随机常数。

1.2.2 基于成功率PS的自适应惯性权重策略

通常式(6)中的惯性权重ω为一常数，ω越大则越利于全局寻优值，ω越小则越利于局部寻优值。为兼顾全局和局部寻优，提出自适应惯性权重策略。

实现自适应权重策略的重要之处在于每次迭代完成时需合理评估群体的位置。而本文提出的粒子成功率PS能表现群体现状，较高的PS值表示粒子向最佳解决方案靠近，并处于收敛状态，而较低的PS值意味着粒子在没有很大改进的情况下徘徊于最佳解决方案附近。因此，将粒子的成功率PS用于自适应地更新速度能有效提升收敛速度。使用粒子面向最佳解决方案的成功计数SC来确定PS的值。若当前迭代的适应度小于前一次迭代的适应度，则将SC值设置为1，否则将其设置为0，如式(7)所示

(7)

将所有的SC计数累加求和并由式(8)计算出成功率PS，其中N表示粒子数量

(8)

自适应惯性权重因子ω的设置如式(9)所示，粒子根据百分比形式的成功率自适应地更新惯性权重

ω=(ωmax-ωmin)×PS+ωmin

(9)

惯性权重(ωminωmax)的范围被设为[0，1]。因为PS为成功率，它的值总是在0～1之间，这就使惯性重量在可接受范围内。

1.2.3 变异算子参与运算策略

在PSO算法的执行过程中，粒子总是向最优解靠拢。若这一最优解为局部最优解，随着粒子的逐渐聚集，粒子便难以趋近于全局最优解，导致过早收敛即早熟现象[11]。

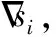
(10)

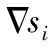
1.2.4 适应度函数设置

尽管在文章1.1节对节点间估计距离有所优化，但其误差并没有完全消除，考虑到估计距离所携带的误差，得到式(11)，其中εi,i=1,2,…n表示距离误差

(11)

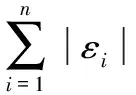
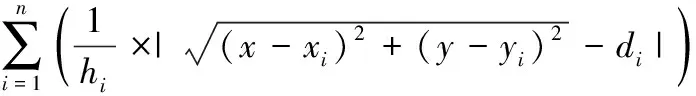
(12)

通过多次迭代使fitness(x,y)的值最小，以提升定位精度。

2 DPDV-Hop算法流程

步骤1 锚节点利用洪泛机制向全网广播自身信息，根据锚节点所获取的位置信息和最小跳数值计算平均跳距。

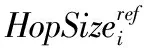
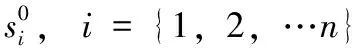
步骤4 若粒子si的变异概率Pc>rand(0～1)， 则执行步骤5，否则执行步骤6。

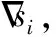
步骤6 比较更新后各粒子本次与上次的适应度值，由式(7)、式(8)计算成功率PS并带入式(9)中更新权重ω。记录本次迭代的个体最优位置pi和历史最优位置pg。

步骤7 将步骤6计算出的权重带入式(6)，用于对速度和位置的更新。

重复步骤4～步骤7直到达到最大迭代次数，输出最优适应度值及对应的粒子位置。

3 仿真实验

为了验证改进算法的性能，在Windows7的MATLAB R2014a环境下进行仿真实验。将拥有相同通信半径的100个节点随机分布在边长为100 m的二维方形区域内，如图2所示，其中○代表未知节点，*代表锚节点。初始化粒子个数N为30，最大迭代次数itmax为100。

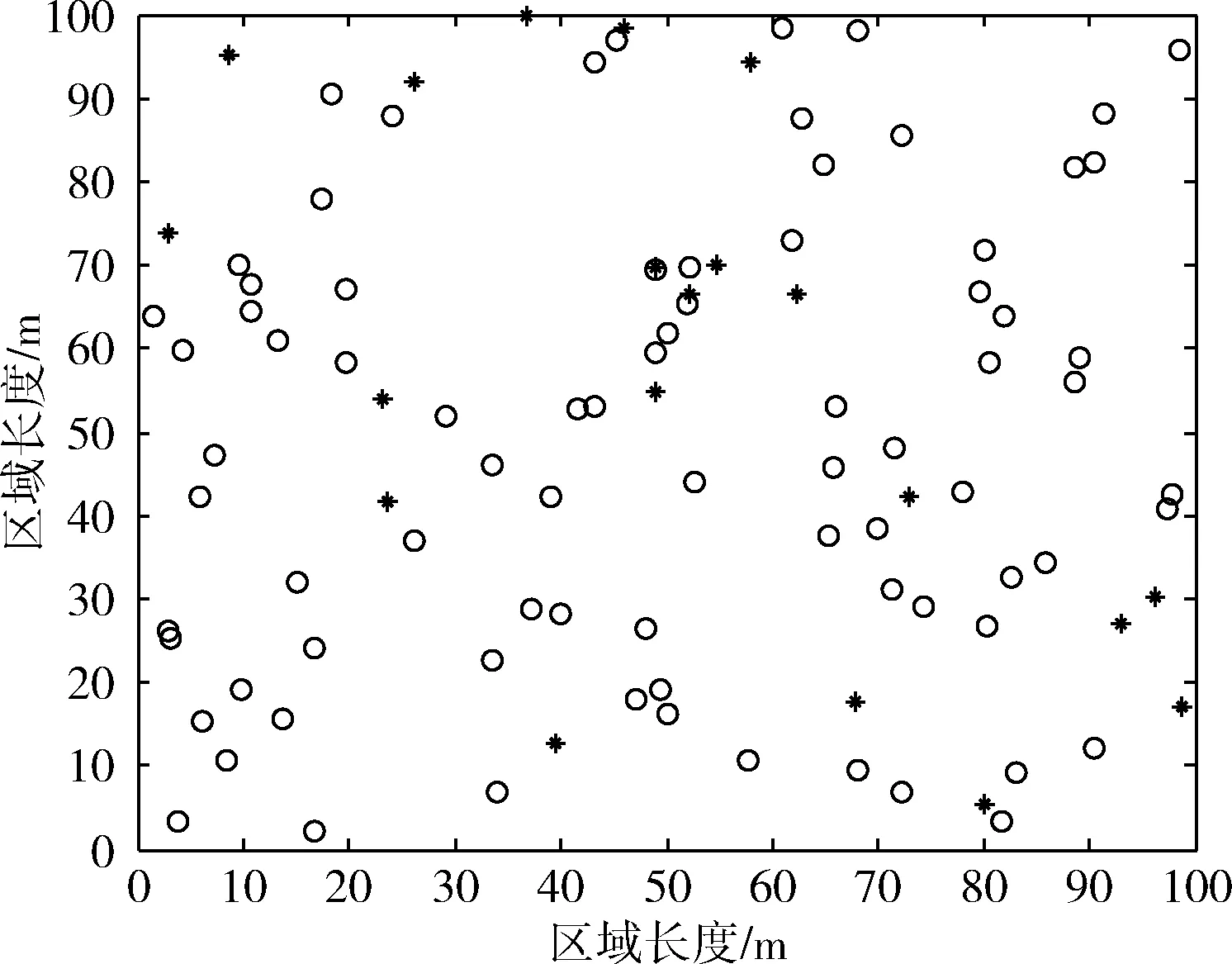
图2 节点分布

采用归一化相对误差作为性能评价指标，如式(13)所示

(13)

式中：(xr,yr)表示未知节点的真实坐标，(xi,yi)表示未知节点的估计坐标，R表示节点的通信半径，N表示未知节点数。

就DPDV-Hop算法本身而言，在对距离优化的同时也利用I-PSO算法替代了定位阶段的最大似然估计法。为了验证这两方面的改进均对定位精度的提升有所帮助，对DPDV-Hop算法分步仿真。当锚节点数占未知节点数量的20%，通信半径逐渐增加时，观察每个改进点在上述实验环境和初始条件下的定位表现。

图3表示锚节点数为20，分步加入距离优化和I-PSO算法后，通信半径从20 m～50 m的平均定位误差曲线。观察发现，通信半径从20 m～40 m这一阶段3条曲线整体呈下降趋势，这是由于网络连通度提升所导致的，而在半径大于40 m后表现出的上升趋势，是由于过大的通信半径使平均跳距误差增大带来的影响。因此，不必一味要求过大的通信半径，应合理选取。且这两个方面改进均降低了算法的定位误差，在加入I-PSO算法后的效果尤为明显，故DPDV-Hop算法是可行的。

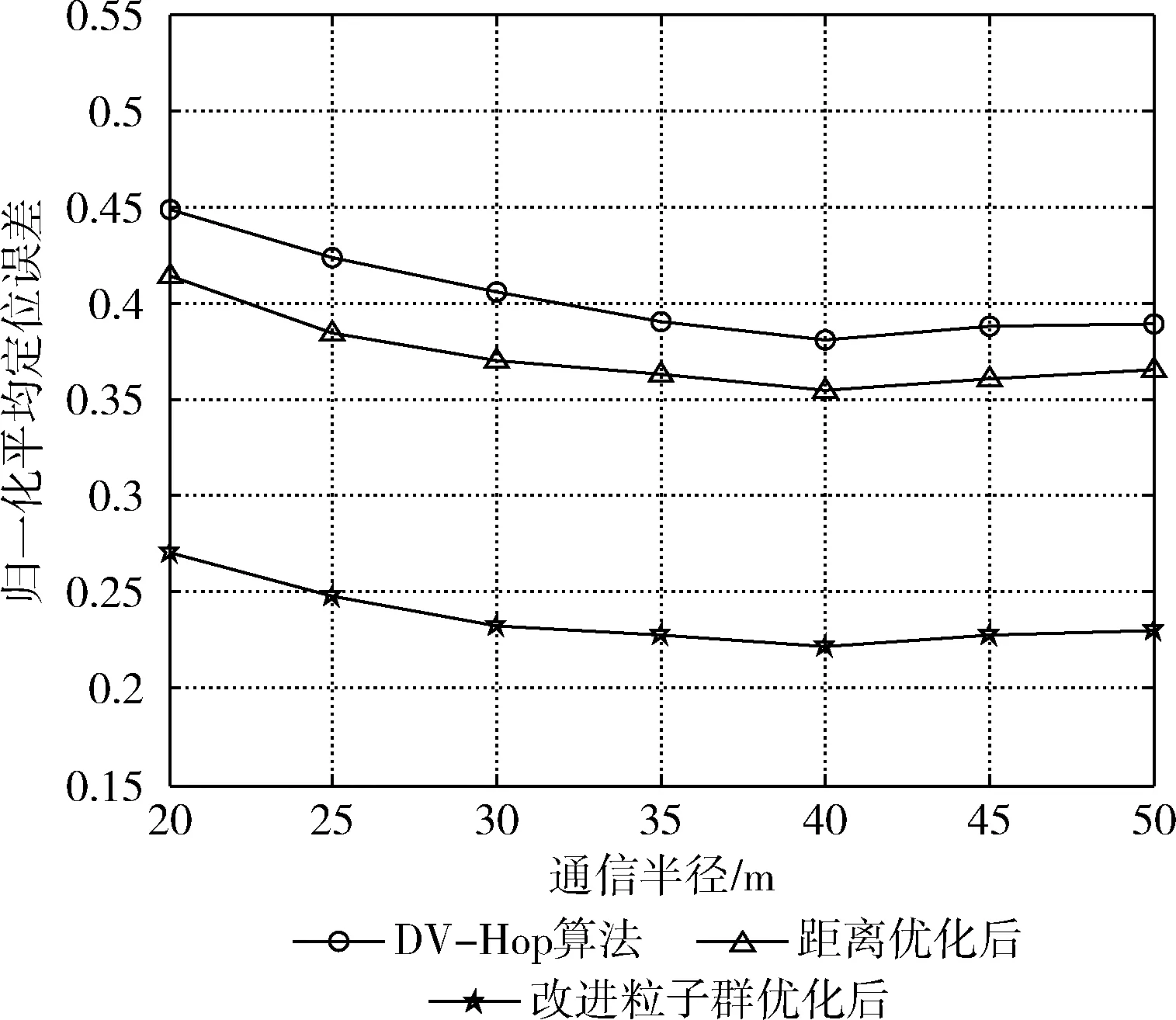
图3 通信半径不同时平均定位误差曲线

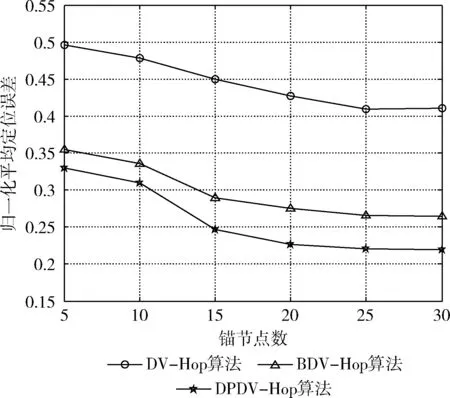
图4 锚节点数不同时平均定位误差曲线

为了验证DPDV-Hop算法的优越性，在不同锚节点数、通信半径下，对DV-Hop算法、文献[6]中的BDV-Hop算法与本文DPDV-Hop算法分别进行仿真，对比结果给予分析。

(1)不同锚节点数

图4表示节点通信半径为30 m，锚节点数从5-30时3种算法的平均定位误差曲线。观察发现，3种算法的误差曲线随锚节点的增加而降低，在锚节点数小于20时下降尤为明显，之后趋于平稳。这是由于锚节点密度的增大使其之间的跳数减小，这就有效减小了因高跳数所带来的误差累积，减少了距离误差。经计算，DPDV-Hop算法的平均定位误差比BDV-Hop算法和DV-Hop算法分别相对减少了39.97%和13.58%。

(2)不同通信半径

图5表示锚节点数占总节点数20%情况下，通信半径从20 m～50 m时3种算法的平均定位误差曲线。观察发现，当通信半径小于40 m时3种算法的曲线均处于下降趋势，大于40 m后又缓慢上升，导致此现象的原因与图3所分析的原因一致。且从图5中可明显看出，DPDV-Hop算法在任何通信半径下的定位表现均优于与之对比的2种算法。经计算，不同通信半径下DPDV-Hop算法的平均定位误差比DV-Hop算法和BDV-Hop算法分别相对减少了40.56%和14.74%。

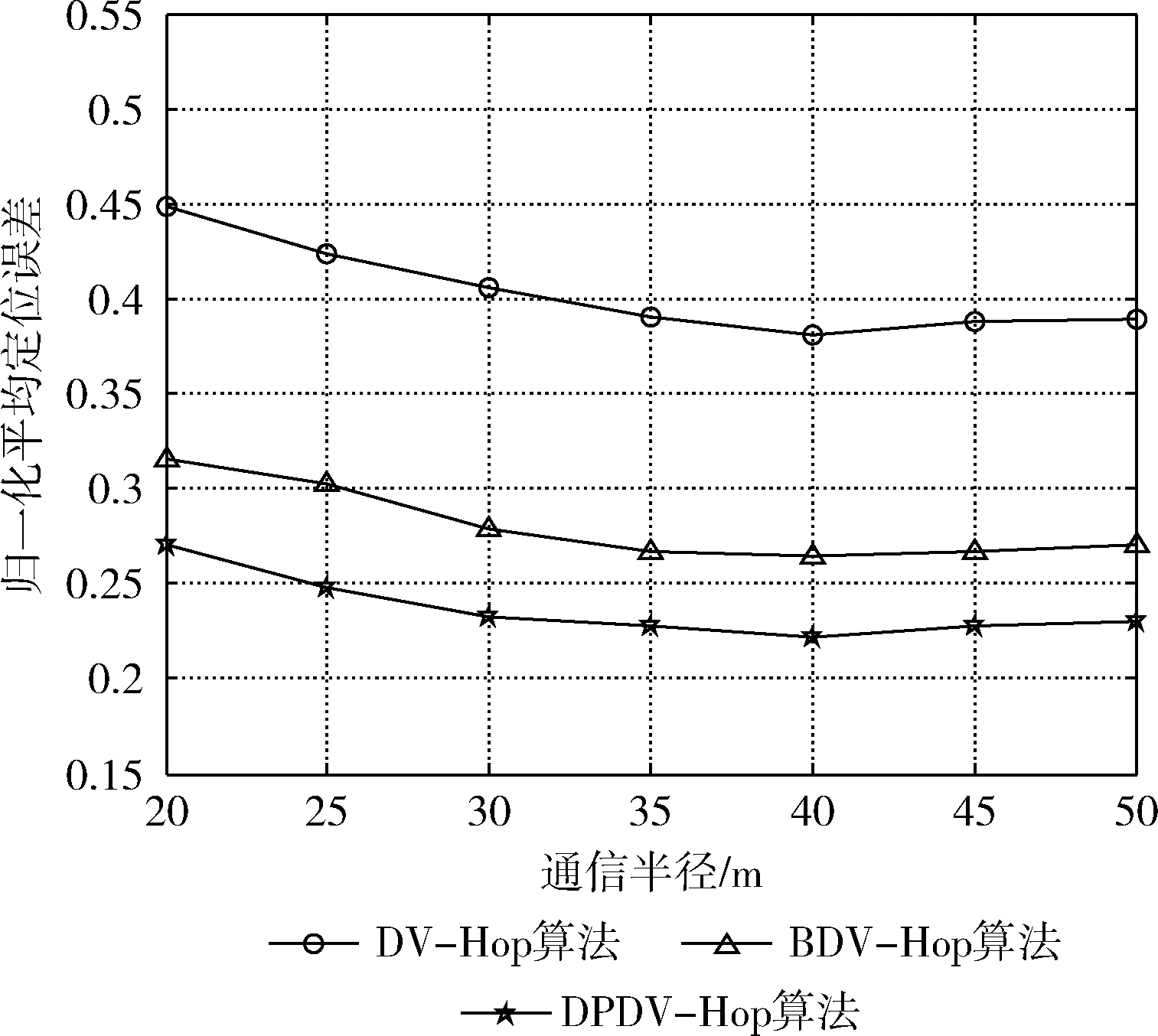
图5 通信半径不同时平均定位误差曲线

4 结束语

本文算法利用单跳平均误差修正了平均跳距，采用多锚节点平均跳距估计节点间距离，使估计距离得以优化。利用粒子成功率PS动态调节粒子群优化算法的惯性权重ω，加速收敛。产生变异算子并择优处理，避免早熟现象。用I-PSO算法的自适应迭代寻替代最大似然估计算法，降低了距离误差对最终定位的影响。仿真结果表明，本文算法在不增加硬件开销的基础上，提升了定位精度，适合在实际中应用。