砂卵石地层盾构施工引起的纵向地表变形预测*

孙海霞， 孔志鹏， 张　超

(沈阳工业大学 建筑与土木工程学院， 沈阳 110870)

自我国修建第一条地铁隧道至今的半个世纪里，我国已有四十余个城市已建、正建或筹建地铁.盾构施工法虽然具有施工高效、安全和适应力强等突出优点，被广泛应用于城市地铁轨道交通建设中，但仍不可避免地对周围土体产生扰动影响，并直观地表现为地表沉降或隆起.

目前根据已有的研究成果，国内外学者提出的盾构隧道沉降变形计算方法主要有经验公式法、理论解析预测法[1-2]、模型试验预测法[3]、神经网络预测法[4]、随机介质预测法[5]和有限元数值分析法[6]等.有限元数值分析法虽然能较好地反映岩土实际情况，但存在建立完全符合盾构施工工程实际情况的计算模型困难、计算过程中参数输入不准确等问题.在对地表变形预测方面，有限元数值分析更偏向于定性.而对于其他预测方法，一方面，只通过引入土体损失参量来考虑壁后注浆阶段的地面变形，未考虑注浆各参数对地面变形的影响；另一方面，大多数预测法只能解决二维平面内的地面变形预测，但盾构施工引起的地表沉降变形具有三维性和时效性等特点.

本文假定土体不排水，在砂卵石地层注浆浆液扩散半径[7]及注浆压力分布[8]研究的基础上，利用Mindlin解推导了同步注浆引起的地层三维变形计算公式，考虑地层损失、盾壳与围岩摩擦力对地表变形的影响，得到了砂卵石地层盾构隧道开挖引起的地表沉降计算公式.

1　盾构施工引起的地面变形分析

在盾构隧道开挖施工过程中，盾构通过土体所受到的力是复杂多样的，归结起来主要有开挖面推力、刀盘与土体摩擦力、盾壳与围岩间的摩擦力和同步注浆浆液压力[9-10].文献[2]指出土体开挖阶段的盾构开挖面推力对地层的影响较小，变形曲线如图1所示.

根据以上分析，盾构施工引起的总地表沉降变形可以通过先分别单独考虑盾构隧道同步注浆、地层损失和摩擦力引起的地表纵向沉降，然后将三个地表纵向变形量叠加求得.

本文假定：1)地层土体不排水固结；2)土体为线弹性半无限体；3)盾构的推进过程中不发生偏斜；4)同步注浆浆液为牛顿流体.

图1　盾构施工引起的纵向地面变形曲线Fig.1　　　　Longitudinal ground deformation curves induced by shield construction

2　地表纵向变形计算方法

2.1　同步注浆引起的纵向地面变形

2.1.1浆液压力引起的地层三维变形公式

图2为力学模型简图.任意取微元dA=Rdxdθ，并将其所受浆液集中力Pr沿水平与竖直方向分解为Ph=Prcosθ和Pv=Prsinθ.

图2　力学模型简图Fig.2　Simplified mechanical model diagram

利用文献[8]中在注浆扩散范围内任意点处的注浆压力计算公式，可以得出

(1)

式中：x为计算点到注浆口的水平距离在x轴方向上的投影；β为同步浆液与水的粘度之比；R为衬砌管片外径；θ为圆心角；φ=45°；r0为同步注浆孔半径；Pr为计算点处的注浆压力；Pg为注浆口压力；t为注浆时间；λ为浆液注入率；n为地层土体原始孔隙率；K为渗透系数.

将式(1)结果代入Mindlin解，积分得到同步注浆引起的地层三维变形计算公式.

1) 竖向分力Pv引起的地面变形为

(2)

(4)

2) 水平分力Ph引起的地面变形为

(5)

(6)

(7)

3) 总压力Pr引起的地面变形为

(8)

式中：R1=[(x+L+L0+s)2+(y-Rcosθ)2+(z-c)2]1/2；R2=[(x+L+s)2+(y-Rcosθ)2+(z+c)2]1/2；r为经过注浆时间t后浆液的扩散半径；G为地层土体剪切弹性模量；v为地层土体泊松比；c=h-rsinθ，h为隧道轴线距地表的距离；z为注浆口距地表的竖向距离；s为盾构机刀盘宽度.

2.1.2同步浆液的扩散半径计算公式

本文采用更适用于砂卵石土层渗透注浆的改进柱面注浆浆液扩散半径计算公式，即

(9)

式中：ρw为水的密度；ωw为水的运动粘度；σ为注浆压力水头；μ(t)为浆液粘度与时间的函数，其关系如表1所示.

表1　泥浆粘度与时间函数关系Tab.1　　　　Functional relationship between slurry viscosity and time

2.2　地层损失引起的纵向地面变形

图3为地层损失示意图.由图3可知，Sagaseta采用“镜像”法，利用圆柱体来等效模拟地层损失，得到地表竖向位移计算公式，即

(10)

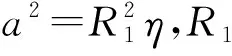
图3　地层损失示意图Fig.3　Schematic stratum loss

2.3　盾壳与周围土体间摩擦力引起的纵向地面变形

盾构机在土层顶进过程中，外壳与周围土体产生较大摩擦力.学者魏纲利用Mindlin公式，积分得到盾壳与周围土体摩擦力引起的纵向地面变形，即

(11)

表2　土体损失率的经验值Tab.2　Empirical values for soil loss ratio

式中：W=[(x+r)2+h2+R2-2Rhsinθ]1/2；p为盾壳与土体摩擦力.

2.4　总的纵向地面变形计算公式

将同步注浆浆液压力、盾构机外壳与周围土层间的摩擦力以及施工间隙引起的纵向地表沉降变形进行叠加，得到盾构施工引起的总的纵向地表沉降变形计算公式，即

w=wr+w1+w2

(12)

3　算例分析

为了验证本文理论，将理论计算值与现场监测值、Sagaseta理论值和有限元数值模拟计算结果进行比较.

以沈阳地铁某段为例，选取某区间DK6+761.680～DK6+797.680段，所穿越地层为典型砂卵石地层，其物理力学性质如表3所示.

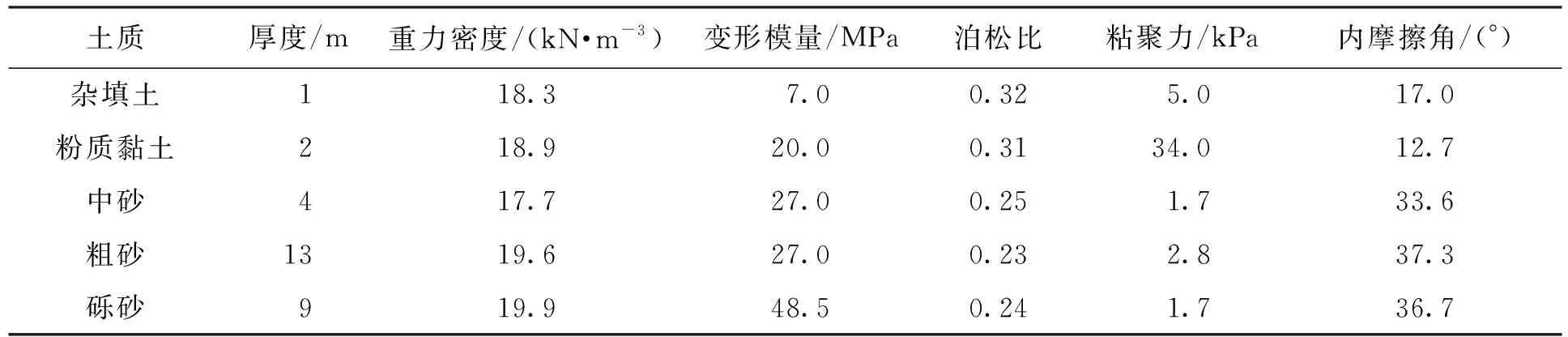
表3　物理力学性质Tab.3　Physical and mechanical properties

根据盾构隧道施工资料，参数取值如下：L=9.0 m，r0=0.025 m，R=3.0 m，R0=3.12 m，n=0.355，Pg=0.4 MPa，p=45 kPa，K=0.18 cm/s，t=120 min.由文献[9]可知，μ(t)=18.146e0.007 5t.将本文理论计算值分别与现场监测值、Sagaseta理论值和文献[11]中的数值模拟计算结果进行了对比，结果如图4所示.

由图4可知，在四种预测方法中，本文理论计算曲线与实际监测数据曲线更为吻合.理论计算的纵向地面变形曲线可以分为四个阶段：第一阶段，地面隆起阶段(见图4线③ab段)；第二阶段，沉降急剧增加阶段(见图4线③bc段)；第三阶段，沉降稳定阶段(见图4线③cd段)；第四阶段，沉降反弹阶段(见图4线③de段).该变化规律与文献[2，6]结果相同，即盾构开挖面到达计算点前一段距离时，地表进入隆起阶段；随着盾构开挖面的接近，地表由隆起变为沉降，纵向地表沉降值急剧增加，变形曲线进入第二阶段；在盾尾通过计算点一段距离后，纵向地面变形趋于稳定，之后达到沉降峰值；达到峰值后，纵向地表沉降产生反弹，曲线由第三阶段进入第四阶段即沉降反弹阶段.数值分析预测曲线未能反映出盾尾通过后的地表纵向沉降反弹现象；Sagaseta理论计算结果与纵向地表监测值相差较大；本文理论计算值反映了盾构通过时地表纵向变形的四个阶段，同时理论计算值与现场监测值较为吻合，绝对值误差范围在1.48%～12.72%之间，对比结果如表4所示.

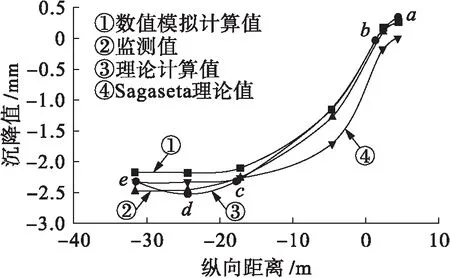
图4　预测值与监测值对比Fig.4　　　　Comparison between predicted and monitored values

监测点计算值/mm监测值/mm误差/%DK6+761.680-2.17-2.485.65DK6+768.880-2.18-2.453.56DK6+776.080-2.11-2.251.48DK6+788.610-1.17-1.288.91DK6+795.6100.160.103.06DK6+797.6800.240.2712.72

4　结　论

本文结合浆液在砂卵石土层中的扩散规律，利用Mindlin解推导了同步注浆引起的地层三维变形计算公式，考虑地层损失与摩擦力对地面变形的影响，得到了砂卵石地层盾构隧道开挖引起的地表变形计算公式.该方法考虑了多个施工参数，较数值模拟法更好地反映了地面变形的四个阶段，与工程监测数据更为吻合，能更好地符合砂卵石地层中盾构施工的实际情况.