挖掘算法在高速网络流频繁项计算中的实验应用

卢来，邓文，吴绍军，黄锦焕

（广东海洋大学寸金学院，湛江 524094）

0 引言

所谓高速网络流的频繁项数据挖掘是指在当前网络中海量的数据流中找出频率超出特定阈值的数据项。作为数据挖掘和数据流研究的重点工作，频繁项挖掘不仅关系到计算机专家对网络的管理，而且对于保障网络安全也具有重要影响[1]。数据流中最为典型的模型为网络流，对网络流进行分析可知，其除了具有一般数据流的动态流动且无法重演以及因数据量过多而无法全部保存等特点外，还具有报文的传输速率极高以及以少数的流项便可承担当前网络中绝大多数荷载的特点。基于上述特点，对网络流频繁项进行挖掘对于保障网络安全、规范网络管理具有重要的作用和意义。

本文通过提出一种基于时间与流长因素的网络流频繁项数据挖掘算法，即IWFIM，通过分析该方法的原理，进而提出了基于散列方法与计数方法二者优点的CBF-IWFIM算法，进而对两种算法对网络流频繁项的识别展开深入研究。

1 网络流的特性分析

由于频繁项算法的性能是由数据流的分布来直接决定的，而网络流又是数据流的一种典型表现形式，故在进行频繁项算法设计前，有必要对网络流的特性展开分析。为了使所得网络流的特性具有一般数据流的特点，将研究对象确定为选取骨干链路1999-03-21以及2009-03-30和2011-08-013组流量数据集，并以5元组方式将3组流量数据集的IP报文归并成数据流，在各组中随机选出10000条网络流作为分析对象，研究其相关特性[2]。经分析可知，网络流的持续时间t与流长l无明显现线性关系，而对于不同流长而言，其流的持续时间在分布上也较为分散。例如，椭圆区内网络流的持续时间不到整个网络流测量周期的1/2，而处于椭圆区内的网络流在处于1/2以上测量周期中并未接收到相关的数据报文。而对于矩形区的网络流而言，其流速虽然比较缓慢，但由于该部分流具有较长的持续时间，使得矩形区的网络流会随着持续时间的增加而逐渐成为大流。对上述椭圆区和矩形区的网络流进行分析可知，虽然二者在整个测量周期中都具有相近的流长，但若设定具体的时间段，研究2中IP流在特定时间段内的流长，将可能出现较大差异。由此可知，在对网络流频繁项的挖掘算法进行计算时，需要将流长、流的时间以及流速等方面因素进行综合考虑。

2 IWFIM算法设计与分析

2.1 原理分析

对网络流的特点进行分析可知，流长越大，则此流流长超过阈值进而成为网络流频繁项的可能性就越大。此外，区域内，流的时间越新，在该流的最近一段时间中，其获得网络数据报文的可能性就越大[3]。以此为基础，IWFIM将利用时时间与流长组合赋权的方法将每一个具体的流项赋权，而当当前网络流中的缓存为100%并此时有新流进入时，IWFIM算法总是将当前具有最小权值的网络流项。由于此时，数据流对计算机和当前网络的缓存占用同收到报文的数量极为紧密，故本算法以达到的报文在整个网络中的序号对网络流的时间因素进行描述。

设 IWFIM 中 F=＜ID，f，weight＞，其中 5 元组用 ID 来表示，f为网络流F的长度，流的权值表示为weight[4]。需要说明的是weight为流长、时间分别为权重系数α与β的多项式之和，表示为weight=αf+βiF，式中，达到的报文在整个网络中的序号为达到的报文在整个网络中的序号为iF。若某一网络流Fhit中已有报文Xhit抵达，则Fhit的流长与权重经更新后表示如下：fhit=fhit+1，weight=αf+βi，（f=fhit）值得注意的是如果所抵达的报文Xhit并未命中网络流频繁项数据挖掘算法即IWFIM算法中的任何流，则应新建流项 Fnew=＜IDhit，1，αf+βi＞。由于网络流中的短流占据全部网络流数的半数以上，故为了尽量避免后期所出现的某一单报文流便可将前期一个较大的流项淘汰的情况，有且仅有新流Fnew的权值超过IWFIM算法中缓存流的最小权值时，采用Fnew替换原IWFIM算法中缓存的最小权值流项[5]。

由于网络流频繁项的另一特点为不同流的持续时间也具有较大差异，且多半大流的持续时间较少（未达到整个测量周期的1/2），故此类流若在小于半个测量周期内便结束，则在后半个测量周期内，其权值始终保持不变。又由于后到达的新流Fnew初始权重的变化与其时间的变化呈现出显著的正相关，即新流权重岁时间的延长而不断增加[6]。因此，即便后期到达的新流流长较小，若流到达的时间间隔足够大，后期到达的新流权值也将超过前半个测量周期中大流的权值，进而将其淘汰出流的缓存空间，故在利用IWFIM算法时，需要先对前期所识别出的大流进行保护。

2.2 算法分析

IWFIM将网络中的全部缓存空间划分为P与M，其中算法所识别出的频繁项流以缓存P进行保存（初始值为0）。当缓存M中出现大于阈值的大流T流时，缓存P+1，M-1，并将T由M转移到P中[7]。M缓存以时间与流长组合赋权的方式将网络流中的频繁项进行挖掘，缓存M每进行1次剪枝操作，便将权值最小的流项删除。

对IWFIM算法的参数进行选择如下：由于权值weight=αf+βi，对于同一个网络流项而言，若α与β的取值不同，则该流的权值也有所不同，且IWFIM剪枝操作的顺序也不完全相同。具体来说就是，α与β的取值会对IWFIM算法的性能产生直接影响，且此算法下剪枝操作的顺序与各个流项的权值大小的排列次序相关联，且与各流项的具体权值大小无关，这表示在IWFIM算法中，剪枝操作并不受α与β同时扩大或缩小相应的倍数的影响[8]。由于在并不知晓网络流量具体分布的前提下很难找到一个β值进而保证IWFIM算法所提取的网络流频繁项效果最好，故本文在确定β值方面采取一种启发式的原理，利用网络中新到流的权值要略大于各流项的平均权值。因此，新到的流总是可以替换出缓存内具有较小平均流长的流。以l表示该算法的表项数量，若β=1/l，则新到流权值表示为weightnew=1+1/l，由此可知，新到流Fnew的权值weightnew要比平均流大，故能够满足要求，进而将参数β确定为β=1/l。

对此算法进行复杂度的分析如下：在IWFIM算法中如以散列的方法对报文的位置进行查找，则所查找报文的时间的复杂度和缓存P中网络流更新的复杂度均为O（l）。此外，缓存M中命中流项权值时间及流长的复杂度也为O（l）。当缓存P与M中均未命中新到流项Fnew时，则需要从M中找出当前具有最小权值weightmin的流项，其时间的复杂度为 O（l2）[9]。由此可知，在IWFIM算法中，报文时间复杂度最差，即最复杂时为 O（l2），最优为 O（1）。

3 CBF-IWFIM算法设计与分析

3.1 原理分析

由第2节可知，与流相比，网络中的短流在总体的网络流中占有极高的比例，而需要说明的是当网络遭遇DDoS攻击即分布式拒绝服务攻击时，在较短的时间内网络中所出现的短流以急剧的速度增长，又由于以技术算法为主的频繁项挖掘算法的每一个流项所占据的网络缓存流量相同，故计数算法下的大部分流量都会被网络中的短流占据[10]。因此，在大量短流存在于缓存区的情况下，将会对频繁项挖掘算法的识别产生较大阻碍。综上所述，在有限的缓存区中将网络中的部分短流进行过滤，进而减少进入计数算法的流数，将会有效提高频繁项挖掘效果。为此，本文引入CBFIWFIM算法，即基于计数型布鲁姆过滤（CBF）的网络流频繁项挖掘算法（IWFIM）进而实现对网络流频繁项的挖掘工作。在将散列算法与计数算法各自优势进行有机结合的基础上，通过借助散列的方法将当前网络中需要进行频繁挖掘的流项数目尽可能地减少，并以计数算法将IP流信息进行有效保存，从而使当前网络中的部分短流因受到散列冲突而进入布鲁姆过滤器CBF，并由IWFIM算法将其淘汰。CBF-IWFIM算法的原理图如图1所示。

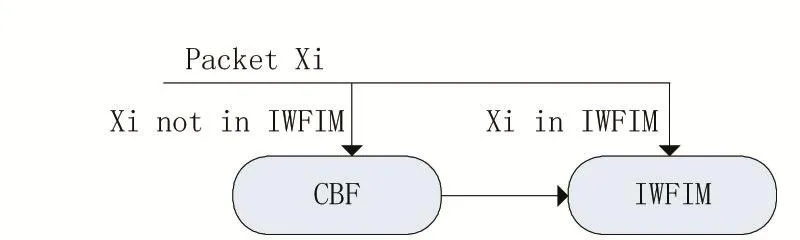
图1 CBF-IWFIM算法的原理图

在应用CBF-IWFIM算法时需要注意的是，因为网络中的短流（流长小于16）占据总体流数量的半数以上的比例，故基于计数型的CBF中的每个计数器的阈值TCBF设置为15即可。当CBF中每个计数器的值L=TCBF时，则判定为该流项已经通过CBF。又由于网络流中存在相应的散列冲突，故CBF的人过滤效果与其自身计数器的显示值呈现出显著的负相关关系，即过滤效果随着计数器数值的增加而逐渐减少，当CBF中所显示的计数器的值等于TCBF的NCBF的数量超过网络中短流数量N0时，布鲁姆过滤器将执行剪枝操作，即过滤器中的全部非0值均在原有的基础上减1。对于随新到流项Fnew而抵达的新报文Xi而言，首先需对其位置进行判断，并判断Xi是否在IWFIM中，若是，则继续利用IWFIM算法对Xi进行处理，若否，则通过CBF即布鲁姆过滤器对Xi进行处理。

3.2 算法分析

对CBF进行分析可知，由于其无需将IP流的5元组进行保存，且对与其相关的指针信息也无需保存，又由于每个计数器设置为4b即可，故基于CBF的网络流频繁项具有较高的空间利用率。对其挖掘网络频繁项的时间复杂度进行分析可知，相较于单一的IWFIM算法，CBF-IWFIM算法对于网络中不在IWFM的流项，还需添加计数器更新以及新的散列运算等相关操作，且操作时间的复杂度也大都为O（1），故在时间复杂度方面，两种算法对于网络频繁项的数据挖掘较为相似。

对CBF过滤器对网络中大流的影响做出如下分析。若在t时刻，CBF过滤器中有流项F通过，对于继F后到达的报文Xi，只要其与流项F中的前一报文Xi-1到达的时间间隔处于CBF-IWFIM两次剪枝操作的时间间隔之间，则对F本身进行分析可知，其存在着减1或不变两种可能。值得注意的是，无论流项F自减1还是保持不变，在CBF过滤器执行过滤操作后，均能够使F所影射的CBF过滤器中的k个计数器的值为TCBF，而过滤操作被执行的过程中，将不会对流项F的通过产生影响。由此可知，CBF-IWFIM算法对于网络中大流通过所造成的影响是较为有限的。

对CBF过滤器对网络中短流的影响做出如下分析。在忽略网络流项的散列冲突的前提下，流长l＜TCBF的流项并不能通过CBF过滤器。而由3.1中CBFIWFIM的原理可知，即便在存在散列冲突的情况下，高速网络中的短流通过了CBF过滤器，在IWFIM的作用下，其也会被立即淘汰，这也是CBF-IWFIM为什么不要求CBF过滤器将全部短流进行过滤的原因。而在网络中短流未通过CBF过滤器或已通过过滤器的短流被IWFIM算法淘汰时，CBF-IWFIM通过对CBF过滤器中计数器值为TCBF的计数器数量NCBF进行限制，进而确保过滤器中所产生散列冲突的概率可以被限定在有限区间内。由此可见，基于CBF-IWFIM的高速网络的频繁项数据挖掘算法可以即时过滤掉网络中的短流。具体算法如下：

输入：网络报文{X1，X2...Xn}，Xi=＜IDx，i＞。输入式中，报文Xi的5元组用IDx来表示，且Xi的序号用i来表示。

输出：IWFIM算法中缓存P的所有流项。具体步骤为：（1）当Xi到达时，对5元组进行查找，并确定IWFIM中是否存在IDx、，若存在，则调用IWFIM算法对此报文进行处理，若不存在，则跳转到下一步；（2）以散列算法将与5元组相对应的布鲁姆过滤器中的k个计数器计算出来，并对其中未达到TCBF的计数器加1，并对CBF中k个计数器的值是否均达到TCBF进行判断，若为True，则CBF允许Xi通过，若为false，则转入下一步；（3）对CBF中计数器的值为TCBF的数量NCBF进行统计，若其大于等于N0，则过滤器计数器的非0值均做减1操作，随机结束此次循环并等待下一个报文Xi+1到来。

4 实验分析与评价

4.1 实验材料

本次实验主要分为对数据的预处理以及频繁项的挖掘两方面。在数据的预处理方面，通过借助Plab开发包对网络流长、网络流的持续时间以及IP报文5元组等相关信息进行采集并记录，进而将此阶段所采集到的频繁项与网络流的流长共同作为算法效果的评估标准。在网络流频繁项的挖掘阶段，通过利用数学软件MATLAB在windows XP系统实现IWFIM与CBFIWFIM两种算法。本次实验所选取的网络流数据集为CAIDA所提供的一条型号为OC48链路的网络流量trace-2013与trace-2011。

4.2 基于IWFIM算法的参数设置

本次研究将网络流频繁项定义为出现频次大于1000的IP流。设Nt与Nf分别为正确检测出的大流数量与网络中误检测的大流数量，由IWFIM算法所检测出的大流流长于网络中原流长之间差的绝对值同原流长之比的平均值为本次实验的频数均差率E。由3.1中所述的IWFIM原理可知，IWFIM算法并不会出现将网络大流进行误报的情况，故参数Nf=0。通过实验可知，当表项数目l固定时，频数均差率E与大流数量Nt则分别存在着极小值与极大值，以Nt为例，当表项数目l分别为 6000、8000、10000 时，Nt的极大值分别位于β=1/l、β=1/10000（但与（Nt1/l）相差仅为 5）和β=1/11000（但与（Nt1/l）相差仅为3）。而对于频数均差率E而言，当l固定时，其具有较小的变化幅度，可忽略不计。由此可知，当表项数l固定时，IWFIM算法较为适合参数β=1/l的网络流频繁项的数据处理。

4.3 CBF-IWFIM算法的过滤效果分析

当利用CBF-IWFIM算法进行网络流频繁项挖掘时，将CBF中计数器的数量设置为N=214，并将4b设置成CBF计数器的位宽，设置散列函数数目k=3，N0=N/4，TCBF=15。将 CBF-IWFIM的表项数目l设置为10000，β=1/l。需要说明的是，由于在IWFIM算法中，每个网络流表项需要对流技术器、流指针以及IP5元组等信息进行保存。将每个流表项位宽设置为200b，则对CBF过滤器进行分析可知，过滤器占用的位宽不足500b。由此可知，CBF具有较高的空间利用率。

表1给出了CBF算法的原始流量信息以及到达IWFIM信息模块中的流量信息对比情况。

在实验过程中，通过对CBF-IWFIM算法的频繁项挖掘信息与IWFM算法的模块流量信息进行比较，进而得出CBF具有较好过滤效果的结论，进而说明了基于CBF-IWFIM的高速网络流频繁项数据挖掘算法可以在确保大多数网络报文得以正常通过的前提下，使IWFIM的表项数发生变化，即降低一个数量级，表明CBF可将网络中绝大多数的短流进行过滤，从而降低对计数算法处理的压力，并提高CBF-IWFIM中计数算法的频繁项挖掘效果。

5 结语

本文通过对高速网络流频繁项数据挖掘的概念进行阐述，在结合网络流的特性进行分析的基础上，从网络流频繁项数据挖掘的IWFIM算法与CBF-IWFIM算法两方面对其在高速网络流频繁项数据挖掘中的应用展开了实验分析。由本次实验可知，IWFIM所采用的流长与时间组合赋权值的方式实际上是对网络中的每个流项赋权，且在此算法下每次进行剪枝操作时，总是将具有最小权值的流项进行删除。而CBF-IWFIM算法所改进的布鲁姆过滤器将网络中的绝大多数的短流进行过滤，随后再采用IWFIM算法实现频繁项的数据挖掘。通过本次实验表明，IWFIM与CBF-IWFIM算法在告诉网络流频繁项数据挖掘计算方面均具有良好效果，且与IWFIM算法相比，CBF-IWFIM算法的空间利用率更高。可见，未来加强对挖掘算法在高速网络流频繁项计算中的应用研究对于保障网络安全提高网络管理效率具有重要的历史作用和现实意义。

表1 CBF-IWFIM过滤算法中CBF的过滤效果