壁面微结构流动控制技术的减阻机理研究
李恩田,吉庆丰,庞明军
(1.扬州大学 水利与能源动力工程学院,江苏 扬州 225127;2.常州大学 石油工程学院,江苏 常州 213016)
1 研究背景
流动控制技术是被动或主动采用某种装置使得壁面有界流动或自由剪切流动获得有益的改变,这些有益的改变包括减阻、增升、混合增强和流噪声抑制。壁面微结构减阻技术研究是近壁面湍流流动控制技术研究领域的一个重要组成部分,此项技术研究起步于上世纪30年代初,60年代中后期具有成效的研究工作普遍展开。Bechert等[1-3]对不同断面形状的壁面微结构做了大量试验,得到了相似的结论,V形微沟槽的减阻效果最好,当沟槽的高度h和间距s的无量纲尺寸分别为h+≤25和s+≤30时具有减阻特性,当h+=s+=15时减阻率最大,最大减阻率为8%。国内王晋军等[4-6]通过利用LDV、PIV流动测试技术发现:微结构壁面湍流边界层内部湍流强度减弱,并且边界层厚度增厚。黄桥高等[7]通过对脊状表面减阻的试验测量和数值模拟得出:脊状结构表面边界层流场涡结构中存在着“二次涡”,近壁区处黏性底层厚度比光滑壁面的要厚得多,湍流度显著降低。
以往的研究大多集中在具有壁面微结构的平板的外部流动,而对于管道内流动研究的比较少。Dean[8]通过压降测量的方式发现方形管道内肋条壁面微结构没有显著的减阻效果,但其试验并没有对边界层内部结构和对应的参数进一步测量。本文通过压降测量和粒子图像测速法(particle image velo⁃cimetry,PIV)相结合的方法来研究方形管道内壁面微结构的湍流减阻性能。通过压降测量初步确认壁面微结构的减阻性能,然后通过PIV测量出边界层内部结构和对应的参数,从机理上分析壁面微结构的减阻效果和性能。
2 试验装置
2.1水循环系统试验在水循环系统内进行,装置如图1所示。该循环系统包括方形测试管段、泵、流量计、差压变送器、收缩管段、扩张管段、稳流板和循环水罐等部分。方形管道用有机玻璃制成,测试段长2800 mm,方管横截面尺寸为100 mm✕60 mm。通过调节电机变频器来调节流量,利用差压变送器(量程0~3 kPa,测量误差±3 Pa)测量不同流量下测试管段的压降,通过电磁流量计(测量误差±0.01 m3/h)测量循环管路的流量。试验流体为普通自来水,水温控制在25±0.5℃。
试验所用方管段底面上的微结构为V形肋条和V形沟槽,是采用激光在有机玻璃平板上雕刻而成,肋条和沟槽顺流向布置。试验分别选取了相同沟宽(s)不同沟深(h)的3种沟槽和相同肋宽(s)不同肋深(h)的3种肋条,其结构与尺寸如图2和表1所示。
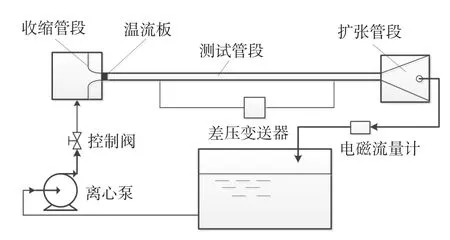
图1 试验装置示意图
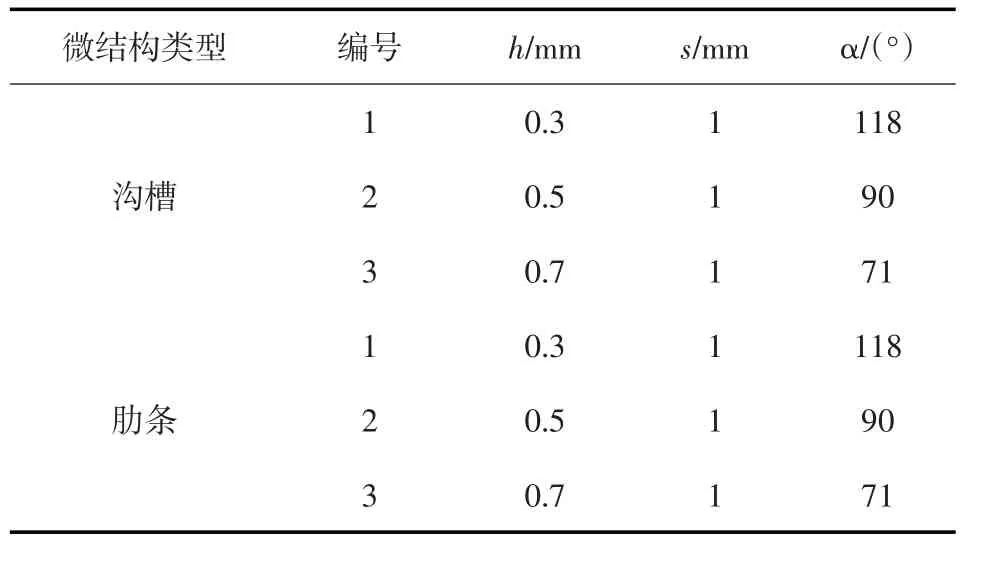
表1 微结构的尺寸
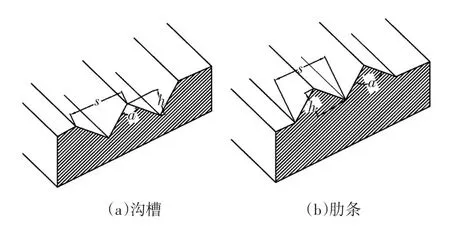
图2 壁面微结构示意图
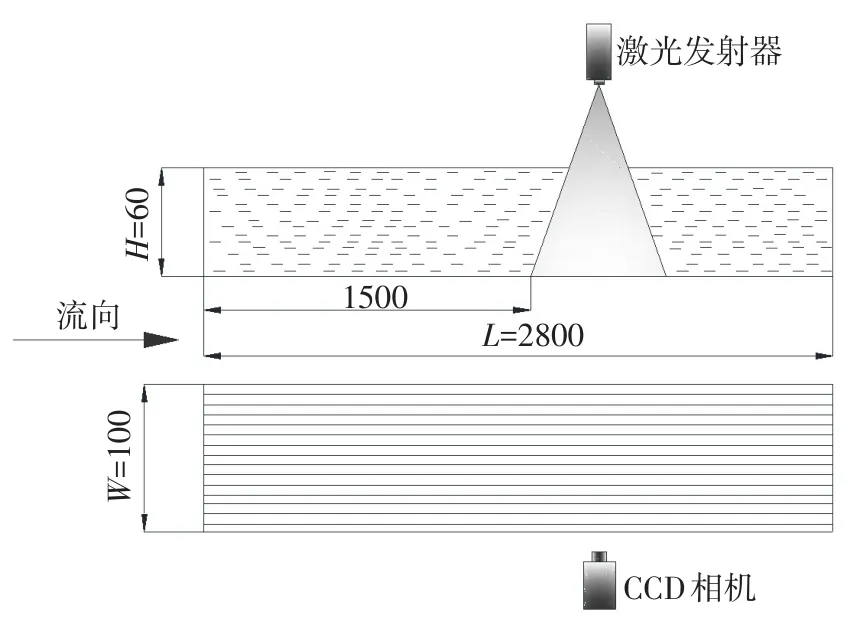
图3 PIV布置图(单位:mm)
2.2粒子图像测速仪本试验用到的PIV系统包括:双脉冲激光发射器、CCD相机、图像处理软件、激光臂和同步器。采用MicroVec软件对图像进行记录,利用tecplot软件对互相关处理后的数据进行分析。试验时激光片光源、CCD相机和平板相对位置见图3。拍摄过程中,激光片光源平面与平板垂直,与两侧壁平行,片光源位于矩形管道展向中心线处,CCD相机镜头与片光垂直。
PIV所用的激光器为KSP200系列双通道Nd:YAG激光器,最大工作频率为100 Hz,可见光波长532 nm,每个脉冲能量200 m J,脉冲宽度5 ns。CCD相机(ICDA-IPX-4M15-LMFN082702)分辨率1549×1697像素,微距镜头焦距为60 mm。采用tecplot软件对图像进行处理。本实验所测的流速中,对应的最小跨帧时间约为120μs判读区间有80%重合度,图像采集频率15 Hz。
3 试验结果与分析
3.1减阻率定义减阻率DR%:

式中:Cf0为光滑壁面的范宁系数;Cfw为肋条或沟槽壁面的范宁系数。
范宁系数Cf可由下式进行计算

式中:Δp为差压变送器所测得的测试管段压降,Pa;H,W,L分别为测试管段宽度、高度和长度,mm;ρ,U分别为流体密度和平均流速,kg/m3、m/s;
利用差压变送器测得的压降Δp、流量计测得的流量转换出的平均速度U以及测试管段的几何参数,由式(2)可计算出光滑壁面范宁系数Cf0以及肋条或沟槽壁面的范宁系数Cfw,代入式(1)即可得到肋条或沟槽壁面相对于光滑壁面的减阻率。
定义壁面微结构的无量纲宽度s+为

式中:u*为壁面摩擦速度,m/s;ν为流体的运动黏度,m2/s;关于u*的计算,可以根据文献[9]提到的方法进行计算。

如图4所示为本试验所测得的沟槽、肋条壁面减阻率及前人试验结果对比图。
从图4可以看出:沟槽、肋条壁面的减阻率与s+的关系均呈现相同趋势,即随着s+的增大减阻率先增大而后减小,当s+=15左右时,沟槽、肋条壁面减阻率达到最大值;对于沟槽壁面3和肋条壁面1、3,当s+>20时,壁面微结构不具有减阻效果,而对于沟槽2壁面和肋条壁面2,壁面微结构失去减阻效应发生在s+≈27之后。因此,当h/s=0.7,s+超过20时,沟槽壁面和肋条壁面都不具备减阻。比较本实验和Bechert[10]试验的结果发现:当h/s=0.5,s+在10~25时肋条壁面减阻率要比Bechert的研究结果大的多,Bechert试验最大减阻率约为3.42%,而本试验的最大减阻率为7.45%。其原因可能是由于试验的条件不同。首先,Bechert的试验是在二维明渠管道(尺寸:25 cm×85 cm)内进行的,并且它们用石油作为流体,而本试验是在三维压力管道(尺寸:6 cm×10 cm)内进行,并且以水作为流体;其次,Bechert的试验使用的肋条壁面其肋条之间有较大的间距,而本试验的肋条间无间距。综上分析可得,不同尺寸、不同形状的壁面微结构对管道的减阻情况影响很大。沟槽壁面减阻效果总体上要比肋条壁面理想,并且减阻范围(s+)也要比相应肋条壁面宽。表2给出了沟槽壁面与肋条壁面减阻情况的对比,沟槽壁面、肋条壁面减阻效果都要受h/s、s+以及流动工况的影响。
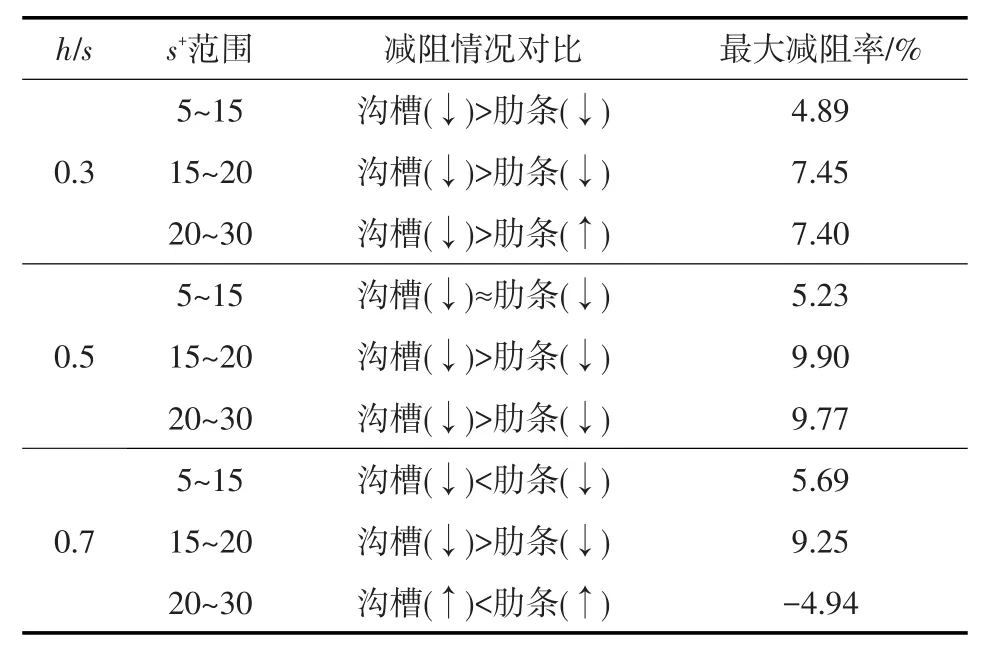
表2 沟槽壁面与肋条壁面减阻情况对比
3.2平均速度分布根据PIV技术所拍摄到的300个瞬时速度场经过时间平均、空间平均后得到的瞬时平均速度u数据,利用式(4)、式(5)算出来的无量纲平均速度u+,绘制出微结构壁面与光滑壁面湍流的无量纲平均速度u+和无量纲化法向坐标y+之间的关系曲线。如图5所示为Re=17 600(对应s+≈16)时流向平均速度剖面图。
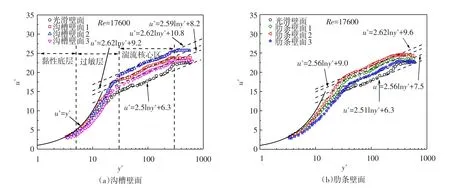
图5 流向平均速度剖面图
从图5可以看出,6种微结构壁面流向平均速度分布仍然符合“标准速度律”,即:

其中:A=1/k,B为常数,由试验确定,对于光滑壁面来讲,k=0.40;y表示任意点壁面的距离,m。
如图5,微结构壁面与光滑壁面流向无量纲速度分布分区现象特别明显:黏性子层(0<y+<5)、过渡层(5<y+<30)、对数律层或湍流核心区(30<y+<300);本试验测得的光滑壁面流向无量纲速度分布与理论公式相符:u+=y+(黏性子层),u+=2.5ln y++6.3(对数律层)。在黏性底层、过渡层里,微结构壁面与光滑壁面速度分布差异很小;在湍流核心区,微结构壁面的无量纲速度分布与光滑壁面无量纲速度分布差异明显,微结构壁面无量纲速度分布的对数区比光滑面的要明显上抬,A、B值都变大。
表3给出了s+≈16、7、28时,沟槽、肋条和光滑壁面壁面无量纲速度分布对数律中的A、B的值。由表可知,s+≈16、7时,沟槽、肋条壁面无量纲速度分布对数律区的A、B值比光滑壁面都相应增大,说明此工况下边界层增厚,流动阻力下降;当s+≈28时,沟槽、肋条壁面无量纲速度在对数律区的A、B值比光滑壁面的小,阻力反而增加了。这一结论与前面减阻率的结论是一致的。
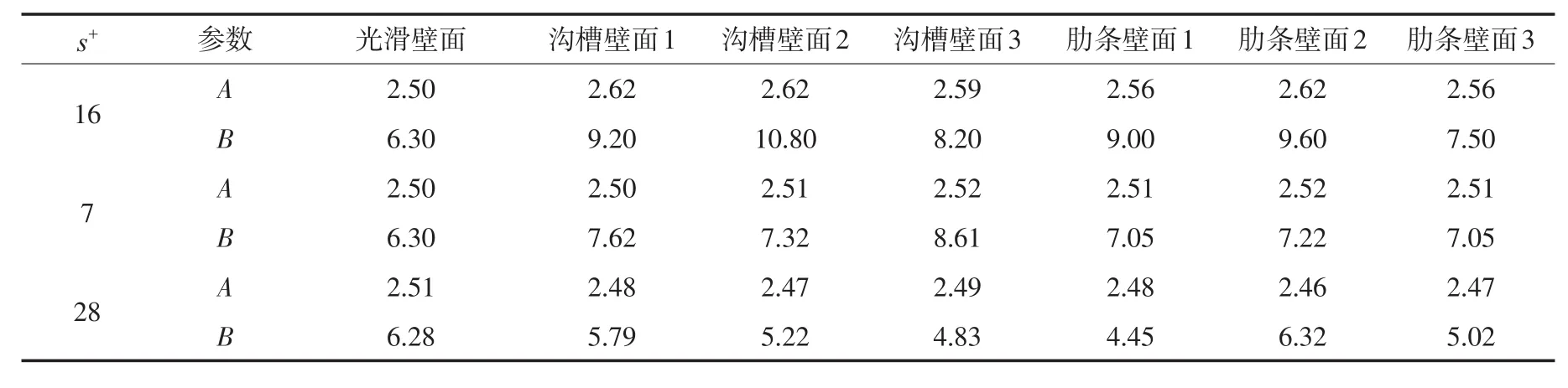
表3 对数律中A、B的值
3.3雷诺切应力雷诺应力的表达式为τij当i=j时,τij=σ=称为法向应力;当i≠ j时,τij称为雷诺切应力。本实验考察了雷诺切应力并使用壁面摩擦速度u*做了无量纲化处理,即图6所示为Re=17 400(对应s+≈16)时的雷诺切应力沿壁面法向分布。由图可知微结构壁面流向雷诺切应力分量在湍流边界层缓冲层区域及对数律区均有明显降低,之后又趋于一致;沟槽、肋条壁面流场内雷诺切应力最大值较光滑壁面管道小,其中,沟槽壁面2的雷诺应力最大值与光滑壁面最大值差异最大,沟槽壁面2比光滑壁面雷诺应力小16.58%。这是因为微结构限制了近壁区脉动,削弱了脉动速度和雷诺应力分量,从而减少了高速流体与低速流体的动量交换,使得微结构具有了减阻效果。

图6 雷诺切应力沿y+分布图
表4给出了不同工况下微结构壁面与光滑壁面最大流向雷诺应力的相对百分比,用Δ表示(如沟槽壁面1与光滑壁面最大流向雷诺应力的相对百分比为

表4 最大雷诺应力对比结果
3.4湍流强度湍流强度是用来衡量湍流强弱的相对指标,流向和法向湍流强度分别是式中u′和v′分别为流向和法向的脉动速度。使用壁面摩擦速度u*做了无量纲化处理,可得图7给出了Re=17 400(对应s+≈ 16)时,微结构壁面和光滑壁面流场内湍流强度Ⅰ的分布。由图可以看出,沟槽、肋条及光滑壁面管道流场湍流强度的变化趋势相同,在黏性子层(0<y+<5),湍流活动很弱(但仍然存在),随着y+的增大,湍流强度迅速增大,并且流向脉动速度与法向脉动速度均方根值在过渡层(5<y+<30)达到最大,之后湍流强度逐渐减弱。在黏性子层(0<y+<5),微结构壁面的湍流强度与光滑壁面湍流强度差异很小。过渡层(5<y+<30),微结构壁面流向速度均方根的最大值要比光滑壁面的小。此处也是高速、低速条带主要存在的区域[11],说明此种微结构在此工况下对条带生成、发展的抑制作用较大,减阻效果大。对比3种沟槽壁面流向与法向速度均方根最大值之间的关系,发现:肋条壁面也有相似的结论。这些都表明壁面微结构的存在使得流场内流向、法向速度均方根值减小,湍流强度减弱,从而实现了减阻。同时,从图7中可以观察到在湍流核心区或对数律层(30<y+<200)时,微结构壁面流向均方根速度对比光滑壁面管道呈现先大后小然后又大的情况,说明在对数率层速度均方根值与壁面结构、流速有很大的关系。最后,对同工况下同等尺寸不同结构的壁面流场进行比较,可以看出沟槽壁面对湍流强度的减弱效果要比肋条壁面大。
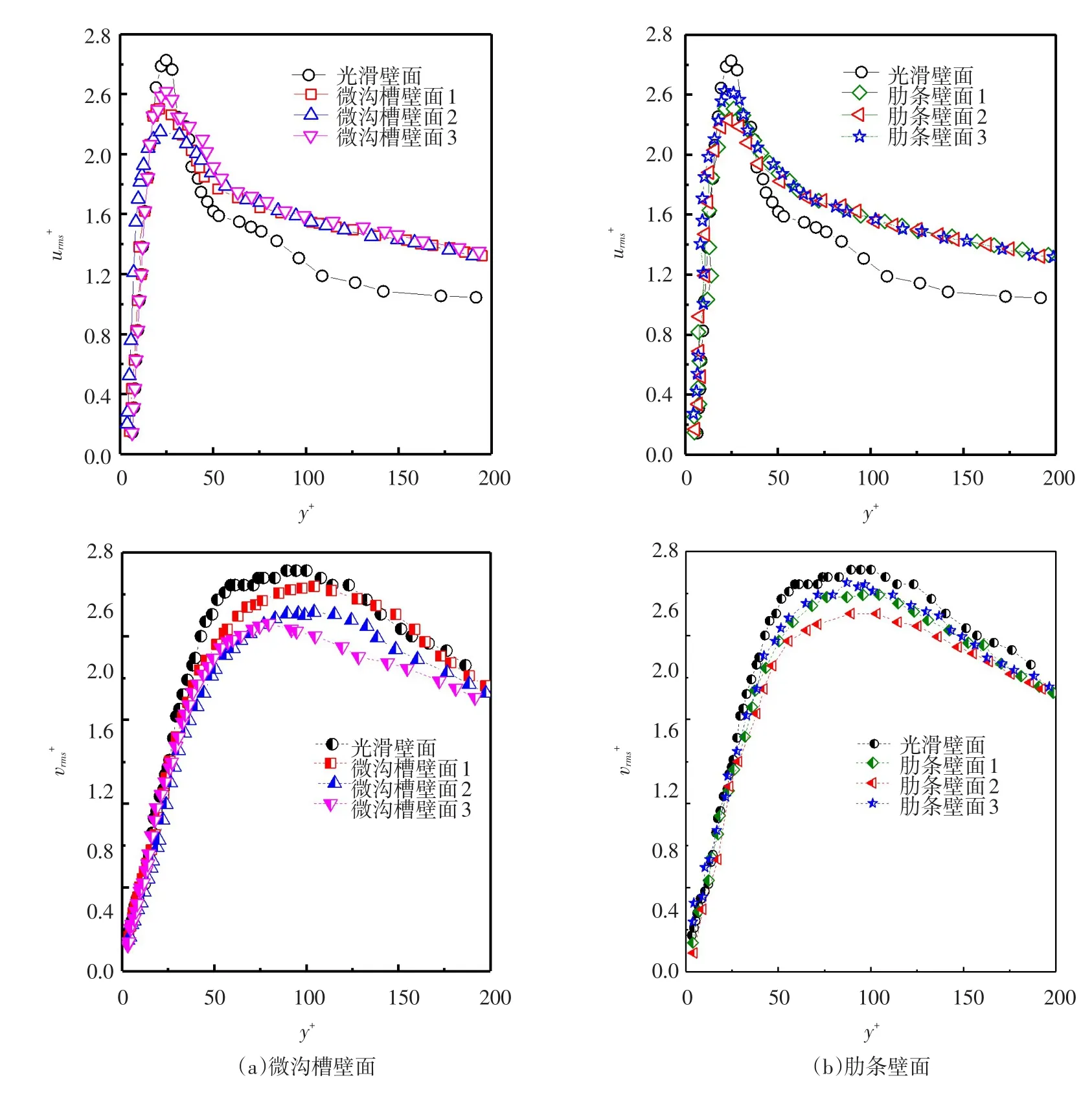
图7 均方根速度沿y+分布
3.5PIV测量的精度分析PIV系统的测量误差分析可以从系统误差和随机误差。但是在实际PIV系统中,由于存在复杂的光学系统、激光器系统、同步控制器、软件计算等等各个环节,很难明确的区分系统误差和随机误差;因此在实际评价PIV系统总的测量误差时,可以通过流场品质很好的水洞来实际校准PIV系统[12-13],董明哲等[14]提出了一种新的评价PIV系统测量误差的方法:利用匀速转动圆盘上粒子的反射光模拟流场中示踪粒子散射光解决基准速度场。另外,多年来大家都采用公认的蒙特卡罗数学方法(Monte Carlo simulations)来对PIV图像系统进行测量误差的分析。
4 减阻机理分析
壁面微结构是否具有减阻效应与流体的流动状态密切相关。当流体处于层流状态时,壁面微结构不具备减阻效应,甚至会增加流动阻力;而当流动状态处于湍流时,壁面微结构就有可能具有减阻效应。
4.1“突出高度”理论从表3可以看出,相较于光滑壁面,微结构壁面流向无量纲速度分布对数率中A、B值均有不同程度地增大,反映到边界层的结构就是其黏性子层相比光滑壁面增厚,即所谓的“突出高度”。Bechert等[1]研究认为这是由于微结构低谷内存在一种作用类似于润滑剂的流体,类似于将黏性子层的向远离壁面的方向移动使得此层的厚度增加,另外它们的存在使得流场中流向涡结构与壁面之间存在了距离,抑制了流向涡结构的演变过程,从而达到减阻的目的。
4.2“第二涡群”理论壁面微结构的减阻效果与“尖端效应”、“约束效应”两种基本现象有关[15-16],并且以上两种现象只在微结构壁面的流场中才存在,光滑壁面流场中并不存在。
以图4中的沟槽壁面2为例,分析这两种效应的作用结果。当s+<15时,壁面微沟槽减阻效果随着s+的增大而增强;特别当s+<10时,流体流速较小,雷诺数小,而湍流涡结构尺寸很大,对沟槽低谷流体与外部流体动量交换抑制较弱,此时壁面微沟槽的减阻效果较差,如图8(a);当10<s+<15时,壁面微沟槽减阻效果随着s+的增大而减弱,这是由于随着雷诺数的增大湍流强度增大,而壁面微沟槽对于沟槽尖端与沟谷动量交换的抑制增强,湍流脉动(u′、v′)增强,雷诺切应力增大,但壁面微沟槽“约束效应”的减阻效果仍大于“尖端效应”的增阻效果,所以最终壁面微沟槽仍呈现出减阻的效果,如图8(b);当s+≈15时,沟槽尖端与沟谷动量交换抑制作用达到最强,同时湍流脉动强度、雷诺切应力适宜,最终使得沟槽减阻效果达到最佳,如图8(c),同时在沟槽内形成了“第二涡群”,此涡结构的形成会抑制槽能流体与外部流团之间的动量交换,从而使得槽内流体的流动变得更加稳定,流动阻力减小,增强了壁面微沟槽的减阻效果。当s+≈22时,壁面微沟槽的减阻率值为0,表明“约束效应”的减阻效果与“尖端效应”的增阻效果相中和,壁面微沟槽没有减阻效果,对流场阻力总的影响效果与光滑壁面相同。当s+>22时,随着雷诺数的增大,湍流脉动进一步增强,沟槽尖端与沟谷动量交换频繁,涡结构增大,尺度变小,壁面微沟槽对管道起到了增阻的作用,如图8(d)。

图8 微沟槽壁面近壁区涡结构变化过程
5 结论
本研究对微结构壁面和光滑壁面作为底面的矩形管道的湍流特性进行了对比试验,通过对比分析减阻率、平均流速、雷诺应力和湍流强度等流动参数,得到如下结论:
(1)在一定的s+范围内,6种不同的微结构壁面都具有减阻效果。不同微结构壁面的减阻效果与h/s、s+相关。研究发现不同微结构壁面的减阻效果都随着s+的增大,呈现先增大后减小的趋势,其中沟槽壁面2的减阻效果最好,最大减阻率为9.90%;
(2)不同壁面微结构通过“尖端效应”及“约束效应”两种现象的相互作用,从而使得壁面微结构具有减阻或增阻效果。壁面微结构通过影响湍流脉动强度、雷诺切应力、平均流速等,从而使得壁面微结构具有减阻效果;
(3)微结构壁面的无量纲流向速度分布曲线对数率区的A、B值比光滑壁面的大,黏性底层相对于光滑壁面增厚。

