基于区间直觉模糊数TOPSIS法的患者满意度综合评价*
张利平 刘晓迪 张秀川 李望晨 刘建明
潍坊医学院“健康山东”重大社会风险预测与治理协同创新中心(261053)
【提 要】 目的 立足于模糊多属性综合评价问题,探索建模方案并阐述实施流程,以患者满意度评价问题为载体验证可行性。方法 以区间直觉模糊数测度多属性决策中的各属性隶属度、非隶属度范围。将对象各属性加权集结,计算与正、负理想对象的欧氏距离、相对贴近度,由此排序或择优。结果 以患者满意度调查及评价问题为案例,给出区间直觉模糊数决策矩阵,各属性隶属和非隶属区间数与“逼近理想解”法相结合,通过综合评价模型设计发现合理可行。结论 针对满意度评价等多属性模糊决策问题,该模型适用性能优良,理论流程及实施步骤对于卫生决策者有方法借鉴意义。
患者满意度是卫生服务质量监控和医疗行业竞争提升的影响因素,受到医院管理者重视,成为卫生评价或决策应用研究代表性问题。传统Fuzzy模糊数学法多见于综合评价研究,直觉模糊集作为改进方法,从隶属度、非隶属度和犹豫度来更充分描述或测度事物模糊本质。近年来学者继续提出区间直觉模糊集,以隶属度或非隶属度区间数来更合理测度模糊信息,基于区间直觉模糊集排序或择优方法受到关注。为此本文考虑以区间直觉模糊集和TOPSIS法为基础设计建模方案。以患者满意度综合评价为案例,阐述理论流程、制定计算步骤、验证可行性并讨论其应用价值,为卫生领域类似决策或评价问题提供方法借鉴。
研究方法
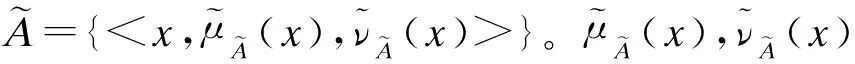
(1)
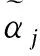
d(α1,α2)=
(2)
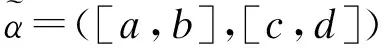
(3)

算法流程
1.基本思想传统且常见思想是将多对象组成集合,逐级细化为不同属性并以精确实数测度优劣。将属性值无量纲化并加权集结计算后将对象进行排序或择优。新的思想是将对象各属性值表示为隶属度和非隶属度区间模糊数,属性信息由集结算子加权合成为“综合区间模糊数”。经区间数向量或矩阵表示后,引入理想解逼近(TOPSIS)法,“远离负理想对象”且“靠近正理想对象”,之后依次计算“欧氏距离”和“相对贴近度”,将对象进行排序或择优。
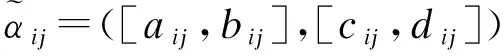
如此将对象{A1,A2,…,Am}关于属性{u1,u2,…,un}的区间直觉模糊数汇总为决策矩阵:
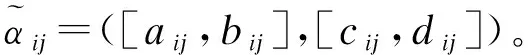
由公式(1)将Ai关于所有属性区间直觉模糊数加权集结为“综合”区间直觉模糊数:
按上述步骤,依次将{A1,A2,…,Am}计算出欧式距离及相对贴近度。
根据Ci大小对{A1,A2,…,Am}进行排序或择优;Ci越大则对象Ai越优。
若属性体系为二级层次树状结构形式,也可由公式(1)、(2) 和(3)从一级属性向二级属性逐步加权集结,并在相应层次内建模计算,将对象{A1,A2,…,Am}进行排序或择优。
案例实证
1.问题与资料立足于医院管理统计领域患者综合评价满意度问题[4-5],以案例为载体,以区间直觉模糊数、逼近理想解法(TOPSIS)等知识制定建模方案并验证可行性。
从门诊、住院维度细化患者满意度属性,门诊维度u1(0.45):{挂号候诊u11(0.34)、诊断检查u12(0.37)、挂号取药u13(0.29)};住院维度u2(0.55):{手术治疗u21(0.35)、康复护理u22(0.34)、出院指导u23(0.31)},括号内为权重。对各属性制定满意度评语集{“不满意”,“不算理想”,“说不清楚”,“还算可以”,“满意”},各属性附有内涵解释。由“不满意”和“不算理想”制定非隶属度;由“还算可以”和“很满意”制定隶属度。采用如下公式:满意隶属度=((“满意”数×2+“还算可以”数)/3)/ 总数;满意非隶属度=((“不满意”数×2+“不算理想”数)/3)/总数,总数=“满意”数×2+“不算理想”数+“说不清楚”数+“还算可以”数+“不满意”数×2,已剔除无效问卷。
调查地点为三所附属医院,每个季度3、6、9、12月最后一周内完成调查,由行政部门协调配合。调查员为研究生,调查对象为患者或家属,由门诊现场随机抽取或住院区病房床号抽样,经其知情同意后勾选作答,现场质控及逻辑检错。统计有效问卷中每个属性评语数,计算隶属或非隶属度。每次调查结果有差别,引入区间直觉模糊数来描述本年度该医院各属性满意度变化范围,合理反映其模糊认识。资料整理过程较繁琐,限于侧重点不再给出,现将该年度三所医院、各属性满意度区间直觉模糊数汇总,标记为决策矩阵:
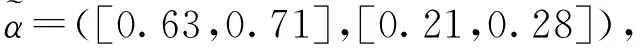
2.门诊患者满意度评价以门诊维度为例,将医院A1各属性区间直觉模糊数加权集结:
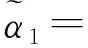
[0.210.340.220.370.100.29,0.280.340.270.370.150.29])=([0.697,0.755],[0.172,0.231]);
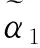
老年糖尿病肺部感染患者空腹血糖变化作为肺部感染致老年多器官功能不全综合征诊断指标的可行性研究 ……… 谭清武 徐海涛 唐静怡 等(1)7
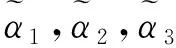
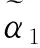
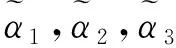
经比较C1 3.住院患者满意度评价以住院维度为例,将医院A1各属性区间直觉模糊数加权集结: [0.220.350.230.340.120.31,0.270.350.250.340.150.31])=([0.717,0.750],[0.185,0.219]); 经比较C1 [0.1720.450.1850.55,0.2310.450.2190.55])=([0.708,0.752],[0.179,0.224])。 综上,医院A3的门诊、住院、整体患者满意度均为最优,见表1。 表1 门诊、住院和整体维度下综合评价建模计算结果 Fuzzy集、直觉模糊集和区间直觉模糊集等理论提出并逐步完善,应用研究尚不深入,医药卫生管理决策问题中未见应用。传统Fuzzy集方法[6-7]仅利用单个值隶属度,后来理论界用直觉模糊数从隶属度、非隶属度和犹豫度描述模糊信息,之后又继续将隶属度、非隶属度以模糊区间数形式描述或刻画,适应决策者认知思维和模糊信息测度要求。 本文以患者满意度为例验证方法合理性、操作可行性。患者满意度评价归为多属性决策或评价研究范畴,调研设计和模型方案是信息提取及方法选用的条件。将每个属性满意度调查结果转化计算为隶属度、非隶属度区间直觉模糊数,加权集结后与理想最优、最劣值计算距离,由“逼近理想解”寻求相对贴近度。初始资料为模糊信息,经集结变为精确量值,由此从门诊、住院和整体维度对医院患者满意度综合排序。 满意度是在患者主观认识基础上提取信息,调查结果会有主观偏好性、动态变化性,以区间模糊数测度相关信息会更合理。以区间直觉模糊数、欧式距离、理想点和相对贴近度知识建立模型,分别以模糊集论、决策理论、系统工程等知识支持,流程具体、操作可行、解读明确、信息充分,不受对象及属性个数限制,excel易于编排实现。该方案可为卫生或管理领域决策工作者提供方法借鉴,并推广于综合评价应用问题研究。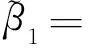
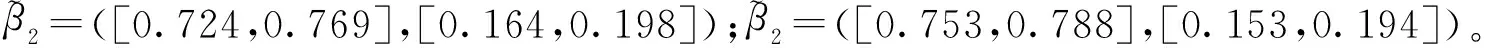

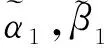
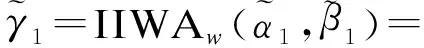
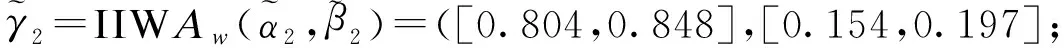
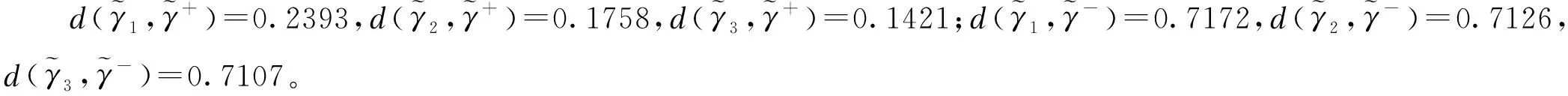

讨 论

