基于指数分布的生存资料盲态下样本量再估计方法*

朱　典　王　陵　李婵娟　蒋志伟　张　威　王治东　吴克坚　李　晨　夏结来△

【提　要】　目的　针对生存分析样本量再估计的适应性设计临床试验,本文基于指数分布,提出盲态下生存资料的样本量再估计方法。方法　采用蒙特卡洛模拟方法,预设4个期中分析时间点,以参数初始估计值M10为均数暂定搜索范围为M10±0.5M10,在该搜索范围内产生指数分布随机数对期中分析时的截尾生存数据进行填补,对填补后的数据进行极大似然估计,得到试验参数的再估计值若落在搜索范围外,则需更改搜索范围以包含并重新进行搜索直至落在搜索范围内,此时的即为试验参数的再估计值,在此参数的基础上重新估计样本量,并比较4个期中分析点的样本量再估计结果,确定1个最合适的期中分析时间点。 结果　经过期中分析调整后的样本量接近真实值,且期中分析时间点越向后移,样本量估计结果越接近真实值,变异越小。 结论　建议在入组结束并完成1/4最短随访时间时进行一次期中分析重新估计样本量,根据估计结果考虑是否增加样本量。

传统的临床试验在试验开展前,研究者根据前期研究结果并结合相关文献设定试验关键参数,对样本量进行估计,以期望达到设定的检验效能。但是,试验开始前对参数的设定可能存在较大偏差,以此为基础估计的样本量有可能不足以达到预设的检验效能。而在适应性设计中允许在试验开始之后根据已得到的部分试验数据进行期中分析,重新估计样本量,以使试验达到预设的检验效能[1]。

对于不同类型的数据,需采用不同的样本量再估计方法。对于正态资料,Gould[2]等人提出一种基于EM算法的盲态下样本量再估计方法,在期中分析时对试验数据的方差进行重新估计。对于二分类变量,Shih[3]等人提出一种基于分层理念的盲态下样本量再估计方法,在期中分析时对两组的事件发生率重新估计;Friede[4]等人提出一种基于负二项分布的盲态下样本量再估计方法,在期中分析时以负二项分布为基础建模,对总体率进行重新估计。对于生存资料,Togo[5]等人提出一种基于偏似然估计的样本量再估计方法,在期中分析时对数据揭盲,并根据构建的模型对两组之间的风险比(HR)进行重新估计;Todd[6]等人提出一种基于外推法的盲态下生存数据样本量再估计方法,假设两组之间的风险比(HR)不变,试验进展过程中在多个预设时间点上进行多次期中分析,并根据多次期中分析结果求效应的平均差别,推断试验结束时的生存率。

期中分析时对试验揭盲会导致Ⅰ型错误的膨胀,从而影响试验的完整性。而在盲态下进行期中分析,对Ⅰ型错误的影响可以忽略,无需对检验水准进行校正[1]。本研究提出的生存资料样本量再估计方法是在盲态下只进行一次期中分析,该方法以极大似然估计为基础,结合Todd[6]等人的研究方法,假定生存数据服从指数分布,两组之间的风险比(HR)不变,在期中分析时对其他试验参数进行重新估计,提出生存资料样本量再估计的新方法。

原理与方法

对于服从指数分布的生存资料,期中分析在盲态下进行,其分组未知,相当于求解混合指数分布的参数问题。EM算法是Dempster[7]等人提出一种对于不完全数据进行参数估计的方法,以极大似然估计为基础进行迭代,最终得到一个局部最优参数估计的迭代算法。朱利平[8]等人将EM算法应用到电子元件的寿命试验中。研究表明,样本的截尾比例越大,EM算法参数估计的效率越差,且估计结果往往依赖于初始值和收敛标准的设定[8-9]。在对生存资料进行期中分析时,往往产生大量的截尾数据。因此,本研究提出填补数据的方法,在期中分析时,用参数的初始估计值产生模拟数据,并用模拟数据中大于期中分析时间点的数据填补截尾数据,经过填补后的数据包含一定比例的真实参数信息和一定比例的填补参数信息。本研究结合EM算法的思想,但考虑到其参数估计结果依赖于初始值的设定,因此,提出在期中分析时以初始估计值为均值确定搜索范围(hunting zone,HZ)对实际数据进行填补,然后,对填补后的数据进行极大似然估计。若初始估计值非常接近参数真实值,则此时参数的初始估计值与极大似然估计值也非常接近,则在搜索范围内筛选出参数的极大似然估计值与初始估计值之差最小的参数极大似然估计值作为期中分析时的参数估计值。

极大似然法是混合分布参数估计的常用方法,期中分析时对服从混合指数分布的生存数据应用极大似然法,重新估计混合指数分布的参数进行样本量再估计。期中分析时的数据是含有缺失数据的观测数据,若用K表示分组(未知),X表示观测数据,则包含分组的完整数据用Y表示:Y=(X,K)。λ是指数分布的参数,f(K|X,λ)是给定观测数据X=Xi,λ=λi的条件下缺失数据K的条件密度。通过对观测数据X的对数似然函数lnL(λ|X)求极大值得到λ的极大似然估计值。期中分析时的生存时间为观测数据,用X表示,xi表示每个受试者的生存时间。受试者的分组情况用K表示,Ki=1表示受试者接受对照组治疗,Ki=0表示受试者接受试验组治疗,因对照组与试验组的样本量比例为1:1,所以Ki服从二项分布,π(Ki=1)=π(Ki=0)=0.5,但是,期中分析是在盲态下进行,因此Ki是不能被观测到的随机变量。用λc表示对照组的风险率,λt表示试验组的风险率,则对照组受试者的生存时间服从指数分布f1i,其概率密度函数为:

f1i=λce-λcxi(λc>0),

试验组受试者的生存时间服从指数分布f2i,其概率密度为:

f2i=λte-λtxi(λt>0),

则xi服从混合指数分布fi,其概率密度函数为:

fi=0.5f1i+0.5f2i.

在混合指数分布fi中,记θ=(λc,λt),则xi和Ki的联合分布为:

g(xi,Ki,θ)=(0.5f1i)Ki(0.5f2i)1-Ki,

因此,Ki在xi给定时的条件分布为:

xi给定时θ的似然函数为:

对数似然函数为:

给定参数初始估计值θ0(λc0,λt0)时,该对数似然函数的期望为:

通过极大化Q(θ,θ0)函数可得到参数θ(λc,λt)的极大似然估计值[8]。

在以事件为终点的随机对照临床试验中,研究者根据以往数据估计受试者的生存时间,进而转换为风险率λ进行样本量计算。指数分布下风险率λ与中位生存时间M的转换公式为:

本研究中定义随访时间为最后一个受试者入组开始至研究结束所经历的时间。由于入组时间不同,因此最后一个入组受试者的随访时间决定了总研究时长,且所有受试者均随访至研究结束时间点,此时样本量计算公式为(1)～(3)所示[10]:

(1)

(2)

(3)

公式(1)～(3)中,λc和λt分别是对照组和试验组的风险率,T0是入组时间,T是总研究时长,k是试验组和对照组的样本含量比例,nc是对照组样本量。

采用Monte Carlo模拟构建基于指数分布的生存资料模型,对模拟产生的生存资料进行log-rank检验,探讨本研究方法对生存资料样本量再估计的准确性和稳定性。本研究所有数据均由模拟产生,采用SAS 9.1.3统计分析软件编写程序,并进行数据分析。

1.参数设置

对于一个基于log-rank检验的双臂临床试验,对照组与试验组样本比例为1:1,生存时间服从指数分布。试验的真实参数如下,对照组的中位生存时间为M1=1年,对照组与试验组的风险比HR为0.65和0.75,试验入组时间为T0=0.5年,受试者在入组期内均匀入组,最短随访时间为t=2年,总研究时长为T=T0+t=2.5年,检验水准α为双侧0.05,检验效能1-β为0.8,则对照组的风险率λc为ln2/M1,试验组的中位生存时间为M2=M1/HR,风险率λt为ln2/M2,试验所需样本量为N。

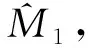
在进行期中分析的临床试验中,一般进行1～2次期中分析,本模拟研究考虑最大可能性,设定4个期中分析时间点(interim,I),并比较4个期中分析时间点的样本量再估计结果,最终选定一个合理的期中分析时间点。4个期中分析时间点分别为I1-I4,I1是入组结束时(T0),I2是完成1/4随访时间时(T0+0.25t),I3是完成1/2随访时间时(T0+0.5t),I4是完成3/4随访时间时(T0+0.75t)。

2.模拟步骤

(1)根据预先设定的参数,运用SAS随机函数ranexp(seed)先产生参数为M1、M2的指数分布数据x,受试者均匀入组,入组间隔为tn=T0/N0,入组顺序即为随机数的序号ob。令int=I-T0,令y=x-(N0-ob)×tn,将其中y>int者设定为y=int。

(2)重复步骤(1)产生参数为HM10、HM20的指数分布数据x,用其中y>int者填补参数为M1,M2数据中y=int的截尾数据,即为期中分析的数据。每个搜索范围内有多个HM10,以HZ1(0.25～0.75)为例,搜索间隔为0.1年,则有0.25、0.35、0.45、0.55、0.65、0.75共6种填补参数,根据HR求得HM20,并以HM10、HM20为参数产生6组混合指数分布随机数,用该6组随机数中y>int的数据分别填补一次截尾数据,产生6组期中分析数据。

模拟结果

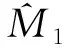
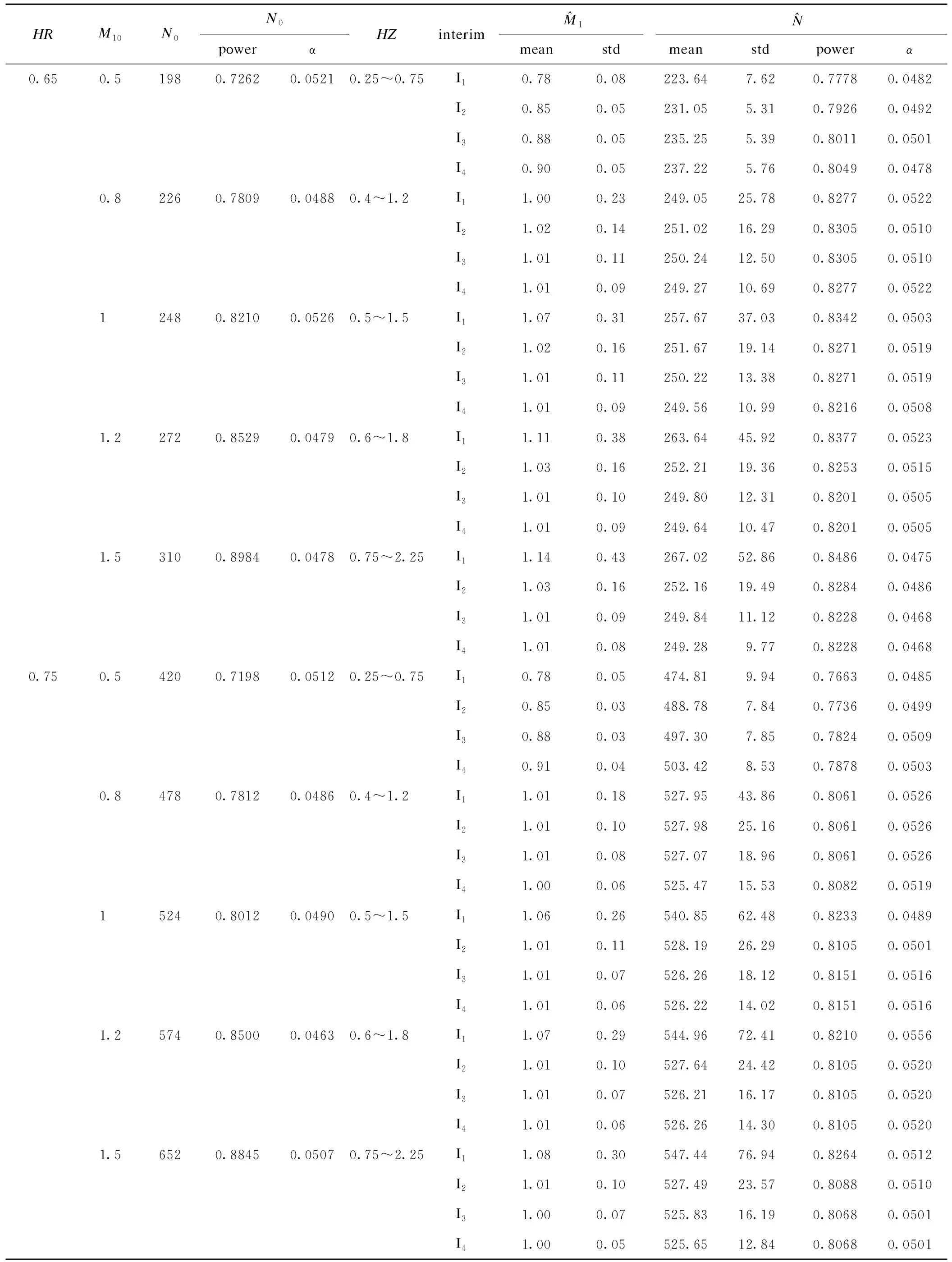
表1　不同HR时4个期中分析点不同HZ的样本量再估计结果

表2　不同HR时4个期中分析点HZ11的样本量再估计结果

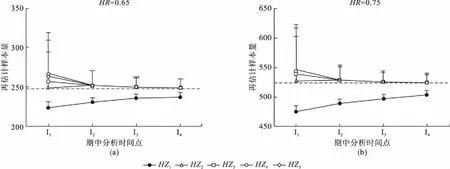
图1　不同HR时再估计样本量与期中分析时间点、HZ之间的关系

图2　不同HR时再估计样本量与期中分析时间点、HZ(包含参数真实值)之间的关系

图3　各期中分析时间点上HZ11-HZ5再估计样本量的α(a)和power(b)

模拟示例

讨　　论

药物临床试验的投入巨大,而样本量是否充足直接关系到试验的成败。若在试验设计阶段对试验参数的估计存在较大的不确定性,建议采用适应性设计,预设期中分析点对样本量进行再估计,根据估计结果考虑是否增加样本量。一般期中分析时只考虑是否增加样本量以维持把握度,而不考虑降低样本量[1]。Todd[6]等人提出的盲态下样本量再估计方法,需要设定多个期中分析时间点进行多次期中分析,具体实施有一定的难度。本研究提出的盲态下生存资料样本量再估计方法,只需要进行一次期中分析。本研究假设对照组与试验组的样本量之比为1:1,风险比为HR,α为0.05,power为0.8,并假设5个不同的M10,并以M10为均值暂定搜索范围为M10±0.5M10,比较4个期中分析点上不同搜索范围下样本量再估计结果。模拟研究表明,在期中分析点I2～I4,当搜索范围包含参数真实值时,经过期中分析调整后的样本量接近真实值,且样本量估计结果变异较小。在I1时间点时经填补的期中分析数据包含真实参数信息较少,搜索结果与填补参数相关性较大,因此样本量再估计结果呈现出与搜索范围值大小相关的现象,但在I2～ I4时间点时未出现该现象。

综上所述,并考虑到实际应用中,若样本量再估计结果大于初始样本量,需要继续追加样本量,并完成相同的随访时间t,此时期中分析时间点越晚,则研究时间就越长,研究成本也随之增加。因此,相似背景下建议在I2(完成1/4随访时间)时进行期中分析,根据参数估计结果重新确定搜索范围,以获得更加准确的样本量。若是其他差异较大的背景时,1/4随访时间作为期中分析时间点划分的参考依据,可进行适当的调整。若样本量再估计结果比试验设计之初的样本量少,则维持原定样本量不变;反之,则根据样本量再估计结果考虑增加样本量以维持把握度。本研究的不足之处是在HR恒定不变的假设下进行模拟研究,后续研究将会考虑HR改变时的情况。