水平掏土纠偏沉降计算及非线性有限元分析*

潘磊刘廷滨张家玮王作伟王伟明

（1.兰州交通大学土木工程学院 730070；2.兰州交通大学甘肃省道路桥梁与地下工程重点实验室 730070）

引言

针对倾斜建筑物，常用的纠偏方法［1］有：顶升或抬升法、阻沉法、迫降法、调整上部结构法和综合纠偏法，迫降法中有一种纠偏方法—掏土纠偏法［2-7］。通过掏土纠偏后许多的古塔及现有建筑重新达到了正常使用要求［8-10］。至今，国内外学者对掏土纠偏法做了大量的研究。1962年，意大利工程师Terracina针对比萨斜塔的倾斜恶化问题提出掏土法，并于1999年应用于比萨斜塔纠偏；殷和平等人［11］研究了某小学综合楼纠偏加固施工和监测；朱彦鹏等人［12］对湿陷性黄土地区倾斜建筑物的膨胀法纠偏加固理论分析与实践进行了研究；秦尚林等人［4］研究了水平掏土法与注浆技术在建筑物纠偏中的应用。但是，众多的研究主要集中于实践方面，并未涉及不同纠偏控制因素的沉降变化规律，以及并未把理论计算公式计算值与实际工程的沉降进行对比分析，给出修正沉降公式。

本文针对掏土孔的孔径、孔距及孔进深三种影响因素，利用ANSYS对地基土进行非线性有限元分析，探究其沉降规律；同时，将结果与理论计算解进行对比分析，对理论计算公式进行修正，为以后纠偏理论的发展及指导施工提供科学依据。

1 数值模型

湿陷性地基土模型采用SOLID95单元，尺寸采用10m×10m×6m，上表面中央8m×8m范围内施加120kPa的均布面荷载，本构模型采用D-P模型。模型边界条件［13］设置为土层水平方向固结，竖向自由；底部土层面为竖向固结，水平方向自由。材料参数取值如表1所示，各测点布置如图1所示，地基土采用映射方法划分网格，单元尺寸为0.5m×0.5m，共有4800个单元，如图2所示。

表1 材料参数Tab.1 Material parameters

图1 测点布置Fig.1 Measuring point layout

2 孔径、孔距及孔进深对纠偏的影响

掏土法纠偏是一个时时动态的过程，通过数值模拟对施工过程中的主要影响因素进行研究，对纠偏方案的制定和指导纠偏施工等具有一定的现实意义。

图2 地基土有限元模型Fig.2 Finite element model of foundation soil

掏土纠偏过程中，掏土孔的孔径、孔距及孔进深是影响纠偏效果的主要因素。掏土孔在模型中的实现，是通过扣除等体积地基土的方法来模拟，且除孔进深工况外，其余工况的掏土孔均设置为贯通整个地基。

2.1 孔径

地基土的破坏是一个渐变的塑形破坏，且会使地基产生较大的变形，通过开挖掏土孔解除部分地基土应力，从而促使地基土的应力重新分布，加快地基的塑性变形，进而达到建筑物纠偏的目的。

在地基土模型前表面中央6m范围内设置4种孔径分别为0.1m、0.15m、0.2m、0.25m，孔距及埋深均为2m，且均匀分布的掏土孔。不同孔径影响因素下的各测点沉降量如表2所示。

表2 不同孔径影响因素下的各测点沉降量Tab.2 Displacement of each measuring point under different hole size

各测点的沉降量随着掏土孔孔径的增大而增大，并且中心处测点的沉降量最大，边界中间处测点的沉降量次之，边界角点处测点的沉降量最小，如图3所示。以各测点的沉降变化值与孔径变化量的比值，作为各测点随孔径变化的斜率，以此表示各测点随孔径变化的沉降速率变化关系，如图4所示。从图4可以看出，随着孔径的增大，中心处侧点和边界中点处测点的沉降速率呈非线性增大，但是边界角点处测点的沉降速率出现了明显的拐点，并且与其他测点的沉降斜率有较大的出入，这是因为地基土应力重新分布后，在角点处产生了较为明显的应力集中现象，对沉降产生了较大的影响。掏土纠偏时产生的沉降几乎呈二次抛物线分布，如图5所示，为了防止沉降落差太大，对上部结构产生不利影响，应从沉降小的一侧逐步向靠近重心的位置依次掏土。

图3 各测点随孔径变化的沉降Fig.3 The settlement of the test points varies with the hole size

图4 各测点随孔径变化的沉降斜率Fig.4 The slope of the settlement varies with the hole size

图5 孔径变化下的各轴沉降Fig.5 The settlement of each axis under the change of hole size

2.2 孔距

在地基土模型前表面中央6m范围内设置4种孔距分别为1.2m、1.5m、2m和3m，孔径为0.15m，埋深为2m，且均匀分布的掏土孔。不同孔距影响因素下的各测点沉降量如表3所示。

随着掏土孔孔距的增大，各测点的沉降量随之减少，变化趋势与孔径增大时相反，如图6所示。但是，斜率变化却与孔径变化下的斜率有较大出入，如图7所示，从中看出角点处测点的斜率在孔距1.2m～1.5m时出现负值，这是由于掏土孔是均匀分布，随着孔距的增大掏土孔逐步向外侧移动从而导致角点处测点的沉降量有所增加。大多数测点的沉降速率存在拐角，说明孔距对沉降速率具有较大的影响，这就要求在制定纠偏方案时，必须确定好掏土孔的孔间距，使建筑物在一定的沉降速率范围内达到纠偏的目的，防止沉降速率过大，使建筑物产生二次破坏。同时，反映出掏土孔位置的重要性。图8反应的沉降规律与孔径类似，在此不再赘述。

表3 不同孔距影响因素下的各测点沉降量Tab.3 Displacement of each measuring point under different hole spacing

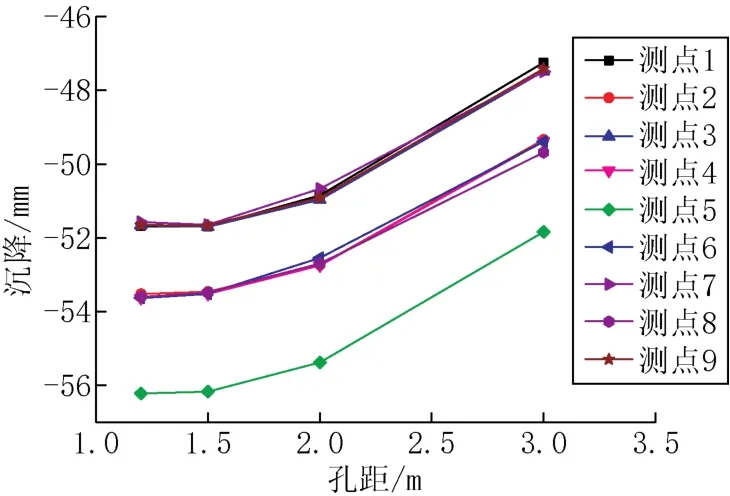
图6 各测点随孔距变化的沉降Fig.6 The settlement of the test points varies with the hole spacing

图7 各测点随孔距变化的沉降斜率Fig.7 The slope of the settlement varies with the hole spacing

图8 孔距变化下的各轴沉降Fig.8 The settlement of each axis underthe change of hole spacing

2.3 孔进深

在地基土模型前表面中央6m范围内设置3种孔进深分别为4m、6m和8m，孔径为0.15m，埋深为2m，且均匀分布的掏土孔。不同进深影响因素下的各测点沉降量，如表4所示。

表4 不同孔进深影响因素下的各测点沉降量Tab.4 Displacement of each measuring point under different hole depth

随着掏土孔进深的增大，掏土侧的沉降量明显大于掏土侧对面的沉降量，如图9所示。从图10可以看出，测点3、6、9的沉降速率为正值，说明掏土过程中掏土侧地基产生沉降而掏土侧对面一侧产生翘起现象，从而使建筑物达到掏土纠偏的目的。从图11可以看出，掏土纠偏时产生的沉降近似呈二次抛物线分布，其中，从图11b可以看出，在不同进深条件下轴A各测点的沉降较为一致，说明几乎能达到均匀回倾，掏土侧的沉降有较大出入，这就要求合理的设计施工次序。纠偏方案制定前，先用数值模拟进行分析，找出沉降变化大的位置，在沉降变化大的位置处可先设置小进深，确保实际施工过程中回倾和沉降具有较好的一致性，从而减小纠偏过程中对建筑物及基础的损伤。

3 掏土成孔后地基沉降计算

水平掏土成孔后，根据机理不同产生的变形，地基沉降可分为两部分组成：土体在压力作用下密实度增加引起的沉降ΔS1；掏土后孔侧壁土在压力作用下产生错动滑移引起的沉ΔS2。计算掏土后土层的沉降：

但是，公式（1）是在假定条件下成立，对于计算实际的沉降量，需要对该公式进行修正，修正后的公式为：

式中：β为修正系数。

图9 各测点随孔进深变化沉降Fig.9 The settlement varies with the hole depth

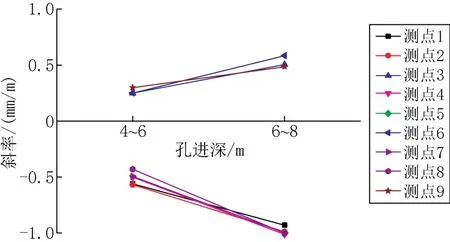
图10 各测点随孔进深变化的沉降斜率Fig.10 The slope of the settlement varies with the hole depth

图11 进深变化下的各轴沉降Fig.11 The settlement of eachaxis under the change of hole depth

3.1 计算ΔS1

由分层总和法得：

式中：e1i为第i层土压缩前的孔隙比；e2i为第i层土压缩后的孔隙比；hi为第i层土的厚度；n为土体计算分层数。

3.2 计算ΔS2

ΔS2在切向力的影响下产生错动滑移，导致掏土孔竖直方向长度变小，水平方向长度变大，形成类似椭圆形状［14］。

依据对称性特点，取半个圆拱进行受力分析，如图12所示，在A，B，O位置处铰接，掏土孔单位长度单元受侧向应力和竖向应力的影响［14］。ΔS2就是在应力作用下C点的竖向位移，简化后计算模型如图13所示。利用平衡方程得到的ΔS2表达式如式（4）所示。

图12 半圆拱受力情况Fig.12 Semi-circular arch force situation

图13 半圆拱简化结构Fig.13 Semi-circular arch simplified structure

式中：A为圆拱横截面积，A=1×t，其中t为所取圆拱厚度；R为圆拱半径；E为地基土弹性模量，，其中Es为地基土压缩模量；G为地基土剪切模量，；qV和qH为掏土孔顶部及侧部的荷载；μ为地基土泊松比；γ为地基土重度；Ka为系数，根据参考文献［4］中表3.1选取。

qV和qH取值采用文中的ANSYS非线性有限元值，代入式（3）、式（4）分别求出ΔS1、ΔS2，然后求和与非线性有限元解对比，得出式（5）中的修正参数β。

4 修正理论公式中修正系数β的确定

地基土模型的计算分层数、每层土的厚度及压缩前后孔隙比如表5所示，从而计算出地基土的沉降量。通过对比分析理论计算解与有限元分析解，得出修正理论公式中的β值。

表5 公式计算参数Tab.5 Formula calculation parameters

（1）当掏土孔孔径分别为0.1m、0.15m、0.2m和0.25m时，β取值分别为1.06、1.105、1.11和1.07。孔径不同时，β的取值变化如图14所示。

图14 不同孔径时β取值变化Fig.14 The change of β value in different hole size

孔径不同时，β的取值拟合公式如式（6）所示：

式中：d为孔径（m）。

（2）当孔距分别为1.2m、1.5m、2m和3m时，β取值分别为1.132、1.121、1.105和1.09。孔距不同时，β的取值变化如图15所示。

图15 不同孔距时β取值变化Fig.15 The change of β value in different hole spacing

孔距不同时，β的取值拟合公式如式（7）所示：

式中：l为孔距（m）。

（3）当进深分别为4m、6m和8m时，β取值分别为1.087、1.093和1.11。随进深不同，β的取值变化如图16所示。

进深不同时，β的取值拟合公式如式（8）所示：

式中：b为孔进深（m）。

图16 不同进深时取值变化Fig.16 The change of value in different hole depth

5 理论公式验证

案例［4］为一座6层的框架结构，呈“L”形，平面尺寸为22.5m×9.6m，采用天然地基，基础型式为400mm厚整板基础。根据地质勘察资料，土层自上而下依次为：①杂填土：层厚为2.0m～2.7m，fk=70kPa，Es=3.0MPa；②淤泥质粉土：层厚为4.0m～4.4m，fk=53kPa，Es=2.85MPa；③砂岩：层厚为2.0m～7.10m，fk=320kPa，Es=19.2MPa。建筑物东西两侧土层分布很不均匀，东侧淤泥质粉土层厚度很小，而西侧淤泥质粉土层较厚。

文献［4］中的工程案例，其掏土孔径为0.10m，孔距为2m，孔进深4m。利用式（6）～式（8）可以得到此时的β最大取值为1.0595，得其沉降公式计算值如表6所示。从表6可以得出，除个别测点的沉降量与公式计算值的误差稍微超过10%，其他所有测点的误差基本在10%以内且公式计算值要比实际沉降量稍大。

表6 各观测点沉降Tab.6 Settlement of observation points

6 结论

1.通过对给出的沉降计算公式引入修正系数，给出了掏土法修正沉降计算公式；

2.通过公式计算与非线性有限元分析的对比，得到孔径、孔距及孔进深不同的修正参数的取值拟合公式；

3.通过工程案例证明，本文中的修正沉降公式与实测沉降量具有较好的吻合性，且能够保证建筑物纠偏的安全性。