基于等效高斯白噪声的压制式干扰样式评价方法*

陈永森，顾　兵，杨　坡

(中国船舶重工集团公司723研究所，江苏 扬州 225001)

0　引言

压制式干扰主要用于压制雷达作用距离，降低其检测性能。由于雷达、干扰种类多样，干扰作战对象和作战任务不同，导致出现多种干扰样式的评价方法和干扰效果的评估方法、准则和指标[1]，难以形成统一的标准。

目前，对压制式干扰样式的评价大多从干扰信号本身的时域和频域特性入手[2-4]，将雷达接收机视为对压制干扰的带通滤波[4-5]，在分析对雷达的压制距离时，认为干扰机的输出功率即为干扰雷达检测的干扰功率[4-6]，忽略了作为最佳检测器的雷达匹配滤波器对干扰机输出功率的抑制，而该部分因素往往是导致干扰无法达到预期压制效果的主要因素之一。

本文依据雷达接收机的检测结构模型，分析了压制式干扰对雷达接收机判决门限的影响，提出了基于等效高斯白噪声的干扰样式评价方法，并进行了仿真验证。

1　雷达检测器模型

雷达检测器按照信号最佳检测判决进行设计，信号模型为[7]：

(1)

式中，x(t)为接收信号，n(t)为均值是零、功率谱密度为N0/2的高斯白噪声，s(t)为已知信号。在假设H0、H1下的似然函数分别为p(x|H0)、p(x|H1)，则检测判决式为：

(2)

若判决门限为VT，则对应的检测概率和虚警概率分别为：

(3)

若噪声背景为高斯白噪声，则似然比的对数[7]为：

(4)

式中，E为信号能量。根据式(4)，整理得最终信号检测的判决式：

(5)

雷达检测器依据式(5)设计检测系统结构，即由接收信号x(t)和已知信号s(t)经相关运算得到，在高斯白噪声情况下，相关等效于匹配滤波。雷达接收机在对输入信号进行滤波放大之后，均通过匹配滤波抑制噪声后进行目标信号的检测。

2　压制干扰效果评估

2.1　对雷达检测性能的影响分析

雷达检测器的判决门限决定了雷达的作用距离，当压制式干扰施加于雷达接收机时，为保证虚警概率，雷达必须提高判决门限，导致作用距离下降，因此对雷达压制距离的压制可由检测器判决门限的抬高获得。

由式(2)、式(5)知，信号能量E一定时，判决门限除了与干扰功率谱密度有关之外，还与干扰的分布特性pj(x)相关。由于压制干扰样式的种类较多、分布特性多样，对雷达接收机检测概率的影响各不相同，难以采用统一的手段进行评估。若从雷达信号检测的角度，将不同种类的干扰等效为一定功率的高斯白噪声，二者对雷达接收机判决门限的影响一致，说明对雷达作用距离的压制效果也一致，因此可以利用该等效高斯白噪声的功率值对不同干扰样式的压制效果进行对比、分析和评价。

2.2　模型的建立

假设干扰经过雷达接收机匹配滤波之后，其概率分布为pj(x)，则由式(2)得：

= -Kjs+Kj

(6)

若功率为σj0的高斯白噪声和干扰对判决门限的影响一致，则有：

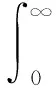
(7)

式中，p0(x)为高斯概率密度函数，所以：

(8)

即为等效的高斯白噪声的功率谱密度表达式。

由式(5)，雷达判决门限变为：

VT=((σj0+N0)/2)ln(λ)+E/2

(9)

式中，N0、λ、E为雷达自身参数，仅σj0与干扰相关。

2.3　压制干扰效果的评估

由式(9)知，在压制干扰的作用下，雷达的判决门限抬高了σj0ln(λ)/2，σj0越大，门限抬高越多，压制效果越好，否则压制效果越差，因而可用σj0评估对雷达的压制效果。

不同干扰样式均可由式(8)计算等效的σj0，进而获得压制后的雷达的判决门限，不受干扰样式的种类和分布特性的影响。

由式(5)、式(8)、式(9)可知，判决门限还与已知信号s(t)有关，由于s(t)为雷达辐射信号，因此对不同的雷达辐射信号，其等效的高斯噪声功率σj0不同，在分析时需要根据雷达辐射信号分析对应的等效高斯白噪声的功率。

压制式干扰的设计和使用应以提高其等效的高斯白噪声功率为目的，实现对雷达检测门限的抬高和作用距离的压制。

此外，定义系数：

η=σj0/Pj

(10)

式中，η表示压制式干扰的效率。η的物理意义在于表明通过雷达匹配滤波后的干扰剩余占总的干扰功率的比例。η数值越大，干扰的效率越高。

3　仿真验证

下面对以上分析进行仿真，参数如下：雷达目标回波信号幅度0.5 V，时宽5 μs，中心频率1 MHz，雷达接收机带宽20 MHz；压制干扰为噪声调幅干扰，瞄频误差Δf=0.75B，B为雷达信号带宽，幅度调制带宽为3B。雷达目标回波和干扰信号的时域波形如图1(a)所示，经雷达接收机匹配滤波后，干扰功率被抑制，但存在一定的剩余，时域波形如图1(b)所示。干扰在匹配滤波前后的功率谱密度如图2所示。可以看出，原始干扰信号的功率由载波和边带两部分构成，但功率主要集中在载波频率附近。经匹配滤波器后，其功率谱受匹配滤波器幅频响应的调制出现变化，表现在载波功率下降，部分边带功率被抑制。

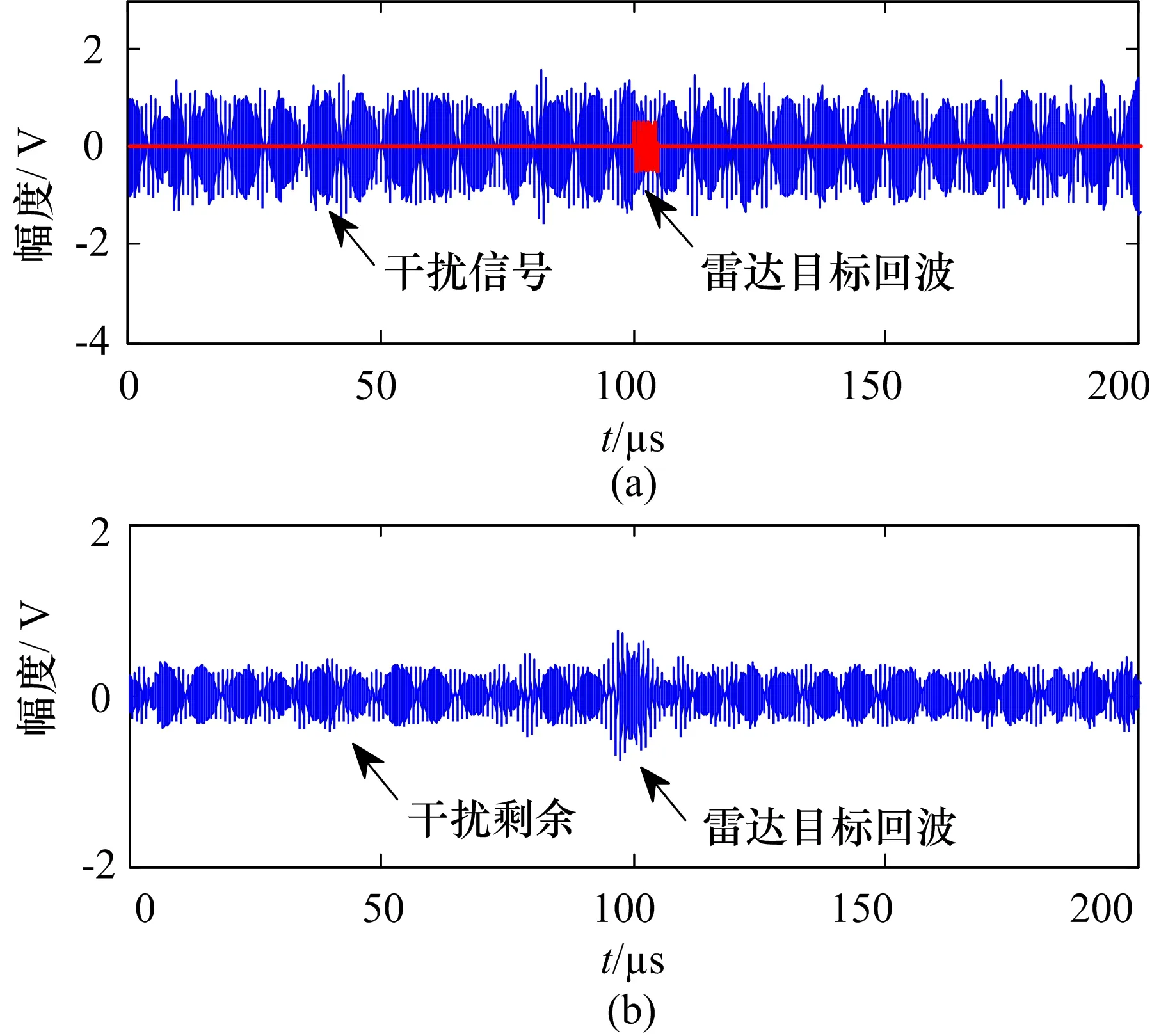
图1　干扰和信号时域波形图

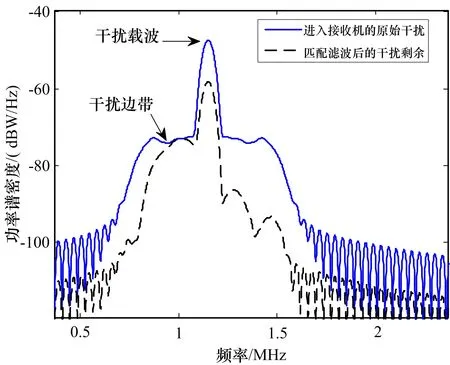
图2　匹配滤波前后干扰功率谱密度

统计匹配滤波后的幅度分布特性如图3所示。通过瑞利分布、Weibull分布和高斯分布曲线的拟合可以看出，其幅度服从高斯分布，利用式(8)计算得等效的高斯白噪声功率谱密度σj0=-63.1 dBW/Hz，折算到匹配滤波之前的功率为9.6 W。

匹配滤波器输出的功率谱特性如图4所示。对比图2可以发现， 与信号频带相重叠的干扰功率可以通过匹配滤波器，对雷达的信号检测形成干扰，特别是瞄频精度较高时，干扰载波功率通过匹配滤波器，形成较大的干扰；而高斯噪声干扰的功率谱为定值，经匹配滤波，仅与信号频带一致的部分功率未被抑制，对雷达信号检测形成干扰。

图3　匹配滤波后的幅度分布特性统计

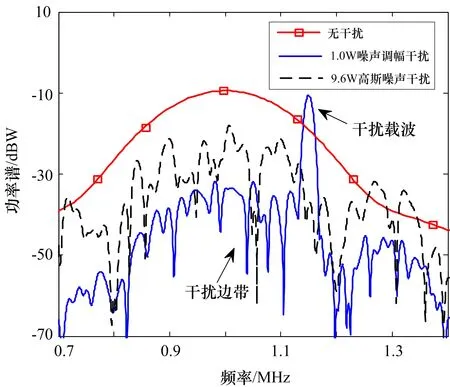
图4　匹配滤波器输出的功率谱

两种干扰在匹配滤波前后的功率、检测概率以及信干比的仿真结果如表1所示，可以发现二者基本保持一致，因此对雷达信号检测的影响也基本一致。表1中同时给出了9.6 W的高斯白噪声通过匹配滤波器的理论计算结果和仿真结果抑制，可以说明仿真的有效性。

表1同时给出了两种干扰的干扰效率，对比可以发现，两种干扰的干扰效率均不高，瞄频精度为0.75B时，噪声调幅的干扰效率是高斯白噪声干扰的10倍。当瞄频精度变化时对应的压制干扰效率η仿真结果如图5所示。可以看出，噪声调幅干扰的干扰效率受瞄频误差影响较大。当瞄频精度高于0.5倍的信号带宽时，可实现较高的干扰效率。随着瞄频误差的增加，干扰效率迅速下降，当瞄频精度超过1B时，干扰通过匹配滤波器的副瓣进入雷达接收机，导致干扰效率出现波动。而高斯噪声干扰的η不受瞄频误差的限制，但是效率较低。通过仿真，实现了两种干扰对比的量化分析。

表1　仿真和理论计算对比

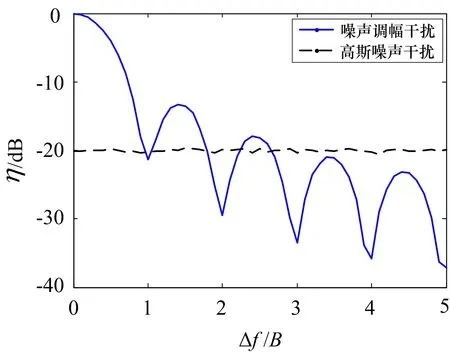
图5　不同瞄频误差时的干扰效率仿真结果

以上仿真说明:

1)通过将不同的干扰样式等效为一定的高斯白噪声功率，可以对不同干扰样式的压制效果进行对比，指导干扰样式的设计、分析和评价。

2)干扰样式的压制效果除了与自身的参数相关外，还和雷达的信号波形以及瞄频精度密切关联。

该仿真结论和分析结果保持一致。

4　结束语

压制式干扰效果的评估是干扰机干扰能力和雷达

抗干扰能力不可或缺的要求， 本文从雷达最佳检测器的角度，理论分析了干扰对雷达检测性能的影响，结果表明压制效果由雷达检测器的干扰剩余功率和其分布特性决定，提出了采用等效高斯白噪声的干扰效果评估方法，可对不同干扰样式的干扰效果进行对比分析，指导干扰样式的设计和选择。■