一类旋转对称bent函数的构造
郑 东,严宏超,赵庆兰
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
布尔函数在密码学[1]中具有广泛应用[2-5],可以作为流密码的非线性组件[4]以及分组密码的S-盒[6]中的核心组件。
bent函数[7]是Walsh谱取值为±2n/2的一类布尔函数,与仿射函数集合具有最大汉明距离,能够有效抵抗线性攻击和最佳仿射逼近攻击。旋转对称(rotation symmetric boolean functions,RotS)布尔函数[5]也称为幂等函数[8],当输入向量循环左移时其输出值保持不变。利用RotS布尔函数可实现Message Digest系列中的杂凑压缩算法,还可进行快速Walsh变换[9]。
当变元数n=2m,且m/gcd (m,t)是奇数时(1≤t≤m-1),可构造出一类二次和三次旋转对称bent函数ft(x)[4,10]。代数次数从2到m的2m元旋转对称bent函数的构造[11],首次将旋转对称bent函数的代数次数提高至大于3。通过修改代数次数较低的旋转对称bent函数,也可得到两类代数次数为d(3≤d≤m)的旋转对称bent函数[12]。
本文将在文献[4,12]的基础上,深究旋转对称bent函数的性质和构造,给出一个Maiorana-McFarland类[13]函数,并证明该函数为旋转对称bent函数。当变元数n=2m(m∈+)为偶数时,所给新函数的代数次数可达m。
1 基础知识
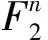
任一n元布尔函数f均可以用其代数正规型(algebraic normal form,ANF)唯一表示为
(1)
其中,向量
α=(α0,α1,…,αn-1),x=(x0,x1,…,xn-1),
的系数取值。
定义向量x的支撑集为
supp(x)={i:xi=1}。
其中所含元素“1”的个数称为向量x的汉明重量,记为w(x)。布尔函数f(x)的支撑集定义为
其中所含元素“1”的个数称为函数f(x)的汉明重量,记为w(f)。任意的两个布尔函数f(x)和g(x)的汉明距离满足
dH(f,g)=w(f+g)。
如果布尔函数的f(x)汉明重量w(f)=2n-1,则称该布尔函数是平衡的。
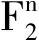
(2)
布尔函数f(x)的代数次数是其代数正规型中系数非零的单项式的最大变元个数,记为
当布尔函数f(x)的代数次数deg(f)≤1时,该函数被称为仿射函数,所有n元仿射函数的集合记为An。如果仿射函数的常数项为0,则被称其为线性函数。如果f(x)∉An,则称其为非线性函数。
布尔函数与仿射函数的相关联程度一般用非线性度(nonlinearity,NL)来描述,非线性度值的大小决定着布尔函数抵抗仿射逼近攻击的能力。非线性度是任意布尔函数f(x)和仿射函数l(x)之间的最小的汉明距离,定义为
由Parseval恒等式可知,当|Wf(α)|=2n/2时,|Wf(α)|取最小值。一般而言,对任意布尔函数f(x)都成立
NL(f)≤2n-1-2n/2。
如果某布尔函数的非线性度达到上界值,则称其为bent函数。
定义1对任意布尔函数f(x)∈Bn,其Walsh谱值满足
当且仅当f(x)是bent函数。
bent函数的变量个数只能为偶数。bent函数虽不是平衡函数,但其在布尔函数中非线性度最高。
定义2当n=2m(m∈+)时,变量和满足
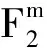
f(x,y)=π(x)y+h(x)
(3)
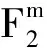
定义3任给xi∈F2(i=0,1,…,n-1),正整数k满足0≤k≤n-1,定义
(4)
其中
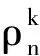
同理,也可将其扩展到多项式上,定义
其中0≤xi0<… 定义4设f(x)∈Bn,若对任意输入 都成立 则称f(x)为旋转对称布尔函数。 对RotS布尔函数而言,如果存在代表元,那么包含该代表元的轨道中,所有序列都存在于该函数的ANF中。 示例1当n=4时,给定轨道 {x0x1x2,x1x2x3,x2x3x0,x3x0x1}, 那么,该轨道的代表元是x0x1x2。 以下在m/gcd(m,t)是奇数(1≤t≤m-1)的情况下,给出一类旋转对称bent函数的构造方案,据此所构造函数的代数次数为d(3≤d≤m),可达到bent函数的最高代数次数。 引理1[12]设n=2m,f(x)∈Bn,且 (1) 对任意下标i(0≤i≤m-1),f(x)满足 f(x0,…,xi,…,xi+m,…,xn-1)= (2) 对任意下标i(0≤i≤m-1),单项式xixi+m不在f(x)的项中。 (3)f(x)是一个旋转对称布尔函数。 那么,存在一个旋转对称布尔函数 使得f(x)和γ(y)满足 f(x0,x1,…,xn-1)= 由引理1的条件(3)可知,f(x)是一个旋转对称布尔函数,故γ(y)也是一个旋转对称布尔函数。 引理2[10]令m和t是任意正整数,且 1≤t≤m-1,r=m/gcd(m,t)。 对任意满足0≤k≤gcd(m,t)的正整数k,记 xk+m-t mod m=xk+(r-1)t mod m, 且r,m和t满足 (m-t)≡(r-1)tmodm。 φ(k)(xk,xk+t,…,xk+(r-1)t)= (5) 引理3[12]令n=2m,t(1≤t≤m-1)为正整数,且xi∈F2(i=0,1,2,…,n-1),则 (6) 如果无特别说明,所涉及函数ANF的变量xj的值为jmodn。 定理1令n=2m,且t(1≤t≤m-1)是正整数,m/gcd(m,t)是奇数,布尔函数 则函数 (7) 是bent函数。若γ(y)=γ(y0,y1,…,ym-1)是代数次数为d(3≤d≤m)的旋转对称布尔函数,那么,函数f(x)是代数次数为d的旋转对称bent函数。 (8) 其中 因m/gcd(m,t)是奇数,故由引理2可知 (π0(a),π1(a),…,πm-2(a),πm-1(a)) 当0≤i≤m-1时,对f0(a,y)中的变量a和y分别进行仿射变换 yi=xi+m,ai=xi+xi+m, 可得bent函数 (9) 其中 于是 也是bent函数。 另由引理1可知γ(y)是旋转对称的,故函数f(x)也是旋转对称的。进而,当n=2m为偶数时,若γ(y)的代数次数为d(3≤d≤m),那么函数f(x)就是代数次数为d的旋转对称bent函数。 在变元数n=2m为偶数,且m/gcd(m,t)为奇数的情况下,构造出一类旋转对称bent函数,该函数具有任意的代数次数d(3≤d≤m),且该代数次数的取值可以达到目前已知的旋转对称bent函数的最优值,同时证明了该类函数是Maiorana-McFarland类bent函数。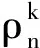
2 旋转对称bent函数的构造
f(x,…,xi+m,…,xi,…,xn-1)。
γ(x0+xm,x1+xm+1,…,xm-1+x2m-1)。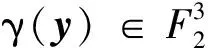
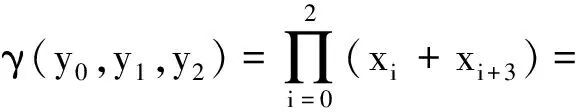
(xkxk+m-t+xk+t+xk,xk+txk+xk+2t+xk+t,…,xk+(r-1)txk+(r-2)t+xk+xk+(r-1)t),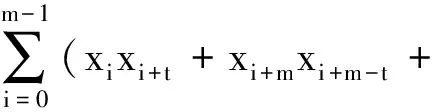
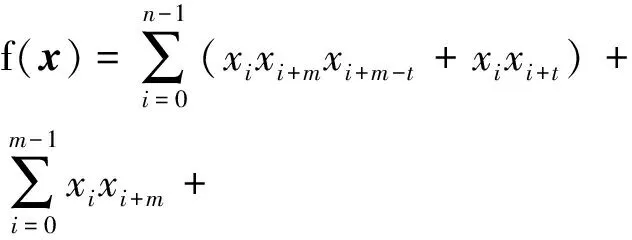

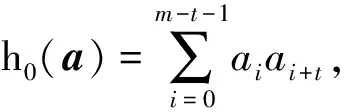
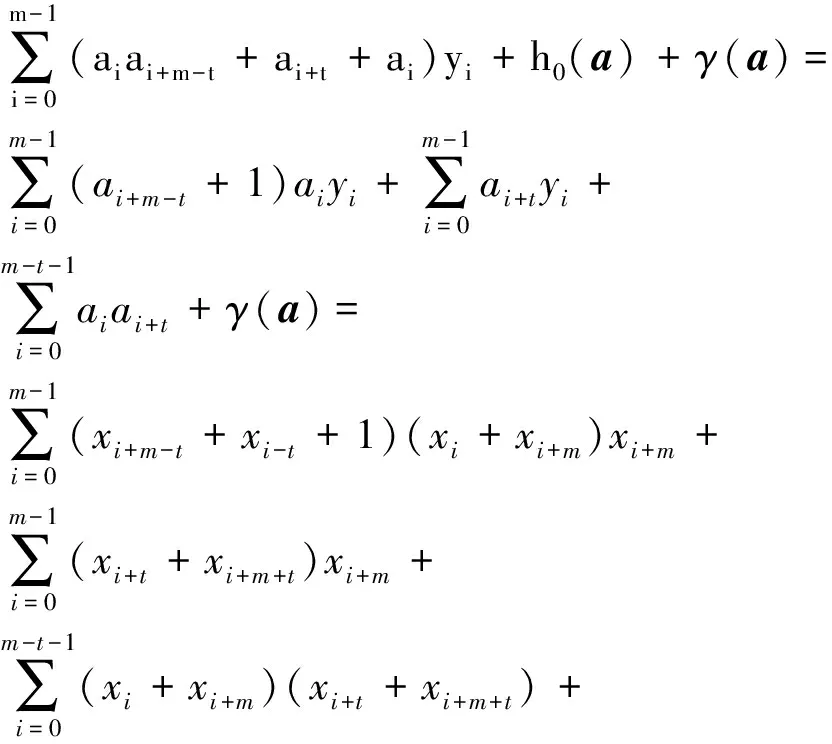
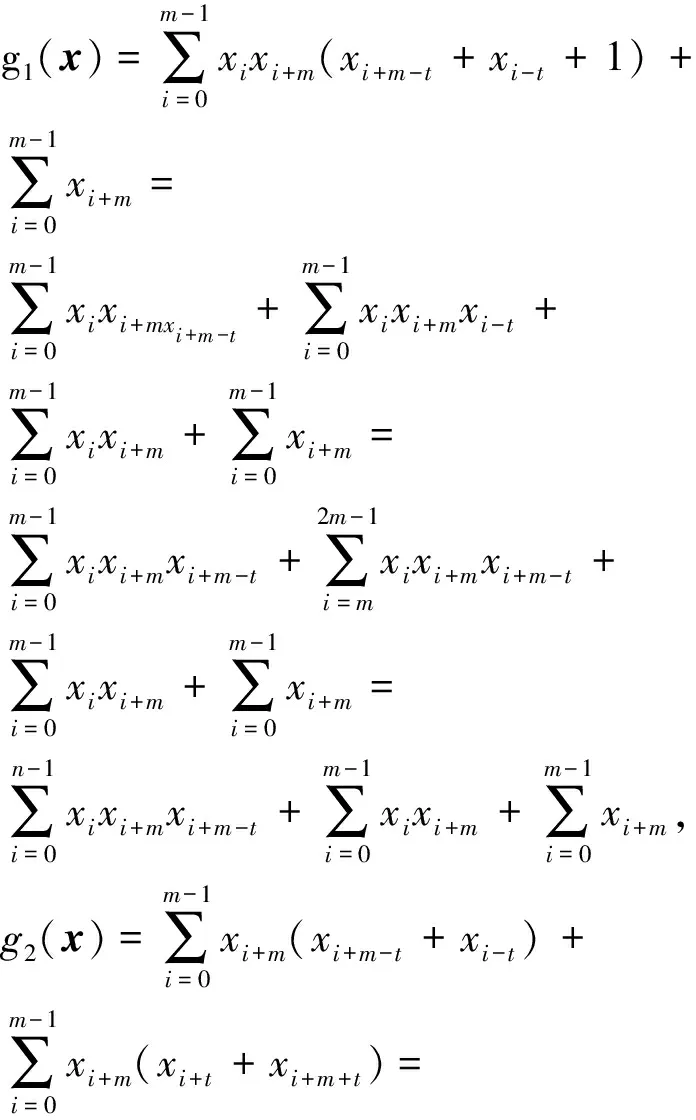
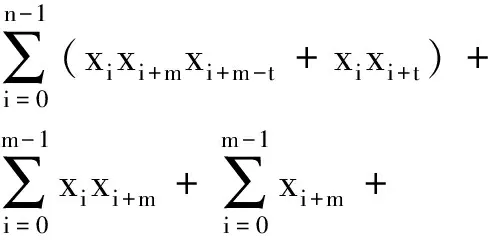
3 结语

