基于扩展序列运算的含不确定性需求响应电力系统优化调度

徐　箭, 曹慧秋, 唐程辉, 魏聪颖, 江海燕, 廖思阳

(武汉大学电气工程学院, 湖北省武汉市 430072)

0　引言

当前全球大力发展可再生能源[1],但其不确定性(随机性)和波动性的特点使得大规模并网面临巨大挑战。到2016年底,中国可再生能源累计装机容量达到570 GW[2],但弃风、弃光率居高不下[3],究其原因还是系统灵活性不足,使得可再生能源的发展受到了限制[4]。需求响应(demand response,DR)资源作为一种灵活性资源参与电力系统的调峰调频和备用,通常被认为是储能设备的低成本替代,挖掘需求响应潜力,通过需求响应来适应风电大规模接入系统,将成为未来智能电网的发展趋势[5-7]。

文献[8]设计了一种多时间尺度滚动协调的需求响应调度策略,文献[9]以最大消纳风电和系统运行成本最小为目标,建立了源荷协调多目标优化模型,文献[10-11]建立了计及大规模风电和需求响应参与的电力系统随机调度模型,这些调度模型主要是基于确定性需求响应模型来解决风电出力的不确定性,然而在需求响应过程中,由于模型参数、外部条件预测的误差以及决策主体的认知偏差,用户侧的需求响应存在不确定性。目前,针对需求响应不确定性进行分析和建模的研究较少[12-16]。

文献[12]将需求响应不确定性产生的原因归结为模型和预测的不确定性。文献[13]建立了价格型负荷随机响应模型,将价格型负荷响应不确定量视做随机注入变量,引入到源荷互动概率潮流模型中。文献[14]人为设置了需求响应不确定的范围,对该范围内的不确定响应进行备用。文献[15-16]分析了影响价格型需求响应不确定性的因素,建立了价格型负荷模糊响应模型,在此基础上对电力系统进行调度。文献[17]研究了激励型需求响应和价格型需求响应,分别建立其不确定响应下的调度成本模型。上述文献为需求响应不确定性分析提供了良好的理论依据,但研究侧重于对需求响应不确定性产生的机理和影响因素的建模,分析影响因素与需求响应不确定性的关系,未充分反映需求响应不确定性大小对电力系统调度结果的影响。

此外,综合考虑需求响应偏差和风电预测误差可以给电力系统的调度提供更加全面的信息,提高电力系统运行的经济性与稳定性,然而目前这方面的研究比较缺乏,且同时考虑需求响应和风电随机性使得该调度问题成为一个多随机变量优化问题,此类问题多采用蒙特卡洛法,存在运算量较大、计算精度难以保证等缺点[18-19]。序列运算理论只需离散采样点的信息就可实现变量的序列化描述,对系统不确定性分析时随机变量服从的分布条件要求相对较低[20-21]。将序列运算引入到需求响应的不确定性建模中不仅能够用概率性序列简洁地刻画不确定量,还可以与风电出力的概率性序列进行运算，求解多个随机变量组合运算后的新的概率分布,从而直接计算满足备用约束的概率。通过对序列的离散化处理,巧妙实现了计算中状态快速归并,在保证计算精度的条件下极大地提高了计算速度[21]。

综上所述,本文以应对风电波动性和随机性为背景,基于扩展概率性序列运算理论,建立了表征风电和需求响应不确定性的电力系统调度模型,本文提出的调度方法旨在充分反映不确定性需求响应接入电网给系统带来的成本变化与实际运行风险水平,为电力系统的调度提供参考。

1　不确定性建模

1.1　激励型负荷响应不确定性建模

激励型负荷响应指用户与电力公司签订合同,用户接受调度部门的信号对负荷进行削减,电力公司对用户削减的负荷进行补偿的响应方式。当用户的响应偏差超过一定范围时会对其进行惩罚,因而用户不响应情况较少。然而,由于响应过程中的外部环境的不确定性、信息延时和决策主体的认识偏差,用户对负荷削减信号的响应存在偏差,表现为欠响应或过响应,对调度部门下达指令后用户的响应情况进行分析具有重要意义。

激励型负荷响应的不确定性一般按照以下策略统计得来:①根据给定的基线负荷计算方法得到母线的基线负荷(假设一条母线上接一个配电网,该配电网内的负荷已经被聚合在一起);②将基线负荷减去实时量测到的负荷量即得到负荷削减量;③统计需求响应指令下的负荷削减量,即得到该需求响应调度水平下的负荷削减量的实际分布情况。然而基线负荷的计算本身存在误差,实际负荷削减量的计算并不准确,不利于统计。

因此,本文引入扩展序列运算理论对需求响应不确定性进行建模[18]。需求响应参与下的电力需求等于基线负荷和负荷削减量的差值,由于预测问题的超前性,把基线负荷、激励型负荷响应量与电力需求都看做不确定量,引入这3个量的概率分布函数,采用抽样离散化的方法,运用序列运算理论,建立求解概率分布函数参数的关键模型,得到激励型负荷响应的概率分布,具体方法如下。

1)可以认为电力需求、基线负荷和负荷削减量的实际值服从期望值为μk、方差为σk的正态分布,则其概率密度函数同式(1)第3行所示,变量的取值范围为(-∞,∞)。

2)基线负荷、激励型负荷响应量与电力需求的概率分布函数的均值为预测值,通过统计实时监测下的负荷数据,得到电力需求(需求响应参与下)的预测误差,一般在负荷预测值的3%～5%之间,则实际电力需求分布函数的方差σ0已知。

3)基线负荷和负荷削减量概率分布函数的方差用σ1和σ2表示,对含未知参数σ1和σ2的基线负荷、激励型负荷响应量的概率分布函数直接以“1”为间隔对其进行抽样序列化,得到相应的扩展概率性序列,将它们进行卷差之后采用最小二乘的处理方法逼近电力需求的扩展概率性序列,模型如式(1)所示,解模型得到σ1和σ2,从而可以得到用户响应偏差的概率分布函数。

(1)

式中:Np和Nn分别为特定预测值下实时监测得到的电力需求的概率性序列的正向长度和负向长度;x(i)为基线负荷和负荷削减量的概率性序列卷差得到的序列;a0(i)为电力需求的概率性序列;a1(i)和a2(i)分别为基线负荷和负荷削减量的概率性序列；ak(i)通过对相应的概率分布函数离散化得到;运算符号“⊖”表示序列相减;μ0,μ1,μ2分别为电力需求、基线负荷和负荷削减量的期望值。激励型负荷响应的不确定性与负荷削减量密切相关,因此本文将负荷削减量分为不同的等级,对其响应不确定性进行统计。

激励型负荷的响应成本CI为削减负荷前后的电力公司收入变化量,为负荷削减量的二次函数[17]，具体如下：

(2)

式中:qI,n,t为激励型负荷n在t时刻的负荷削减量;aI,n,t和bI,n,t分别为激励型负荷响应成本的二次项系数和一次项系数,参数的具体获取方式见附录A。

然而负荷响应过程存在不确定性,当用户欠响应时,电力公司按照实际负荷削减量进行补偿;当用户过响应时,电力公司按照下达的负荷削减量进行补偿,补偿方式如式(2)所示。另一方面,当用户欠响应时,电力公司需要承担重新购买高价发电容量来维护系统稳定性的责任,由此产生的费用称为高估代价。考虑到负荷过响应的情况,需要预留一定的向下备用,产生的费用称为低估代价。考虑负荷削减不确定激励型负荷响应成本为[22]:

CI,n,t′=

(3)

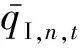
1.2　价格型负荷响应不确定性建模

价格型负荷响应是指用户根据电价调整自己的用电量,价格型负荷响应的不确定性主要是因为价格需求曲线的不确定性。价格型负荷响应的不确定性不仅跟弹性系数有关,还和电价激励水平有关[13]。因而,需要建立不同弹性系数、不同电价激励水平下的负荷响应量概率模型,模型的建立过程如下。

1)统计各母线上的负荷实测数据,根据负荷预测水平和电价激励水平将负荷实测数据分为几组(G1,G2,…,Gn)。

2)统计各组内的负荷实测值,得到不同负荷水平、电价激励水平下的负荷响应偏差量分布。

通过以上模型得到价格型负荷响应偏差的概率分布,可近似用正态分布来拟合,价格型负荷响应的边际成本CP为负荷响应量的二次函数[17]。

(4)

式中:qP,k,t为价格型负荷k在t时刻的负荷减少量;aP,k,t,bP,k,t,cP,k,t表示负荷减少对应的电力公司成本系数,参数的具体获取方式见附录B。

对于价格型负荷的不确定响应成本,不同于激励型负荷,价格型负荷的响应成本按照用户的响应量计算,考虑不确定性的价格型负荷的响应成本为[22]:

CP,k,t′=

(5)

1.3　风电功率预测误差建模

由于统计的风电功率预测误差概率分布曲线具有偏轴特性(预测值下风电的实际分布并不对称,而正态分布是对称的,不能表示这种倾斜),因此采用通用分布来描述风电功率的概率分布[23],通用分布的概率密度函数为:

(6)

式中:形状参数α,β,γ满足α>0,β>0,-∞<γ<+∞。

通用分布的累积分布函数(cumulative distribution function,CDF)定义为:

F(x)=(1+e-α(x-γ))-β

(7)

2　考虑风电出力和需求响应不确定性的日前优化调度模型

2.1　目标函数

考虑风电出力和需求响应不确定性的日前优化调度问题的目标函数如式(8)所示。

(8)

式中:T为时段数;I为火电机组数;J为风电场数;N为激励型负荷数;K为价格型负荷数;pi,t为第i台火电机组t时刻的出力;wj,t为第j个风电场t时刻的计划出力。

式(8)中第1项CG,i,t为第i台火电机组t时刻的燃料成本;第2项CUG,i,t为第i台火电机组t时刻的启停成本;第3项CW,j,t为第j个风电场t时刻的运行成本;第4项Cun,j为第j个风电场t时刻风电功率的低估成本期望值;第5项Cov,j为第j个风电场t时刻风电功率高估成本期望值[24],各项成本对应的表达式如下:

(9)

CUG,i,t=Ki(vi,t-vi,t-1)

(10)

CW,j,t(wj,t)=djwj,t

(11)

wj,t)fj(wj,t,av)dwj,t,av

(12)

wj,t,av)fj(wj,t,av)dwj,t,av

(13)

式(8)第6项和第7项分别为激励型和价格型负荷响应成本期望值,根据前面的统计模型得到激励型和价格型负荷的响应偏差的概率分布函数分别为g(εI,n,t)和g(εP,k,t)。将概率密度函数分别代入式(3)和式(5),进行期望值运算得到最终结果见附录C。

2.2　约束条件

1)功率平衡

(14)

式中:Lt为t时刻的系统总负荷预测值。

2)发电机组约束

包括出力上下限约束、最小启停时间约束和爬坡约束[24]。

3)风电出力约束

(15)

4)负荷互动量约束

(16)

(17)

5)备用约束

(18)

(19)

(20)

(21)

式中:ru,i,t和rd,i,t分别为第i台火电机组t时刻的向上和向下备用容量;qI,n,t,av和qP,k,t,av分别为第n个激励型负荷和第k个价格型负荷t时刻的实际响应量;cu和cd为对应约束条件满足的置信水平。

式(8)—式(21)构成了考虑需求响应和风电随机性的电力系统日前优化调度问题的数学模型。显然,这是一个含机会约束的混合整数非线性规划问题。

3　模型的转化与求解

3.1　机会约束的转化

上述用机会约束表示的备用约束条件在式(20)和式(21)中,激励型负荷和价格型负荷实际响应值可以写成均值和偏差值之和,风电功率的实际值也可以写成预测值和预测误差之和,则式(20)和式(21)转化为:

(22)

(23)

式中:wj,t,re为风电场j在t时刻的预测功率；εW,j,t为风电场j在t时刻的预测误差。

采用第1节方法获得系统各变量误差的概率分布后,对各变量误差分布进行扩展序列化,通过序列运算可以获得系统总体误差(备用约束右边整体)的概率分布,对系统总体误差分布进行逆序列化得到系统总体误差的概率分布和累积分布,已知系统总体误差的累积分布可以对含机会约束形式的备用约束条件进行转化,方法具体如下。

(24)

式中:运行符号“⊕”表示序列相加。

根据扩展概率性序列的含义,系统总体误差的概率分布为:

(25)

(26)

(27)

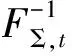
3.2　目标函数的转换

本节先不考虑风电出力和需求响应的不确定性,此时目标函数变为:

(28)

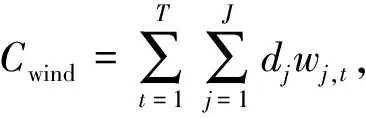
3.3　求解流程

通过对目标函数和约束条件的转换,该问题转化为一个混合整数线性规划(MILP)问题,可以采用MATLAB中的CPLEX求解器进行求解。将求解出来的机组启停状态和出力点作为内点法的初始迭代点,基于初始迭代点,进一步考虑风电和负荷响应的随机性,目标函数如式(8)所示,将目标函数线性化(详见附录E),采用内点法进行求解,从而得到考虑需求响应和风电随机性的电力系统优化调度的最优解。

基于上述分析,建立图1所示的考虑风电出力和需求响应不确定性的电力系统的优化调度问题求解思路框架。

4　算例分析

将本文所提出的模型在修改后的IEEE 30节点和修改后的IEEE 118节点系统上进行测试来验证调度模型的有效性。本文在IEEE 30节点上分析了需求响应不确定性对电力系统调度的影响,为了进一步验证考虑需求响应不确定性对调度成本和序列运算描述不确定量的有效性,在IEEE 118节点系统上进行了仿真。

图1　考虑风电和需求响应不确定性的调度问题求解思路框架Fig.1　Solving framework of optimization scheduling model considering uncertainties of wind power and demand response

4.1　IEEE 30节点系统算例

修改后的IEEE 30节点系统的网络拓扑如附录D图D2所示,系统包括6台常规机组,常规机组的总装机容量为510 MW[24],在节点6和22接入风电机组[26],风电机组总装机容量为300 MW,占总装机容量的37%,风电数据来源于蒙东某风电场,风电统计数据拟合参数见附录F表F1。在节点8和21接入激励型负荷,分别占总负荷的12%和15%,且最大可削减量均为15 MW,节点5接入价格型负荷,占总负荷的24.1%,负荷最大变化量为基线负荷的40%,负荷数据来自PJM公司[27]。备用约束的置信水平cu和cd均取0.95,高估成本系数均取为120美元/MW,低估成本系数均取为80美元/MW。调度周期为一日,时间间隔1 h。调度周期内的风电机组和负荷的预测曲线见图2(a)。

为了对比分析需求响应不确定性模型参与风电并网系统优化调度后的结果,设置了以下3种运行方式对其进行分析。

方式1:考虑风电的随机性,需求侧响应不参与调度。

方式2:考虑风电的随机性,需求侧响应参与调度,不考虑需求响应的不确定性。

方式3:同时考虑风电出力和需求响应的不确定性进行调度。

图2　不同运行方式下的调度结果Fig.2　Dispatch results in different operation modes

4.1.1随机经济调度结果分析

通过方式1和方式2对比分析需求响应对日前优化调度的影响,需求响应参与含风电电力系统的调度结果如图2(a)所示。图中左边纵坐标轴表示的是需求响应前后的系统负荷功率和风电功率,右边坐标轴表示需求响应值(正值表示负荷增加,负值表示负荷减少)。方式1和方式2发电成本、发电机启动成本、激励型负荷响应成本、价格型负荷响应成本、风电成本如表1所示。

表1　不同运行方式下日前调度成本对比Table 1　Comparison of cost in day-ahead dispatch under different operation modes

对图2(a)和表1进行分析,得到以下结论。

1)方式1,由于风电的消纳完全依赖常规机组,会使得在负荷的高峰期需要启动经济性能较差的常规机组,运行成本高。

2)方式2,在风电的高发时段,电力公司可以通过较低的电价来刺激居民用户的电量消费,消纳多余的风电出力;在用电的高峰期,通过需求响应来代替一部分价格昂贵的常规机组的出力,使得总成本减少。

由此可见,需求响应参与含风电电力系统的调度,可降低电力系统的运行成本,减少净负荷峰谷差,实现对风电波动性和反调峰性能的平抑,降低风电接入电网对电力系统的冲击。

设置方式3与方式2对比分析需求响应的不确定性对日前调度的影响,方式2和方式3下各时段激励型负荷和电价型负荷响应量如图2(b)所示,方式3各项成本仿真结果如表1所示。由表1可知,方式2和方式3调度总成本都比方式1少,考虑需求响应不确定性后,电力系统的调度成本增加了2.7%,是因为考虑柔性负荷不确定性增加了柔性负荷的调度成本,在调度时会启用出力价格更低的常规机组取代一部分柔性负荷,但对比方式1和3可知，需求响应考虑不确定性后依然能够与常规机组配合,降低系统的运行成本。

为进一步验证2种需求响应机制对调度结果的影响,设置方式4和方式5对调度结果进行分析,方式4只有激励型需求响应,方式5只有价格型需求响应(两种方式下需求响应最大响应量相同)。对比两种方式下调度成本(如表1所示)和调度结果(见附录D图D3),可以发现,激励型需求响应参与后的电力系统运行成本只是稍微降低,而价格型需求响应参与后,电力系统的运行成本有较大幅度的降低。另外,比较两种方式下负荷曲线的峰谷差可以发现,价格型需求响应比激励型需求响应的削峰填谷作用更加明显。

4.1.2电量不足期望值比较

用于表征电力系统可靠性的指标有多种,本文分析需求响应不确定性对电量不足期望值(expected energy not supplied,EENS)的影响。当风电实际出力低于调度值且系统备用供应不足时,需求响应不确定性会影响系统EENS。考虑需求响应不确定性最严重的情况,取风电出力不足时柔性负荷日欠响应期望的最大值作为柔性负荷参与电力系统调度对EENS影响的评估指标:

(29)

式中:εI,n,t<0;εP,k,t<0;R和P分别为优化结果中调用的激励型负荷和价格型负荷的集合；E(·)表示求期望值函数。

方式2和方式3的LDR-EENS分别为11.13和4.7,对比结果可以看出,考虑需求响应的不确定性对电力系统进行调度减少了电力系统的电量不足,在方式2的调度方案下,将考虑需求响应不确定性带来的风险成本计算到系统总的成本中为193 498美元,比方式3的调度成本要高,同时考虑风电和需求响应的不确定性提高了系统的可靠性,实质上降低了系统的风险成本,使得系统总体经济性得到了提升。

4.2　IEEE 118节点系统算例

IEEE 118节点系统的原始系统数据参考文献[28]。该测试系统由54个常规火电机组和186条传输线组成。该系统总火电装机容量为7 200 MW,最大负荷为6 800 MW。假设每个负载点的一天中基线负荷的变化相同。一个大型风电场接在节点65,风电总装机容量为3 000 MW。此外,风电功率预测曲线是IEEE 30节点系统中风电功率预测曲线的容量倍数的放大,需求响应负荷总量也为IEEE 30节点系统的需求响应负荷总量的相应倍数。

4.2.1需求响应不确定性对调度结果的影响

通过控制需求响应偏差分布的标准差来分析需求相应不确定性对电力公司调用需求响应量、电力公司总成本和用户收益的影响。将统计得到的需求响应偏差分布的方差作为标准1,将标准方差乘以相应的系数ΓD改变需求响应不确定性,全周期内需求响应量、电力公司总成本和用户收益结果见附录F表F2。由该表可知,需求响应不确定性越大,单位需求响应调度成本期望值越高,电力公司对需求响应的调度减少,电力公司的总成本增加,用户的期望收益也随之减少,促使用户提高响应可靠性。

4.2.2扩展序列描述不确定量的有效性

为了验证序列运算用于不确定量建模的正确性与准确性,采用均方根误差(root mean square error,RMSE)对不同方法描述价格型需求响应量和风电功率分布误差进行定量分析,定义如下:

(30)

式中:m为需求响应量和风电预测功率等级;Ng为统计分布误差分组数;xg为第g组中心位置;Fact,m(·)为实际分布的累积分布函数值;Fapp,m(·)为采用方法的累积分布函数值。

表2列出了价格型需求响应偏差RMSE和风电功率分布误差RMSE的最大值RPM和RWM及平均值RPA和RWA,并与常用考虑不确定性的方法——点估计法进行对比。

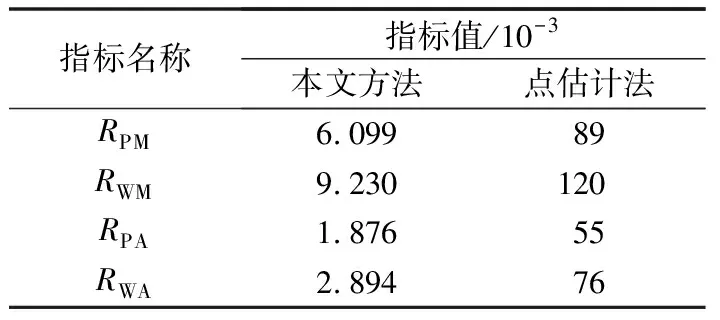
表2　两种方法的RMSE对比Table 2　Comparison of RMSE between two methods

由表2结果可知,本文采用扩展序列对各不确定量进行描述,所得到的计算结果中RMSE值均小于0.01,表明采用扩展序列对不确定量进行建模与实际值相差较小,且本文方法计算所得的RMSE值远小于点估计法的RMSE值,验证了本文采用扩展序列对不确定量建模的有效性。

在此基础上,进一步对比本文所用方法、蒙特卡洛法与点估计法的计算耗时和调度成本,结果如表3所示。蒙特卡洛法求解机会约束的方法为在每次迭代中,随机产生M个符合各变量分布特性的多元随机变量的样本,记录满足运行约束的次数为M′,根据大数定理,当M′/M的值满足置信度的要求时机会约束成立。

表3　不同方法运行结果比较Table 3　Comparison of results among different methods

由表3可知,在相同的置信度下,基于序列运算理论的方法的优化结果比蒙特卡洛法好,是因为蒙特卡洛法误差与样本容量的平方根成反比,当抽样次数没有足够大时,计算精度难以保证,为了减少计算量,蒙特卡洛法的抽样次数受到了限制(本文抽样次数取1 000)。与蒙特卡洛法相比,序列法能够更好地拟合变量的原始分布,因而优化结果更加逼近优化的最小值。基于序列运算理论的方法计算时间也更短,是因为本文采用方法耗时主要为内点法的迭代,通过序列运算理论将系统各随机变量的概率分布生成扩展概率性序列,通过卷和、卷差得到系统的总体误差概率性序列,从而可直接计算满足约束的概率。而蒙特卡洛法除了内点法的迭代,对机会约束的计算也需要耗费大量的时间,使得计算时间大大增加。

与点估计法相比,本文方法计算速度与点估计法数量级基本相当,但数值稍有增加,是因为点估计法选取风电出力和需求响应观测值作为调度值,减少了变量个数,加快了算法的收敛。值得一提的是,虽然点估计法的时间略有下降,但点估计法求得的调度成本高于序列运算法,也说明扩展序列法可以更好地考虑需求响应和风电出力的不确定性,因而其调度结果更加有效。

5　结论

1)本文所建调度模型综合考虑需求响应和风电出力的不确定性,采用机会约束的形式设置置信度水平保证系统稳定性,可辅助调度人员统筹协调系统的经济性和可靠性,具有实际应用价值。

2)考虑需求响应不确定性,提高了系统的可靠性,降低了系统的风险成本,实质上使得系统总体经济性得到了提升。

3)本文采用扩展概率性序列对电力系统的随机变量进行处理,减少了计算量,提高了运算效率,经济性也更优。

采用序列运算得到的结果与序列化步长密切相关,步长选择过大会导致运算量增大,步长选择过小无法精确描述变量,导致计算结果无法达到最优,因此为了提高本文方法的实用性,最佳步长的选择需要进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。