兼顾风险与收益的主动配电网非正常停运恢复策略

周　天, 郝丽丽, 王昊昊, 李　威,3, 李乃双

(1. 南京工业大学电气工程与控制科学学院, 江苏省南京市 211816; 2. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106; 3. 智能电网保护和控制国家重点实验室, 江苏省南京市 211106)

0　引言

配电网结构复杂、规模庞大,其故障情况也相当繁复。随着分布式电源(distributed generator,DG)的大量接入和负荷管理弹性的提升,主动配电网将获得更大的管控空间。为提高配电网的供电可靠性,现行的IEEE 1547—2003标准支持含有DG的配电网在停电事故中形成可控的计划孤岛并进行故障恢复。

当前配电网故障恢复的目标主要有结构变动最小、恢复负荷量最大、重要负荷优先恢复、恢复负荷最多、系统网损最小、系统最稳定等[1-6]。采用的求解方法则主要包括数学优化算法、启发式算法和智能优化算法等。文献[7]将孤岛划分转化为数学问题,然后利用隐枚举法求解混合整数规划问题,同时进行静态生存性约束校验并加以修正。文献[8]通过建立配电网简化模型,根据功率平衡要求以及负荷的供电可靠性要求,采取启发式的搜索方法求解孤岛划分方案。文献[9]考虑孤岛内的功率平衡约束,将负荷按权值由小到大加入生成树中,并利用Sollin算法求解最小树问题,从而实现失电区域的孤岛划分。文献[10]提出了一种改进的新型多目标进化算法对配电网故障后的恢复问题进行求解。文献[11]综合开关动作次数、停电负荷损失和网损建立故障恢复模型,并采用二进制粒子群算法搜索Pareto非支配解以获得供电恢复方案。但相关研究中,数学优化方法和智能优化方法一般不能较好地体现配电网恢复的多过程操作,而采用启发式算法则可能存在局部最优问题。

电力系统的故障恢复过程往往优先恢复重要负荷。针对负荷重要度,文献[12]按重要程度将负荷分为三级,文献[13]则将各级负荷的重要程度量化,作为不同负荷的权重。主动配电网环境下负荷控制更为灵活,然而目前负荷重要程度的粗糙划分限制了负荷的精细化管理,不利于恢复过程最大经济性的实现。配电网中DG出力和负荷需求等的随机性、设备故障和故障恢复过程中操作失效都会给恢复过程带来不确定性。文献[14]计及DG出力间歇性和负荷需求波动性,建立了基于孤岛二次停电的风险和运行风险备用的DG孤岛运行风险模型。文献[15]在确定性恢复控制模型基础上计及DG和负荷的不确定性提出鲁棒恢复优化算法,以保障配电网极端运行场景下的可靠恢复。但上述研究均没有计及恢复操作失效的风险,也没有考虑在设备异常清除之前不同的恢复策略所对应的不同过渡电网的风险差异。文献[16]用负荷从电源获得单位电量所经过的最短平均电气距离及各节点到电源所经历的最少开关设备数来反映恢复方案的运行风险度,没有考虑同类设备各自故障率的差异。

为解决上述研究存在的问题,本文引入配电网恢复操作风险、恢复过程中过渡电网风险、恢复收益和恢复代价,并将它们统一于货币量纲,建立配电网恢复综合收益优化模型。在此基础上,提出配电网非正常停运的恢复策略。

1　主动配电网恢复过程的风险评估

1.1　设备的停运风险

本文所研究的风险仅针对设备停运导致的停电风险。风险用于反映某特定环境下某种损失发生的可能性,通常表现为可能性与后果的乘积[17]:

R=pl

(1)

式中:R为事件的风险;p为事件发生概率;l为事件导致的损失。

1)设备非正常停运概率模型

电网停电事故通常源于设备的非正常停运,在配电网实际运行过程中,设备非正常停运通常由设备自身和外界因素引发[18],前者包括设备老化、绝缘损坏及设备发热等,而后者主要包括天气情况、人为影响等。综合上述因素,本文建立设备非正常停运的概率模型如下:

pa=fp(Va,Wa)

(2)

式中:pa为第a个设备的非正常停运概率;Va为第a个设备可能引发停运的自身因素;Wa为第a个设备可能引发停运的外界因素。

2)负荷重要性评价指标

GB 50613—2010标准中按照用户对供电可靠性的要求、中断供电对人身安全、经济损失造成的影响程度将负荷重要性分为三级。为了更加细致地区分停电负荷的重要程度,本文采用各负荷单位时间单位容量的恢复收益作为负荷重要性评估的量化指标:

λb=fλ(αb,βb,γb)

(3)

式中:λb为第b个负荷单位时间单位容量的停电损失;αb为第b个负荷中断供电的人身安全威胁因素;βb为第b个负荷中断供电的经济损失因素;γb为第b个负荷的供电可靠性要求。

1.2　恢复子过程的执行风险

配电网非正常停运的恢复过程通常是由多步操作顺序完成的[19]。为保证恢复策略的通用性和完善性,本文采用启发式的优化方法,通过多个恢复操作子过程的逐次优化和顺序执行实现恢复过程的整体优化,其中各子过程优化主要针对可供电电源、可恢复负荷和相应的恢复路径。

恢复路径上的设备非正常停运会引发配电网恢复子过程执行结果的不确定。本文用Rimm表示第m个子过程的执行风险,即第m个子过程执行后恢复路径上的设备非正常停运可能导致负荷恢复失效的风险,如式(4)和式(5)所示。

(4)

(5)

式中:Nm为第m个子过程恢复路径上各设备的集合;pm,n为Nm中第n个设备非正常停运的概率;lm,n为Nm中第n个设备非正常停运所造成的该子过程中负荷恢复失效带来的损失;Jm,n为Nm中第n个设备停运导致无法恢复的负荷集合;λm,n,j为Jm,n中第j个负荷单位时间内单位容量的停电损失;Pm,n,j为Jm,n中第j个负荷的负荷容量;tm,n,j为子过程执行成功所带来的负荷j的提前恢复供电时间。

本文以负荷j不采取任何恢复重构措施所需要的恢复时间Tj,r作为参考时间,结合负荷j停电至恢复供电期间各类操作(包括故障定位、隔离及恢复重构操作)所需的总体操作时间Tj,c对负荷j的提前恢复供电时间tm,n,j进行近似:

tm,n,j=Tj,r-Tj,c

(6)

式中：Tj,r可以通过历史数据和经验进行估计;Tj,c则借用文献[20]中恢复操作时间的近似方法进行量化,其表达式为

(7)

式中:Am,n,j为Nm中第n个设备停运导致无法恢复的第j个负荷恢复供电操作所需的乐观估计时间;Bm,n,j为该负荷恢复供电操作所需的悲观估计时间;Hm,n,j为该负荷恢复供电操作所需的最可能估计时间。Am,n,j,Bm,n,j和Hm,n,j均通过历史数据和经验进行估计。

求解恢复子过程的执行风险需要计算该过程中各设备非正常停运导致的恢复失效区域及相应的停电损失。针对恢复方案中各子过程网络拓扑呈现的树状结构,本文采用广度优先遍历(breadth first search,BFS)[21]从电源出发搜索正常运行的节点,求得各设备非正常停运时所对应的恢复失效区域,最后根据式(4)和式(5)分别求得各子过程中设备非正常停运导致的执行风险及恢复失效损失。

1.3　过渡电网的运行风险

每个恢复子过程结束后形成临时的过渡电网,其中包含该子过程恢复的供电区域和与该恢复区域连通的外部电网。不同的子过程将形成不同的过渡电网,不同过渡电网运行风险的差异也反映了相应恢复子过程的优劣。因此,本文将其作为优化恢复方案的风险评估指标之一,第m个子过程执行后得到的过渡电网的运行风险Rtrm定义为:

(8)

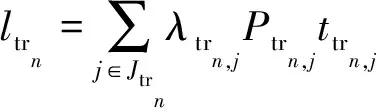
(9)

式中:Ntrm为第m个恢复子过程执行后过渡电网的所有设备集合;ptrn为Ntrm中第n个设备发生非正常停运的概率;ltrn为Ntrm中第n个设备非正常停运所造成的损失;Jtrn为Ntrm中第n个设备非正常停运导致停电的负荷集合;λtrn,j为Jtrn中第j个负荷的单位时间单位容量的停电损失;Ptrn,j为Jtrn中第j个负荷的负荷容量;ttrn,j为本次非正常停运持续的时间。

求解各个恢复子过程完成后的过渡电网运行风险,首先需要确定该过渡电网中各设备非正常停运导致的失电区域,再从失电区域的初始可供电电源出发,基于BFS快速求解相应的可供电区域,并得到该区域以外的实际失电区域。然后,根据式(8)和式(9)分别求得过渡电网运行风险和过渡电网中各设备非正常停运导致的停电损失。

1.4　恢复方案的总风险

由于恢复过程中同时存在执行风险和过渡电网运行风险,电网故障恢复的总风险定义为:

Rm=Rimm+Rtrm

(10)

式中:Rm为第m个子过程的总风险;Rimm为第m个子过程的执行风险;Rtrm为第m个子过程执行后过渡电网的运行风险。

2　非正常停运恢复策略的优化模型

在主动配电网发生非正常停运时,通常可以投入自带的DG或通过联络开关投入其他馈线的备用容量(文中简称为“联络备用”)为失电负荷转供。从改善配电网供电可靠性的角度出发,恢复过程需要考虑负荷的恢复时间、恢复容量和重要程度;从应对系统不确定性的角度出发,恢复方案的制定需计及恢复过程中的风险;从提高系统经济效益出发,恢复方案的制定应计及开关动作次数、备用电源的消耗等因素。本节将上述因素统一于经济量纲,建立了相应的配电网故障恢复策略优化模型。

2.1　负荷恢复收益

与1.2节中负荷损失模型类似,负荷恢复收益主要考虑所恢复负荷的重要程度容量及提前恢复供电时间,体现了配电网对供电可靠性的要求。第m个子过程的负荷恢复收益Im定义为:

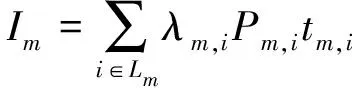
(11)

式中:Lm为第m个子过程恢复供电的负荷集合;i为负荷集合Lm中负荷的序号;λm,i为Lm中第i个负荷单位时间内单位负荷的停电损失;Pm,i为Lm中第i个负荷恢复供电的容量;tm,i为Lm中第i个负荷提前恢复供电的时间。

2.2　恢复子过程的控制代价

恢复子过程的执行伴随着购买供电电源服务[22]和开关操作等控制代价,第m个子过程的控制代价Cm定义为:

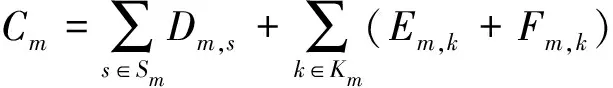
(12)

式中:Sm为第m个子过程中可供电电源的集合;s为Sm中可供电电源的序号;Dm,s为购买Sm中第s个供电电源服务的费用;Km为第m个子过程的动作开关集合;k为Km中开关的序号;Em,k为Km中第k个开关的动作折损费用;Fm,k为Km中第k个开关的操作管理费用。

2.3　恢复策略的理想优化模型

恢复方案的求解是一个多目标优化问题,应尽可能地实现整个恢复过程的负荷恢复收益最大、控制代价最小和风险最小。综上,本文提出的恢复策略优化模型为:

(13)

式中:G为配电网非正常停运恢复方案的综合收益;M为整体恢复方案所含子过程集合;m为恢复方案中恢复子过程的序号。

2.4　约束条件

1)第m个子过程的容量约束

(14)

式中:Pm,s为第m个子过程中第s个可供电电源的容量。

2)第m个子过程的电压电流约束

(15)

式中:uc,max和uc,min分别为第c个节点的电压上、下限;uc,m为第c个节点在第m个子过程中的电压值;id,max和id,min分别为第d条线路的电流上、下限;id,m为第d条线路在第m个子过程中的电流值。

3)第m个子过程的收益约束

Gm≥Gmin

(16)

式中:Gm为第m个子过程的综合恢复收益;Gmin为收益下限。

4)配电网拓扑约束

τ∈Γ

(17)

式中:τ为整体恢复方案的网络拓扑结构;Γ为网络辐射状拓扑结构的集合。

5)稳定约束

(18)

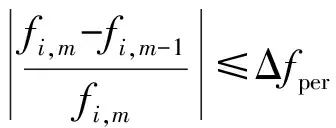
(19)

式中:ui,m为第i个节点在第m个子过程中的电压值;ui,m-1为第i个节点在第m-1个子过程中的电压值;Δuper为平均电压扰动率的允许值;fi,m为第i个节点在第m个子过程中的频率值;fi,m-1为第i个节点在第m-1个子过程中的频率值;Δfper为平均频率扰动率的允许值。

其中,式(18)为电压稳定约束;式(19)为频率稳定约束。

2.5　模拟无后效性的恢复子过程惩罚优化模型

在多过程恢复流程中,如果可投入备用电源和待恢复负荷的数量较多,各子过程不同的投入顺序会使恢复策略的解空间变得极其复杂,恢复问题将变得难以求解。因此,本文采用基于贪心策略的启发式搜索算法,将恢复控制方案的求解由多步优化的超大解空间寻优转变为单步优化的逐次寻优。

由于贪心策不是对所有问题都能得到全局最优解,因此要避免出现局部最优解,关键在于采用的贪心策略必须具备无后效性,即某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响[23]。

在本文所研究的配电网恢复问题中,由于辐射状拓扑约束要求恢复过程中形成的每个连通域上的联络备用数量不能超过一个,因此,如果当前过程投入的电源为联络备用,则所采用的启发式方法就可能会限制后续涉及其他联络备用的恢复路径搜索,从而导致最终方案不是全局最优。为减少算法对优化结果的影响,本文在优化过程中引入考虑路径搜索限制的罚函数,使采用的贪心策略近似模拟无后效性算法。该罚函数的惩罚机制为:在计算某供电电源投入带来的收益时,如果该电源为联络备用或该电源投入后形成的连通域上存在联络备用,则根据该电源恢复连通域上的待恢复负荷以及为满足辐射状拓扑约束而必须放弃的联络备用的容量对该子过程进行惩罚。罚函数的表达式如下式所示。

Mm=α∑PL+β∑PB

(20)

式中:Mm为第m个子过程的罚函数;PL为该过程恢复连通域上的待恢复负荷容量;PB为恢复连通域上为满足辐射状拓扑约束而必须放弃的联络备用容量;α和β分别为两者的等效代价系数,使罚函数的值与子过程恢复收益处于相同的单位和数量级。

由此,模拟无后效性的逐步优化恢复子过程惩罚优化模型定义为:

maxGm=Im-Cm-μRm-Mm

(21)

3　主动配电网非正常停运恢复策略

3.1　联络备用的容量等值

为确保系统结构变动最小,同时考虑到DG和联络备用不同的运行特性会使恢复方案的求解复杂化,本文将联络备用等效为具有一定容量的V/f控制的电源[24]。该方法可以有效降低复杂配电网非正常停运情况下供电恢复方案的求解难度,提高求解速度。

假设一条馈线含有的备用容量为PS,可将该馈线在联络开关处等效为输出容量在[0,PS]区间内的可控电源,其电压和频率等于外网联络开关处的电压和频率,其中PS的计算公式如下:

PS=Pv,max-Pv

(22)

式中:Pv为故障发生前联络开关所联络的第v条馈线的运行功率;Pv,max为该联络开关所联络的第v条馈线的最大功率。

3.2　配电网非正常停运后供电恢复方案求解

本文采用基于贪心策略的启发式方法对优化目标进行求解。该方法结合系统结构变动最小的恢复原则,从失电区域内的可供电电源出发,搜索并逐步恢复失电负荷,保证各过程目标收益最大且满足约束条件。本文假设配电网中的负荷均为可控,且母线节点之间均设置有分段开关。

由于在启发式恢复流程中,单一电源和负荷匹配后所形成的各个恢复区域可能出现电源容量富余,因此同时失电区域内也可能存在需要多个电源同时投入恢复供电的大容量负荷。为了确保失电区域内失电负荷最少和可供电电源容量的充分利用,应当在单一电源和负荷匹配方案的基础上,针对上述情况采取多电源协调恢复的方法,即利用多个恢复区域内的剩余容量或未投入的可供电电源,对失电区域内的待恢复负荷进行供电。需要注意的是,考虑到配电网的辐射状拓扑约束,多电源协调恢复所形成的连通域中仅能包含一个联络备用。

本文所述配电网非正常停运供电恢复策略的具体步骤如下所示。

步骤1:基于图论建立配电系统网络拓扑结构模型,初始化配电网中的各类设备参数。采用3.1节所述方法对联络备用进行容量等值,综合系统内的联络备用和DG,初始化失电区域内所有可供电电源,生成初始可供电电源集合{s1,s2,…,sq,…,snq},其中nq为可供电电源数量。

步骤2:在可供电电源集合中选择任意一个电源sq(q∈{1,2,…,nq}),求取负荷容量满足电源sq容量约束的可行恢复负荷子集,生成多个“电源—负荷”对。

步骤3:针对电源sq的各个“电源—负荷”对,采用与文献[25]中相似的Dijkstra算法求解该电源到各个“电源—负荷”对中相应负荷的最短路径,并查找相应路径节点上的所有设备,生成电源sq的可行恢复过程集合{φsq,1,φsq,2,…,φsq,mq,…}。其中,φsq,mq是电源sq可行恢复过程集合中的第mq个子过程的设备集合,包含该过程供电路径上的所有设备。

步骤4:选择电源sq可行恢复过程集合中的任意子过程φsq,mq,判断该过程的供电路径是否满足电压电流约束。若满足,则计算该子过程的恢复收益值;若不满足,则重新选取新的子过程进行判断。对可行恢复过程集合中的所有子过程重复上述操作,可保证恢复方案潮流不越限。对于满足约束的可行恢复过程,基于贪心策略求取恢复收益最大的子过程作为当前电源sq的最优备选子过程。

步骤5:选择可供电电源集合{s1,s2,…,sq,…,snq}中未被遍历的电源,重复步骤2至步骤4,求出各个电源单独投入时的最优备选子过程。基于贪心策略选取其中可获得最大恢复收益的单一电源,将该电源的最优备选子过程作为当前过程的最优化方案。

步骤6:排除失电区域内已恢复供电的负荷,更新系统拓扑结构,生成新的负荷停电区域及对应的可供电电源集合,重复步骤2至步骤5,直至无法生成新的恢复子过程,得到初步供电恢复方案。如果在采用初步恢复供电方案后,所有失电负荷均已恢复,则恢复方案满足要求,退出流程;否则转步骤7。

步骤7:针对初步恢复供电后的配电网,对形成的各个恢复区域剩余容量进行容量等效,将等效电源与未投入的电源一起作为可供电电源。选择失电区域内任意一个待恢复负荷wl(l∈{1,2,…,nl}),其中nl为待恢复负荷总数,求取电源容量满足负荷wl容量约束的所有可供电电源子集,生成多个“负荷—电源”对。采用Dijkstra算法求解该负荷到“负荷—电源”对中相应电源的最短路径,生成负荷wl的可行恢复过程集合。计及各类约束条件,基于贪心策略求取目标函数最优负荷wl的备选子过程。

步骤8:选择失电区域内未被遍历的停电负荷,重复步骤7,求出各个负荷单独恢复的最优备选子过程。基于贪心策略选取其中可获得最大恢复收益的待恢复负荷,将该负荷的最优备选子过程作为当前过程的最优方案。

步骤9:排除失电区域内已恢复供电的负荷及相应的供电电源,更新系统拓扑。重复步骤7和步骤8,直至无法生成新的恢复方案,从而得到配电网非正常停运后的最终供电恢复方案。

4　算例分析

因为本文研究内容是配电网的故障恢复决策,所以设备故障概率和负荷重要度的评估等并非本文研究重点,故将其固定为确定的输入量。

4.1　IEEE 3馈线系统算例

本文首先对IEEE 3馈线系统进行算例分析。该系统包括3个设置在电源节点出线侧的断路器A,B,C;3个常开的备用联络开关S14至S16;13个分段开关S1至S13;1台具有黑启动能力的DG(DG1);节点1至13上所接负荷均为可控负荷,各节点上对应有相应的负荷和DG控制开关(QL1至QL13、QLDG),系统结构如图1所示。假设开关S5和母线15之间的线路发生故障,将母线15出线侧的断路器B及分段开关S5断开以隔离故障,导致图1中虚线区域停电。

图1　IEEE 3馈线配电系统Fig.1　IEEE 3-feeder distribution system

系统故障备用容量一般为电力系统最高负荷的20%～25%[26],本算例中取系统最大出力的25%作为系统备用容量。在该非正常停运情况下,失电区域可供电电源总容量为12.83 kW,失电负荷总量为15.1 kW,失电区域的可供电电源及失电区域负荷数据详见附录A表A1。

根据第3节所述配电网恢复策略对该区域进行供电恢复方案的优化,为保证风险指标与收益指标处于同一数量级,取参数μ=17。定义投入可供电电源容量占可供电电源总容量的比例为可供电电源的投入率。将本文恢复策略的多过程优化方案与采用枚举法求得的全局最优的多过程优化方案进行对比,结果如表1所示。可以看出,两者恢复过程和供电路径均相同,表明本文采用的基于贪心策略的启发式搜索方法能够得到与全局最优解近似的优化方案,但本文恢复策略的计算时长远小于枚举法,计算效率更高。

表1　本文恢复策略与枚举法求得的多过程优化方案对比Table 1　Comparison of multi-process optimization scheme between proposed restoration strategy and enumeration method

在同样采用联络备用容量等值方法的基础上,将本文恢复方案和采用文献[27]中基于广度搜索的孤岛划分策略所得方案进行对比。本文恢复方案投入电源线路1和DG1,恢复节点2,8,9,10,恢复电量共计10.1 kW,占失电负荷总量的66.89%,可供电电源的投入率为86.75%,综合恢复收益指标为28.97;而快速孤岛方案投入电源DG1,恢复节点8,9,10,仅恢复电量6.1 kW,占失电总负荷的40.40%,可供电电源的投入率为64.69%,综合恢复收益指标为24.78,均小于本文恢复方案。

可见,在同样都无法恢复失电区域内所有负荷的情况下,基于广度搜索的快速孤岛恢复方法由于没有考虑电源与其他恢复区域富余容量进行协调恢复的可能性,无法充分利用失电区域的联络备用和DG电源使负荷恢复最大化;而本文所提恢复策略能够充分利用失电区域的可供电容量,协调恢复区域内的各类型可供电电源进行恢复操作,保证在有限供电容量下恢复负荷量和恢复收益的最大。

为了研究综合恢复收益评价体系中负荷重要度、风险因素对恢复方案的影响以及分析恢复方案对设备停运概率的敏感度,本节设置了3种优化模型进行恢复方案的求解和比较。

方案A:按照本文所提综合恢复收益目标求解得到。

方案B:不考虑本文目标中的负荷重要性求解得到。

方案C:不考虑本文目标中的负荷重要性和风险因素求解得到。

其中,方案A的恢复负荷量、可供电电源投入率及综合恢复收益如前文所述,其恢复过程中的风险指标为1.75;方案B投入电源线路1、线路3、DG1,恢复节点7,8,9,10,恢复电量共计11.1 kW,占失电总负荷的73.51%,可供电电源投入率为100%,均大于方案A中的相应值,其恢复过程中的风险指标为1.13,也优于方案A中的1.75,但由于该方法没有优先恢复重要负荷,其恢复收益为26.38,小于方案A中28.97的恢复收益;恢复方案C投入电源线路1和DG1,恢复节点7,8,9,10,恢复电量共计11.1 kW,占失电总负荷的73.51%,可供电电源投入率为86.75%,均大于或等于方案A中的相应值。但其恢复过程中的风险指标为2.38,远大于方案A和B中的风险指标,而恢复收益为26.00,均小于方案A和B的恢复收益。上述实验结果详见附录A表A2和表A3。

上述实验结果表明,配电网供电恢复策略优化过程中,是否考虑负荷重要性对恢复方案的真实收益有很大影响。不考虑负荷重要性的策略优化得到的恢复方案有可能获得较大的负荷恢复容量,但这些负荷可能是那些供电可靠性要求不高、供电保障级别较低的负荷,它们提前恢复供电的实际价值或意义并不大。恢复供电过程中,无视负荷中断供电带来的人身安全威胁、造成的经济损失和电力生产企业保供电需求的差异,将每个负荷的单位容量的停电损失等同看待,无疑会限制恢复过程中有限备用容量的高效、合理利用。另外,仿真结果还表明:如果在配电网供电恢复方案的求解过程中不考虑风险因素,得到的结果可能存在较大的风险,会更易于发生相继故障引起停电范围的扩大。本文所提恢复策略兼顾收益和风险,可以保证重要负荷的优先恢复,实现真实恢复收益的最大化,也可以有效减少配电网在实际恢复和运行过程中产生的不确定性损失,提高供电可靠性,保证负荷恢复量维持在较高的水平,获得综合最优的恢复方案。

为研究设备非正常停运概率对配电网故障恢复方案的影响,同时验证模型的实用性,本文也比较了设备不同停运概率对配电网故障恢复方案求解的影响,如表2所示。当开关S6和S7的设备非正常停运概率由0.000 96减小到0.000 16时,配电网故障恢复方案发生了变化;当开关S8的非正常停运概率由0.000 16增加到0.000 18时,配电网故障恢复方案同样发生了变化。这一结果表明,设备非正常停运概率的变化会对方案优化结果造成较为显著的影响,动态、准确的设备非正常停运概率模型研究尤为必要。

表2　基于非正常停运概率敏感性分析的故障恢复方案对比Table 2　Comparison of different restoration schemes based on unscheduled outage probability sensitivity analysis

4.2　典型8馈线配电网算例

为了进一步比较不同恢复方法的优劣,本节针对某典型配电网[28]加入DG后的算例模型进行分析。该配电网为8馈线39节点系统,包含8个位于电源出线侧的断路器、7个常开联络开关、31个位于母线进线侧的分段开关(S1至S31)、33个负荷和DG控制开关(QL1至QL31、QLDG1和QLDG2),1台具有黑启动能力的DG以及31个负荷,其结构如图2所示。

图2　典型8馈线配电系统Fig.2　A typical 8-feeder distribution system

假设线路A在节点3和9之间发生故障,导致线路A下游供电区域停电。本算例对虚线区域内的失电负荷进行恢复,该区域可供电电源总容量为127 kW,失电总负荷为112 kW,其中失电区域的可供电电源及负荷具体数据详见附录A表A4。根据本文所提主动配电网恢复策略,利用配电网非正常停运恢复决策系统对该算例进行恢复方案的求解,所得多过程优化方案如表3所示。采用文献[8]中的启发式方法求解恢复方案,并将结果记为方案D。另外,如果在本文策略中不考虑当前恢复过程供电路径对后续恢复过程供电路径的限制而忽略罚函数,将根据该方法得到的恢复方案记为方案E,3种恢复方案的结果如表4所示。相对于其他2种方法,本文策略求得的方案可恢复更多的负荷。为了进一步比较3种求解算法的优劣,将3种恢复方案代入本文不计及罚函数时的综合收益中,计算各方案的恢复收益(见表4),本文策略求得的方案仍然可以获得最大的恢复收益,这充分说明本文恢复策略中罚函数的引入可以有效避免陷入方案E中局部最优解。

表3　基于本文恢复策略的多过程优化方案Table 3　Multi-process optimization scheme based on proposed restoration strategy

由此可见,本文所提配电网恢复策略不仅可以充分利用失电区域内的各类可供电电源、最大化恢复负荷供电容量,而且在经济量纲下考虑了恢复方案的收益、代价与恢复过程中的不确定性风险,实现了恢复方案的经济收益最优。此外,本文所述策略通过引入考虑路径搜索限制的罚函数,能够在一定程度上改善启发式算法在搜索过程中易陷入局部最优解的缺陷,更有利于配电网故障恢复问题的全局优化求解。

表4　本文所提恢复策略同其他方法结果的比较Table 4　Comparison of results between proposed restoration strategy and other methods

5　结语

本文综合考虑负荷的恢复收益、恢复操作的控制代价及恢复过程中的不确定风险,建立了货币量纲上的配电网恢复多目标优化模型,并采用基于贪心策略的启发式算法对配电网恢复问题进行了优化求解。通过本文策略求解得到的配电网供电恢复方案,在一定程度上提高了配电网的供电可靠性和恢复过程的经济性。

由于采用了容量等值简化以及启发式优化算法,受开环运行准则的影响,因此所提故障恢复策略更适用于具有较多DG和少量联络备用的配电网。本文从模拟无后效性算法的贪心策略入手,通过引入罚函数在一定程度上改善了启发式搜索易陷入局部最优解的缺陷,但如何进一步确保全局最优恢复方案的获取,还有待更深入的研究。

本文得到智能电网保护和运行控制国家重点实验室资助,同时得到王昊昊、李威的指导,谨此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。