关于连通误报容错支配集的一个启发式算法

李有浩,赵承业,董合德

(中国计量大学 理学院,浙江 杭州 310018)

图的支配问题在图的相关研究中一直是一个很热门的分支,因为其具有很多的变形和实际的相关应用,从理论到算法[1-2],各种论点层出不穷.而连通支配集[3]就是图支配的一个重要分支问题.定义集合C⊆V(G),G(C)是集合C在图G=(V,E)中的生成子图,N(v)表示顶点v所有邻居节点,N[v]=N(v)∪{v}如果满足1)|N[v]∩C|≥1,∀v∈V(G),2)G(C)是连通的,那么就称集合C是图G的连通支配集.相关的研究也有很多,如文献[4,5].

误报容错支配集是图的支配问题的一个新的有趣的延伸[6-10],从容错的角度来看,其实是介于图的2-tuple支配和3-tuple支配之间的一个图的支配问题.这个问题最早是由Slater在2009年提出的[7],其实际意义可以对应社交网络中如下的一种情况.

我们对于一般的社交网络可以用图G=(V,E)来表示,图G中的每一个点代表一个社交个体,如果两个个体之间可以相互交换信息的话,那么就给这两个个体所对应的图G中的点连上一条边.这里假设图G中的每一个点都可能是一个入侵节点,例如一个着火点或是一个破坏者等等.假设存在这样的入侵者点v′.网络中还存在具有保护装置的点,它可以检测出其邻居节点是否是入侵节点,并且汇报这一入侵点的位置.要求尽可能布置最少的保护节点,而且还能准确找到网络中的入侵节点.这在网络的拓扑图中,相当于找到最小的满足条件的支配集D,在D中所有的点布置保护装置.然而这样的保护装置可能会损坏而不会汇报信息,为了使其能继续准确找到入侵点,这样的支配集D必须是双支配集.此外,这样的保护装置可能会汇报假的信息,这个时候即使D是双支配集也可能不能准确的找到入侵的节点.为了解决这一问题,Slater提出了误报容错支配集这一概念,并且证明下面的引理[7].

引理1:集合L是图G的一个误报容错支配集当且仅当:

1)集合L是图的一个双支配集;

2)对于图G中的任意一对节点u,v,都有|(N[u]∪N[v])∩L|≥3.

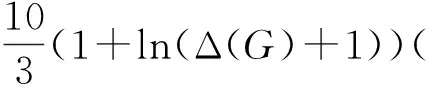
1　连通误报容错支配集问题精确算法

连通的误报容错支配集问题已经被证明是属于NP-完全问题[9],即很难找到这种问题的多项式时间的算法.这节给出一般图上构造最小连通误报容错支配集的精确算法,算法的思想就是根据连通误报容错支配集的定义,对所有的点进行遍历判断.

对于一般的连通图(顶点数超过3)G=(V,E),顶点数为n,算法是从寻找其最小的双支配集开始.

1)利用整数规划求得图G的最小双支配集的顶点数s.

2)求得所有从n个点中选取s个点的组合集D.

3)遍历D中所有的集合L,判断集合L是否满足双支配、点对三支配、子图连通的条件,如果都满足跳出循环,输出集合L.

4)如果遍历完D中所有的集合都不能满足其是连通误报容错支配集的三个条件,则令s=s+1,并转到步骤2继续循环.

由于这里用到的是遍历判断的思想,对于每一个点的情况,其可能属于支配集,也可能不属于支配集,所以算法的复杂度为O(2n).

2　连通误报容错支配集问题的启发式算法构造

这节提出了构造一般连通图上的连通误报容错支配集的一种基于贪婪策略的多项式时间启发式算法.

2.1　问题描述及符号表示

问题描述:设图G=(V,E),n=|V|为图的节点数.找到图G的一个集合L,保证其图G的连通误报容错支配集的前提下,使L的节点数尽可能的少.

符号说明:在算法执行过程中,节点和节点对的状态都可能发生变化.节点可能出现未定义,1-被支配,2-被支配,支配这4种状态;节点对可能出现未定义,1-被支配,2-被支配,3-被支配这4种状态.假定在算法初始阶段,所有节点和节点对状态均为未定义.设当前操作节点为v,定义关于节点v的下列符号:

L0:节点状态为未定义的节点集合.初始时,L0=V.

L1:节点状态为支配的节点集合.初始时,L1=Ø.

L2:算法执行过程中当前的节点状态为1-被支配,2-被支配的节点集合,其也是可能成为支配点的集合.初始时,L2=Ø.

d0(v):N[v]中状态为未定义的节点个数.

d1(v):N[v]中状态为1-被支配的节点个数.

d2(v):N[v]中状态为2-被支配的节点个数.

P0:状态为未定义的节点对集合.

P1:算法执行过程中当前节点对状态为1-被支配或2-被支配的节点对集合.初始时,P1=Ø.

P2:状态为3-被支配的节点对集合.初始时,P2=Ø.

d0(pv):节点v闭领域内的节点对中状态为未定义的节点对数.

d1(pv):节点v闭领域内的节点对中状态为1-被支配或2-被支配的节点对对数.

规则描述:在算法执行过程中,状态为支配的节点的闭邻域内的节点状态也会发生变化,同时需要选择新的支配节点,直到满足条件,具体规则如下:

规则Ⅰ设节点v为支配节点,则任意一非支配节点u∈N[v]的状态变化如下:

1)若节点u的当前状态为未定义,则其状态变为1-被支配;

2)若节点u的当前状态为1-被支配,则其状态变为2-被支配.

规则Ⅱ设节点v为当前支配节点,选择新的支配节点的规则如下:

1)找出L2中d0(u)最大值所对应的节点u,若节点u唯一,则将该节点作为新的支配节点,否则把这些节点放入一个集合里,记为D0(v),转入2);

2)找出D0(v)中d1(u)最大值所对应的节点u,若节点u唯一,则将该节点作为新的支配节点,否则把这些节点放入一个集合里,记为D1(v),转入3);

3)找出D1(v)中d2(u)最大值所对应的节点u,若节点u唯一,则将该节点作为新的支配节点,否则取这些节点中序号较小者作为新的支配点.

规则Ⅲ若所有节点均为2-支配,部分节点对未满足3-支配,选择新的支配节点规则如下:

1)找出L2中d0(pu)最大值所对应的节点u,若节点u唯一,则将该节点作为新的支配节点,否则把这d1(pu)些节点放入一个集合里,记为P0(v),转入2);

2)找出P0(v)中最大值所对应的节点u,若节点u唯一,则将该节点作为新的支配节点,否则取这些节点中序号较小者作为新的支配点.

2.2　算法构造

这节给出的连通误报支配集的启发式算法的主要思想是:首先使图中的任意节点的状态变化为2-被支配,继续添加新的支配点使图中所有的节点对状态变为3-被支配.其中第一步是基于最小生成树的思想,对图G设置集合S来放置支配节点,集合V-S中与集合S邻接且度数相对较大的节点优先考虑最为支配点.不断的重复这样的操作,直到所有的节点状态都是2-被支配或支配节点状态;第二步从所有的节点中,以为满足3-被支配的节点对数目最大作为贪心选择标准来选择新的支配点加入到集合S中,直到所有的节点对状态都为3-被支配.下面是相关的算法描述.

步骤1构造节点2-支配集

1)在图G中选择节点度最大的节点(若度最大节点不唯一,则选择序号最小的节点)作为初始支配节点v0,把节点v0从集合L0中取出,放入集合L1中,按照规则Ⅰ改变N[v0]的节点状态.并且更新集合L0,L2,将状态为1-被支配的节点从集合L0中取出,放入集合L2中.

2)在集合L2中的所有节点,按照规则Ⅱ选择新的支配点,并作为当前操作节点v,按照规则Ⅰ改变N[v]中所有非支配节点的状态.更新集合L0,L1,L2,即将节点v从L2取出,放入到集合L1中;将状态为1-被支配的节点从L0中取出,放入到集合L2中.

3)若图G中非支配的节点均为2-被支配,则算法结束,否则转2)继续执行.

步骤2构造节点对3-支配集

1)根据当前图G中的节点对的状态,更新集合P0,P1,P2.

2)在集合L2中的所有节点,按照规则Ⅲ选择新的支配点,并作为当前操作的节点v,将该节点v从L2L2中取出,放入集合L1中.

3)若图G中的节点对状态均为3-被支配,则算法结束,否则,更新集合P0,P1,P2,转2)继续执行.

定理1:根据规则Ⅰ、Ⅱ、Ⅲ经过构造节点2-支配集和节点对3-支配集得到的集合L1就是图G的一个连通误报容错支配集.

证明:首先证明集合的连通性.在构造2-支配集时,除了初始节点,新的支配节点都是从L2中选取,即被支配的节点集合.保证新的支配节点总是与L1中至少一个节点相连接,因此最后得到的2-支配集就是连通的集合.同样在构造3-支配集时,新的支配点也是从L2中选出,因而得到的节点对3-支配集即最后得到的集合L1是连通的;其次证明集合L12-支配图G中所有的节点,即|N[v]∩L1|≥2,∀v∈V(G).在步骤1执行后得到的集合L1,其2-支配图G中所有的非支配集节点,而对于L1中的节点,由于连通性的保证,所以有|N[v]∩L1|≥2,∀v∈L1.最后证明集合L13-支配图G中的所有节点对,即|(N[u]∪N[v])∩L|≥3,∀u,v∈V(G)(u≠v).由算法步骤2最后的终止条件可以知道最后得到的L1一定3-支配所有的节点对;否则算法一直进行下去,因而图中所有的节点对的状态最后都是3-被支配.

综上2.2所提出的算法最后得到的就是图G的一个连通误报容错支配集.

3　算法分析及实现

算法的步骤1形成2-支配的节点集合,按规则Ⅰ更新支配节点邻域内邻接节点状态的时间复杂度为O(n),更新节点闭邻域内的节点状态的时间复杂度为O(n2);按规则Ⅱ选取的新的节点的时间复杂度为O(n),则构造2-被支配的节点结合的时间复杂度为O(n3).算法步骤2形成节点对3-被支配集,更新各节点闭邻域的节点对数的时间复杂度为O(n2);按规则Ⅲ选取新的支配节点的时间复杂度为O(n),则构造节点对3-支配集的时间复杂度O(n3).综上,2.2提出的启发式算法的时间复杂度为O(n3).

对本文提出的基于贪婪策略的连通误报容错支配集启发式算法进行仿真实验,测试所用的无线传感器网络随机图通过如下方式产生:在500×500的平面内,随机产生n个节点,假设这样的无线传感器网络每个节点的通信半径是相同的,记为R,如果两个节点的距离不大于R,则认为这两个节点是有边连接的.如果构造得到的图不是连通的,那就重新构造,直到构造的图连通为止.现在以节点数n为150,节点之间的通信半径80为例,用图来说明构造的连通误报容错支配集的过程.(如图1)图中用蓝色节点表示被支配节点,红色节点表示形成节点2支配产生的支配节点,用黑色节点表示形成节点对3-支配集产生的支配节点.从图中可知,所得到就是图G的一个连通误报容错支配集.

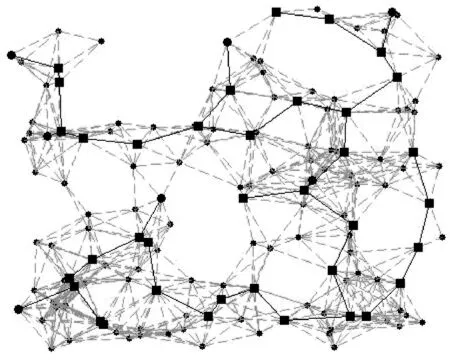
图1　连通误报容错支配集构造Figure 1　Construction of connected liar’s dominating set

为体现文中提出的启发式算法的计算效率和最终得到连通误报容错支配集和最优值之间的误差大小,我们对精确算法和启发式算法进行了仿真(表1),仿真的图也是基于计算机随机生成的连通图,图的生成算法以及具体结果如下.

实验所用图的生成算法:

1)在500×500的平面内,随机生成n个顶点.

2)两个节点之间的距离小于100,就连接两个节点.

3)用深度优先搜索判断生成的图是否连通,连通则输出该图,否则跳到步1)精确算法和启发式算法对应的结果如下.

表1　启发式算法的相关实验结果

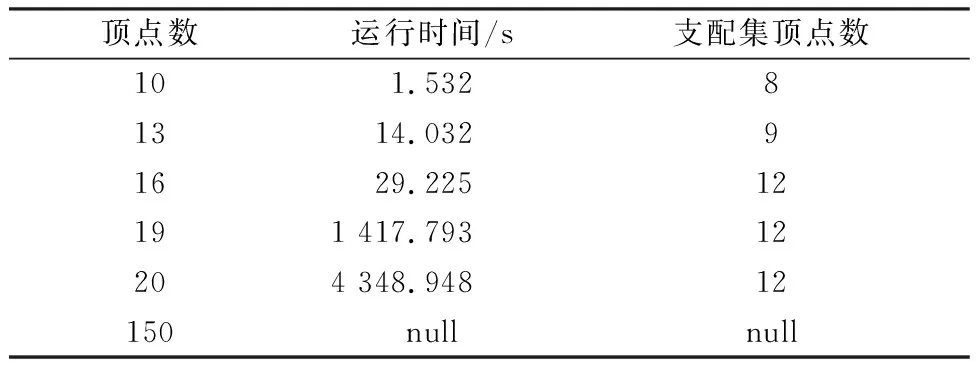
表2　精确算法的相关实验结果

从表2中可知,由于精确算法的复杂度比较高,因此我们可以得到精确解的网络规模大小比较有限.通过表1和表2比较,我们可以看到启发式算法在计算时间和网络规模上具有很大的优势,其结果和精确解比较差距较小.

仿真实验所用计算平台:CPU酷睿i5-7200u,内存8 G,硬盘SSD 256G.

4　总结与展望

本文先是提出了一个连通误报容错支配集问题的精确算法,并证明了其计算复杂度是指数型.随后给出了该问题的一个时间复杂度为O(n3)的启发式算法,最后通过计算机模拟实现两个算法,并从运行时间和准确度上比较两个算法.文中给出的算法属于集中式的算法,此外可以考虑分布式算法,对于局部的信息进行支配集构造,最后合并处理,这样计算的时间复杂度应该能降低.