民用飞机典型连接非规则结构的紧固件钉载分布研究

苟鹏坡，帅国武

（上海飞机设计研究院，上海201210）

0　引言

紧固件是飞机制造中最常用的连接方式，对于民用飞机中多紧固件连接结构的钉载分析，工程上主要采用解析法和有限元法进行计算。解析法对仅于简单、规则的连接结构可以得到比较准确的钉载分布。有限元法可以通过建模精确地得出大多数连接结构的钉载分布，但建模过程耗费时间较长，且一个模型只能针对单一结构进行分析。因此，针对实际结构中的非规则连接结构，需要得出一种可靠、快速、适用范围广的钉载计算方法。

1　连接非规则结构钉载分布的解析法

1.1　结构形式

单剪连接件非规则结构形式如图1所示。

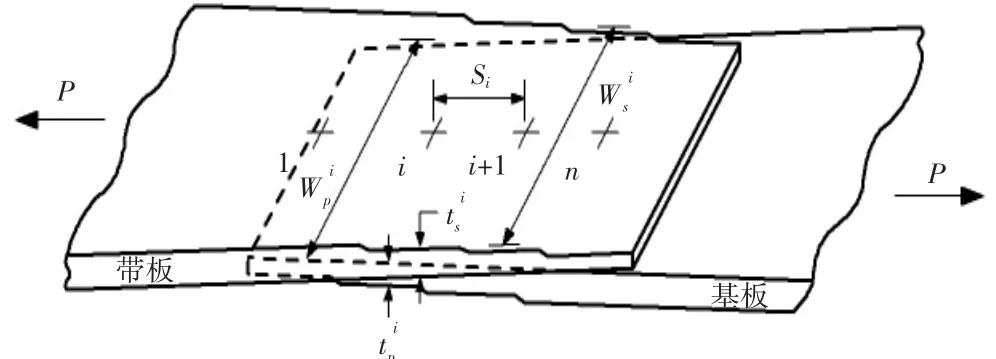
图1　单剪连接件非规则结构

图1中符号意义如下：

Si为第i颗钉与第i+1颗钉之间的间距（载荷方向）；n为钉排数；为第i颗钉与第i+1颗钉之间带板的厚度；为第i颗钉与第i+1颗钉之间基板的厚度；为第i颗钉与第i+1颗钉之间带板的宽度；为第i颗钉与第i+1颗钉之间基板的宽度；P为外载荷。

其他参数意义如下：

Ci为第i颗钉的柔度系数；为第i颗钉与第i+1颗钉之间带板的柔度系数；为第i颗钉与第i+1颗钉之间基板的柔度系数；Es为带板的弹性模量；Ep为基板的弹性模量；Ri为第i颗钉载荷。

1.2　基本假设

（1）结构均处在弹性范围以内；

（2）忽略摩擦力和装配间隙的影响；

（3）应力沿板横截面均匀分布。

1.3　变形协调方程

变形协调方程可以理解为任意相邻两钉之间的变形要协调，即其中一块板两钉之间钉的变形+板的变形=另一块板对应位置两钉之间钉的变形+板的变形。

对于单剪连接件，其钉变形、板变形以及板上载荷如图2所示。

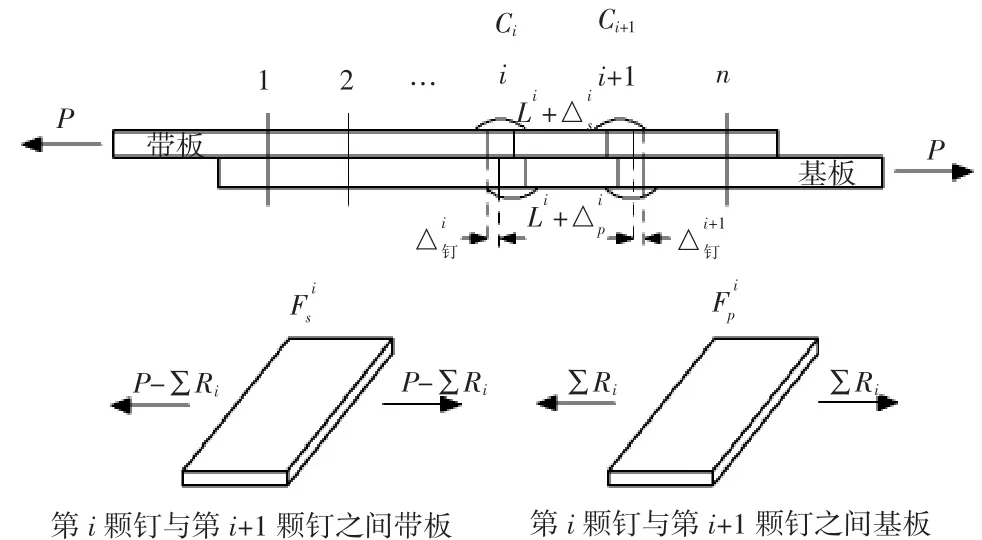
图2　单剪连接件的变形协调关系

因此，可得第i颗钉与第i+1颗钉间的变形协调关系：

其中，第i颗钉与第i+1颗钉间带板上的载荷为P-∑Ri，基板上的载荷为∑Ri，则第i颗钉变形、第i+1颗钉变形、带板变形和基板变形分别为：

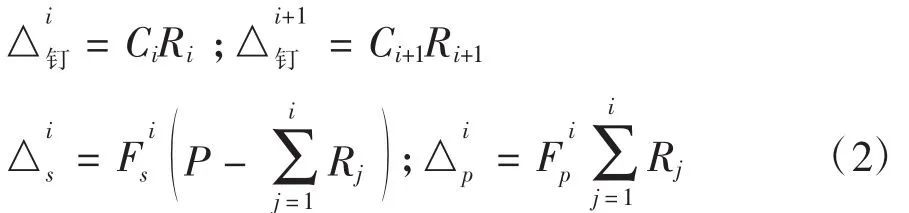
将钉载荷Ri均放于等式右侧，仅外载荷P在等式左侧进行化简，可得下面n-1个方程：

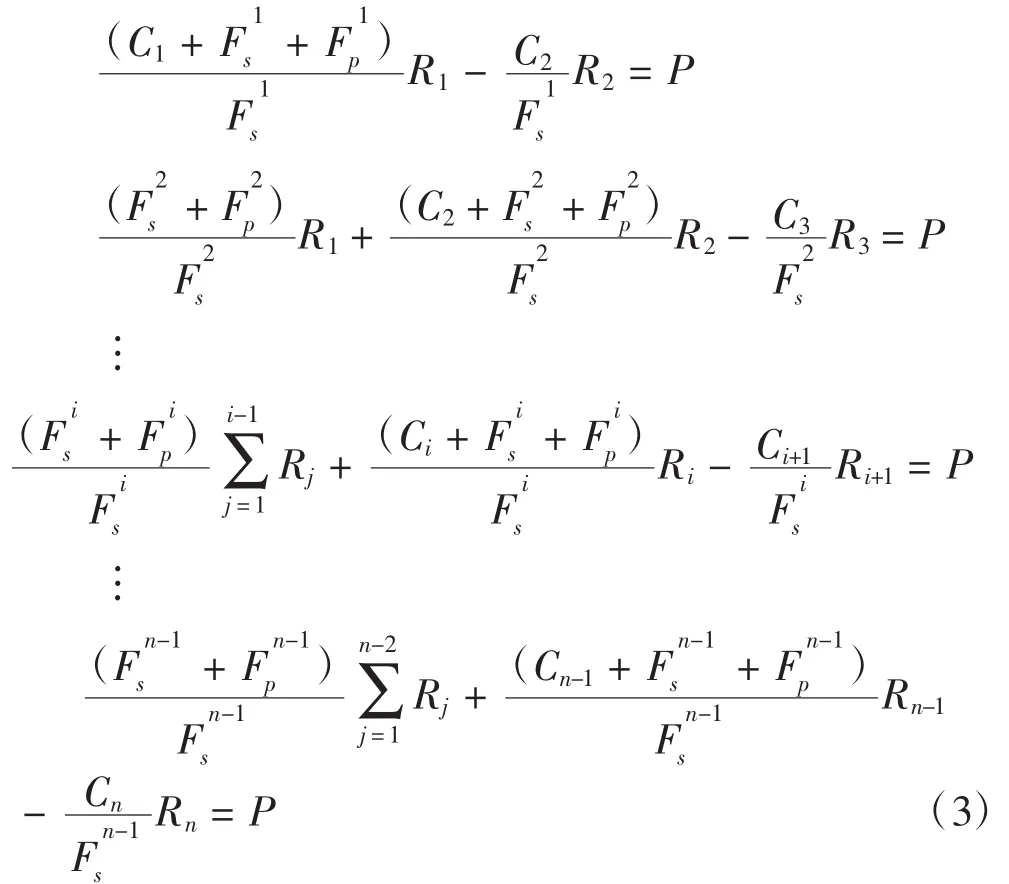
1.4　力的平衡条件

力的平衡条件是指各钉载荷之和应与外载荷相等，其表达式如下：

结合前面n-1个方程，外载荷P取1，即可求出各钉载荷与外载荷之比Ri/P.

1.5　柔度系数工程计算方法

根据前面的分析，钉载分布与各钉的柔度系数Ci、各块带板柔度系数和基板柔度系数有关，下面给出工程上钉柔度系数和板柔度的计算方法。

1.5.1钉柔度系数

根据参考文献[1]，对于如图3所示的单剪连接，其连接板均为铝合金材料时，可按下式确定其钉柔度系数C：

图3　单剪连接的钉柔度系数

式中各参数意义如下：

t1为较薄板的厚度；t2为较厚板的厚度；Kdc为钉材料修正系数。对于铝钉，Kdc=1；对于钛钉，Kdc=0.77；对于钢钉，Kdc=0.67.

1.5.2板柔度系数

根据参考文献[1]，带板柔度系数Fs和基板柔度系数Fp的公式如下：

2　典型连接非规则结构钉载分布的解析法验证

2.1　验证方法

由于有限元法可以很好地通过建模来模拟近似非规则结构（钉直径、钉间距、板宽和板厚不同的结构），因此将用参考文献[2]和[3]中介绍的有限元法得出4种非规则结构的钉载分布，用来验证本文中的典型连接非规则结构钉载分布的解析法的适用性。4种非规则结构均只改变了单剪连接规则结构的一类参数，单剪连接规则结构具体参数见表1，有限元模型见图4，连接结构简化为板梁系，一端固支，一端加均布载荷，非规则结构建模过程与规则结构相同，仅修改了模型的几何参数。

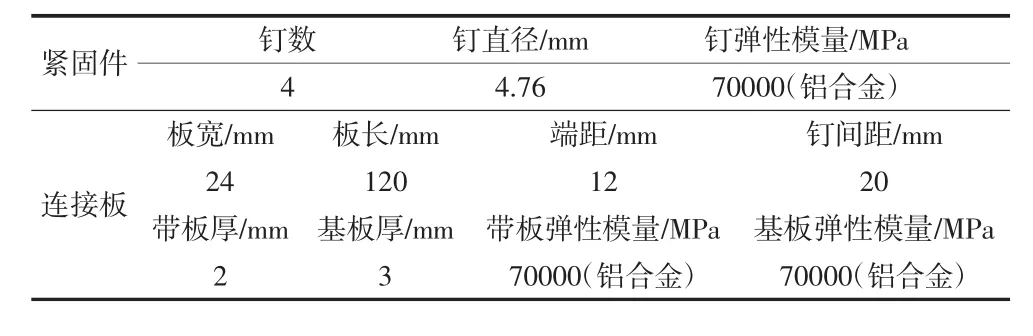
表1　单剪连接规则结构算例参数

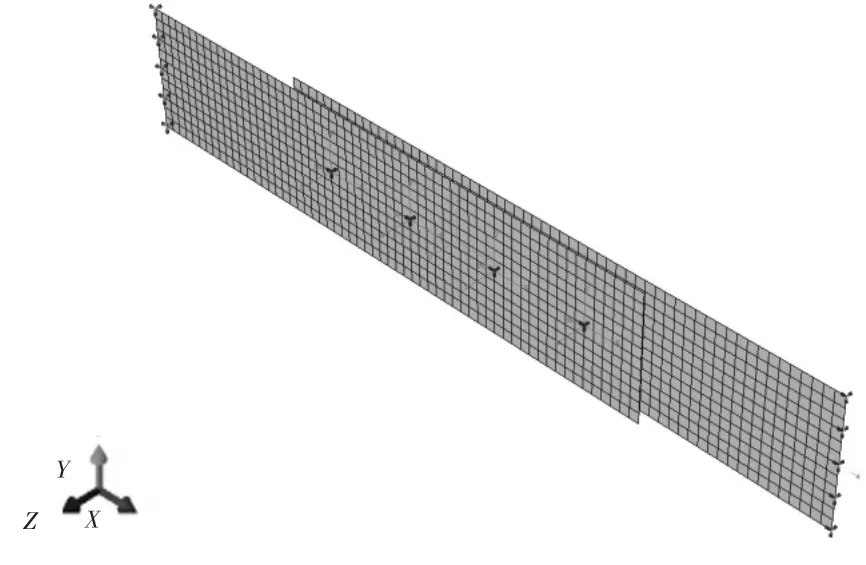
图4　单剪连接规则结构算例的有限元模型

2.2　单剪连接非规则结构

2.2.1钉直径不同

对于钉直径不同的验证算例，相对于表1中的单剪连接算例，仅D1为5.56 mm，本文解析法和有限元法得到的结果对比见表2.

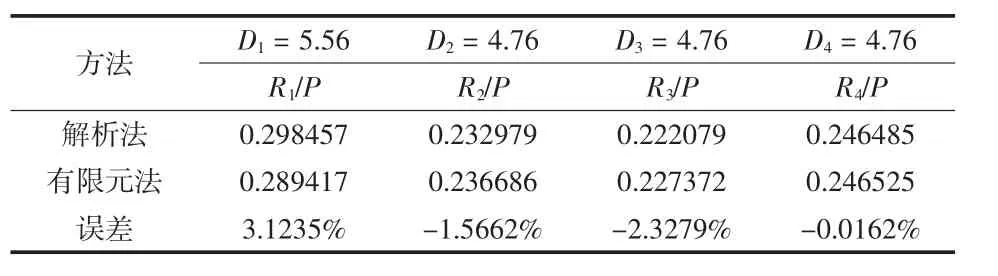
表2　钉直径不同时的结果对比

2.2.2钉间距不同

对于钉间距不同的验证算例，相对于表1中的单剪连接算例，仅S1为24 mm，本文解析法和有限元法得到的结果对比见表3.

表3　钉间距不同时的结果对比

2.2.3板宽不同

对于板宽不同的验证算例，相对于表1中的单剪连接算例，带板端部至第1钉的板宽为16 mm，第1钉至第2钉间板宽线性递增至24 mm，第2钉至第3钉间板宽为24 mm，第3钉至第4钉间板宽线性递减至16 mm，本文解析法和有限元法得到的结果对比见表4.

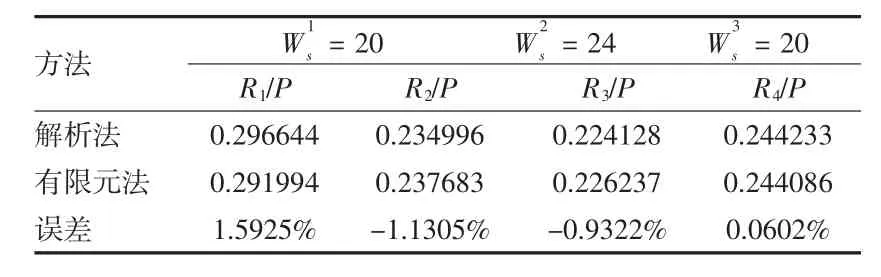
表4　板宽不同时的结果对比

2.2.4板厚不同

对于板厚不同的验证算例，相对于表1中的单剪连接算例，带板厚度由第1钉处2 mm线性递减至第4钉处1.1 mm，基板厚度由第1钉处3 mm线性递增至第4钉处3.9 mm，本文解析法和有限元法得到的结果对比见表5.

表5　板厚不同时的结果对比

2.3　验证结论

通过上述对比，可以看出，对于典型连接非规则结构，本文的解析法得出的钉载分布结果与有限元结果差异很小，误差最大为5.6%，精度满足工程要求。