转子部件的多相关激励排序试验与分析

李舜酩，孙明杰，姚省通，徐 坤

（南京航空航天大学能源与动力学院，江苏南京 210016）

0 引言

转子部件受到激励后通常有两个响应表现：弯曲振动系统和扭转振动系统[1]，转子系统的弯曲振动和扭转振动不仅有各自的固有振动特性，而且还存在一定程度的振动耦合[2]。而且，激励之间的相关性在一定程度上影响着振动响应信号的分析的准确性。因此，研究相关激励对转子部件的振动响应是非常必要的。但是转子系统弯曲、扭转振动耦合的研究尚不十分完善[3]。

随着对整车振动特性研究的进一步深入，这一影响已被更多人所关注，成为又一个研究发展方向。转子部件的激励之间的相关性，在一定程度上影响着振动响应信号的分析的准确性。因此，研究相关激励对转子部件的振动响应是非常必要的。

振动分析中一类很广泛的工程问题是以确定两组或几组数据之间的线性关系为中心的[4]，还有一类工程问题是以确定数据之间的线性关系为基础。这些线性关系一般有相关函数或谱密度函数来表示。相干函数是相关性从时域到时域的转换，可以由两个信号的谱密度函数得出，表示了一个信号对另一个信号的影响程度。相干函数分为常相干、重相干和偏相干[5]。在偏相干函数方法中，相关性输入下，决定输入之间的优先权是非常关键的。要成功的应用偏相干函数方法，应该根据物理意义和可用的信息来确定输入之间的优先权[6]。

结合多自由度系统的基本理论，相关函数、谱密度函数以及相干函数的基本理论，推导出3输入3输出的相关表达式。再结合车辆传动系部件实际振动情况，选取合适的结构件作为试验对象，并搭建相应的振动试验台，选取合适的振动频率进行试验。最后根据推导所得的表达式，运用MATLAB编写程序，对采集到的振动信号进行数据分析，得到多相关源激励对响应信号的影响。

1 多相关基本原理

在相干分析中，把多输入多输出模型分解为若干个多输入单输出模型来求解。对此次试验中的振动模型是3输入3输出系统，因而可以分成3个3输入单输出模型进行相干分析。3输入3输出系统如图1所示。

图1中，x1（t），x2（t）和x3（t）是相关的，但不是精确相关。在偏相干函数方法中，相关性输入下，决定输入之间的优先权是非常关键的。输入循序对错对偏相干分析有着决定性的影响，并决定了对结果的解释。在进行偏相干分析之前，首先要决定输入的优先顺序。理论分析时，可以先行假定优先输入的顺序[7]。假设图中输入的优先顺充是x1-x2-x3，系统关系式为：

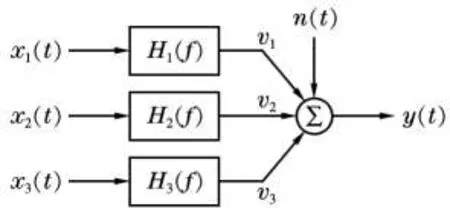
图1 多输入单输出系统

则该关系式可以转化成为特殊的单输入单输出模型。其中，互相干函数，S是功率谱，下标代表不同的条件。系统响应表达式如下：

对图1中x1（t），可认为其条件谱密度函数等于其谱密度函数；对x2（t），其条件谱密度是除去x1（t）影响的x2.1与其他输或输出之间的谱密度函数。其相干函数是除去输入x1（t）的条件随机变量x2.1与其他除x1（t）影响的条件随机变量之间的常相干函数[8]；对x3（t），其条件谱密度是除去x1（t）和x2（t）影响的x3.1，2与其他输入或输出之间的谱密度函数。其相干函数是除去输入x1（t）和x2（t）的条件随机变量x3.1，2与其他除去x1（t）和x2（t）影响的条件随机变量之间的常相干函数[9]。用Matlab编程求解，得到其条件输入和条件输出的功率谱和相干函数，如表1所示。

从而得到式（1）中的各项值。得到各个输入在输出中做出的贡献和影响得到各个输入在输出中做出的贡献和影响[10]。

3 试验研究

3.1 试件结构状态

试验对象由1个偏心圆盘和1个刚性轴相连，刚性轴两轴端通过轴承固支，其中一轴与可变速电机相连，如图2所示。几何参数：轴承之间距离225 mm，圆盘直径80 mm，厚度20 mm，圆盘离左右轴端距离分别为90 mm和115 mm。材料均为45号钢。

表1 条件输入条件输出的功率谱和相干函数表达式

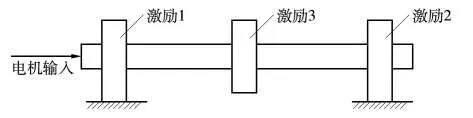
图2 轴和圆盘构成试验对象

3.2 试验目的、仪器与内容

本试验先通对轴进行两相关激励，验证采用偏相干方法的有效性。再通过对轴进行3相关激励，通过偏相干方法[11]分析轴的响应主要受哪些激励影响，即响应主要由哪些激励引起的。因此，本试验主要内容如下。

（1）分析车辆传动系传动轴横向振动的主要频率范围，从而确定激励频率范围。

（2）在（1）中选定的频率范围内，对轴两端进行相关激励，测量得响应信号。分析偏相干方的有效性。

（3）再对轴的两端进行相关激励，并通过电机驱动轴进行运转，使的中间偏心圆盘在高速旋转的过程中对轴产生横向激励，从而达到3相关激励的要求。

（4）测量到轴端3个激励信号，以及3个响应信号，对数据进行试验分析。分析各个响应受到的各个激励的影响情况。试验所用仪器：自行设计U形卡1个，ZT-3转子振动模拟试验台，转子，转子转速测量仪，手动调速电机，工程激振器2个，阻抗头2个，位移传感器，信号发生器KD5602，信号放大器KD5702，DH5922动态信号测试分析系统，计算机。

3.3 试验过程

根据前面的理论和试验室现有条件，设计了多相关激励的试验方案，简述如下。采用1个信号源连接1个三通转换接头，并通过两功率放大器，分别驱动2个激振器，一个激励器直接对轴的一端进行激励，另一激励器通过与设计的U形卡对轴的另一轴进行激励。第三个激励通过可变速电机驱动轴使的偏心圆盘进行转动，从而产生一个离心力，对辆的中间进行激励。试验示意图如图3所示。U形卡用来模拟具有非线性的系统，从而使得两个激励之间不完全相关。

在完成系统标定和可靠性检查后，开始进行测试。因为实际测量次数有限，本试验采用3次测量，再进行平均处理以减小试验误差。本试验的阻抗头通过M5的螺栓和螺杆与试验件相连，试验中应该避免在所关心的频率范围的前几阶振型的节点处激励，本试验在（10～1000）Hz频段内进行正弦扫描激励。多相关激励的实际试验台中的激振器安装位置和位移传感器以及U形卡的位置如图4和图5所示。

在图2中，分别以符号来代表试验中的激励与响应，如表2所示。

表2 各激励力和响应信号的符号对应关系

由于试验测试过程中，轴处于运转状态，故不可能对轴的圆盘处响应采用压电式加速度传感器测量，采用电涡流传感器进行测量，得到位移数据。

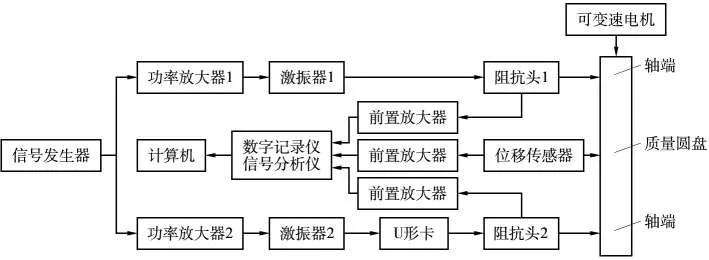
图3 试验方案示意

由式（3）和（4）可知，加速度信号是位移信号的连续二次求导，信号的频率不变，相位成变换180°，幅值为频率的平方倍。因此，为用位移信号与其他激励力信号在频域上讨论与加速度与激励力讨论是一样有效的。

4 试验数据分析

在试验数据分析上，多输入多输出系统等于多个多输入单输出的结合。因此，只要分析逐个响应，就可以分析出各个响应由哪些激励源构成。试验分析中，应用MATLAB软件分别对轴端和圆盘处的响应信号与多相关激励力之间的关系进行分析，其中圆盘处的激励力x3（t）利用驱动电机让圆盘定速3675 r/min转动产生。由于相关分析方法是针对x1（t），优先，x2（t）次之，计算 γ2y1（f）的值。再假设x2（t）优先，x2（t）次之，计算γ1y2（f）的值，进行比较，若在相同的频率点上的γ2y1（f），得到γ2y1（f）与γ1y2（f）相比较，在频率点上，哪个值大说明假设中的第二个输入起决定作用，说明该频率点优先[15]。优先权的确定如表3所示。

图4 多相关激励试验图

图5 U形卡

根据表3频率段得到的激励源的优先顺序，由matlab编程求得各个频率段上的条件谱图。求出圆盘处的响应的自谱及条件谱图6。由图可以看出，在某些谱峰处，其值相重合，说明这一点处于系统的某阶共振动频率，非线性较强，相干函数非常差，因此，造成所计算到的条件谱值相近。平稳随机信号的统计研究方法，故对所测量的到的信号要消除非零均值的影响[12]。

4.1 圆盘处响应信号与多相关激励力关系

首先分析圆盘处的响应信号与多相关激励之间的关系。车辆的弯曲振动主要关心的频率在低频范围，因此对试验结果分析频率为500 Hz以下。采用了偏相干分析相关激励与振源的影响，因此需要先进行划分多相关激励频率段和确定激励力优先顺序。本试验由于是传动轴结构的振动试验，考虑到常相干函数法、脉冲频响函数法和Hilbert法来决定频率点的输入优先权的优缺点及实用范围，采用可以在因果条件不明显的情况下应用的常相干函数法来分析3个输入的优先权[13-14]。

由于通过γy（f），γ2y（f）和γ3y（f）无法确定优先权的频率段，在常相干函数方法采用排除法对优先顺序进行排序。排除法为当两上输入x1（t），x2（t）因果关系不明确，无法排序时，即先假定

表3 各频率段处激励源的优先输入顺序

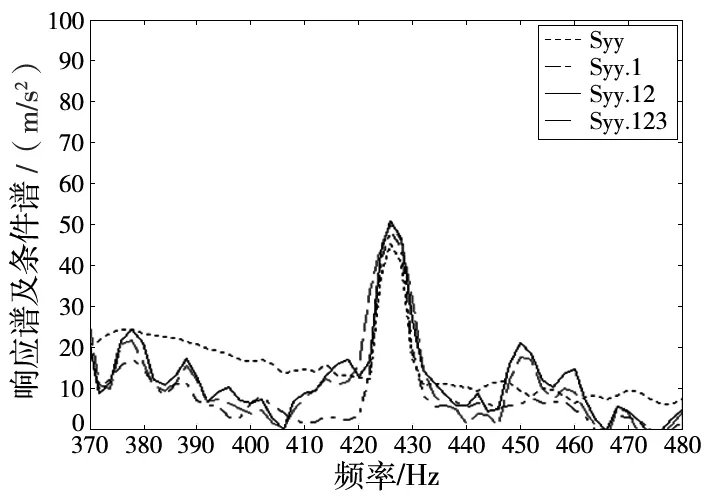
图6 频率段（370～480）Hz的响应的条件谱

4.2 轴端1处的响应与激励力之间的关系

按照4.1节的分析方法对轴端1处响应与各个激励力之间的关系。划分出的频率段及部分优先顺序后，根据上节提出的常相干排除法，得出3个频率段的优先输入顺序，如表4所示。由表4的频率段所列的顺序，得出条件谱如图7和图8。轴端2处的响应分析方法同以上分析相同，故在此不在继续分析。图表也不一一列出。

表4 各频率段处激励源的优先输入顺序

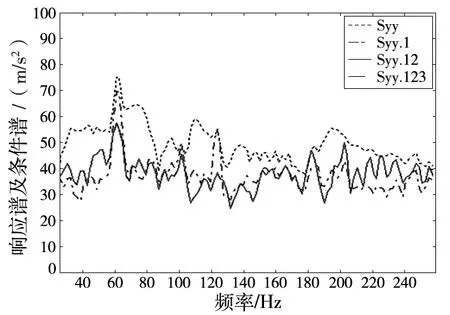
图7 频率段（25～255）Hz频率段响应条件谱

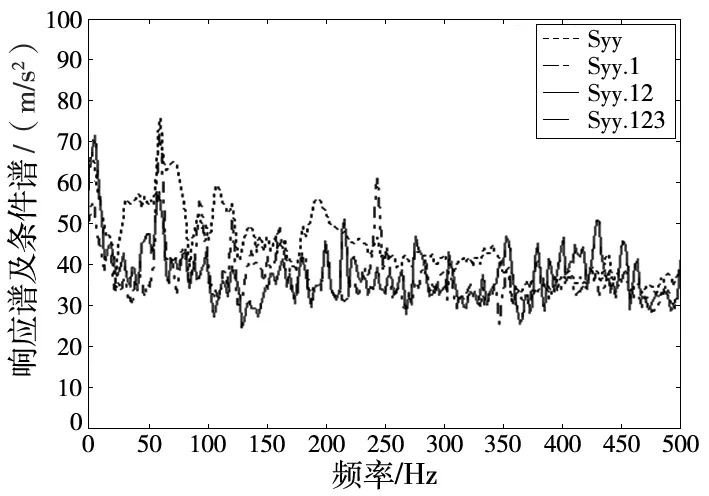
图8 频率段（255～450）Hz频率段响应条件谱

以上试验分析表明，在偏相干分析方法基础上，采用常相干函数法与排除法相结合，能够确定多相关激励源输入的优先顺序，求出响应的条件谱。试验分析检验了输入激励源顺序，从而确定响应点的主要激励源和次激励源，验证了多相关激励对响应的影响的理论。

5 结论

（1）介绍了相关函数、谱密度函数以及二输入单输出系统的相干分析的基本理论。并以此为基础推导了3输出单输出系统的相干分析理论。

（2）根据现有的试验室条件，设计并加工适合本试验需要的试验件：U形卡和轴座卡套。对试验仪器进行标定工作，保证了试验中所测到的数据有效。

（3）在偏相干分析方法基础上，采用常相干函数法与排除法相结合，确定了多相关激励源输入的优先顺序，求出响应的条件谱。分析验证了输入激励源顺序的正确性，从而确定响应点的主要激励源和次激励源，验证了多相关激励对响应的影响的理论

[1]左曙光，刘敬芳，吴旭东，王哲，相龙洋，张珺.车用离心风机转子系统振动特性分析[J].农业工程学报，2016，32（4）：84-90.

[2]李舜酩.振动模态分析[M].南京：南京航空航天大学出版社，2004.

[3]关卓怀，蔡敢为.转子弯扭耦合振动共振特征分析[J].噪声与振动控制，2016，36（1）：5-9，25.

[4]胡海岩，孙久厚，陈怀海.机械振动与冲击[M].北京：航空工业出版社，2002.

[5]宋晶，巢凯年，利用偏相干函数法识别汽车噪声源的研究[D].西安：西华大学，2006.

[6]何建，沈国华，王铁刚，汽车NVH特性概述[J].客车技术与研究，2007（5）：15-18.

[7]Ronghui ZHENG，Huaihai CHEN，Xudong HE.Control method for multi-input multi-output non-Gaussian random vibration test with cross spectra consideration[J].Chinese Journal of Aeronautics，2017.

[8]J.S.Park and K.J.Kim.Determination of priority among correlated inputs in source identification problems[J].Mechanical Systems and Signal Processing，1992（6）：491-502.

[9]A.Papoulis.TheFourierIntegraland ItsApplications[M].New York：McGraw-Hill，1962.

[10]Y.Qiu，M.J.Griffin.Transmission of vibration to the backrest of a car seat evaluated with multi-input models[J].Journal of Sound and Vibration，2003，274（1）.

[11]Zulkifli Mohd Nopiah，Ahmad Kadri Junoh，Ahmad Kamal Ariffin.Vehicle interior noise and vibration level assessment through the data clustering and hybrid classification model[J].Applied Acoustics，2015，87.

[12]Belhadef Rachid，Ahmed Hafaifa，Mohamed Boumehraz.Vibrations Detection in Industrial Pumps Based on Spectral Analysis to Increase Their Efficiency[J].Management Systems in Production Engineering，2016，21（1）.

[13]李舜酩，郭海东，李殿荣.振动信号处理方法综述[J].仪器仪表学报，2013，34（8）：1907-1915.

[14]张袁元.车辆多相关振动噪声源及其路径识别方法研究[D].南京：南京航空航天大学，2013.

[15]De Tian，Wei He，Ning Bo Wang.Effect of Coherence Function on RotationalFourierSpectrum ofWind Turbine[J].Advanced Materials Research，2013，2114（608）.