基于降维处理的MUSIC二维DOA估计算法

张铁峰，吉波

（1 中国电子科技集团公司第二十研究所，西安 710068；2中国人民解放军驻210所军事代表室，西安 710065）

0　引言

在雷达、声纳、高精度卫星导航定位、无人机自主着陆以及高灵敏度设备的检测等领域，需要对实际工作环境中的电磁信号的有无以及来波方向进行判定。空间谱估计的相关算法[1,2,3]可以很好的完成该任务，例如经典的Copon、MUSIC以及其他子空间类的各种算法。对于一维DOA估计方法而言，其仅能够完成一个维度的来波方向估计。而二维DOA估计方法，可以实现对空间电磁波的俯仰角和方位角信息的同步获取。

在DOA算法中，MUSIC算法突破了瑞利极限，可以实现超分辨估计[4]。二维 MUSIC算法是二维DOA估计的典型算法，此方法可以产生渐近无偏估计，但要在二维参数空间搜索谱峰，其计算复杂度大，而且空间谱峰搜索十分耗时。基于经典二维MUSIC算法的上述缺点，下面给出一种基于降维处理的MUSIC算法。

1　信号模型

一个M×N的矩形阵，其相邻阵元间距为d 。假定信号满足远场条件，噪声与信号独立，且是加性独立分布的高斯过程。假设有K 个非相干信源，第k 个信源对应的仰角和方位角分别为θk和φk，与x轴和y轴的夹角分别为αk和βk，角度关系如图1所示。

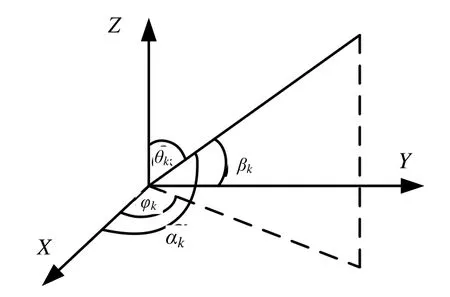
图1　角度关系

根据图1的角度关系，可得如下几何关系：

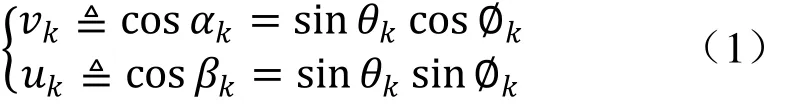
上半球面内有，θk∈ [0～90°],∅k∈ [0～360°],αk∈[0～180°],βk∈ [0～180°]，这里 ≜表示定义。

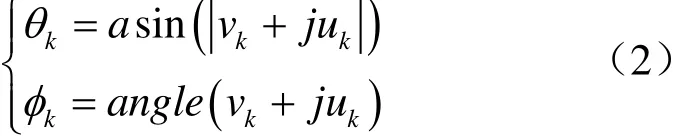
2　算法描述

2.1　二维MUSIC算法

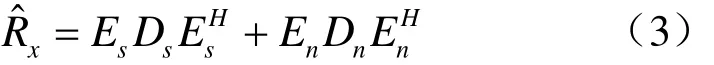
其中，Ds表示由K 个最大特征值组成的K×K的对角矩阵，而Dn表示由余下的MN-K个小特征值组成的对角矩阵。Es由K 个最大特征值对应的特征向量组成，而En由余下MN-K个最小特征值对应的特征向量组成。Es和En可以分别认为是信号子空间和噪声子空间。

二维MUSIC空间谱函数为[5]

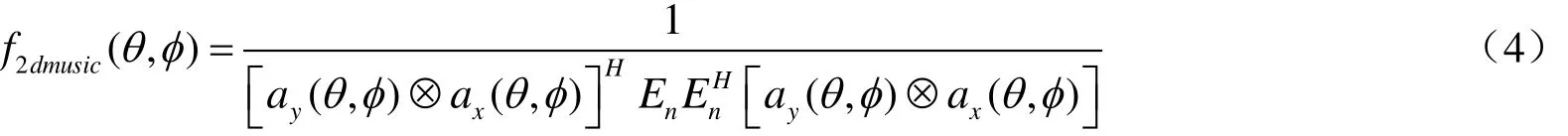
其中，⊗表示Kronecker积；

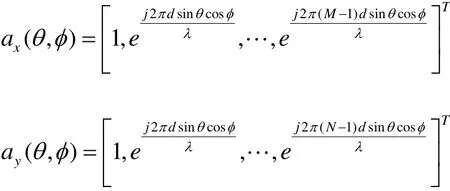
由于二维MUSIC需要二维搜索，其计算复杂度高。下面，给出一种只需要进行一维局部搜索的降维算法进行二维DOA估计。

2.2　MUSIC算法的降维处理

定义

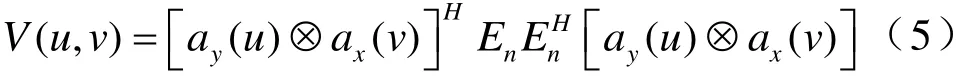
式（5）也可以表示为：

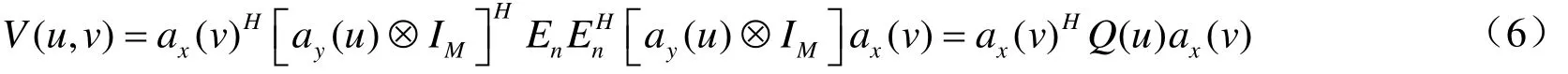
构造下面的代价函数

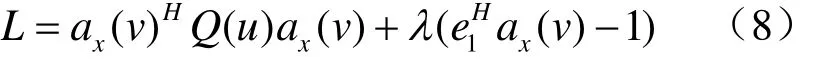
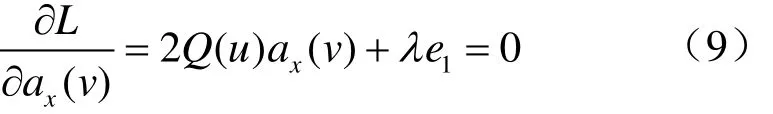
根据式（9）得

代入式（10）得

将式（12）代入式（7）中的目标函数可得

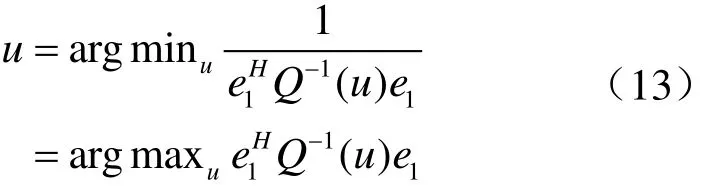
下面进一步求解α角。

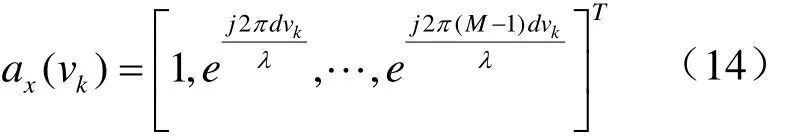
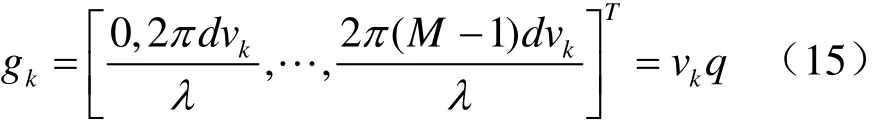
3　仿真分析

为了验证该算法性能，采用 1000次 Monte Carlo仿真来评估算法的角度估计性能。定义均方根误差（RMSE）为

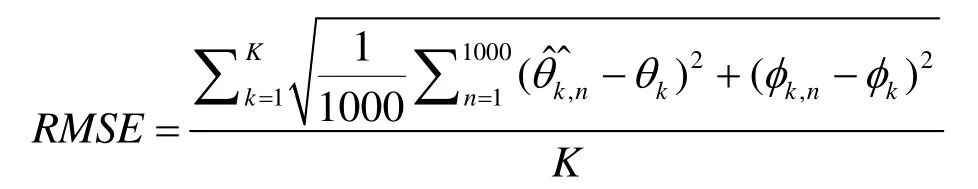
下面是相关性能仿真结果，图2为二维MUSIC谱扫描的等高线图；图3为信噪比SNR为10dB时的降维MUSIC的角度估计性能；图4是快拍为100时，降维MUSIC算法的RMSE随SNR的变化曲线；图5是SNR为10dB时，降维MUSIC算法的RMSE随快拍数变化曲线。

基于降维处理的MUSIC算法只需进行一次一维全局搜索和K次最小二乘估计，即可获得相互配对的俯仰角和方位角的估计值，避免了二维MUSIC算法进行二维全局搜索极其耗时的缺点。

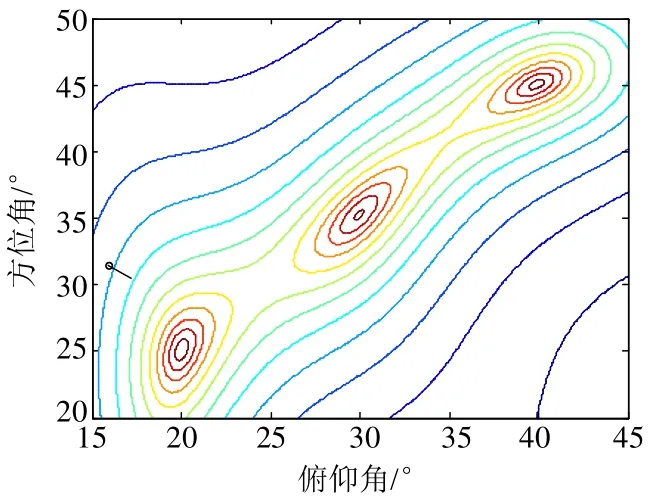
图2　二维MUSIC谱估计等高线图

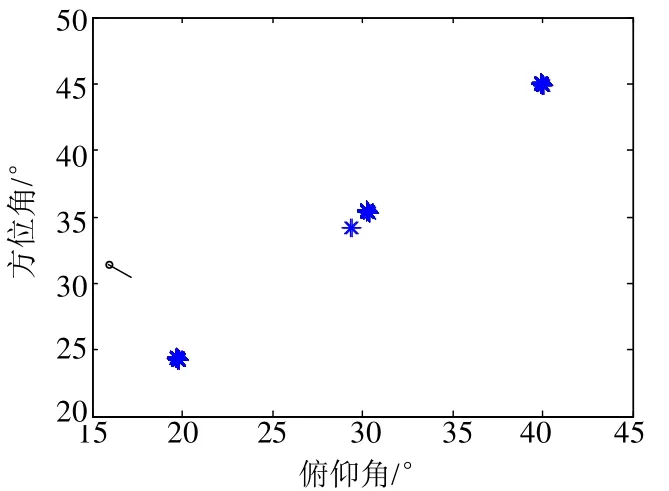
图3　SNR=10dB时的角度估计性能

图4　RMSE随SNR的变化曲线

该算法进行了1000次Monte Carlo仿真，从角度估计误差的仿真结果可以看出，基于降维处理的MUSIC算法与经典二维MUSIC算法性能接近。同时给出了降维MUSIC算法的角度估计误差曲线随SNR和快拍数的变化关系，可看出角度估计误差随SNR和快拍数的增大而减小。

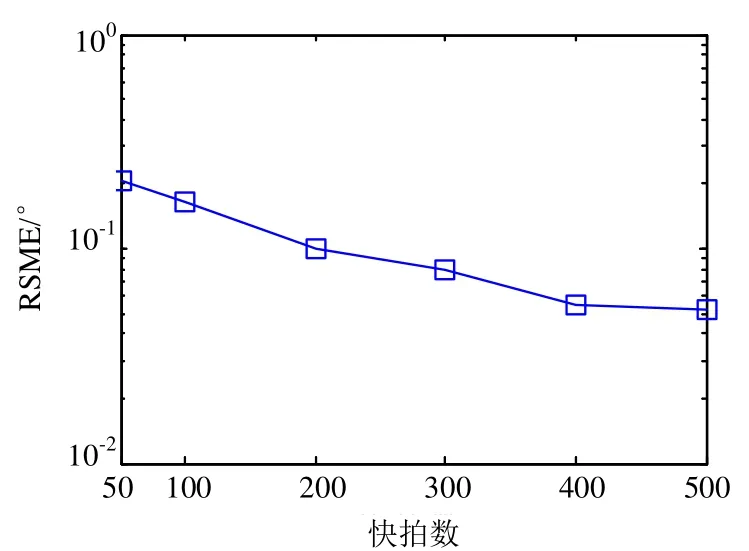
图5　RMSE随快拍数变化曲线

4　结论

该算法将二维 MUSIC处理转化为了一维MUSIC处理和最小二乘估计，实现了二维MUSIC算法的降维简化。该算法的复杂和搜索范围都大大降低，仿真表明其角度估计效果较好。