基于高次差法的降低北斗定位漂移研究
陈石平,廖丁毅,郑健超,林时君
(1 广州奥格智能科技有限公司,广州 510663;2 广州海格通信集团股份有限公司,广州 510663;3 湖南交通工程学院,衡阳 421219)
0 引言
目前卫星导航定位误差的来源有:与卫星有关的误差,传播路径误差、接收机与测站有关的误差,此外导航信号在地形复杂的环境比如高楼林立的城市中容易发生反射而产生多径效应或者导航信号被高楼遮挡无法传递到接收机,这些干扰会对接收机定位产生不利的影响,使得定位精度变低,产生“漂移现象”[1][2],具体理论分析见参考文献[3]。此外不同的时间、地点、气候等都会影响定位模块的定位精度,所有厂商的卫星定位模块都不可避免发生“漂移现象”,在出现严重漂移的情况下,对于车载应用会造成如超速警告、超区域行驶警告、监控目标消失或者移动目标的轨迹紊乱等误判,影响了使用效果,降低了可信度。
降低定位漂移:一方面是使用高成本的方案(螺旋或扼流圈天线+高精度板卡方案),通过通用分组无线服务技术(general packet radio service,GPRS)是或者电台获得电离层等改正信息后得到厘米级、亚米级的定位精度,如载波相位差分(real-time kinematic,RTK)、实时动态码相位差分(real-time differential,RTD)等高精度产品;另一方面后端处理主要通过某种算法进行后续处理[3],校正定位精度或者是剔除定位奇异(漂移)点,如导航仪地图软件进行定位数据核查、校正以及锁路功能,保证移动物体沿着正确的道路行进,一旦出现漂移可以通过校正算法强行将定位数据移到行进线路上,保证导航的准确性,因此在地图软件上定位轨迹表现比较好。然而RTK、RTD成本高,考虑到硬件成本因素,北斗车载终端一般不使用高精度板卡或地图软件,因此难以用差分方式或者地图软件(锁路)等对定位数据的检查和校正,目前降低北斗的定位漂移进行相关研究主要如下:
欧式几何空间距离法[4]:以欧氏空间的距离作为是否漂移的衡量标准:计算两次传回的偏离度是否在规定的范围,若超过认为存在漂移现象,或者是通过设置速度最大、最小阈值,1s内若超过此阈值范围则属漂移直接丢弃该点。
时间序列法[3]:需要采集n(n≥50)个样本数据,分别对经度、纬度进行计算:计算该样本的k(1≤k≤n-1)阶自相关系数,形成自相关系数序列,然后施加对数变换和差分变换,又形成新的时间序列,如经度(纬度)的自相关系数在收敛在置信区间内,表明移动目标在经度(纬度)方向上定位数据正常,是一个平稳过程,即在经、纬度方向上没有出现明显漂移。
相关系数法[5]:获取经、纬度 n(n≥0)样本数据,对经、纬度样本分别计算1次差得到新的经、纬度序列,用归一化的互相关系数函数对新的经、纬度序列进行计算,得到归一化互相关系数曲线图,根据相关的程度进行判断,如曲线图顶部变化缓慢(主峰与侧峰相差很小),曲线两边对称,证明原序列是稳定的,定位是稳定的;如曲线图出现阶跃(如主峰与最大侧峰相差较大),证明序列是不稳定的,定位不稳定,出现了定位漂移,阶跃越大,定位漂移越厉害。归一化互相关系数曲线图的阶跃数量等于漂移数量。
欧氏空间的距离阈值作为一个衡量标准,是一种简单可行的算法,但欧氏几何空间里的距离阈值使用起来主观性比较大,且不同车速、不同的行驶环境对应不同的阈值,否则容易造成误判。时间序列校正法具有相关理论支撑,不失为一种好的校正方法,但计算涉及平方、开平方、三角函数、对数等超越函数的复杂运算,计算量较大;互相关系数校正法需计算经、纬度的互相关系数,涉及浮点乘除法、开平方等超越函数的运算,计算量较大;本文尝试使用基于高次差法的降低北斗定位漂移,其涉及的运算只有加减除法,运算量非常简单,与上述几种方法相比,将极大地简化了运算复杂度和减少了计算量。
1 高次差的原理
定义:对于一个给定的数列{xn},把它的前后两项xn+1与xn的差xn+1-xn记为Δxn,得到一个新的数列{Δxn},数列Δxn称为为原数列{xn}的1次差数列,如果Δ2xn=Δxn+1-Δxn,则数列{Δ2xn}是{Δxn}的2次差数列依此类推,可得出数列{Δxn}的r次差数列Δrxn,其中n、r为正整数。如果某数列的r次差是一非零常数列,称此数列为r次等差数列[6],显然r次等差数列是r阶数列的特例。二差次或二差次以上数列的统称为高次差数列。
高次差是对时间序列进行多次差分,其计算只涉及加减法,计算复杂度低,且具有抗粗差的能力,在数据粗差的剔除应用中,都取得了良好的效果。
在载波相位 RTK高精度定位中,在载波相位观测期间,由于其它物体等的遮挡、电离层电子的剧烈运动、卫星仰角低、存在多路径效应以及接收机本机震荡的不稳定或软件故障等原因,会导致信号失锁,并可能引起整周计数跳变,产生周跳,周跳的探测与修复必须在载波相位模糊度固定前进行,是精密定位相位观测资料处理的一项重要内容。1985年 Remondi首次提出用差分法进行周跳探测和修复[7],对相位原始观测序列历元间高次差,如果没有周跳,其高次差表现为偶然误差特性:围绕“0”附近变化的随机序列(不考虑误差影响);如果周跳发生[8],则会破坏这种规律性,在周跳历元高次差发生突变且邻近历元数值上满足一定的比例关系,确定周跳发生的位置和大小,完成探测较大的周跳和修复。
对于北斗定位模块输出速度v(≥0)、方位角等信息,输出频率一般为1Hz,因此以1s为间隔进行采集数据,得到速度序列Vn(n为自然数),1次差速度数列为ΔVn=Vn+1-Vn,对应 1s内的加速度(是描述速度变化快慢的物理量,由速度的变化量和时间决定);2次差速度数列为Δ2Vn=ΔVn+1-Δ Vn,对应 1s内的加加速度(又称急动度,描述加速度变化快慢的物理量,由加速度的变化量和时间决定),对于一般的应用而已很少涉及急动度;r次差速度数列为ΔrVn=Δr-1Vn+1-Δr-1Vn。
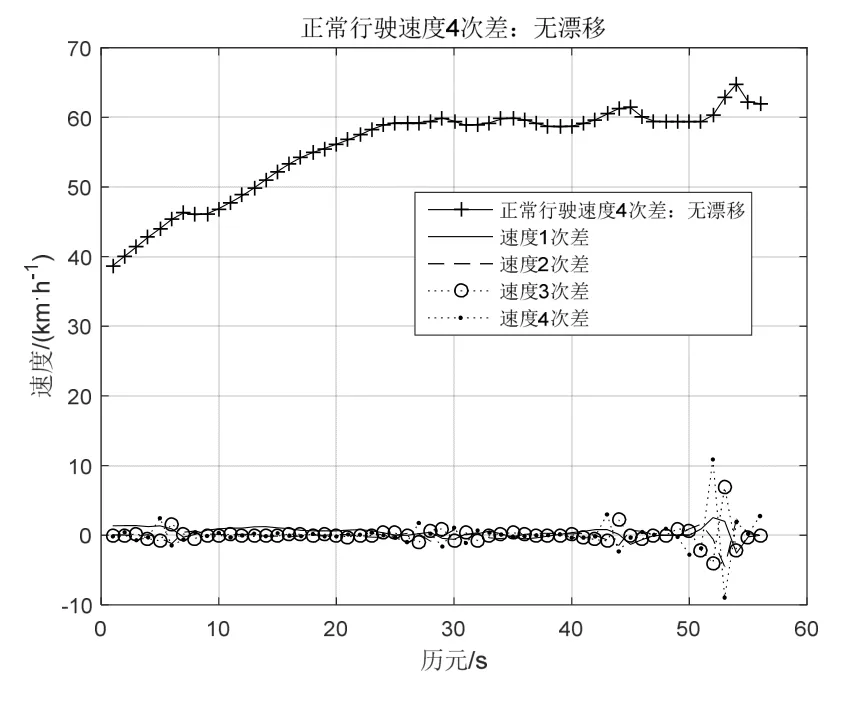
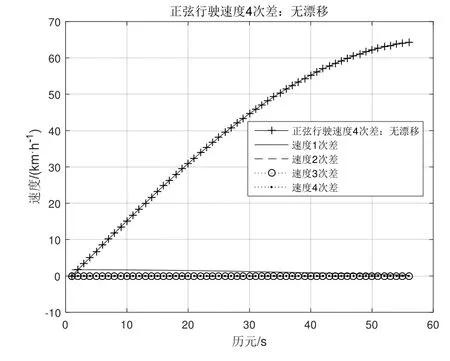
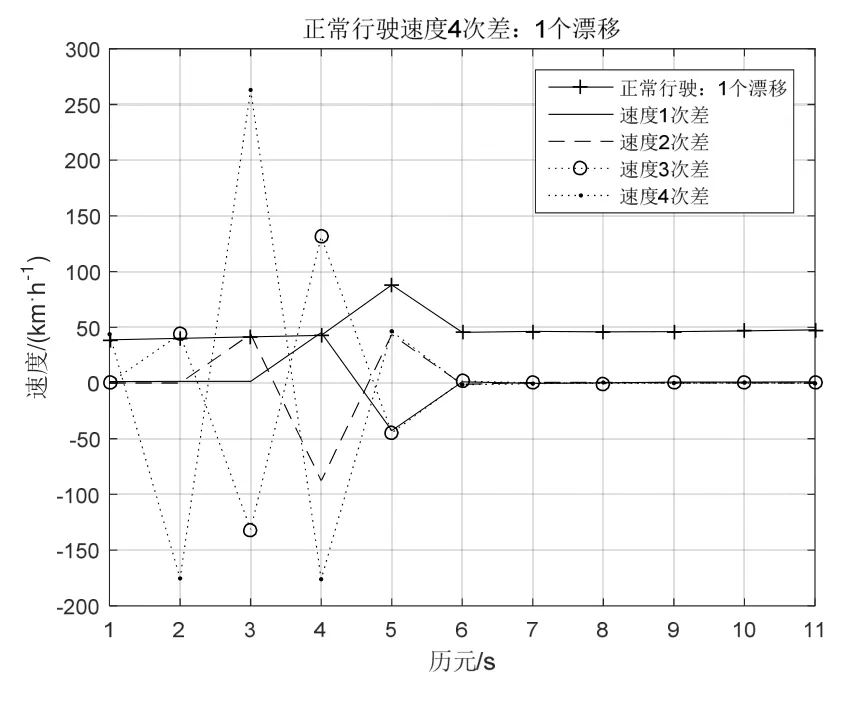
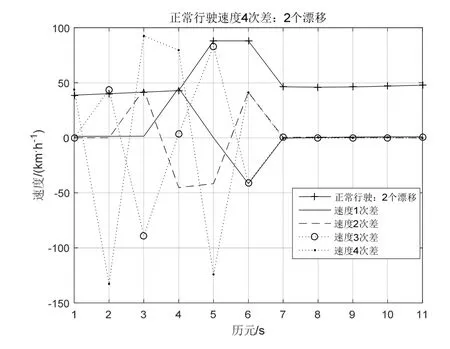
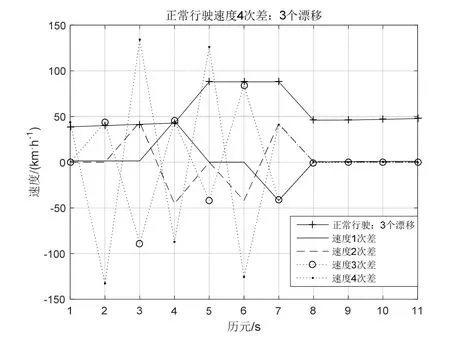
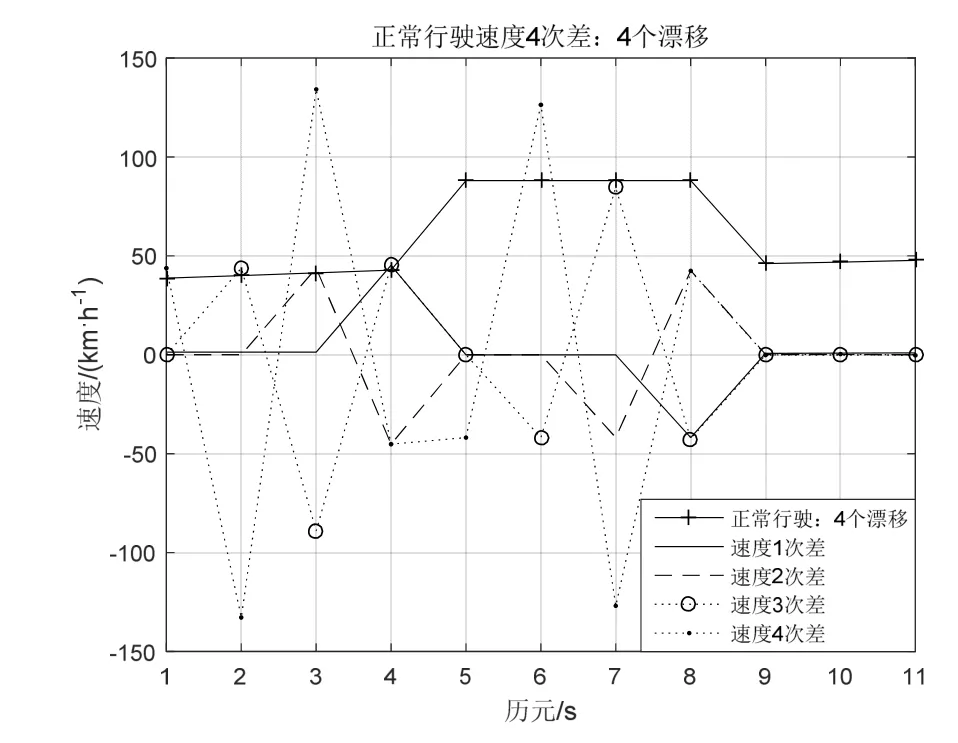
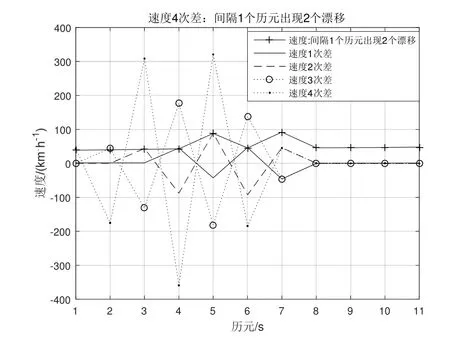
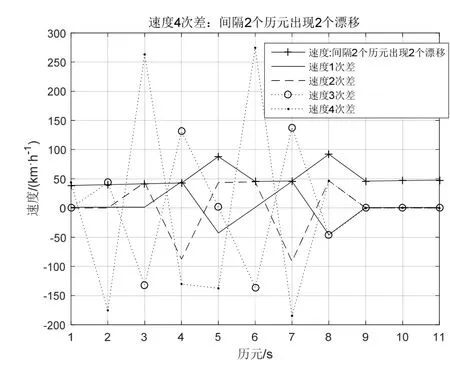
由物理学可以知,对于匀速运动1次差速度Δ Vn=0,对于匀加速运动2次差速度Δ2Vn=0。一般来说实际的速度时刻在变,存在 1次差ΔVi≠0,2次差Δ2Vj≠0(对于非匀加速运动有Δ2Vn≠0),其中自然数 i、j 对比周跳和漂移,两者存在很多相似之处,如两者产生的后果都会降低定位精度性能,基于此,本文提出利用速度4次差作为降低北斗定位漂移的一种算法。 在实际定位过程中,由于接收机内外的因素,经常引起卫星跟踪的暂时中断,漂移的发生往往存在连续性,产生漂移使得定位精度变低,因此有必要对多历元发生漂移的情况进行研究与分析。漂移探测的基本思路[2][9]∶以定位模块输出的速度为基础,通过计算不同历元间的速度高次差,组成一个关于时间的特征序列,通过判断特征序列尽可能地消除与时间有关的序列。如果没有发生漂移,特征序列随时间的变化应是平稳的;如果发生漂移这个平滑的序列就发生剧烈的跳变,探测检测量的变化是否符合评定指标,进而确定周跳发生的位置和大小。 假设历元 5发生单个漂移,速度为 V5+V,历元5和历元6发生连续2个漂移,速度分别为V5+V、V6+U,历元5至历元7发生连续3个漂移,速度分别为V5+V、V6+U、V7+Y,历元5至历元8发生连续4个漂移速度,分别为V5+V、V6+U、V7+Y、V8+Z。在4次差速度运算过程中[10],若不考虑Vn之间的计算(如匀速运动),只考虑其漂移速度,那么连续1~4个漂移的4次差速度的特征序列如下表[2][9][10]所示,特征序列具有偶函数性质。此外由概率可知,漂移次数越多其出现的概率越小,连续4次以上的漂移其概率很小,可认为难于出现。 表1 4次差速度特征序列(1~4个漂移) 表1对于匀速运动速度恒定,有Vn=V0,理论上1次差速度ΔVn=0,若在i时产生了单个漂移,速度为Vi=V+V0,则1次差速度ΔVi-1=Vi-Vi-1=V,Δ Vi=Vi+1-Vi=-V,1次差速度中产生2个阶跃(1正1负,和为 0),其余速度数列为零。2次差速度:Δ2Vi-2=ΔVi-1-ΔVi-2=V,Δ2Vi-1=ΔVi-ΔVi-1=-2V,Δ2Vi=ΔVi+1-ΔVi=V,2次差中产生3个阶跃(2正1负,和为0),其余速度数列为零。3次差速度:Δ3Vi-3=Δ2Vi-2-Δ2Vi-3=V,Δ3Vi-2=Δ2Vi-1-Δ2Vi-2=-3V,Δ3Vi-1=Δ2Vi-Δ2Vi-1=3V,Δ2Vi=Δ2Vi+1-Δ2Vi=-V,3次差中产生4个阶跃(2正2负,和为0),其余速度数列为零。4次差速度:Δ4Vi-4=Δ3Vi-3-Δ3Vi-4=V,Δ4Vi-3=Δ3Vi-2-Δ3Vi-3=-4V,Δ4Vi-2=Δ3Vi-1-Δ3Vi-2=6V,Δ4Vi-1=Δ3Vi-Δ3Vi-1=-4V,Δ4Vi=Δ3Vi+1-Δ3Vi=V,4次差中产生5个阶跃(3正2负,和为0),其余速度数列为零。依此类推,r次差产生r+1个速度阶跃。 对于匀速运动其速度恒定为V0:当定位漂移发生单个漂移时就产生突变而严重破坏这种规律性,4次差速度可以产生6倍漂移速度6V,相当于放大作用,若V=V0/6,4次差可达V0,若V=V0,4次差可达 6V0,随着漂移速度的增加,4次差变化更加明显。根据这种特性就可以把定位漂移探测出来。使用高次差法来探测和修复这些定位漂移,即对原始观测值在相邻的两个速度观测值间依次求4次差,于是就得到4次差,其中有漂移时刻的观测值会呈现很大的变化。 图1 正常行驶速度4次差 图2 正弦行驶速度4次差 在匀速运动若漂移速率均相等,即V=U=Y=Z,那么连续1至4个漂移4次差速度最大值分别为:6V、3V、3V、3V,其比值分别为 1∶-4∶6∶-4∶1、1∶-3∶2∶2-3∶1、1∶-3∶3∶-2∶3∶-3∶1、1∶-3∶3∶-1∶-1∶3∶-3∶1。当然实际运行过程中不可能一直为匀速运动,但在正常的运行过程中一般速率变化很小,可近似为匀速运动,当发生漂移时4次差速度大致遵循上述比例。 运动无漂移时,通过对各种速度曲线如正常行驶、正弦速度、匀速运动、匀加速运动等进行测试(速度最大值相同),其4次差变化很小,可认为在“0”附近随机变化的序列,正常行驶(2015年 2月6日广州天河区的定位数据)、正弦速度4次差如图1和图2所示。 图1正常行驶过程中若分别连续出现1至4个漂移,出现的为历元5至历元8,假设V=U=Y=Z=V5,连续出现1至4个漂移的4次差分别如图3~图6所示,图中只显示前面11个特征序列。 图3 正常行驶出现单个漂移 通过计算:单个漂移 4次差速度比值为43.78∶-175.40∶262.99∶-176.13∶46.40(1∶-4.006∶6.007∶-4.023∶1.060)近似于 1∶-4∶6∶-4∶1;连续出现两个漂移 4 次差速度比值为 43.78∶-132.77∶92.48∶79.64∶-124.17∶41.17(1∶-3.033∶2.112∶1.819∶-2.835∶0.940)近似于 1∶-3∶2∶2-3∶1;连续出现 3 个漂移 4 次差速度比值为 43.78∶-132.77∶1.34∶-87.19∶126.13∶-125.66∶41.08(1∶-3.032∶3.065∶-1.99∶2.881∶-2.870∶0.938)近似于1∶-3∶3∶-2∶3∶-3∶1;连续出现 4 个漂移 4 次差速度比值为 43.77∶-132.77∶134.18∶-45.19∶-41.86∶126.33∶-126.92∶42.48 ( 1∶-3.032∶3.065∶-1.032∶-0.956∶2.886∶-2.899∶0.969)近似于 1∶-3∶3∶-1∶-1∶3∶-3∶1。基本满足上述比例关系。从中可以发现若出现漂移,由此可以推断,对于速度较为平稳的运动,在发生连续漂移的情况下高次差法完全可以将漂移探测出来。 图1正常行驶过程中,若间隔1个历元出现2个漂移,4 次差速度特征序列为 V∶-4V∶7V∶-8V∶7V∶-4V∶V,出现的历元 5、历元 7,假设 2个漂移V=U=V5,出现1个漂移的4次差如图7所示,只显示前面 11个特征序列,4次差速度比值为43.77∶-175.40∶309.32∶-361.45∶324.39∶-186.78∶45.70(1∶-4.01∶7.07∶-8.26∶7.41∶-4.27∶1.044),其比值近似于特征序列比值。 图1正常行驶过程中,若间隔2个历元出现2个漂移,4 次差速度特征序列为 V∶-4V∶6V∶-3V∶-3V∶6V∶-3V∶V,出现的历元 5、历元 8,假设 2个漂移V=U=V5,连续出现1至4个漂移的4次差如图8所示,图中只显示前面11个特征序列,4次差速度比值为 43.77∶-175.40∶263.00∶-130.14∶-137.57∶274.51∶-184.61∶46.41 ( 1∶-4.006∶6.008∶-2.973∶-3.143∶6.271∶-4.217∶1.060),其比值近似于特征序列比值。 图4 正常行驶连续出现2个漂移 图5 正常行驶连续出现3个漂移 图6 正常行驶连续出现4个漂移 图7 间隔1个历元出现2个漂移 图8 间隔2个历元出现2个漂移 若间隔3个历元出现2个漂移,4次差速度特征序列为 V∶-4V∶6V∶-4V∶-2V∶-4V∶6V∶-4V∶ V。若间隔 4个历元出现 2个漂移,其 4次差特征序列为V∶-4V∶6V∶-4V∶V∶V∶-4V∶6V∶-4V∶1V,相当于单个漂移 4次差速度出现两次,从4次差计算过程也可以发现第5项与第6项之间没有关系,要不然只能求解五次以上的高次差,因此间隔4个历元的漂移其4次差可以认为是相互独立的,可以分开计算。此外间隔历元的漂移的组合有很多种情况,本文只是列举常见的几种情况,通过高次差法得到的比值基本满足上述特征序列比例关系,从中可以发现若间隔历元出现漂移也可以用高次差法可以将漂移探测出来。 定位漂移数据处理,对于被断定是漂移的定位数据,可以使用3种处理方法进行平滑[3]:直接删除该点定位数据;直接沿用前后两个有效的定位坐标值的平均值;利用前面几个有速度和方向角计算当前这个点的理论定位数据。 本文结合定位漂移现象出现的原因,结合自相关函数特性,提出一种基于高次差法判断定位漂移,对其算法进行介绍、分析和推导,该算法具有相关的理论基础,并通过试验测试,结果表明:可用速度的高次差法能有效地探测连续几个定位漂移或者是间隔历元漂移,并判断出现漂移的位置,并对定位漂移数据进行处理,并同时进行修正,进而提高定位可靠性和准确性,与文献5相比其方法具有更加简单的运算复杂度,两者相同的效果。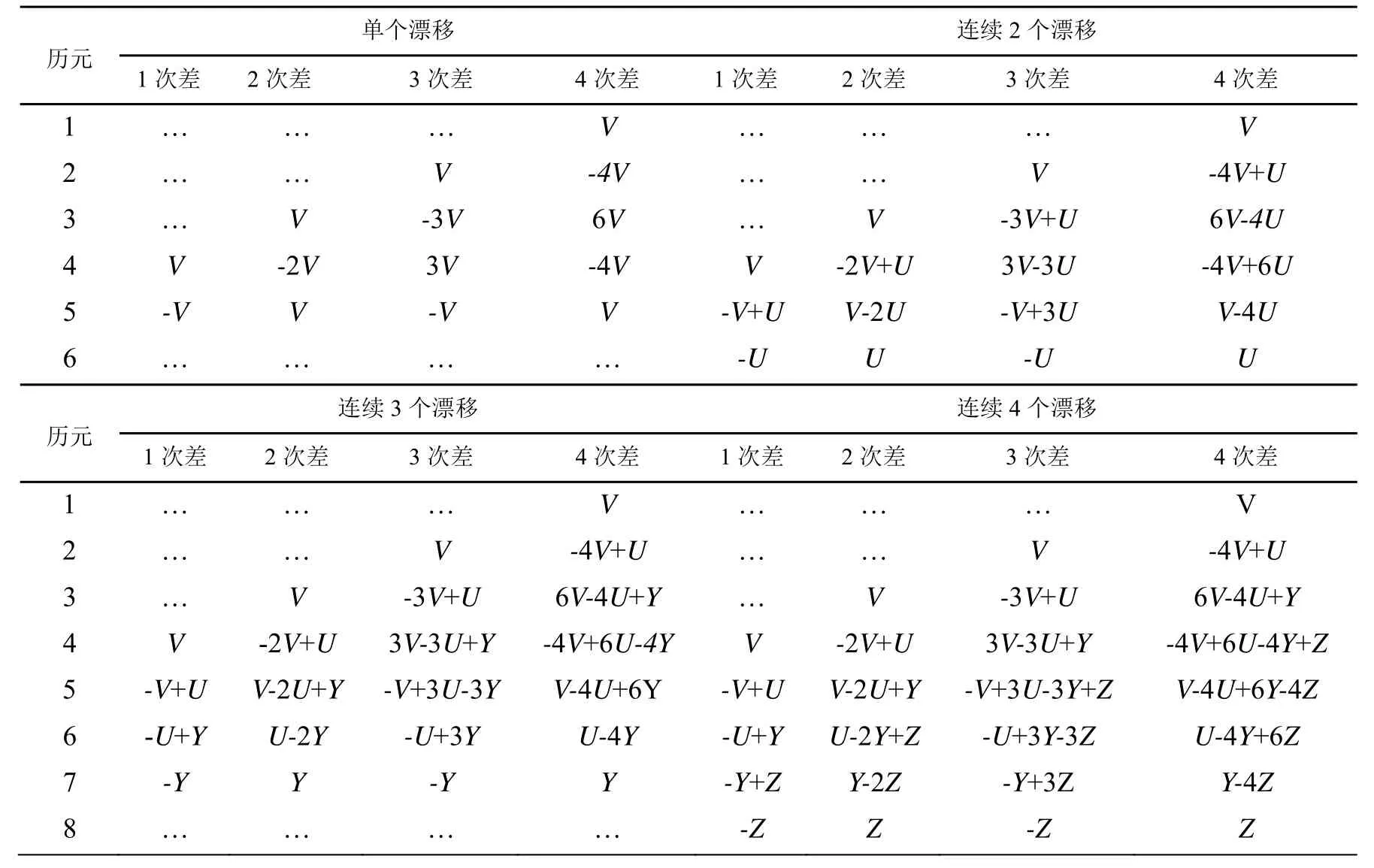
2 试验分析
2.1 连续漂移
2.2 间隔历元的漂移
3 结束语

