非线性多智能体系统的分布式编队控制

连文瑜 ，刘 佳 ，张运喜 ，李伟勋

（1.天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津 300222；2.天津职业技术师范大学自动化与电气工程学院，天津 300222；3.天津职业技术师范大学理学院，天津 300222）

随着科学技术的发展和通讯技术的应用，多智能体系统的一致性在许多研究领域受到广泛关注，如编队控制、分布式计算和机器人系统等[1-3]。多智能系统是多个智能体的组合，它们通过相互间的合作协商来完成单个智能体不能完成的任务，多智能体系统的一致性即设计适合的控制协议使各个智能体达到相同的状态。多智能体系统的编队控制与一致性问题有着密切关系，在编队控制时，智能体之间不仅要满足某些状态量使之达到一致，还需要和原来预先给定的队形保持一致。有许多学者对多智能体系的编队控制问题进行了研究，研究方法主要有基于领导-跟随的方法[4]，基于行为的方法[5]，基于虚拟结构式的方法[6]。文献[7]针对一阶多智能体系统，基于一致性方法来研究多智能体系统分布式编队控制。文献[8]针对一阶系统设计控制协议，研究了离散多智能体系统在固定有向拓扑结构中的分布式编队控制。在考虑二阶多智能体系统时，与一阶多智能体系统有所不同，单个智能体的动力学模型不仅与位置有关，还与速度有关。文献[9]研究二阶动力系统的一致性问题，提出简单的二阶一致性协议，实现了多智能体系统的编队控制。文献[10]实现了二阶多智能体系统的环形编队控制研究。文献[11]研究了多智能体的自适应算法。但在实际的应用过程中，多智能体系统具有非线性动力学特性[12-13]，因此，研究非线性多智能体系统的编队控制十分必要。文献[14]对含有非线性特性的二阶多智能体系统，给出了一致性控制的研究。本文基于一致性协议，研究二阶多智能体系统的编队控制问题。

1 分析工具

1.1 图论知识

代数图论为重要的研究工具，将多智能体系统中的每个智能体看作一个质点，它们之间的关系可以用图论的方式描述。

令 G（Q，E，A）为有向图，其中 Q={q1，q2，…，qn}表示n个节点的集合，E∈Q×Q表示有向边的集合，A表示邻接矩阵。记eij=（qi，qj）∈E为有向边，qi为边的父节点，qj为边的子节点，边的方向为由qi到qj。通常用邻接矩阵来描述各节点之间的关系，邻接矩阵为：

式中：如果第j个节点能接收到来自第i个节点的相关信息，则aij＞0，∀i≠j。aij为边（qi，qj）的权值。否则，aij=0，而对角线上的元素aii=0，则说明该有向图中不含有闭自环。在图中，节点qi的入度用degin（qi）表示，出度用degout（qi）表示。

图的Laplacian矩阵用另外一种方式描述了所对应的图的所有信息，定义如下：

式中：D为图G的入度矩阵，D=diag（degin（q1），degin（q2），degin（qn））；A为邻接矩阵。

1.2 相关数学工具

矩阵的Kronecker积是一种重要的矩阵乘积，在矩阵理论的研究中具有广泛应用，同时也是在研究控制系统理论时的重要数学工具。

定义 1[15]设 A=[aij]∈Rm×n，B=[bij]∈Rp×q，则分块矩阵

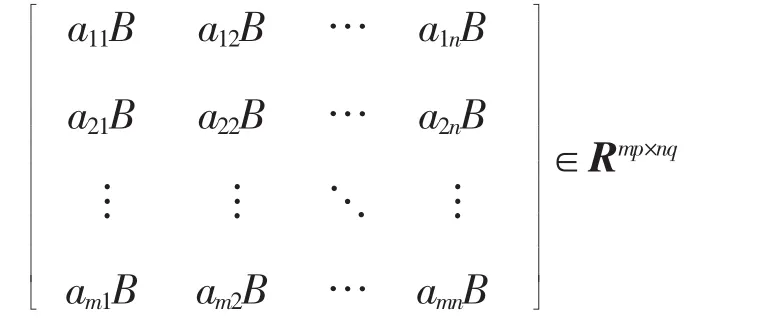
称为矩阵A与矩阵B的Kronecker积，记为A⊗B。

下面介绍本文用到的相关引理：

引理1[16]（Schur补引理）给定的对称矩阵S=以下2个条件为等价的：

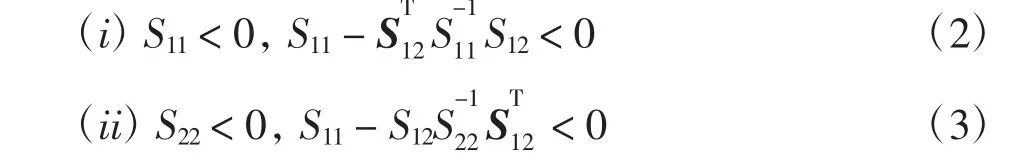
引理2[17]对于任意的常向量a，b∈Rn和正定矩阵Φ∈Rn×n，以下不等式成立：

2 问题描述与分析

2.1 系统描述

本文所研究的多智能体系统是由1个领导者和n个跟随者组成的。领导者用0来标记，跟随者用1，2，…，n来标记。

假设所考虑的跟随者智能体的动态模型为：

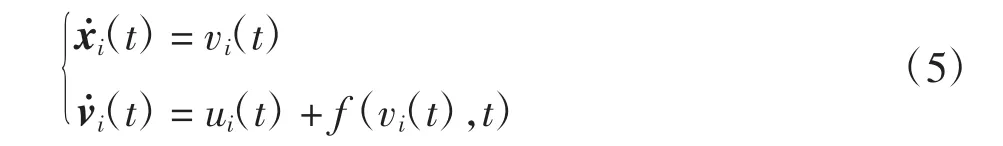
式中：xi（t）∈Rm为第i个智能体的位置向量；vi（t）∈Rm为速度向量；ui（t）∈Rm为控制输入；f：Rm×R→Rm为连续可微的函数向量。

领导者智能体的动态模型为：

式中：x0（t）∈Rm为领导者的位置向量；v0（t）∈Rm为速度向量。

假设1非线性动态f（vi（t），t）（i∈{0，1，2，…，n}）是连续可微的函数向量，存在非负常数ρ，对于任意的t≥0满足下列条件：

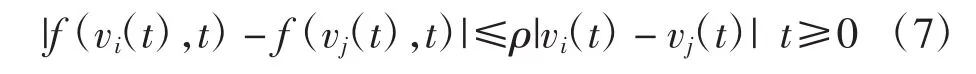
定义2为多智能体系统领导-跟随编队控制问题可解的定义。

定义2考虑所给出的多智能体系统，在任意的初始状态xi（0），vi（0）下，领导者和跟随者的位置和速度应该满足下列要求：

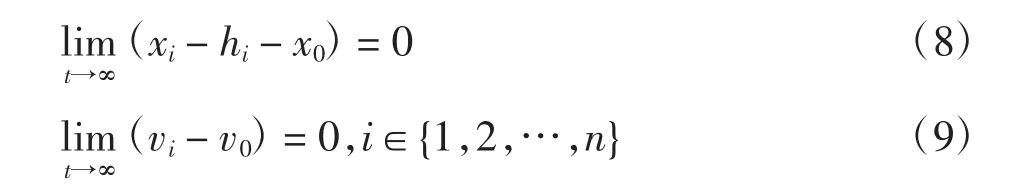
式中：hi∈Rm为第i个智能体与领导者之间期望的队形常向量。

根据所给出的多智能体系统，控制器设计如下：

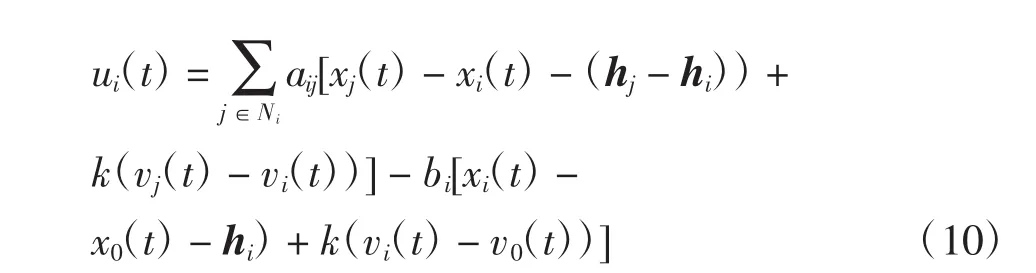
式中：Ni为第i个智能体在图G中的邻居集合；k＞0为速度增益；hi为第i个智能体与领导者之间期望的队形向量；hj为第j个智能体与领导者之间期望的队形向量；aij＞0为第i个智能体与第j个智能体的连接权值；bi为第i个智能体与领导者之间的连接权值，分别定义为：

将式（10）代入系统（5）中，得：

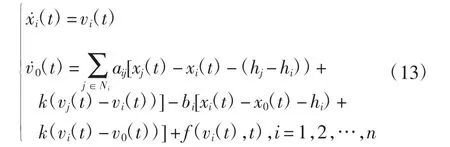
通过Kronecker积，可以把误差系统（14）转化为矩阵形式：

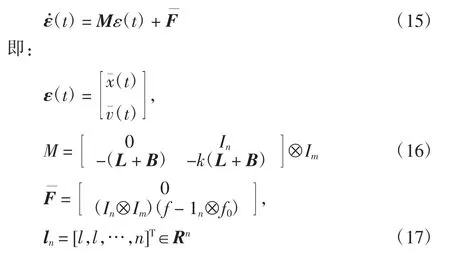
式中：L为图G的Laplacian矩阵；B为跟随者与领导者之间的连接矩阵，记作 L=diag（b1，b2，…，bn）。

2.2 主要结果

定理1针对具有非线性特性的多智能体系统，对于给定的正常数ρ，存在适当维数的正定矩阵P，R满足下列的线性矩阵不等式：

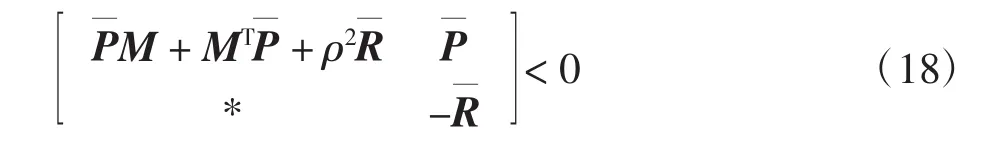
证明选取Lyapunov函数

对 V（t）沿着系统（15）求导，可得：

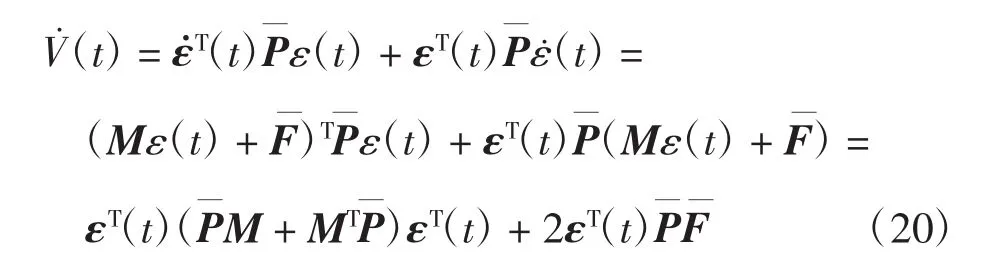
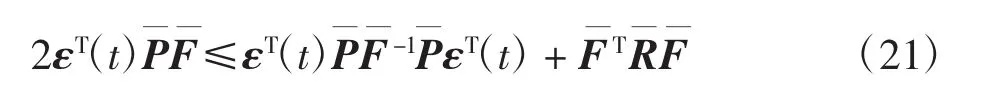
将式（21）代入式（20）中，可以得到：

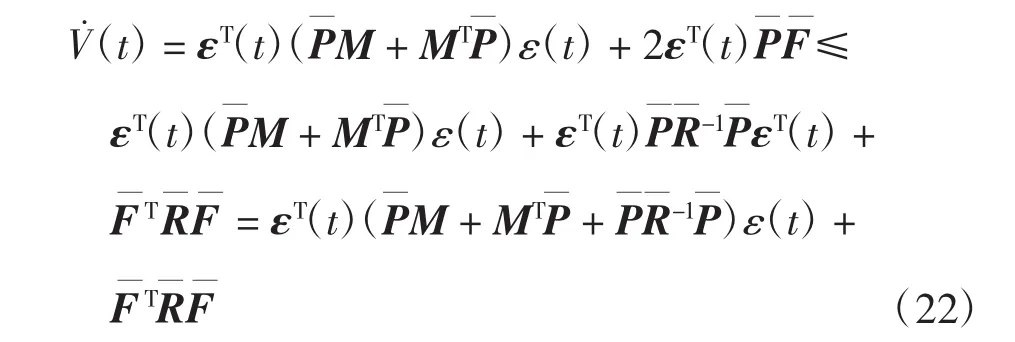
又由假设1可以得到：

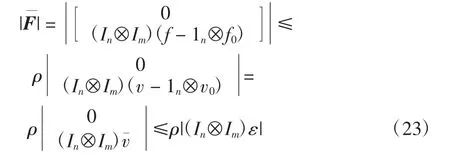
将式（23）代入式（22），可以得到：

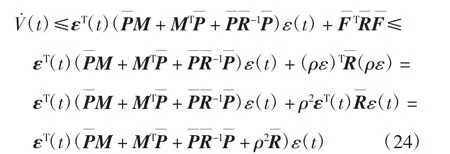
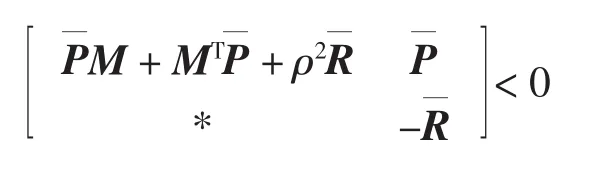
3 数值仿真

3.1 仿真例子

例1考虑该多智能体系统由4个跟随者与1个领导者智能体所组成，智能体之间的拓扑结构关系如图1所示。

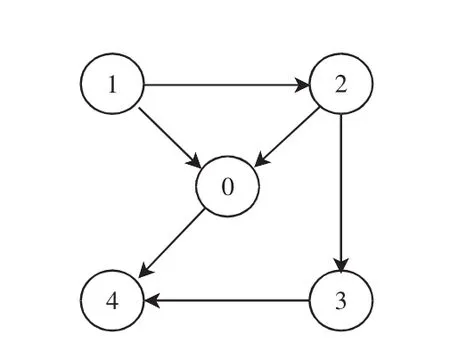
图1 智能体拓扑结构

假设智能体之间的连接权值为0或1，则跟随者之间所对应的Laplacian矩阵为：

跟随者与领导者之间的连接矩阵为：

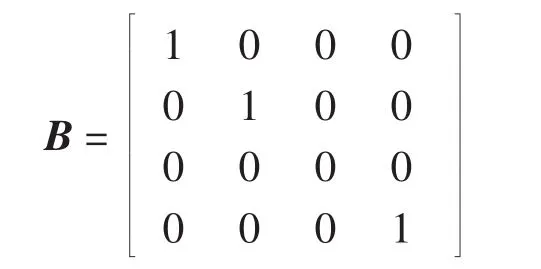
假设多智能体系统是在二维平面上的系统，且非线性动态为：

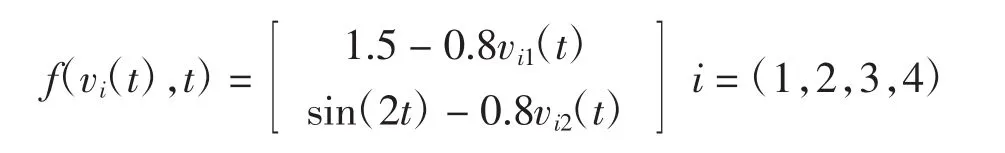
由假设1可得ρ=0.2，期望的队形向量分别为：

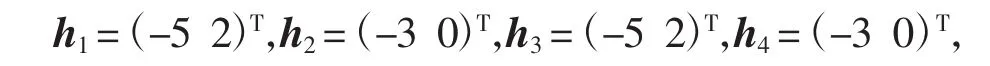
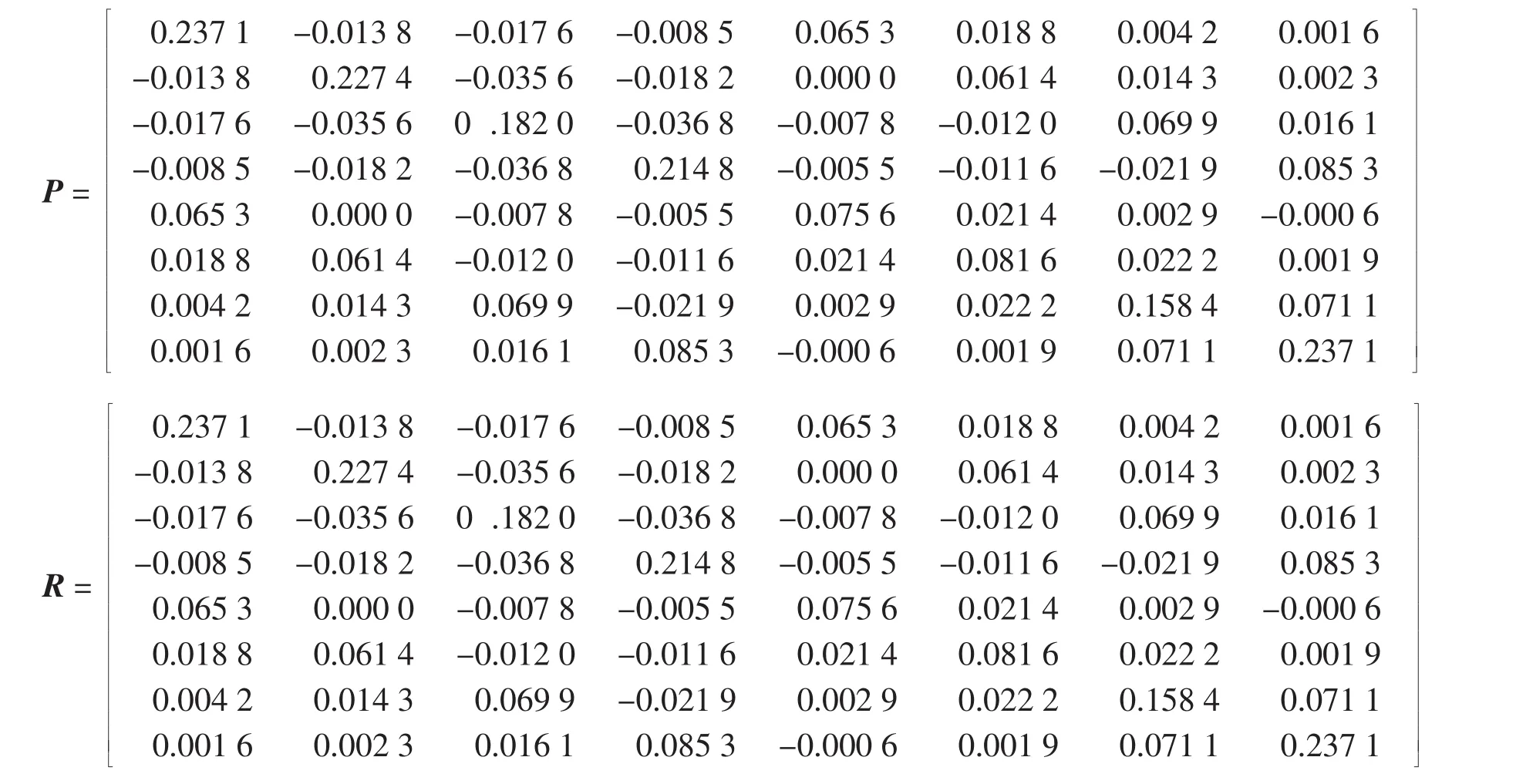
令k=2，通过Matlab中的LMI工具箱，可以求解定理1中的线性矩阵不等式（18），求得可行解为：

3.2 仿真结果

通过仿真图来描述多智能体的状态轨迹及位置误差和速度误差的变化趋势，智能体的状态轨迹如图2所示，位置误差状态轨迹如图3所示，智能位置误差状态轨迹如图4所示，速度误差状态轨迹如图5所示，智能体的速度误差状态轨迹如图6所示。

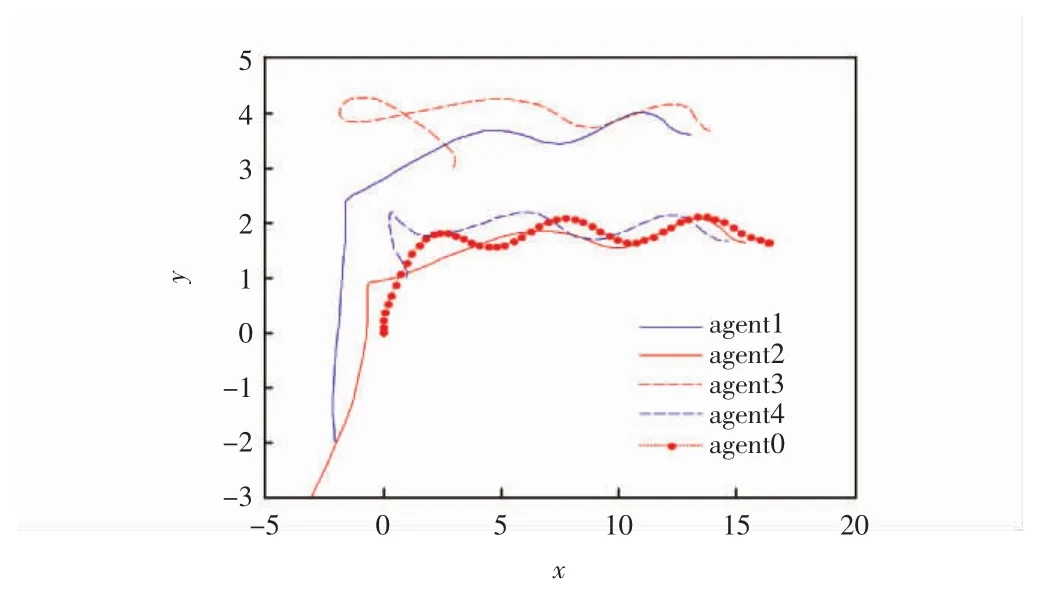
图2 智能体的状态轨迹

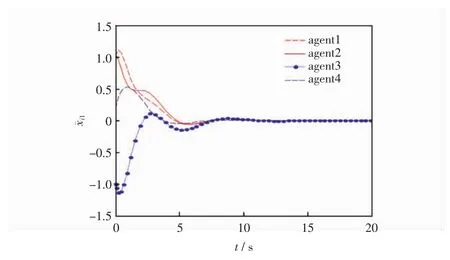
图3 智能体的位置误差i1状态轨迹

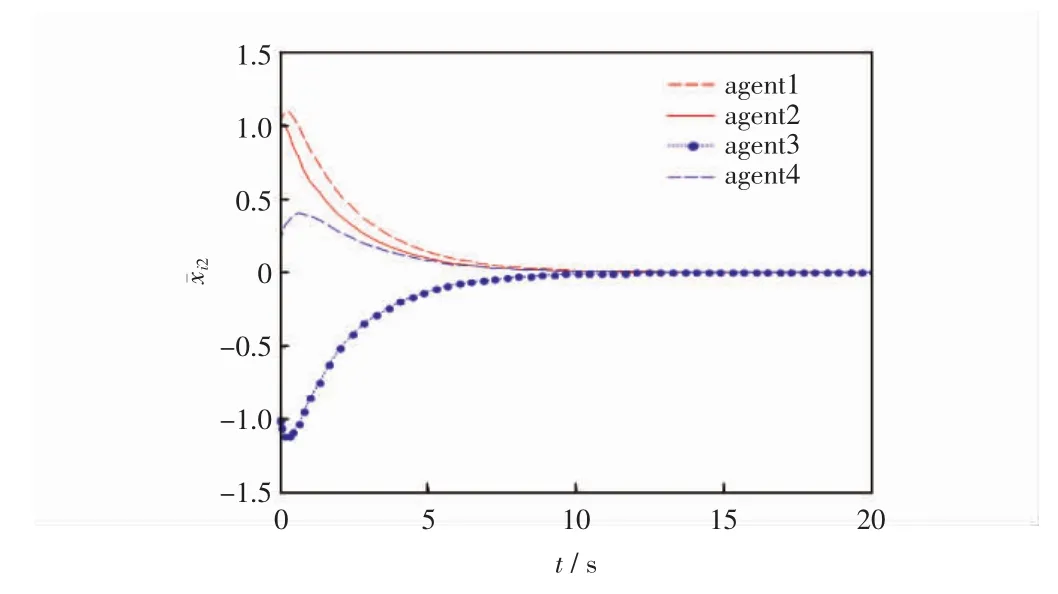
图4 智能体的位置误差¯i2状态轨迹

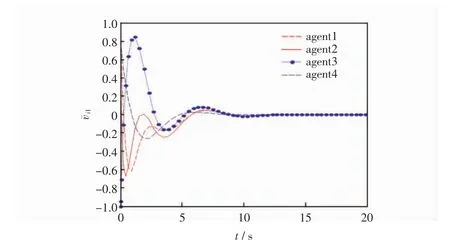
图5 智能体的速度误差¯i1状态轨迹

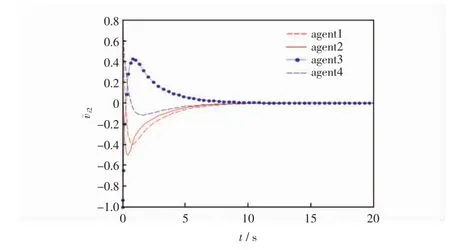
图6 智能体的速度误差¯i2状态轨迹

从图2中观察4个智能体与领导者的运动轨迹，可以发现智能体能够达到所期望的队形；从图3和图4这两个图中可以看出在二维平面下，多智能体系统的位置误差在随着时间的变化最终都会趋近于零，即跟随者与领导者的位置可以达到一致；从图5和图6可以看出在经过一段时间后，多智能体系统的速度误差会趋于零，即跟随者的速度可以满足领导者的速度，多智能体系统达到稳定的状态，也就是说多智能体系统既能够满足期望的队形，跟随者又能够与领导者的速度达到一致。因此，证明了所得理论的有效性。

4 结语

本文研究了二阶多智能体系统的编队控制，在具有非线性动态特性的情况下，设计了合适的分布式编队控制协议，利用Lyapunov稳定性理论和基于线性矩阵不等式的方法对控制协议进行稳定性分析，得出多智能体系统能够按照所期望的队形运动，而且位置误差和速度误差在经过一段时间后趋于零，达到稳定状态，通过数值仿真实例验证了所得结论的有效性，即多智能体系统不仅能够得到所期望的队形，而且跟随者的速度和领导者智能体的速度能够达到一致。