分数阶超混沌系统异构射影延迟同步研究

张宗瑶，赵小山，卢 雅，徐 涛

（天津职业技术师范大学理学院，天津 300222）

分数阶微积分理论的发展最早可以追溯到300多年前。分数阶微积分作为微积分的一个分支，是普通的整数阶微分和积分向任意实数阶微分和积分的推广。由于长期缺少实际应用背景，所以分数阶微积分理论的发展较为缓慢。但研究表明分数阶较整数阶混沌系统能够更好地将物理工程现象呈现出来，且分数阶模型较传统的整数阶模型有更为复杂的动力学特性，所以更适合描述真实材料的特性[1-2]。目前，混沌同步广泛应用在密码学、信息科学和图像处理等领域。混沌同步的研究既体现混沌自身应用价值也为混沌的应用研究提供了良好的理论基础[3]。

混沌同步在保密通信中的应用研究已成为非线性系统研究的一个热点，并且许多混沌同步和控制方法逐渐被提出，例如完全同步、自适应同步、脉冲同步、延迟同步和射影同步等同步方法和非线性反馈控制、线性反馈控制、滑模控制和模糊控制等控制方法。其中把驱动系统和响应系统的状态变量关于一个比例因子同步的方式定义为射影同步。由于比例因子增加了系统的随机性和不可测性，因此射影同步对于保密通信研究有更为突出的优势。目前有很多射影同步方法被提出，例如广义射影同步[4]、修正射影同步[5]、全状态混合射影同步[6]、错位射影同步[7]、函数射影同步[8-9]和延迟射影同步[10]等同步方法。由于延迟现象在非线性动力系统中是不可避免的因素，因此本文提出的射影延迟同步方案更加符合实际，也保留了射影同步在增强信息传递的安全性方面的优势。基于文献[3]，本文以线性分数阶稳定性定理[11]和非线性控制方法为理论基础，实现分数阶异构超混沌系统的射影延迟同步和未知参数辨识，设计控制器和参数辨识规则，并以Lorenz-Stenflo和Lorenz这2个超混沌系统为例进行数值仿真，证明所设计的控制器和参数辨识规则的有效性。

1 系统数学模型与问题描述

目前 Grnwald-Letnikov（G-L）、Riemann-Liouville（R-L）和Caputo这3种分数阶微积分的定义是多种分数阶微分和积分的数学定义中较为常见的3种。R-L定义多被采用于研究纯数学问题，而在实际应用中Caputo定义较为常用。因此，本文采用Caputo定义。

Caputo分数阶微分的定义为：

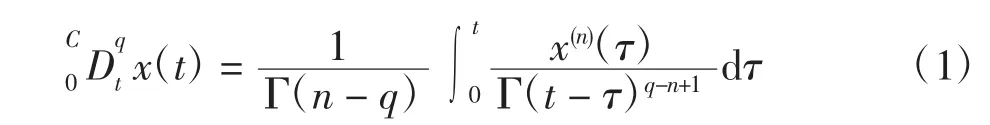
式中：n为大于q的最小整数；Γ（·）为伽马函数。

考虑如下的分数阶驱动系统：

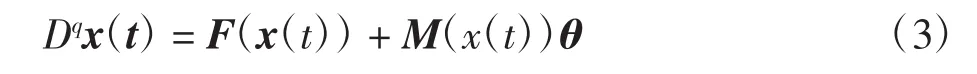
式中：x（t）=（x1（t），x2（t），…，xn（t））T∈Rn为驱动系统的状态变量向量；驱动系统的求导的分数阶阶数q∈（0，1）；向量函数 F：Rn→Rn为连续的；θ =（θ1，θ2，…，为驱动系统的未知参数向量且 M（x（t））∈为多项式矩阵。

考虑如下的分数阶响应系统：

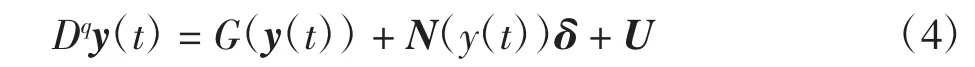
式中：y（t）=（y1（t），y2（t），…，yn（t））T∈Rn为响应系统状态变量向量；响应系统的求导的分数阶阶数q∈（0，1）；向量函数 G：Rn→Rn为连续的；δ=（δ1，δ2，…，为响应系统的未知参数向量且 N（y（t））∈为多项式矩阵；U=（u1，u2，…，un）T为待设计的非线性反馈控制器。

定义系统（3）和（4）间的状态变量误差为：

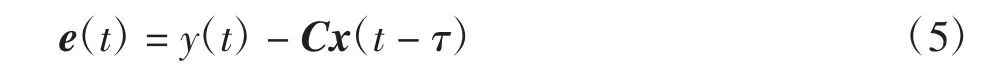
式中：e（t）=（e1（t），e2（t），…，en（t））T∈Rn；C=diag{c1，c2，…，cn}∈Rn×n为实比例矩阵；τ＞ 0 为同步时间延迟。

定义系统（3）和（4）未知参数的误差为：

定义1如果存在控制器U使得

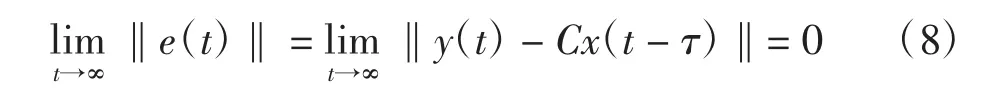
则称驱动系统（3）与响应系统（4）这两个异构分数阶混沌系统之间实现了射影延迟同步。

注：当 C=I，I∈Rn×n时，同步类型称为延迟同步，而当 C=-I，I∈Rn×n时，同步类型称为反相延迟同步；当延迟量τ为0时，同步类型由射影延迟同步退化为射影同步；当延迟量τ为0，且C=I或者C=-I时，同步类型分别转化为完全同步和反相同步，因此本文主要目的是设计合适的控制器实现系统（3）和系统（4）的射影延迟同步及合适的自适应参数辨识规则，以辨识出系统（3）和（4）的未知参数。

2 控制器和参数辨识规则的设计

设非线性控制器为：

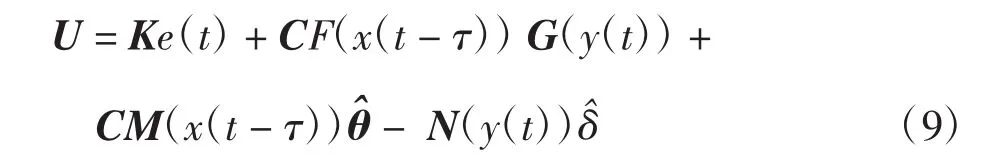
式中：反馈增益 K=diag{k1，k2，…，kn}∈Rn×n为待定对角矩阵。将新设计的控制器（9）作为响应系统（4）待设计的控制器，再根据射影延迟同步定义结合驱动系统（3）和响应系统（4）计算可得误差系统为：

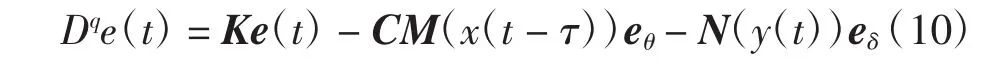
那么，最终将实现分数阶混沌系统（3）和（4）间的射影延迟同步问题和未知参数辨识问题等价转化成分数阶误差系统（10）零解的渐近稳定性问题。

定理 1如果矩阵 K=diag{k1，k2，…，kn}∈Rn×n满足 ki＜ 0，i=1，2，…，n，那么不确定分数阶混沌系统（3）与（4）就能够实现射影延迟同步，并且未知参数向量θ、δ能够由以下的参数更新规则识别为：

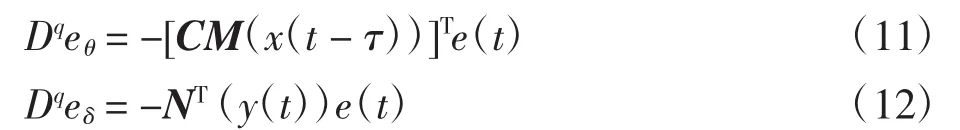
由同步误差系统（10）和参数更新规则（11）和（12）组成新的误差系统为：

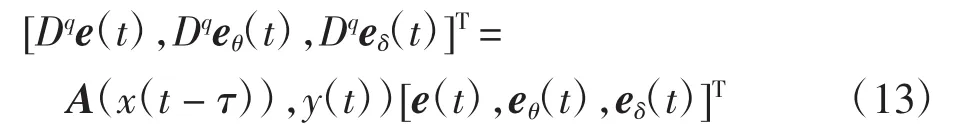
式中：A（x（t- τ）），y（t））为矩阵多项式。

引理1[3]如果分数阶线性自治误差系统（13）的系数矩阵 A 的所有特征值 λ 均满足|arg（λ）|＞ qπ/2，q∈（0，1）则称分数阶线性自治误差系统（13）的零解是渐进稳定的，即

证明假设误差系统中的多项式系数矩阵的任意一个特征值为λ，相应的非零特征向量为η，则

对上式左乘ηT可得：

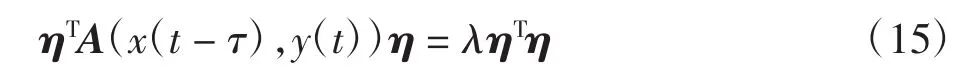
同理可得

由方程（16）和（17）计算可得：

式中：ηTη＞0；A（x（t-τ），y（t））+AT（x（t-τ），y（t）），即：

由矩阵 K=diag{k1，k2，…，kn}∈Rn×n满足 ki＜ 0（i=1，2，…，n）知，ηTQη≤0。那么

此时，多项式矩阵 A（x（t- τ），y（t）的任意 1 个特征值 λ 均满足|arg（λ）|≥π/2 ＞ qπ/2，其中 q∈（0，1）。根据引理1，分数阶系统（13）在零解是渐进稳定的。即从理论上证明了实现不确定分数阶混沌系统（3）和（4）间射影延迟同步的可能性，同时也说明了本文设计的辨识驱动系统（3）与响应系统（4）中的未知参数向量的参数辨识更新规则（11）和（12）的正确性。

3 数值仿真

为方便从数值上验证本文提出的射影延迟同步方案的可行性，以下面分数阶超混沌Lorenz-Stenflo系统和分数阶Lorenz超混沌系统这2个分数阶四维超混沌系统为实例进行数值仿真，其中整数阶超混沌Lorenz-Stenflo系统是由Stenflo在研究低频短波长的重力波方程式时提出的[12]，具体形式为：

其中，当系统（20）的参数向量取值为{a，b，c，d}={1，0.7，26，1.5}时存在混沌吸引子，即此时为混沌系统。

本文研究的是系统（20）的分数阶形式：

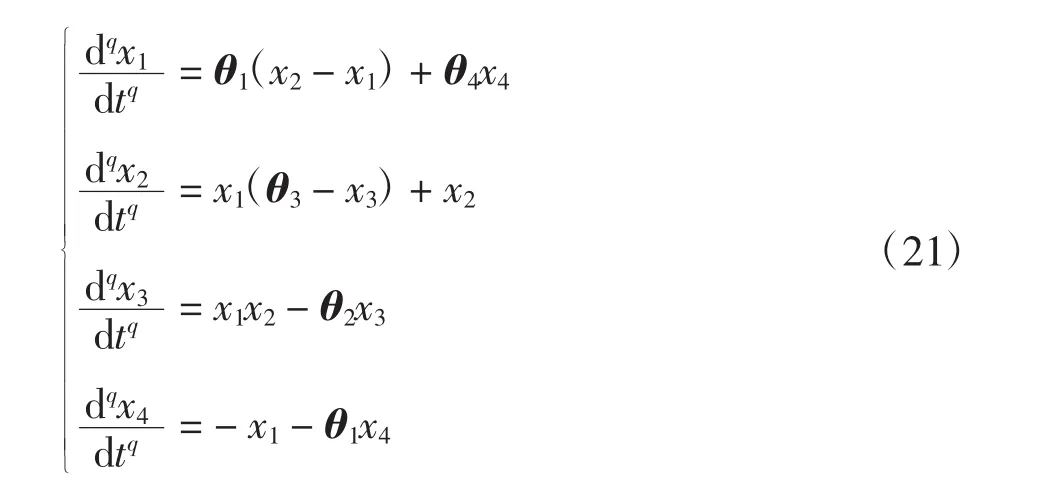
作为驱动系统，其中系统（21）的阶数q=0.98，分数阶系统的参数取（θ1，θ2，θ3，θ4）=（1，0.7，26，1.5），采用caputo定义设计算法，分数阶超混沌系统（21）的混沌吸引子图由matlab数值仿真得出，分数阶Lorenz-Stenflo超混沌系统吸引子如图1所示。

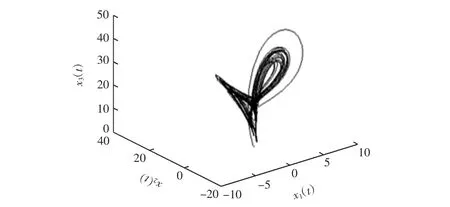
图1 分数阶Lorenz-Stenflo超混沌系统吸引子

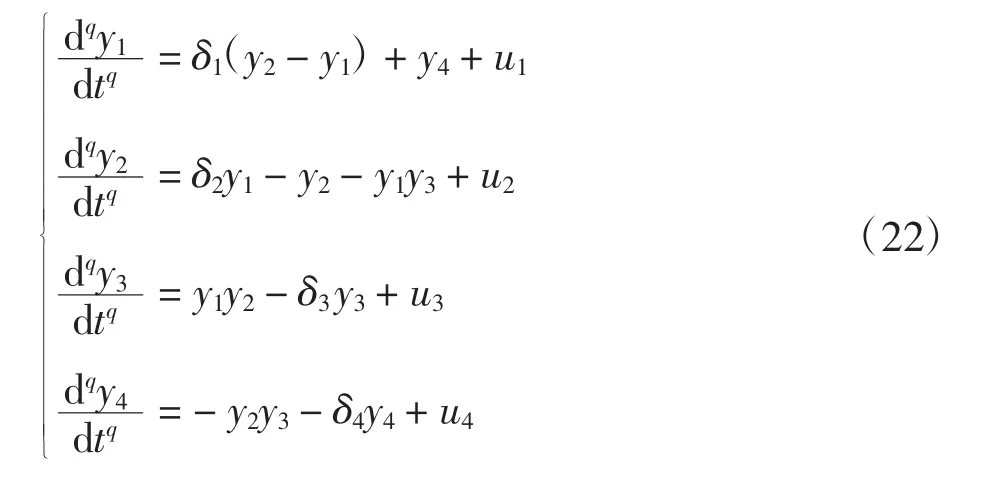
将分数阶Lorenz超混沌系统作为响应系统进行同步，其中待设计非线性同步控制器向量为 U=（u1，u2，…，un）T。在 q=0.98，（δ1，δ2，δ3，δ4）=（10，28，8/3，1）时系统出现超混沌解，分数阶Lorenz超混沌系统吸引子如图2所示。

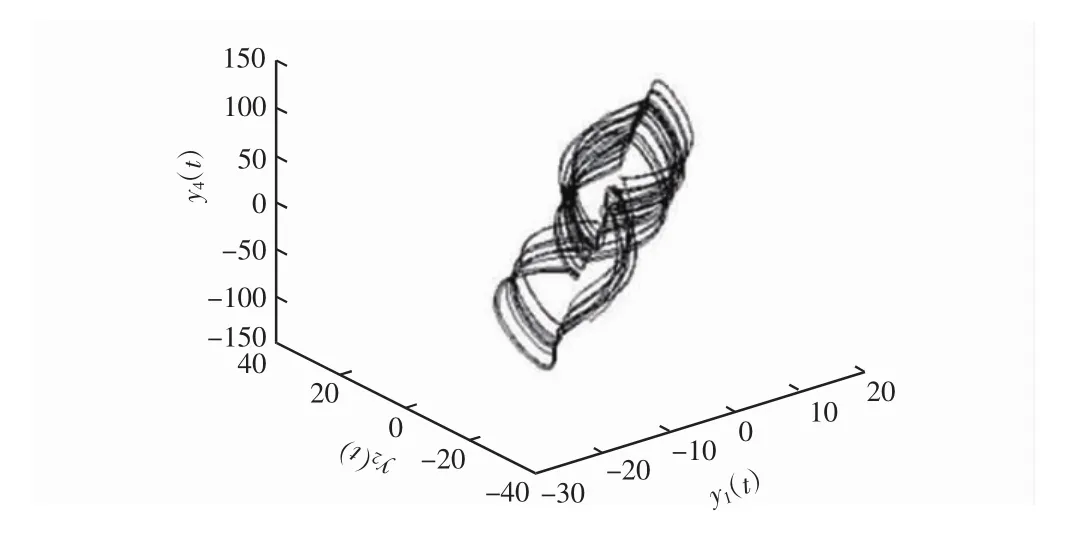
图2 分数阶Lorenz超混沌系统吸引子

假设系统 （21）、（22） 中所有参数 θ =（θ1，θ2，θ3，θ4）T，δ =（δ，δ2，δ3，δ4）T均为未知的参数向量，其估计值分别为

把系统（21）和（22）等价变换为系统（3）与（4）的形式，则

对照式（9）、（11）和（12），设计系统的控制器为：

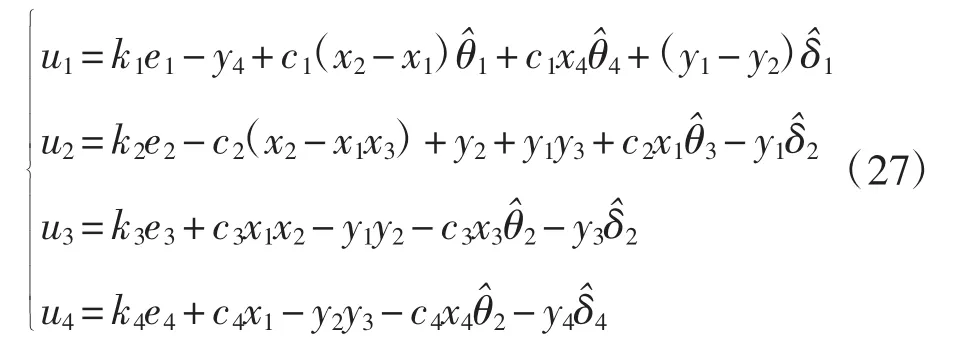
参数辨识规则为：

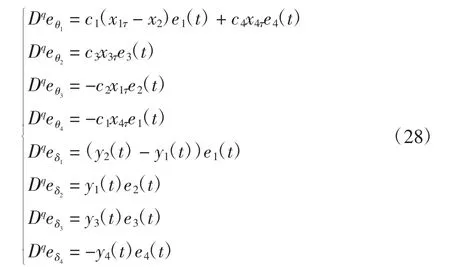
响应系统（23）中的待设计控制器选取为（28），如下的误差系统可由系统（22）和（23）相结合计算得出：

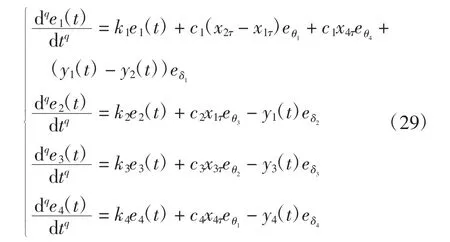
由预估矫正算法[13]，结合Matlab进行数值仿真，参数向量真实值分别为：θ =（1，0.7，26，1.5）T，δ=（10，28，8/3，1）T，选取驱动系统式（21）的初始值为：x（0）=（0.1，0.2，0.2，-0.2）T，响应系统（22）的初始值 y（0）=（-2.2，6，8.3，-9）T，误差系统（29）初始值选取为 e（0）=（3，9，7，2）T，未知参数估计值分别选取为：（4，5.7，45.5，3.5）T，反馈增益对角矩阵的值选取为：K=diag{-15，-12，-14，-12}，对角矩阵取值 C=diag{2，2，2，2}。同步误差系统演化曲线如图3所示。由图3可知，控制器实现了系统（21）和（22）的射影延迟同步。未知参数估计向量的参数辨识曲线如图4和图5所示。图4和图5表明，参数估计向量随着时间趋于无穷逐步收敛到参数向量的真实值 θ =（1，0.7，26，1.5）T与 δ =（10，28，8/3，1）T，进而说明了所给参数更新规则的有效性。

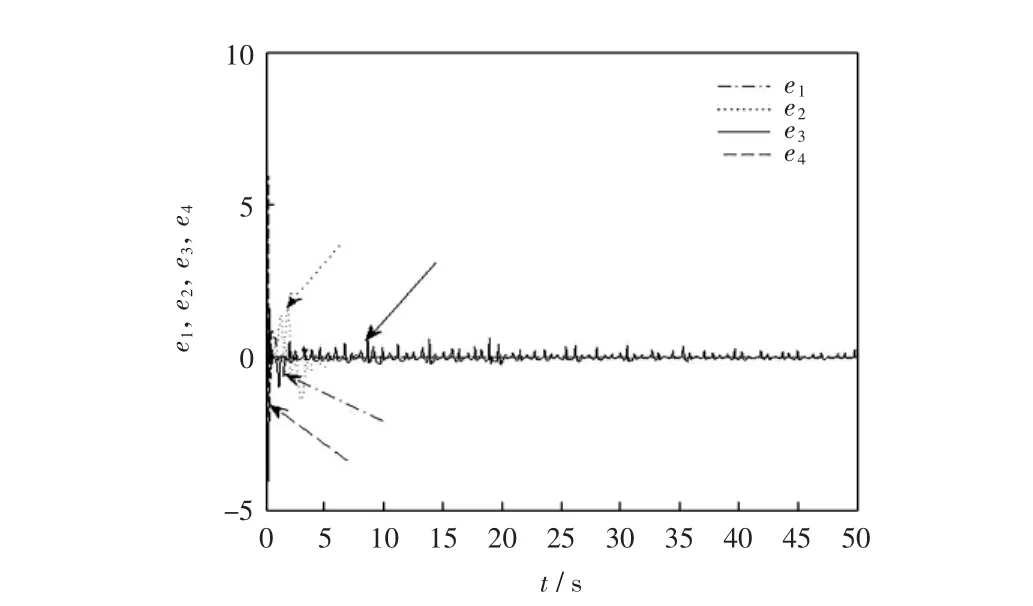
图3 误差系统演化曲线

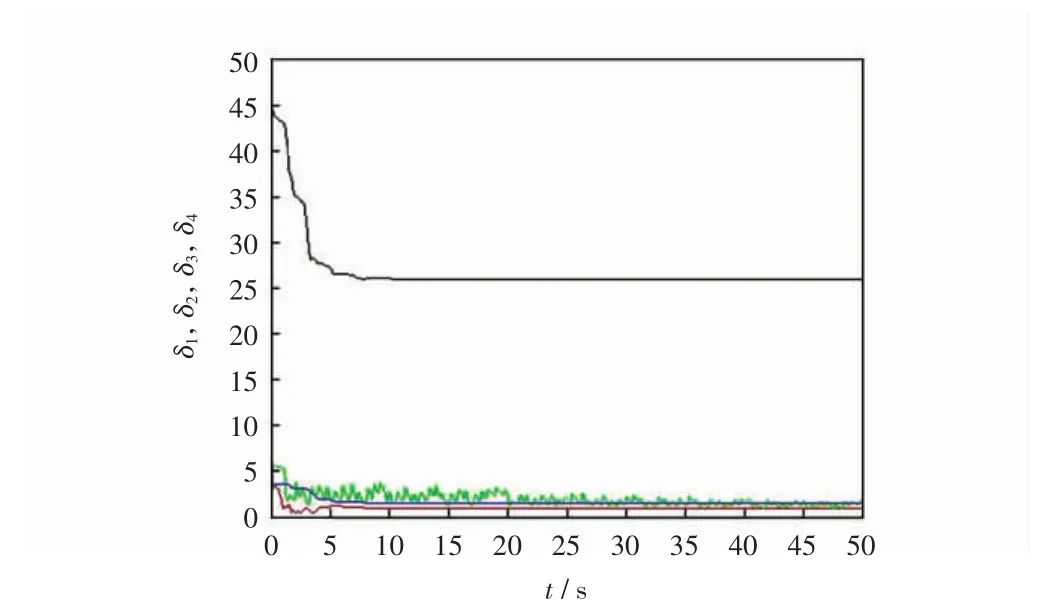
图4 驱动系统参数辨识曲线

图5 响应系统参数辨识曲线

4 结语

本文基于分数阶线性自治系统的稳定性理论，结合非线性控制方法，提出一种射影延迟同步判据，并在参数未知的情况下设计了相应的参数辨识规则。以实现分数阶超Lorenz-Stenflo混沌系统和分数阶超Lorenz混沌系统之间的射影延迟同步为例，运用Matlab数学工具进行数值仿真，分别从理论和数值上对提出的射影延迟同步方案进行了验证，验证结果证明了该同步方案中设计的控制器和未知参数辨识规则的正确性和有效性。