缩微智能车路径跟踪的增量式PID控制

何俊龙，杜 峰，关志伟，张 羽

（天津职业技术师范大学汽车与交通学院，天津 300222）

智能车的路径跟踪是指在无人驾驶情况下对智能车转向系统的自动控制，使智能车沿期望路径行驶。根据车载传感器种类，路径跟踪系统分为预瞄式系统和非预瞄式系统[1]。路径跟踪的控制方法大致可分为2种：第1种是在车辆运动学基础上，将期望路径转化为车辆动力学物理量，并将其作为被控对象，一般采用神经网络、模糊控制等方法对其误差进行消除；第2种是根据车辆与期望路径间的横向或航向偏差作为控制算法输入量，常用算法有PID、Pure Pursuit及环形预瞄法等[2]。出于对实车路径跟踪成本的考虑，智能交通行业内的大部分高校及科研院所均选择在缩微环境下进行路径跟踪实验。荷兰应用科学研究中心为测试智能车路径跟踪、避障和通信等功能，搭建了半实物仿真的智能车辆和交通模拟实验系统VEHIL（vehicle hardware in the loop）[3]。美国拉斯阿莫斯国家实验室、德国柏林交通系统研究院和麻省理工MITSIM实验室等都搭建了类似的模拟仿真系统[4]。在国内，清华大学、武汉理工大学、中国人民解放军陆军军事交通学院、重庆科学技术研究院等机构也都搭建了缩微环境下的模拟实验平台，为智能车的协同驾驶、队列行驶以及路径跟踪等功能提供了有利的实验平台[5]。本文将根据实车路径跟踪实验中的成本及时间等因素，搭建一个包含车、道路的缩微道路环境实验平台。根据缩微车与规划路径间的几何位置关系，确定缩微车的航向，并采用增量式PID跟踪算法实现对规划路径的跟踪。

1 缩微智能车路径跟踪模型的建立

缩微智能车路径跟踪的数学模型如图1所示。

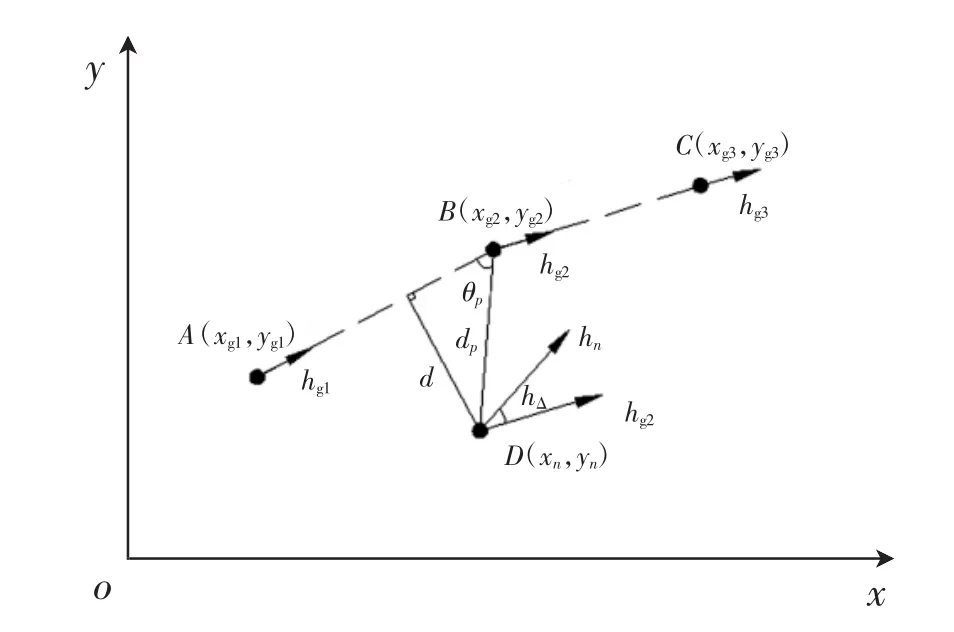
图1 缩微智能车路径跟踪数学模型

在大地坐标系xoy中，假设预设路径有3个相邻的点，坐标分别为 A（xg1，yg1）、B（xg2，yg2）、C（xg3，yg3），预设点上的航向分别为hg1、hg2、hg3。实验过程中，通过无线射频识别技术（radio frequency identification，RFID）获取缩微车在大地直角坐标系中的当前位置D（xn，yn），航向为 hn[6]。

假设当前缩微车行驶在A和B两点之间，由于A、B坐标已知，故可求得A、B两点之间的直线方程[7]为：

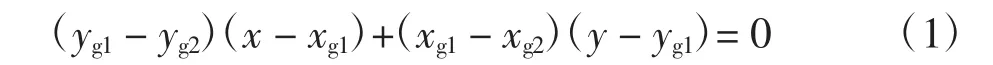
由缩微车当前位置坐标可求出车到AB直线的垂直距离为：

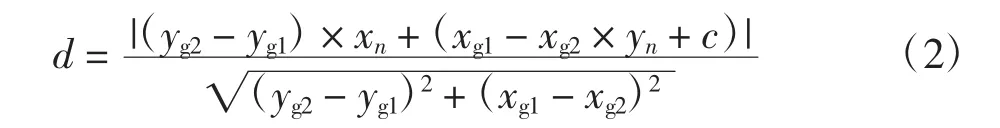
缩微车与目标点B之间的直线距离为：

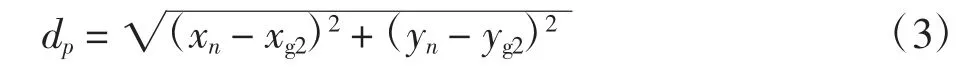
缩微车与目标点B的连线与给定路径直线AB夹角θp的余弦为：

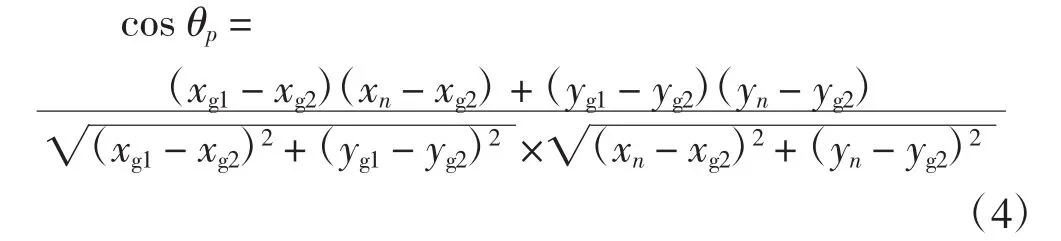
缩微车的实际航向与目标航向差为：

2 缩微智能车控制方案及控制器的设计

2.1 缩微智能车整体控制方案

缩微智能车的控制方案主要集中于对缩微车速度和角度的控制，其核心思想是：缩微智能车通过车载摄像头标定，建立图像和路面间的坐标关系，对摄像头采集到的图像中的车道线进行图像处理，从而判断道路类型。车载光电传感器获取障碍物相对于车体的位置参数，判断前方是否存在障碍物，若没有障碍，缩微车继续正常运行；若检测到障碍，则根据写入车中的控制命令决定其超车或停止。缩微智能车的相关动作都依赖于车载传感器将获取到的信息传递给车载处理器，处理器再将相应的控制指令发送给下位机，使其输出PWM方波以一定的控制策略改变电机的转速以及舵机的转角，从而实现对缩微车速度和转角的控制[8]。缩微智能车总体控制设计方案如图2所示。

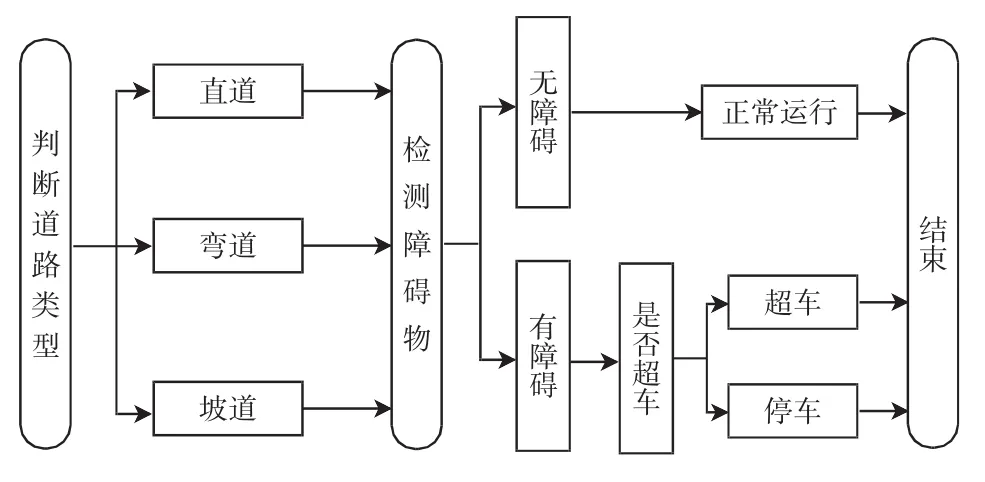
图2 缩微智能车整体控制方案

2.2 路径跟踪PID控制器的设计

2.2.1 建立路径跟踪PID控制器模型

PID控制是当前应用最为广泛的控制系统。它不仅结构简单，算法容易实现，还具有较好的鲁棒性[9]。考虑到缩微智能车的控制精度，本文选取由常规PID控制算法改进而成的增量式PID控制作为缩微智能车的控制策略。增量式PID的实现公式为：

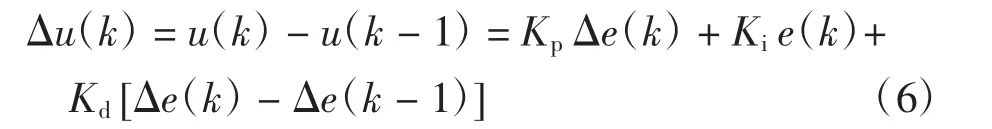
离散化增量式PID控制律为：

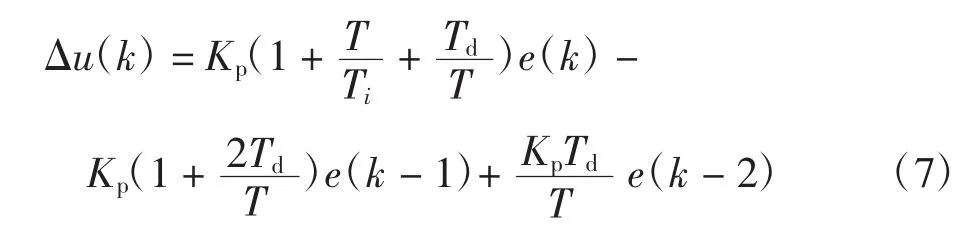
式中：e（k）为第k次采样时的设定值与实际值的差；e（k-1）为上一次采样时的设定值与实际值的差值；e（k-2）同理；Kp为比例系数；Ti和 Td分别为积分时间和微分时间；T为采样周期[10]。

PID算法中的积分环节可以减小系统静态误差，提高系统的控制精度。本文采用积分分离法对积分项进行改进。积分分离法的基本思路是：在启动、结束或大幅度增减设定时，短时间内系统输出有很大的偏差，易造成PID运算的积分积累，导致控制量超过执行机构允许的最大动作范围对应的临界值ε，从而引起较大的超调，甚至是震荡，此时取消积分作用，采用PD控制能够快速降低超调量，使系统稳定性提高；当被控量接近给定值时，引入积分控制，消除静差，提高精度。具体措施为设定1个误差临界值ε，当|ek|＞ε时，采用PD控制，即令积分项系数Ki=0；而当|ek|≤ε时，采用PID控制。根据Ki=1/Ti可确定Ki的值。

引入微分环节主要为改善闭环控制系统的鲁棒性和动态响应速度。因为微分系数主要影响控制系统误差变化速率，微分系数过大会使系统阻尼增大，导致系统调节时间过长，而过小的微分系数会使系统响应变慢，动态特性变差[11]。

2.2.2 整定PID控制器参数

PID控制器参数整定的方法很多，例如Ziegler-Nichols整定法、临界比例带法、试凑法等。但是，Ziegler-Nichols整定法的适用对象为带延迟的一阶惯性环节，临界比例带法适用对象为已知对象数学模型的场合，且被控对象为3阶或3阶以上。因此，本文采用试凑法进行PID控制器参数的整定，步骤如下：

（1）确定比例系数Kp

确定比例系数Kp时，首先去掉PID控制器的积分项和微分项，令Ti=0、Td=0，使之成为纯比例调节。比例系数Kp由0开始逐渐增大，直至系统出现振荡；再反过来，从此时的比例系数Kp逐渐减小，直至系统振荡消失。记录此时的比例系数Kp，设定PID控制器的比例系数Kp为当前值的60%～70%。调试中发现，当Kp=16时，系统振荡消失，故令控制器的比例系数Kp=10。

（2）确定积分时间常数Ti

比例系数Kp确定后，设定一个较大的积分时间常数Ti，然后逐渐减小Ti，直至系统出现振荡，然后再反过来，逐渐增大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150%～180%。调试中发现，当Ti=7时，系统振荡消失，故令控制器的比例系数Ti=10。

（3）确定微分时间常数Td

微分时间常数Td与确定Kp的方法相同，记录下系统振荡消失时的比例系数Td，设定PID的比例系数Td为当前值的30%。调试中发现，当Td=52时，系统振荡消失，故令控制器的比例系数Td=15。

增量式PID控制算法在传统算法的基础上做了一些改进，由于增量式算法不需要对误差值做累加，增量Δu（k）只与最近的k、k-1、k-2次的采样值有关，因此计算精度对控制量影响较小。增量式PID控制算法流程如图3所示。

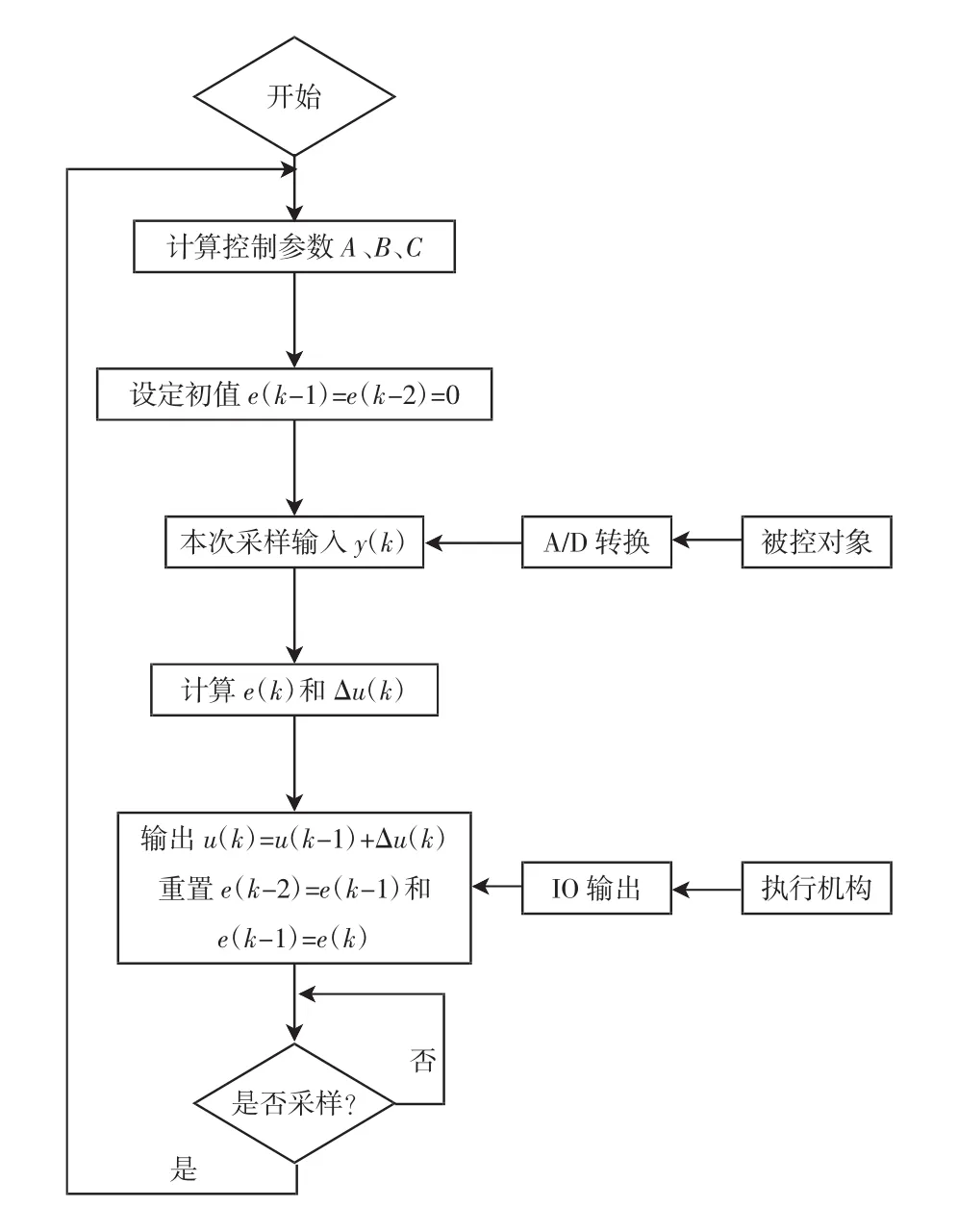
图3 增量式PID控制算法流程

3 仿真分析与实验验证

3.1 搭建缩微道路环境实验平台

缩微道路环境实验平台包含车、路2大部分。其中缩微车与原车的尺寸比例为1∶10，缩微智能车的设计速度为0～3 m/s，智能缩微车如图4所示。

该车主要包含感知模块（摄像头、光电传感器、刷卡器）、通信模块（WiFi模块）、电源模块（12 V锂电池及7.2 V镍氢动力电池）和决策与控制模块（工业主板、单片机、控制电路）。

图4 缩微智能车

缩微道路环境实验平台长3 m、宽2 m，实验平台面积越小，对车载控制器的响应时间及其稳定性的要求就越高。国内几所著名高校所建立的缩微道路实验环境大都在几十平米，甚至上百平米，尚未有在如此小的实验平台上进行智能车的相关科学研究。缩微道路环境实验台如图5所示。该实验台包括道路交通标志标线、信号灯、U形弯、坡道、收费杆等多种道路特征。缩微车装有高、低2个摄像头，高位摄像头主要负责检测车道线，低位摄像头主要负责检测交通灯和路障，然后将采集到的路况信息发送给车载处理器进行决策，再由控制系统将相应的控制指令发送给执行器，使智能车完成相应的动作。

图5 缩微道路交通实验台

3.2 仿真分析

仿真实验分为2组，分别将智能小车的速度设定为1.5 m/s和3 m/s。系统的输入为单位阶跃信号，对舵机进行位置控制。设系统采样时间T=0.01 s，设计PID 控制器为：Kp=10，Ti=10，Td=15，ε =5°。当|ek|＞5°时，采用PD控制，即令积分项系数Ki=0；当|ek|≤5°时，采用PID控制。增量式PID控制器输出设定上限幅5°，下限幅-5°，即缩微智能车转角每次的最大变化量为5°。2组实验都将缩微智能车的初始航向设定为10°，计算机记录缩微智能车的航向变化，并绘制出PID控制器响应曲线。车速为1.5 m/s和3 m/s时的PID控制器响应曲线仿真结果如图6和7所示。

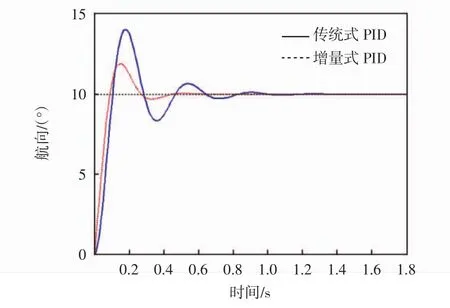
图6 1.5 m/s时PID控制器响应曲线

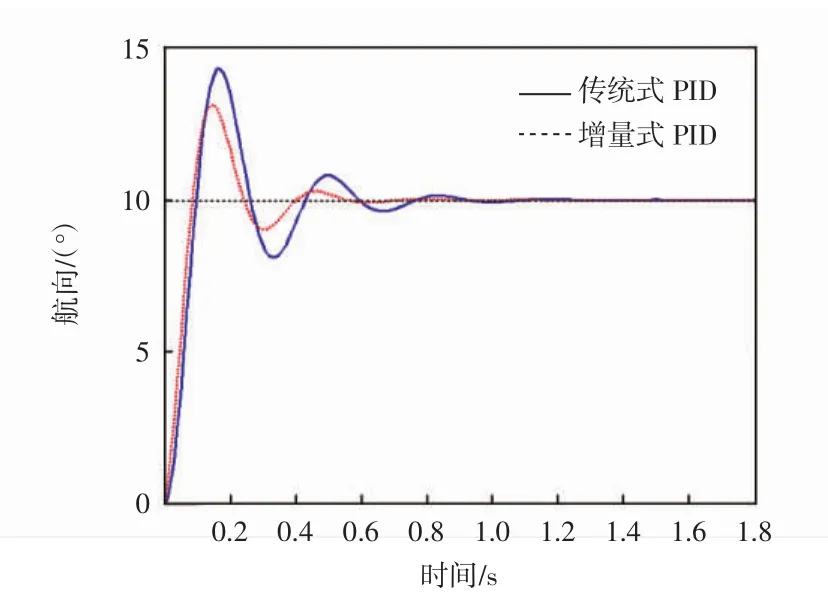
图7 3 m/s时PID控制器响应曲线

从图6和图7可以看出，改进后的增量式PID控制算法无论低速还是高速情况都缩短了系统的上升时间和调整时间，使系统的响应速度加快，同时系统的超调量也有所降低，即当缩微车的行驶航向与预设路径航向有偏差时，该算法能够迅速对输出值做出调整，使缩微车按预设航向前进。

3.3 实验验证

缩微车上安装的读卡器可以与道路上的射频卡进行信息交互，将缩微车的位置信息反馈给上位机。根据所得到的位置及航向角，利用增量式PID控制算法调节舵机转角，使缩微车按期望路径行驶。车速为1.5 m/s和3 m/s时传统式PID和增量式PID控制器的路径跟踪曲线分别如图8所示和图9所示。

实验结果表明：传统PID控制下，缩微车跟踪直线道路的最大偏差为0.12 m，跟踪弯道的最大偏差约为0.2 m；增量式PID控制下，缩微车跟踪直线道路的最大偏差为0.05 m，跟踪弯道的最大偏差约为0.15 m。本文所设计的增量式PID控制器，较好地实现了不同车速下对期望路径的跟踪，缩微车转向系统能够快速、准确地对舵机的转角进行控制。改进后的算法增强了系统的稳定性，即在路径跟踪过程中，缩微车能够更加稳定地沿着预设路径行驶。

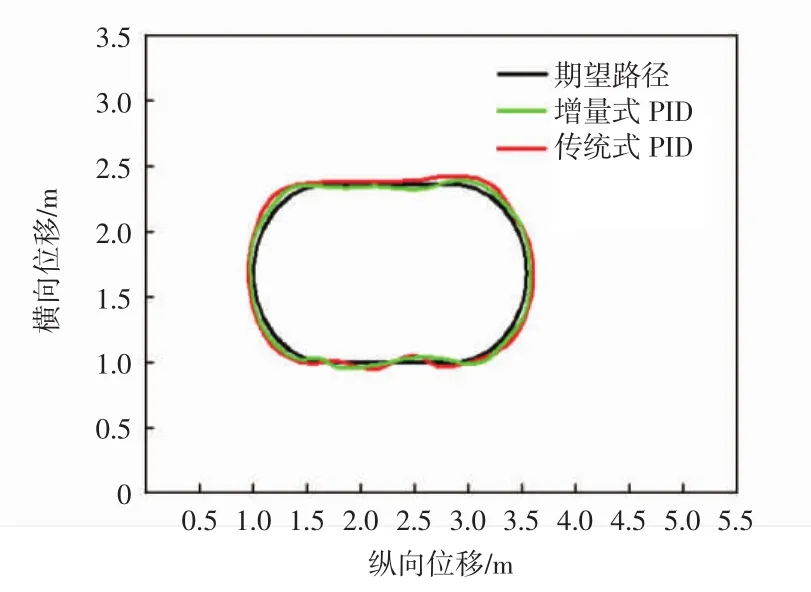
图8 1.5 m/s时路径跟踪曲线

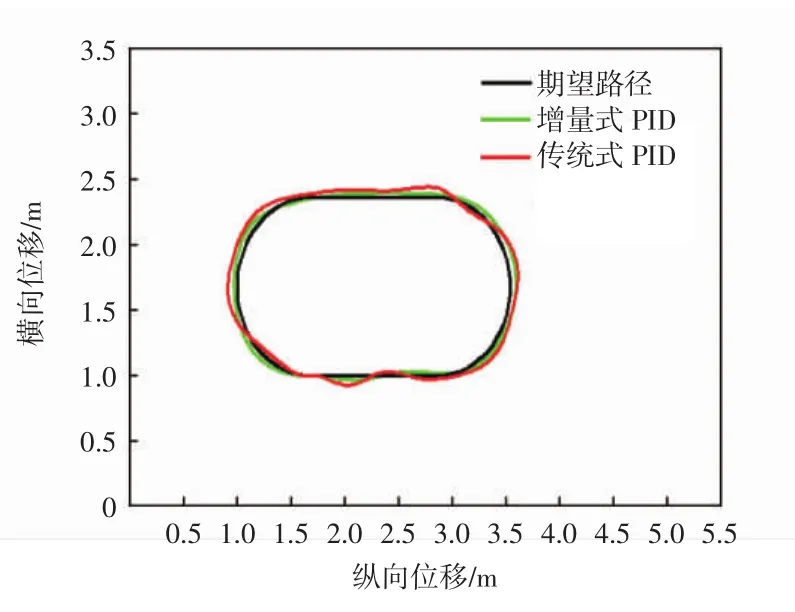
图9 3 m/s时路径跟踪曲线

4 结 语

本文基于预设目标点的位置和缩微智能车当前位置，设计了缩微智能车的路径跟踪模型。该模型可根据缩微车当前位置及航向与预设路径之间的几何位置关系，得出缩微车实际航向与目标航向的差值。基于增量式PID算法，在Matlab上完成了路径跟踪仿真，仿真结果表明，该算法在不同车速条件下均能够确保缩微车转向系统快速、准确地对舵机进行控制。根据缩微车反馈到上位机的车辆位置及航向角等参数，在搭建的缩微道路实验环境中实现了缩微车的路径跟踪，跟踪过程中路径偏差较小且缩微车摆动幅度适中，确保了缩微车在行驶过程中的稳定性。