一次华南暴雨的可预报性分析

刘 蕾，李宜爽，陈茂钦，张凌云

（1.广西柳州市气象局，广西 柳州 545001；2.中国人民解放军95337部队，广西 柳州 545001）

引言

大气是一个混沌非线性系统，有时一个很小的初始误差可以演变成很大的误差，从而对结果造成巨大的影响，大气可预报性的概念也由此提出［1，2］。关于大气的可预报性研究，卞建春和杨培才［3］从非线性角度重新解读了Von Neumann提出的大气运动三个分类，指出大气过程预报问题中存在两类不确定性：初始条件的不确定性和外强迫条件的不确定性。丁瑞强和李建平［4］利用非线性局部Lyapunov指数研究可预报性问题，真正地实现了对可预报性的定量化研究。对于中小尺度的可预报性，李建平和丑纪范［5］提出中小尺度系统运动的适应问题虽然是非线性的，但是仍然有快的适应过程和慢的演变过程，这说明中小尺度运动仍然具有可预报性。近年来，许多学者［6-14］利用数值模式研究了暴雨及可预报性的影响，对于初始场误差对可预报性的影响研究，丁瑞强和李建平［15］研究指出当系统的初始误差和参数误差单独存在时，系统的可预报期限随误差大小的变化规律相同，对于相同的误差大小，初始误差和参数误差对系统可预报期限的影响几乎相同，这一结果基本不随参数范围的变化而变化。对于静力平衡模式和非静力平衡模式对可预报性的影响，谭晓伟和陈德辉［16］通过比较表明，非静力平衡模式中，初始场对可预报性的影响比静力平衡模式更大。陈明行和纪立人［17］研究了误差的增长演变过程，结果认为小尺度误差自身增长较快，并通过各尺度之间的相互作用，小尺度误差向大尺度和行星尺度误差转移，从而导致整个系统的误差增长较快。

华南地处低纬，地形复杂，对华南暴雨的水汽、热量及不稳定能量输送具有重要作用的南海上观测资料有限性，导致模式对华南暴雨，特别是暖区暴雨的可预报性稍差于江淮一带的锋面暴雨［18］。目前数值预报已成为日常天气预报业务中的主要工具，而初始场的精确程度又直接影响暴雨的预报准确率和预报时效，因此利用数值模式研究初始场对暴雨可预报性的影响具有现实意义。2009年6月30日20时～7月5日20时，受高空槽、切变线及西南急流共同影响，华南出现了一次连续强降水天气过程，其中广西柳州在7月2-3日出现了严重的洪涝灾害，据有关部门统计，柳州市及各县受灾人口达75.2万人，直接经济损失9.34亿元。本文拟通过此次典型的华南暴雨个例模拟试验，考察初始场误差对华南暴雨可预报性的影响，以期更深入地理解模式的模拟能力，为业务上更好地释用模式提供一定的理论参考。

1 模式简介及模拟结果检验

为了考察模式初始场误差对华南暴雨可预报性的影响，本文利用非静力中尺度模式WRFV3.2.1版本，采用NCEP／NCAR每6小时一次的全球客观分析资料（水平分辨率1°×1°）作为模式的初始条件和侧边界条件对2009年7月2日20时～7月3日20时广西柳州的特大暴雨进行数值模拟试验，积分时间为7月2日08时～7月 3日20时共积分 36小时，模式结果为每小时输出一次。控制试验采用了双重嵌套网格，第一层网格数为107×184，分辨率为45Km，第二层分辨率为15km，网格数为98×169。表1为模式中主要的参数化方案。

表1 模式参数化方案设计

下图给出了广西范围内2009年7月2日20时～3日20时24h降雨量实况（图1a）和控制试验降雨量（图1b）。分析实况雨量可以看到，广西范围内有两条雨带，主雨带呈带状分布位于广西北部，降水中心位于柳州西北部山区（109°E，25°N），中心雨量为270mm。对比实况雨量，WRF模式较好地模拟出了此次降水的主要雨区，从图1b可以看出，控制试验模拟的降水中心位于（109°E，24.8°N），强降水落区与实况基本一致，模拟24小时雨量约为270mm，接近实况。从模式模拟的雨带分布和降水中心强度来看，模式模拟出了此次强降水主要雨带的分布及暴雨中心强度和位置。因此，可以认为此次试验较为成功，可以用其模式输出的结果进行初始场的敏感性试验。

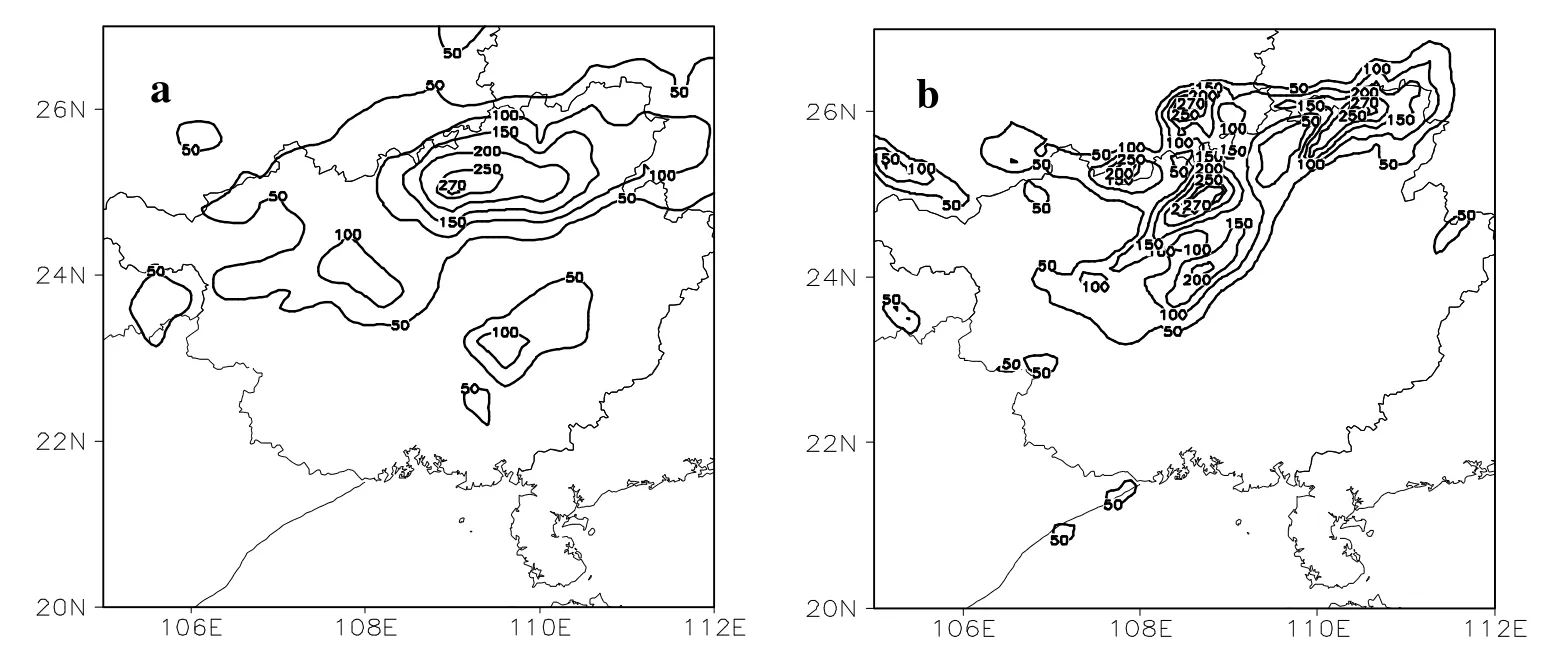
图1 2009年7月2日20时-3日20时24小时降水量（单位：mm）（a）实况；（b）控制试验

2 初始误差对华南暴雨可预报性的影响分析

2.1 方案设计

为了较好地考察误差在本次暴雨过程中的增长演变过程，在控制试验模拟效果较好的情况下，对此次暴雨控制试验的初始场添加满足均值为0，振幅为1的标准正态分布随机的初始误差，构造敏感性试验成员。分别在此次暴雨的湿度场（QVAPOR）、温度（T）和风场（U，V）的初始场上添加误差，误差振幅分别取为 0.1%，1K，2m·s-1，2m·s-1［19］。 按照这个方案，对此次暴雨控制试验初始场的QVAPOR，T，U，V分别增加和减去高斯误差，得到8个敏感性试验成员，分别命名为 aq，at，au，av，mq，mt，mu，mv。在敏感性试验中，只在初始场的第一重区域上添加误差，边界场上不添加误差。通过分析误差在模拟过程中的增长演变情况，讨论此次暴雨的可预报性问题。

2.2 集合成员总能量偏差分析

为了从定量上描述敏感性成员与控制试验之间的差别，计算了暴雨主要区域的总能量偏差，所指主要区域为以模拟中心经纬度为中心的一个81个格点×61个格点大小的区域。下文计算集合离散度也是指主要区域的集合离散度。总能量偏差的计算方法参照文献［19］，其计算方法为：

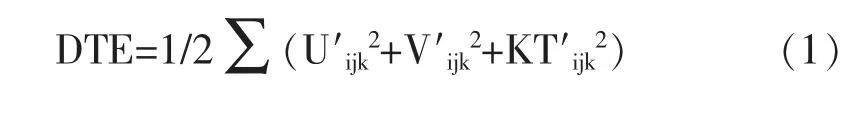
其中U′是控制试验与敏感性试验的纬向风的差值，V′是经向风的差值，T′是温度的差值。 i，j，k 分别为模式x方向，y方向，垂直方向的格点数。K＝Cp／Tr，Cp 为定压比热，一般取 1004.6m2s-2k-1，Tr为参考温度，一般取 287K［19］。

分析此次暴雨8个敏感性成员的总能量偏差随时间的演变图（图2，见彩页），可以看到，随着积分时间延长，各个敏感性试验成员的DTE都缓慢的增长。从整个积分过程来看，添加在温度场和风场上的误差增长相对较小，且增长比较平缓，积分17小时以后增长才开始加速；而添加在湿度场上的误差增长比较迅速，且数值远大于添加在温度场和风场上的误差。说明在此次暴雨模拟过程中，添加在初始场的误差随着积分过程延长，对模拟结果的改变逐渐增大，且湿过程的扰动更为敏感，造成的误差改变也更大。在日常的观测中，误差的发生是不可避免的，这些误差在模式的积分过程中不断增长，最终使得模式结果与实际降雨结果相差甚远，从这个意义上来说，模式对暴雨的可预报性随着积分时间的增长而不断变差。

2.3 集合成员离散度对比分析

离散度是表征集合成员之间不一致的量，一般来说，离散度大，可预报性就差。本文参照集合预报的方法，把加了扰动误差的敏感性成员认为是集合预报的成员，参照文献［19］计算其集合离散度，计算公式为：

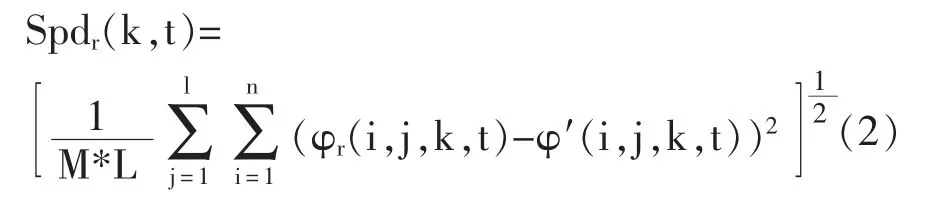
其中i，j，k分别为模式x方向，y方向，垂直方向的格点数，t为模拟时间，φ′（i，j，k，t）为敏感性成员的平均值。L为纬向方向上的格点数，M为经向方向上的格点数［19］。

图3（见彩页）分别是此次暴雨8个敏感性成员关于温度（a）、纬向风（c）和经向风（e）的区域离散度随时间的演变图以及积分到20小时关于温度（b）、纬向风（d）和经向风（f）的离散度随模式层次的变化图。由图3a可以看到积分开始以后，各集合成员的离散度都开始增长，其中湿度扰动成员的离散度增长最快。从增长的规律来看，积分的前7个小时，离散度增长迅速，然后有一个回落过程，到积分10小时后离散度又开始增长。分析积分到第20小时此次暴雨关于温度的离散度随模式层次的变化图（3b），可以发现随着模式层次的升高，各敏感性成员的离散度有所减小，但在21层以上，暴雨敏感性成员的离散度有一个快速增长的过程。分析纬向风（3c）、经向风（3e）的区域离散度随时间的演变图，发现随着积分时间的增长，敏感性成员的离散度的持续增长。从其积分到第20小时纬向风（3d）、经向风（3f）的离散度随模式层次的变化图可以看到，随着模式层次的升高，离散度缓慢的增长，从13层开始迅速的增长，到第21层时各成员的离散度都达到最大，此后离散度开始下降，且湿度场敏感性成员的离散度最大。

分析三个要素的离散度增长情况，初始场的误差对各物理量的影响不尽相同，尤其是在空间上的影响。对于温度来说，初始场上的误差造成的影响主要集中在21层以上，对低层温度的影响不大。而对于风场来说，初始场上的误差造成的影响主要集中在21层以下。对高层风场的影响不大。这种在空间上的不一致反映误差在物理量场的传播具有各向异性的特点。从敏感性成员来分析，无论是离散度随时间的增长，还是随模式层次的增长，都是湿度场上的误差导致的离散度最大。而从空间上来说，模式对高层温度的预报能力较差，对低层风场的预报能力较好。

2.4 初始场误差对总雨量影响的分析

图4（见彩页）为控制试验与8个敏感性试验成员模拟总雨量的差值图。从图4a，图4e来看，差值的大值区主要有三个，最大的差值区集中在暴雨的中心区域，数值达到100mm以上。说明添加在初始湿度场上的扰动随着积分过程的增长不断影响模拟结果，最终导致了模拟结果的改变。分析图4b，图4f可以看到，差值大值区形态与雨区的形态比较一致，有三个大值中心，但数值比湿度场扰动的成员要小。从图4c，图4g看出，虽然纬向风场上的误差也一样导致了模拟结果的较大改变，但是与其它敏感性成员相比，造成的误差范围和数值都较小。而经向风场的误差造成的模拟结果改变较大（图4d，图4h），这一结果反映此次暴雨降雨量场模拟结果对纬向风场上的改变不太敏感，而对经向风场的改变十分敏感。总体来看，敏感性试验成员与控制试验的雨量差值都比较大，在整个降雨区域都产生了差值，大值中心主要产生在暴雨中心。罗雨和张立凤［20］的研究也指出初始热力要素的误差是造成降水预报误差的主要原因，湿物理过程是误差发展的主要机制，相应的凝结加热是误差增长的重要能量来源。在暴雨的中心区域，由于对流旺盛，湿物理过程发展迅速，因此也导致了误差增长迅速。

添加在初始场的微小误差，经过积分过程后，对模拟结果的改变不尽一致，此次暴雨的模拟结果对水汽场的扰动十分敏感，对温度场的扰动次之，而对经向风的扰动则较纬向风的扰动更加敏感。这一结果表明本次华南暴雨的可预报性与水汽场的精确度有关，水汽初始场越准确，暴雨的模式可预报性就越长；初始风场对暴雨模拟结果主要体现在经向风场的影响上，经向风场越准确，暴雨的可预报性就越好。

3 主要结论

本文以2009年7月2－3日华南暴雨为例，利用WRFV3.2.1数值模式通过对控制试验的初始场添加符合高斯分布的初始误差，考察初始场对暴雨数值模拟的影响，以此讨论本次华南暴雨的可预报性问题，得出以下结论：

（1）随着积分时间的增加，添加在初始场的误差对模拟结果的改变逐渐增大，且湿过程误差造成的误差改变更大。

（2）分析集合成员离散度发现其与总能量误差的增长规律类似，随着积分时间的延长，各敏感性成员的离散度都逐渐增大，初始场上的误差导致成员间的分歧增大，其可预报性降低。而从空间上来说，模式对高层温度的预报能力较差，对低层风场的预报能力较好。

（3）通过分析初始误差对总雨量的影响，表明暴雨的可预报性与水汽场的精确度有关，水汽初始场越准确，暴雨的模式可预报性就越长；初始风场对暴雨模拟结果主要体现在经向风场的影响上，经向风场越准确，暴雨的可预报性就越好。

在日常观测中，误差的发生是不可避免的，即使是经过资料同化处理过的初始场与理想的初始场相比仍然存在误差，这些误差在模式的积分过程中不断增长，最终使得模式结果与实际降雨结果相差甚远。日常预报业务中，对模式预报性能的熟悉有利于我们更好地解释释用模式的模拟结果，因此对模拟结果的检验及对比分析是了解模式性能的可靠途径。

［1］Thompson，P.D.Uncertainty of initial state as a factor in the predictability of large scale atmospheric flow patterns ［J］.Tellus，1957，9：275－295.

［2］Lorenz，E.N.The predictability of hydrodynamic flow Trans ［J］.New York Acad.Sci.，1963，25B：409－432.

［3］卞建春，杨培才.关于大气过程可预报性问题的一些讨论［J］.高原气象，2003，22（4）：315－323.

［4］丁瑞强，李建平.初始误差和参数误差对混沌系统可预报性影响的比较 ［J］.地球物理学报，2008，51 （4）：1007－1012.

［5］李建平，丑纪范.非线性大气动力学的进展［J］.大气科学，2003，27（4）：653－672.

［6］陈炯，郑永光.WRF模式中不同边界层参数化方案对2003年7月江淮暴雨的数值模拟及其比较［C］.中国气象学会 2003年年会论文集 （7），北京，气象出版社，2003：221－224.

［7］王建捷，周斌，郭肖容.不同对流参数化方案试验中凝结加热的特征及对暴雨中尺度模拟结果的影响［J］.气象学报，2005，63（4）：405－417.

［8］陈静，薛纪善，颜宏.物理过程参数化方案对中尺度暴雨数值模拟影响的研究［J］.气象学报，2003，61 （2）：203－218.

［9］李刚，王铁，谈言科，等.WRF3.0参数化敏感性及集合预报试验 ［J］.解放军理工大学学报 （自然科学版），2010，11（1）：89－96.

［10］黄海波，陈春艳，朱雯娜.WRF模式不同云微物理参数化方案及水平分辨率对降水预报效果的影响［J］.气象科技，2011，39 （5）：529－536.

［11］廖镜彪，王雪梅，夏北成，等.WRF模式中微物理和积云参数化方案的对比试验［J］.热带气象学报，2012，28（4）：461－470.

［12］邓明，杨亚钦，李江南.城市下垫面对华南地区前汛期暴雨的影响初探 ［J］.气象研究与应用，2017，38（3）：23－25，30.

［13］叶朗明，陈明慧，夏冠聪.华南一次特大暴雨诊断分析及数值模拟［J］.气象研究与应用，2014，35（3）：20－26.

［14］何文勇，麦雪湖，欧坚莲，等.多普勒雷达资料同化对暴雨过程模拟的影响 ［J］.气象研究与应用，2013，34（3）：61－64.

［15］丁瑞强，李建平.误差非线性的增长理论及可预报性研究［J］.大气科学，2007，31（4）：571－576

［16］谭晓伟，陈德辉.观测系统影响试验与可预报性研究［D］.北京：中国气象科学研究院，2005.

［17］陈明行，纪立人.数值天气预报中的误差增长及大气的可预报性［J］.气象学报，1989，47（2）：147－155.

［18］陈茂钦，徐海明，刘蕾，等.WRF3.1微物理参数化方案对两例暴雨的集合预报试验及可预报性分析［J］.气象科学，2012，32（3）：237－245.

［19］陈茂钦，徐海明.江淮锋面和华南暖区两次暴雨过程的可预报性对比［J］.南京信息工程大学学报（自然科学版），2011，3（2）：118－127.

［20］罗雨，张立凤.一次梅雨锋暴雨预报中的误差演变规律和可预报性分析［J］.气象学报，2010，68（3）：411－420.