对称四极测深AB/2距的有效探测深度改算模型

秦飞，赵明亮，李庆华，陶琳



对称四极测深AB/2距的有效探测深度改算模型

秦飞1，2，赵明亮1，李庆华1，陶琳1

（1. 四川省地质矿产勘查开发局四〇三地质队，四川 峨眉 614200；2. 成都理工大学，成都 610059）

在学习总结前人对常规电法对称四极测深AB/2距有效探测深度研究成果的基础上，结合多年实际工作经验，得出同一测区，随着AB/2距不断增加其探测有效深度的变化规律曲线为一条“类似反正切函数曲线，曲线函数式为：H=K·arctg(（AB/2）/N)；当 AB/2逐渐增加，初始段是近似正比增加，随后有效探测深度增加越来越小，最后段增加值趋于0。根据以上理论建立了对称四极测深AB/2距的有效探测深度深度改算模型图，并在模型图上划分出了有效区、过渡区、无效区，该模型图对实际工作有较好的指导作用。

电法勘探；四级测深；AB/2距；深度改算模型

电阻率法的有效探测深度的影响因素较多，主要取决于以下四个方面：一是被探测地质体本身的因素，如大小、形状、埋深及与围岩的电阻率差别；二是供电电极距（AB/2）的大小；三是观测精度；四是地形和不均匀体的干扰。常规电法到底能测多深，这一问题一直困惑着众多的地球物理工作者，不少学者对这一问题进行了较多的研究，也取得了一定的进展。关于供电AB/2电极距与有效探测深度关系的问题，在理论上伸缩性很大，很难定出统一标准，但在小区域内，总会有一定的规律性，摸索认清出它们之间的规律，对于指导我们的实际工作具有较大的意义。

Schlumberger(1932)提出了不同情况下对称四极测深供电AB/2距与勘探深度的关系，认为一般情况AB/2距等于深度，有覆盖层（两层）的情况下AB/4距等于深度，复杂的水平多层情况下AB/8距等于深度。赵和云、钱家栋等人在1982年对电阻率法中勘探深度和探测范围的理论讨论和计算时指出，在均匀介质、四极对称装置最大深度可达极距AB的1.5倍。河南省地矿厅第一地质调查队李治时等人开展激电对称四极测深方法确定黄土覆盖层下砂岩中的富水深度，其深度是用AB/2乘以校正系数K（工区AB/2最大极距250米，K值是1.27），工程验证精度均较高。内蒙古自治区哲里木盟水利处的魏盎等人根据多个钻孔工程验证（202个钻孔）总结出AB／2与勘探度度关系，认为按1～0.33的分段改正系数进行改正其效果较好。黑龙江省肇州县水务局的丽红等人经过3年上千个点的测量证实，以AB／2为测量深度，当AB/2距小于200m时，工程验证误差较小。山东省水利科学研究院刘春华等人在基岩地区找水工作中，历时30余年，对AB/2距代表的深度进行了总结，用电阻率找水基岩地区AB/2分段深度修正系数是1～0.5（AB/2距在500m以内）。

1 AB/2距的有效探测深度确定的几个实例

例1：2003年，我队在四川会东淌塘铜矿，采用（双频激电）测深，在地形线下直接作图法形成的原始图上，根据异常顶部标高推出见矿深度200m，工程验证220m见厚大的隐伏矿，误差20m。

例2：2005年，我队在会东铁柳铅锌矿，采用（双频激电）对称四极测深，在地形线下直接用AB/2距为深度作图，高极化异常区推测为极化体的顶部埋深206m，后经工程验证见矿，误差1m。

例3：2008年，我们在巴塘夏塞银铅锌矿区开展激电对称四极测深，实达深度用K *AB/2，K值的确定，用已知勘探线（数个钻孔工程控制）上方法试验，用实测AB/2距作图与已知对比，不断的修改拟合而得出分段改正的K值系数，其结果如下：

①当AB/2距≤50m时，K=1；②当AB/2距 51～100m时，K=0.93；③当AB/2距 101～150m时，K=0.88；④当AB/2距 151～200m时，K=0.8；⑤当AB/2距 201～250m时，K=0.7；⑥当AB/2距 251～300m时，K=0.6。用上述方法作分段改正，在矿区外围推测的极化体，经工程验总体误差较小。

例4：四川神白玉有热矿区在39线开展双频激电测量，用AB/2距作图，激电异常顶部埋深为400m，结合地质进行钻孔工程验证，在异常体顺延深度至550米处钻孔揭露见金属硫化矿。

2 AB/2距的有效探测深度变化规律认识

从上述文献成果并结合多年工作经验，认为AB/2距在不同地质条件下实际探测深度也有较大差异。在同一条件下，AB/2距的有效探测深度的变化规律是一条“类似反正切函数曲线”（即曲线为：H=K·arctg(（AB/2）/N)，其变化规律如下：

1）AB/2距较小段，即10～100m段，AB/2距与实际深度基本相同。

2）AB/2距100～300m段，AB/2距比实际探测的有效深度要逐渐偏小； AB/2距的从100增加到300m这段，大部分情况近似等比增加。

3)AB/2距300～500m段，增加AB/2距对应增加的有效探测深度很小。

4)AB/2距大于500m后，随着AB/2距的增加有效探测深度增加的更小，且数据质量较差。

5)无论测区地电情况多好或多坏，当AB/2距增大到一定程度后（大约是300～800m后不同地质条件深度不同），难以采集到有效数据。

3 AB/2距的有效探测深度改算验模型建立与使用

依据总结认识规律性，依据Y=K·arctan（x/N）函数曲线，取不同的K、N值可得出不同形态的反函数曲线来。实际情况的是多种，概略地将野外不同测区的情况大致划分为9种，从而绘制出9条对称四极测深AB/2距有效探测深度改正曲线。其中：

曲线H1=80×arctg（（AB/2)/100)，代表探测深度特浅测区的改正曲线;

曲线H2=100×arctg(（AB/2)/120)，代表探测深度极浅测区的改正曲线;

曲线H3=130×arctg(（AB/2)/140)，代表探测深度十分浅测区的改正曲线;

曲线H4=160×arctg(（AB/2)/160)，代表探测深度比较浅测区的改正曲线;

曲线H5=190×arctg(（AB/2)/180)，代表探测深度略浅测区的改正曲线;

曲线H6=220×arctg(（AB/2)/200)，代表探测深度一般测区的改正曲线;

曲线H7=250×arctg(（AB/2)/220)，代表探测深度较深矿测区的改正曲线;

曲线H8=280×arctg(（AB/2)/240)，代表探测深度比较深测区的改正曲线;

曲线H9=310×arctg(（AB/2）/260)，代表探测深度十分深测区的改正曲线。

另外，依据生产工作经验，在模型图上划分出有效区、过渡区、无效区，其中，有效区AB/2距相对较短，无效区AB/2距相对较长，在生产使用时应注意如下几点：

1）建立的9条对称四极测深AB/2距有效探测深度改正模型曲线，曲线形态为一条类似反正切函数曲线，各曲线高低不同主要反应各个测区探测地质体本身不同以及各个测区具体电性结构条件的差异性，使其同一方法技术在同一矿区AB/2距的有效探测深度随着极距的不断培加也会发生不同的变化。

2）实际工作中，通过测区已知工程的验证情况或相邻地区的工作经验选择图1中的具体改算曲线进行改正，也可试选多条曲线进行改算成图对比其效果后择优选一。

3）将模型图中的每条改正曲线视为磁法勘探的某天的日变曲线（AB/2视为时间，改正深度视为T），用一般的磁法软件可实现快速自动改正；当然还可将模型图编程，改正时实现快速自动化。另外，还可直接用建立的反正切函数公式，在excel电子表格中计算。

4）对这一模型认识后，结合各个矿区具体情况，在工作设计时便于选择比较符合实际的最大AB/2极距，特别注意，不能为了得到人为想象的有效探测深度无条件地将AB/2距设为很大，必将是一个费力不起作用的结果。

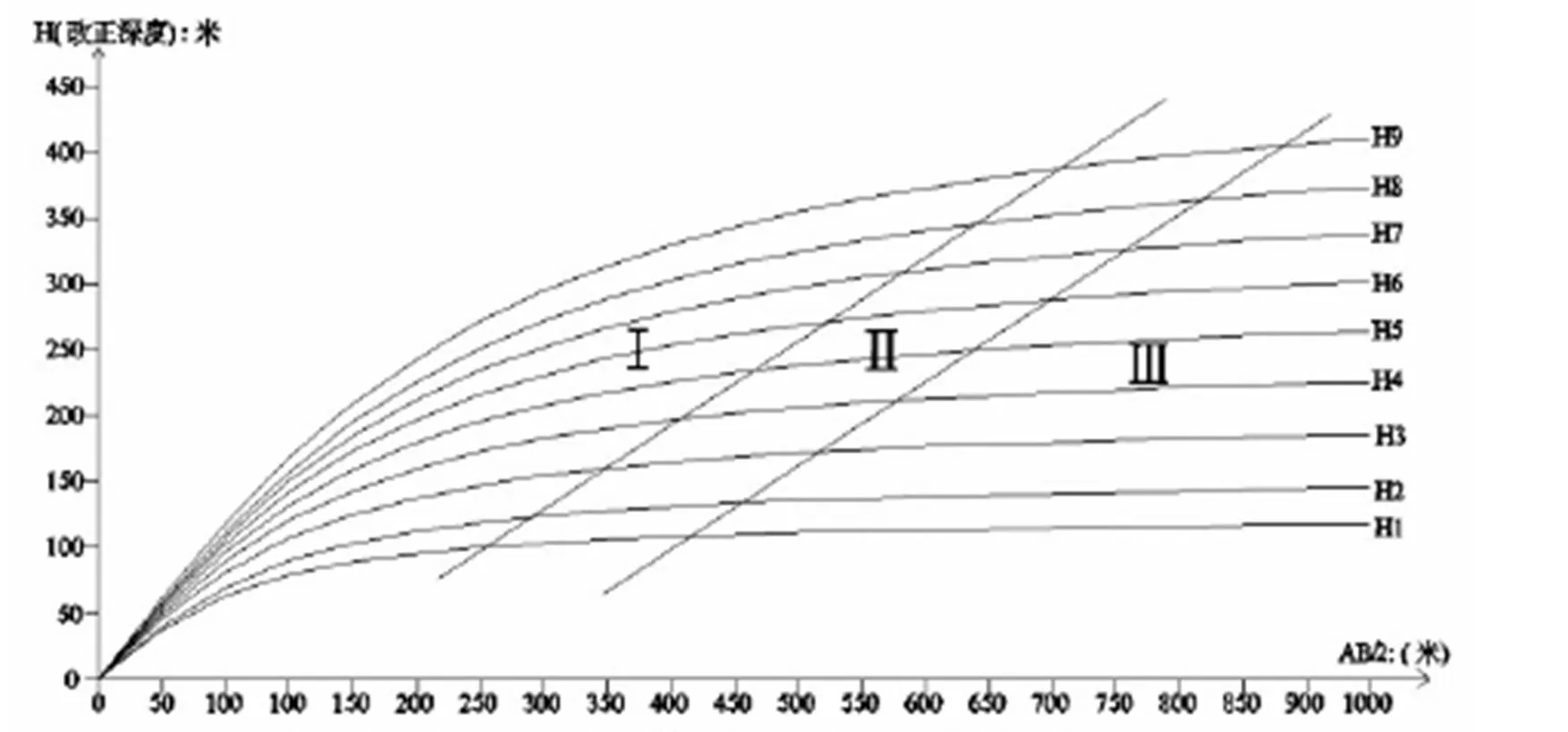
激电对称四极测深AB/2距有效深度计算模型图

H1~H9：由浅到深不同深度的测量曲线 Ⅰ：有效区（数据易采集，读数稳定）Ⅱ：过渡区（视情况选用数据） Ⅲ：无效区（数据采集困难且读数不稳定）

4 结语

在常规电法勘探的方法理论和实际应用中，国内外许多研究者提出了各种校正方法，笔者在分析和研究前人已取得的成果基础上，我们得出了对称四极测深AB/2距探测的有效探测深度的变化可根据“H=K·arctg(（AB/2）/N)”反正切函数曲线进行修正，并建立了AB/2距的有效探测深度改算模型图，实际工作中使用时选好模型图中的具体曲线，就可对AB/2距的有效探测深度进行快速改算，就能更加有效地反映接近真实深度的信息来指导探矿工程的布设,从而提高电法勘探找矿效果。

[1] 蒋元安，等. 激电中梯勘探深度探讨[J]，西部探矿工程，2010, 10.

[2] 李杰, 等. 常规电法勘探探测深度物理模拟实验分析[D]. 中国地球物理学会第二十四届年会论文, 2008.

[3] 杨宏勇. 不均匀介质中定深度的方法技术[J]. 《地质与勘探》1996.

[4] 赵和云, 等. 地电阻率法中勘探深度和探测范围的理论讨论和计算[J]. 西北地震学报, 1982，01.

[5] 徐祖东. 沉降电极法—在低阻覆盖区提高激电法勘探深度的一种有效方法[J]. 矿产与地质. 1986年04期集》。

[6] 吴信民, 等. 论电法勘探的理论探测深度[J]. 东华理工大学学报(自然科学版)， 2013, 01.

[7] 樊伟宏, 等. 提高电法勘探深度的双二极垂直极化法[D]. 1992年中国地球物理学会第八届学术年会论文集，1992年.

[8] 闫述, 等. 华北型煤田水文地质电法勘探的深度问题[J]. 煤炭科学技术, 2006, 12.

[9] 李治时, 等. 电法找水效果[J]. 物探与化探, 1992, 8L

[10] 魏盎. 电测找水技术在哲盟山丘地区的应用[J]. 东北水利水电, 1993, 11.

[11] 丽红. 关于电测找水三个技术性问题的探讨[J]. 龙江水利科技. 2003. 3.

[12] 刘春华. 综合物探基岩找水技术研究，《山东水利》2003年第5、6期合刊。

[13] 何继善. 可控源音频大地电磁测法，1990，中南工业大学出版社。

[14] 樊映川. 高等数学讲议[M]. 高等教育出版社, 1964, 10, 1.

Calculating Model For Effective Detection Depth of Symmetric Four-Pole Sounding

QIN Fei1,2ZHAO Ming-liang1LI Qing-hua1TAO Lin1

(1-No. 403 Geological Team, BGEEMRSP, Emeishan, Sichuan 614200; 2-Chengdu University of Technology, Chengdu 610059)

Change in effective detection depth of symmetric quadrupole sounding with increase in AB/2 in the same test area is shown by a curve similar to the arctangent function. The curve functional expressionis H=K·arctg ((AB/2)/N). The initial segmentof the curve is a positive correlation curvewith increase in AB/2 distance, but the added value of the terminal tends to zero. Accordingly, a calculating model for effective detection depth of symmetric four-pole sounding is set up.

electrical sounding; four-pole sounding; AB/2 distance; calculating model of detection depth

2018-03-12

秦飞（1983-），男，四川峨眉人，物探工程师，成都理工大学地球物理学专业毕业，主要从事地球物理找矿工作

P631.3

A

1006-0995（2018）02-0325-03

10.3969/j.issn.1006-0995.2018.02.031