基于逻辑回归的高压并联电抗器过流误报警判别方法

, ， ，

(1.国网四川省电力公司成都供电公司，四川 成都 610041； 2.国网四川省电力公司电力科学研究院，四川 成都 610041)

0 引 言

并联电抗器，一般接在高压输电线的末端和地之间[1]，用于对输电线路进行无功补偿，对线路的分布电压进行有效控制，抑制工频过压[2-5]。然而，在电力系统实际运行中，高压并联电抗器过电流报警频繁发生，影响电力系统安全可靠运行。

工程经验表明，高压并联电抗器过流报警存在两方面的原因。一是由于受到电力系统运行方式的影响，高压并联电抗器连接点的电压超过了电抗器额定电压，导致流过电抗器的电流超过额定值，进而引发报警。这一类报警是真实报警。二是由于高压并联电抗器中电流测量装置出现了问题，导致误差增加，甚至出现错误的测量结果而引发报警。这一类报警其实是在电流并未超过有效值的情况下而出现的误报警。

为了区分高压并联电抗器是否存在过流误报警，现场往往需对电抗器和输电线路停电试验，判断器件测量误差是否合理。由于需停电操作，这种方法对电力系统的稳定运行和经济运行有很大影响。为此许多学者提出了基于数据的电气系统二次设备故障诊断方法。文献[6]提出一种基于站间协同信息的电子式互感器故障诊断方法，对两端互感器测量值比较分析进行故障定位。文献[7]通过分析互感器故障模式和一次系统电气量变化特点进行故障诊断。文献[8]通过建立电流观测器模型进行二次量异常故障在线识别。文献[9]通过分析牵引变电所多个互感器测量值之间的相关关系对二次量故障进行在线识别。然而，上述分析方法需要在二次侧获得测量值。对于高压并联电抗器过流报警，由于只可以得到报警信号而无法获取其有效电流值，所以以上方法都不适用。

为此，提出了一种基于逻辑(logistic)回归[10]的高压并联电抗器过流误报警判别方法。该方法通过电抗器过流报警发生概率与测量电压之间的关系来判断报警的真实性。该方法简单可行，计算量小，便于工程应用。

1 高压并联电抗器过流报警

以某线路一次接线图为例，如图1所示，L是并联在输电线路上的三相电抗器；PT是电压互感器，用于测量线路电压，将测量值上传并保存到数据采集与监控(SCADA)系统中；CT是电流互感器，用于测量流经L的电流值，该测量值通常不会被系统采集，只用于报警显示，当大于L的额定电流时，系统发出电流报警信号。

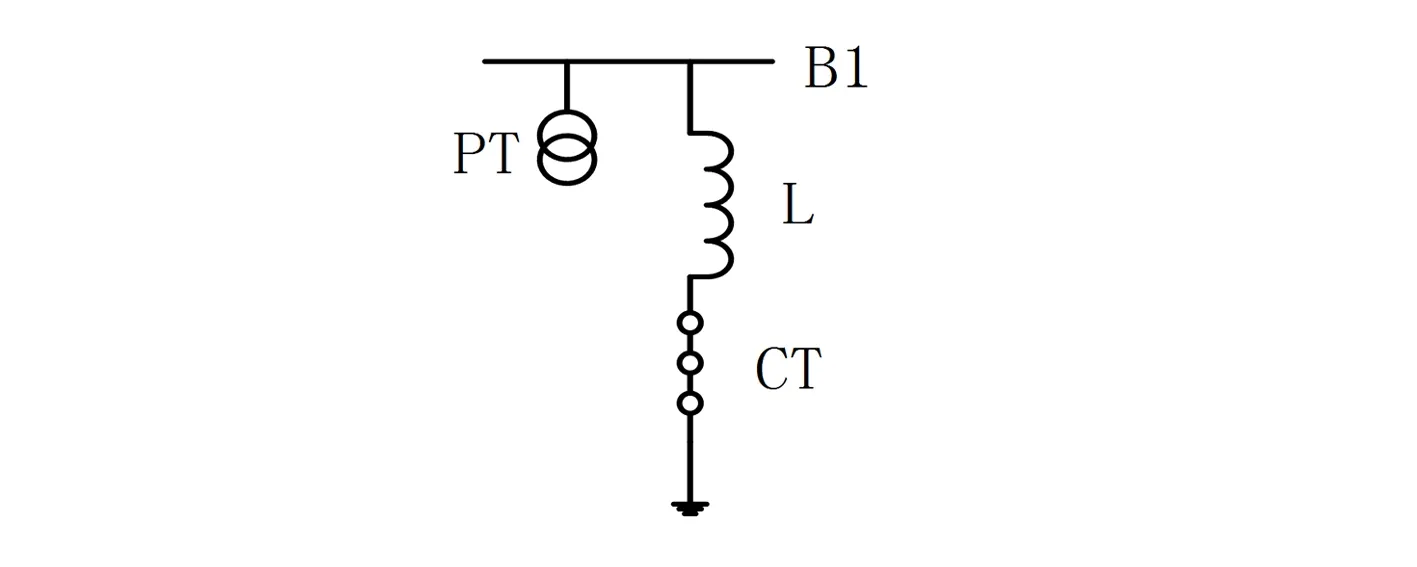
图1 某线路并联电抗接线

忽略设备精度及运行环境等因素的影响，UL和IL关系如式(1)所示：

(1)

式中：ω是相位差；L是电抗器的电感值。

可以看出，IL可由UL线性表示，当IL=IN时，UL=UN。根据系统报警的原理，当测量电压UL大于额定电压UN时，系统发出过流报警信号，其关系描述如式(2)：

(2)

其中，OC表示系统发出过流报警的逻辑值，当 OC=1时系统发出过流报警。设过流报警发生的概率为p，则p和测量电压UL之间的关系如图2所示。

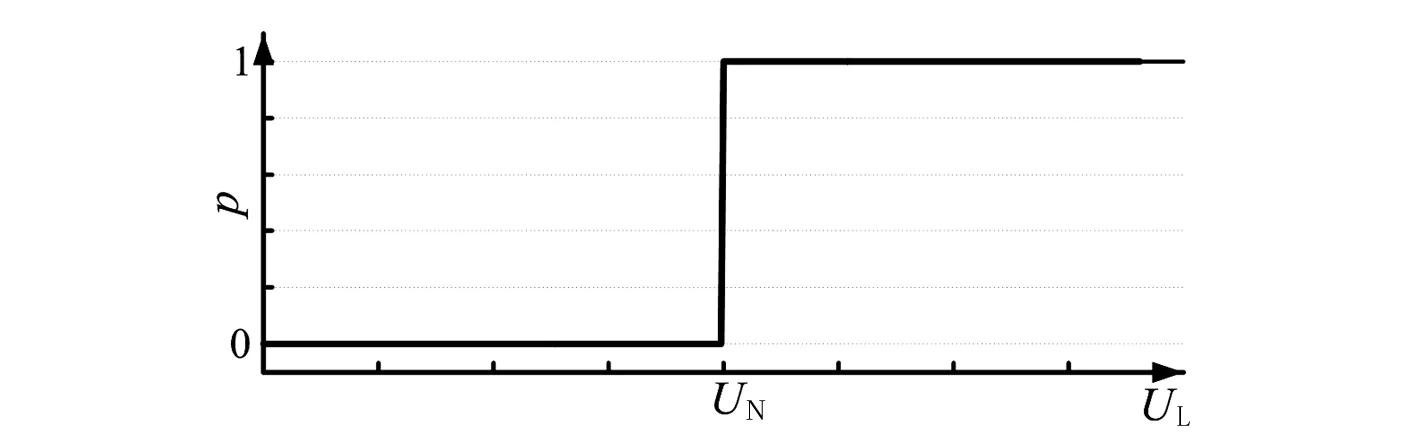
图2 无测量误差，过流报警发生概率与测量电压关系

考虑实测数据的测量误差，过流报警发生概率与测量电压之间的关系如图3所示。

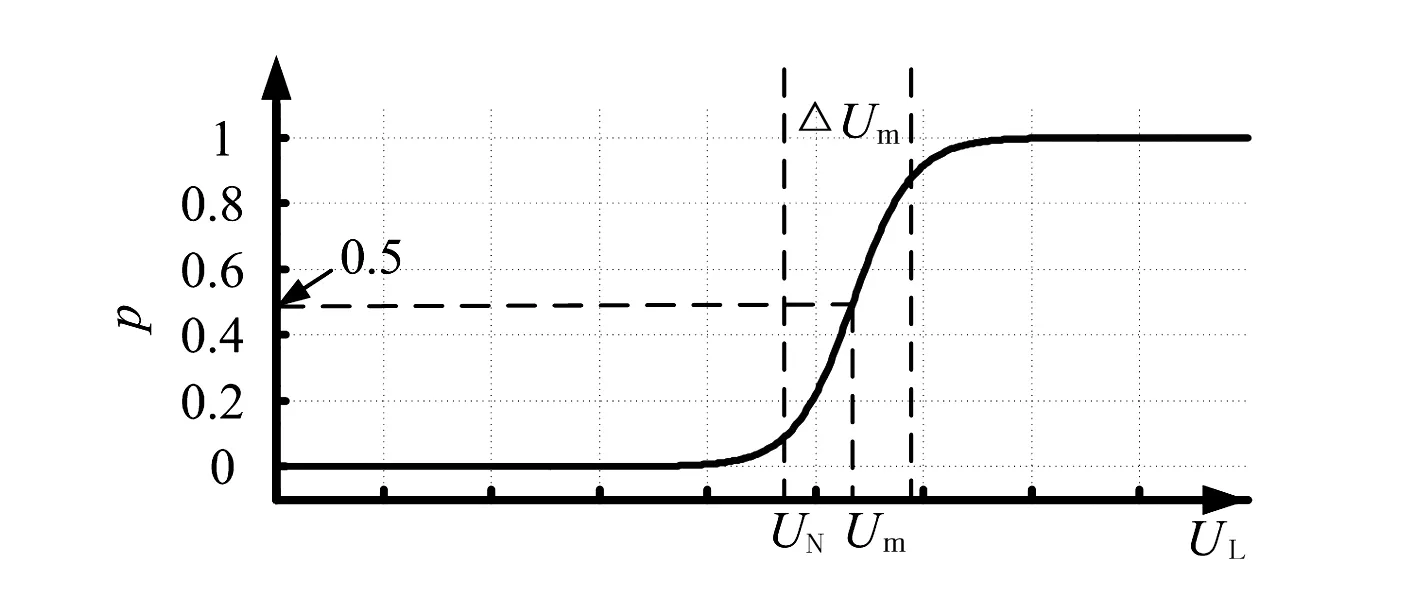
图3 有测量误差，过流报警发生概率与测量电压关系

对比图2和图3可以看出：

1)当测量误差为0时，p-UL关系曲线的中心点(即p=0.5对应的点)对应的电压为UN，曲线的不确定度ΔUm=0；

2)当测量误差不为0时，p-UL关系曲线中线点对应电压Um，且Um≠UN，此时，曲线的不确定度ΔUm>0。

在图3中，由于测量误差的存在，使得p-UL关系曲线中心点和不确定度发生改变，考虑对工业设备测量精度要求，电压互感器测量误差应不超过一定范围，通常要求其不大于0.5%，所以，互感器合理的测量值应满足式(3)关系：

(3)

式中，ΔUm为测量电压对应置信概率为90%的不确定度。

2 逻辑回归模型

逻辑回归模型常用于非线性统计分析，适用于二分类问题[11]。系统发生过流报警的概率为p，不发生的概率为1-p，对p/(1-p)作logit变换，以电压测量值为因变量，建立逻辑回归模型：

(4)

即：

(5)

式中：x为并联电抗器两端的测量电压；β0和β1为回归参数。通过式(1)和式(2)，可得到系统过流误报警判据如式(6)：

(6)

式中，pcon为置信概率，取pcon= 0.9。当两个判据任一个成立时，可认为电流报警为误报警。

3 过流误报警判别方法

建立高压并联电抗器过流报警发生概率与测量电压之间的逻辑回归模型，通过参数估计，利用上面定义的判据对过流报警进行判别，具体判别方法如下：

1)数据获取：从SCADA系统获取电抗器连接点的电压测量数据和对应时刻的过流报警信息，以分钟为时间间隔，取不同时间点的多组数据。

2)数据预处理：以1 kV为区间宽度，将获取的所有电压值划分在不同区间，例如[523.5,524.5)kV为其中一个电压区间，该区间内的电压值满足523.5≤U<524.5，在进行参数估时，区间电压值取区间左值523.5 kV。利用直方图统计各区间发生电流报警的概率p(Vi)：

(7)

式中：nV(Vi)为所取测量点映射到对应电压区间的数量；nOC(Vi)为电压测量值位于对应区间时，过电流报警发生的次数。

3)模型建立：建立过流报警发生概率p与测量电压Vi之间的逻辑回归模型。

4)参数估计及报警真实性判别：对回归系数β0和β1进行回归求解，并将结果代入式(6)进行判别。

4 算例分析

4.1 算例1 实测数据

以西南电网某500 kV输电线路中的某并联电抗器为例，利用一组实测数据对其过流报警真伪进行判别。该并联电抗的额定电压为525 kV，额定容量为120 MVA。在2017年7月，该设备发生过流报警17 973次。通过数据对比发现，其中有7100次报警发生时，测量电压小于额定电压。另外，当测量电压高于额定电压时，有6900次未出现报警。为此，怀疑相关测量环节出现问题。利用所提出的识别方法对此进行分析。从SCADA系统中获取该段时间的数据，并通过上面介绍的方法进行预处理后的统计情况见表1。

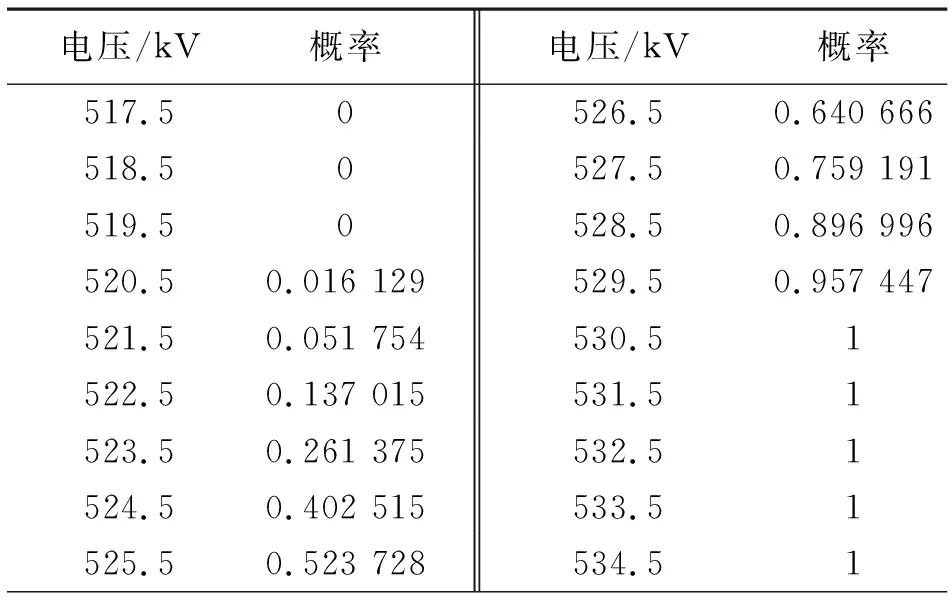
表1 算例一数据统计表

对表1的数据利用逻辑回归建模进行参数估计，获取参数β0和β1的值，得到式(8)。

(8)

将所得参数值代入两个判据：

(9)

(10)

由此可见，两个判据均不满足，可以认定该线路的并联电抗器7月报警情况属于正常报警。后续对该电抗器的电流测量等环节进行试验也表明设备正常，进一步验证了所提出的判别方法的有效性。

4.2 算例2仿真数据

在仿真环境下，将上面的并联电抗器精度允许偏差设为1%，获取了44 640个电压数据及报警信息。按照上面的方法进行预处理后得到表2数据。

表2 算例2数据统计表

同样，通过对逻辑回归模型进行参数估计，得到：

(11)

代入判据得：

(12)

(13)

可见，第2个判据成立，由此认定在仿真环境下，该高抗设备的过流报警存在误报警情况。

5 结 语

针对高压并联电抗器误报警情况，通过对报警概率和测量电压建立逻辑回归模型，并定义了误报警的判定准则。

1)基于逻辑回归的高压并联电抗器过流误报警方法是数据驱动的，避免了常规设备检测需要的停电试验，提高了设备缺陷识别的效率。

2)该方法只需要使用线路上的电压互感器有效测量值和并联电抗器的过流监测信号，不需要额外增加测量设备。结合工程实例，通过实例计算和仿真试验，取得了良好的效果。因此，该方法具有很好的实用性。

[1] 顾生杰, 田铭兴. 基于串联电容补偿的超/特高压输电线路可控并联电抗器补偿度分析[J]. 高电压技术, 2014, 40(6):1858-1863.

[2] 周沛洪，何慧雯，戴敏，等.可控高抗在1000 kV交流紧凑型输电线路中的应用[J]. 高电压技术，2011，37(8)：1832-1842.

[3] 陈水明, 王威, 杨鹏程. 限流电抗器对输电线路工频过电压的影响[J]. 电网技术, 2010, 34(3):193-196.

[4] 孟恒信, 梁建伟, 薛磊,等. 山西500 kV长久三回线路电流不平衡原因分析及改造研究[J]. 电网技术, 2013, 37(3):641-646.

[5] 郑涛, 赵彦杰. 超/特高压磁控式并联电抗器合闸过程分析及其影响研究[J]. 中国电机工程学报, 2015, 35(7):1790-1798.

[6] 熊小伏, 杨雪东, 刘年. 基于站间信息的电子式互感器故障协同诊断方法[J]. 电力系统保护与控制, 2012，40(21):80-83.

[7] 熊小伏, 何宁, 于军,等. 基于小波变换的数字化变电站电子式互感器突变性故障诊断方法[J]. 电网技术, 2010(7):181-185.

[8] 王洪斌，唐昆明，徐瑞林，等.数字化变电站电子式互感器源变性故障诊断方法形容[J].电力系统保护与控制，2012, 40(24):53-58.

[9] 李朝阳, 杨健维, 王玘,等. 基于主元分析的牵引变电所互感器二次量异常故障在线识别方法[J].电力自动化设备, 2015, 35(8):103-109.

[10] Xiong Y, Zuo R. GIS-based Rare Events Logistic Regression for Mineral Prospectivity Mapping[J].Computers & Geosciences, 2018，111(2)：18-25.

[10] 许冲, 戴福初, 徐素宁,等. 基于逻辑回归模型的汶川地震滑坡危险性评价与检验[J]. 水文地质工程地质, 2013, 40(3):98-104.