基于简化联邦CKF的INS/GNSS组合导航算法*
卢 航 郝顺义 沈 飞 李保军
空军工程大学航空航天工程学院, 西安710038
惯导系统利用惯性元件测得角速度和比力,通过积分进而获得导航参数,但由于陀螺和加计存在漂移,导航误差会随时间积累,因此需要高精度的飞行器进行导航[1]。GPS作为天基无线电导航系统的一种,具有定位和测速精度高,误差不随时间积累的特点,但当可见星数量不足时会影响导航精度,且其使用受制于人,不可完全依赖[2-4]。BDS作为我国自主研发的一套导航系统,可以提供载体高精度的位置、速度信息。因此,将INS、GPS和BDS各导航系统进行组合,可以在很大程度上提升组合导航性能。但是,组合后如何能够更好地利用各导航系统信息,形成一个高精度导航系统,是当前多传感器组合导航的主要研究任务之一。
利用卡尔曼滤波技术对导航误差参数做最优估计,其估计精度严重依赖所建模型的准确度。而在高精度多传感器组合导航系统中,模型阶数一般很高,且为非线性,所以在对导航信息进行融合处理时,优先考虑采用联邦卡尔曼滤波器(Federated Kalman Filter,FKF),而非集中卡尔曼滤波器。因为相比于联邦卡尔曼滤波器,集中卡尔曼滤波器虽然具有滤波精度高的优点,但其模型阶数高,计算量大,滤波器更易发散。此外,其容错性差,不利于故障诊断与隔离。联邦卡尔曼滤波器作为一种分散化滤波器,设计灵活、容错性能好,且在高精度多传感器组合导航中,针对高阶系统模型可以降低计算量,已被越来越广泛应用[5-6]。
传统的联邦卡尔曼滤波器要求主滤波器和各子滤波器的模型必须为线性,但组合导航系统模型的本质是非线性的,采用传统的联邦卡尔曼滤波需要对系统进行线性化,否则会影响系统的滤波性能[7]。针对这一问题,文献[8-9]提出粒子联邦滤波算法,用于多传感器组合导航系统,并取得了良好的效果,文献[10-11]提出了把UKF和联邦滤波结合,用以解决组合导航系统滤波中的非线性问题。
本文针对高精度多传感器组合导航中子系统模型为部分非线性,提出将简化的求容积卡尔曼滤波(Reduced Cubature Kalman Filter,RCKF)[12]融入到联邦滤波结构当中,并将滤波器应用于建立的INS/GPS/BDS紧组合模型进行仿真,仿真结果与联邦UKF和联邦CKF算法进行了对比,验证了论文提出算法的优势,取得了较好效果。
1 INS/GNSS联邦滤波器设计
1.1 子滤波器算法
考虑如下离散非线性系统:
xk=Φk,k-1xk-1+Γk-1wk-1
zk=h(xk)+vk
(1)
式中,Φk,k-1∈Rn×n为线性状态转移矩阵;Γk-1为系统噪声驱动阵;h(·)为非线性量测函数;系统状态向量:xk∈Rn;量测向量:zk∈Rm;wk-1和vk为互不相关的高斯白噪声,其方差分别为Qk-1和Rk。
1.1.1 标准容积卡尔曼滤波算法
考虑如下形式的多维高斯权重积分:
(2)
其中:f(x)为非线性函数,Rn为积分区域,一般情况下,上述积分无法获得解析解,需用数值积分方法得到其近似值,可选择一组具有权重值(wi,ξi)的点集来近似积分,即
(3)
CKF采用Spherical-Radial准则选取2n(n为状态维数)个具有相同权值的容积点(wi,ξi),计算方法见式(4),计算出容积点集后,可以通过时间更新和量测更新得到CKF滤波算法[13]。
计算容积点和权值:
(4)
式中,[1]=[I,-I];I为n维单位矩阵;[1]i表示取[1]第i列。
CKF计算步骤如下:
1)初始化
给定均值和协方差:
(5)
计算容积点ξi和相应权值wi。
2)时间更新
滤波协方差矩阵分解:
Sk-1=chol(Pk-1)
(6)
其中,chol{·}表示矩阵的Cholesky分解。
计算求积分点:
(7)
传播求积分点:
(8)
状态预测:
(9)
状态预测协方差
(10)
3)量测更新
矩阵分解:
Sk/k-1=chol(Pk/k-1)
(11)
计算求积分点:
(12)
求积点传播:
Zj,k/k-1=h(Xj,k/k-1)
(13)
量测预测值:
(14)
预测误差协方差:
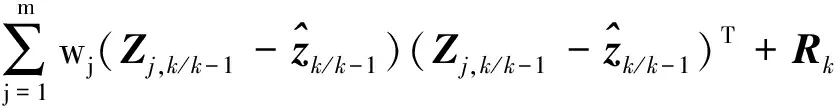
(15)
计算互协方差矩阵:
(16)
计算滤波增益:
(17)
状态更新:
(18)
状态协方差矩阵更新:
(19)
1.1.2 简化求容积卡尔曼滤波算法
考虑到系统的状态方程为线性,量测方程为非线性,可在时间更新环节用线性卡尔曼滤波对CKF进行简化,得到RCKF算法。在该环节中,标准CKF算法先要计算容积点和权值,后对滤波协方差矩阵进行Cholesky分解,再计算容积点、传播容积分点,最后根据权值计算状态预测值预测协方差阵。其中,式(4)用到的矩阵分解,其运算时间与状态维数紧密相关,大大增加了计算量。而相同过程,RCKF算法则避免了计算容积点以及协方差矩阵分解,直接用状态转移矩阵计算一步预测值。
通过上述说明可以给出该RCKF算法的实现流程如下:
1)时间更新
状态预测:
(20)
状态预测协方差阵:
(21)
2)量测更新
计算式(11)~(19),即可完成RCKF滤波算法。
1.2 联邦滤波器结构
联邦滤波器结构如图所示:
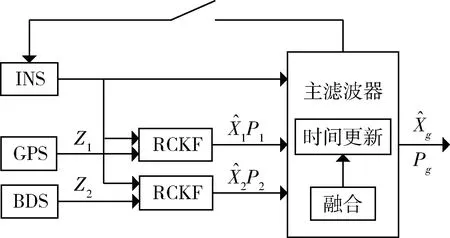
图1 联邦滤波器结构
本文建立的SINS/GNSS紧组合导航联邦滤波系统,将惯导系统设为公共参考系统,其输出信息和GPS、BDS信息构成子系统量测量。针对子系统模型为状态线性、量测非线性的问题,提出将RCKF的计算过程融入到联邦滤波结构框架中,构成一种新的简化联邦CKF滤波算法。相比于标准CKF算法,在时间更新过程中,RCKF算法状态转移矩阵计算一步预测和预测协方差矩阵,避免了采用求容积点近似计算的复杂过程及协方差矩阵分解,大大减少了计算量。
联邦滤波采用方差上届技术、信息分配方法使得各子滤波器估计状态可以按不相关的方式处理,具体算法流程如下:
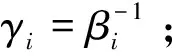
2)将主、子滤波器的过程噪声协方差阵按式(23)设置为组合系统过程噪声协方差阵的γi倍;
3)各子滤波器处理自己的量测信息,获得相应估计量;
4)在得到各子滤波器的局部估计和主滤波器的估计后按式(24)进行最优融合,得到主滤波器的滤波值和方差信息。
(22)
(23)
(24)
2 INS/GNSS组合联邦滤波模型
2.1 系统状态方程线性模型
组合导航误差状态方程如下[1]:
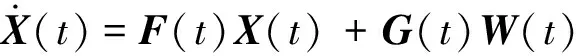
(25)
式中X(t)是22维误差状态向量,W(t)为系统噪声,G(t)为噪声分配阵,X(t)表示为:
X(t)=[φEφNφUδvEδvNδvUδLδλδhεbx
εbyεbzεrxεryεrzxyzδtGδtrGδtBδtrB]T
(26)
其中φE,φN和φU分别表示东、北、天向的失准角误差;δvE,δvN和δvU表示3个方向上的速度误差;δL,δλ和δh为位置误差;εbx,εby,εbz,εrx,εry,εrz,x,y和z分别表示陀螺常值漂移、相关漂移和加计零偏;δtG,δtB,δtrG和δtrB分别为GPS、BDS的时钟误差等效的距离误差,与时钟频率误差等效的距离误差。
2.2 INS/GNSS量测方程非线性模型
2.2.1 伪距量测方程
GPS和BDS使用同一量测模型,S卫星(S表示GPS或BDS)接收机测定的相对于第i(i=1,2,3,4)颗卫星的伪距值为:
(27)
式中:(x,y,z)表示载体在地球坐标系(ECEF)下的位置真值,(xsi,ysi,zsi)为第i颗卫星的位置,δts为与时钟误差等效的距离误差,vρi为接收机的伪距量测误差。
惯导系统以东北天地理坐标系作为导航坐标系,其所得的测量值是以纬度LI、经度λI和高度hI表示的,那么载体的真实位置为:L=LI-ΔL,λ=λI-Δλ,h=hI-Δh,将其转化到ECEF坐标系,转换关系如下:
(28)
式中,RN为卯酉圈主曲率半径;e为椭圆扁心率。同理,惯导解算位置在ECEF系坐标如下:
(29)
联合式(28)、(29)带入到式(27),可得伪距量测方程为:
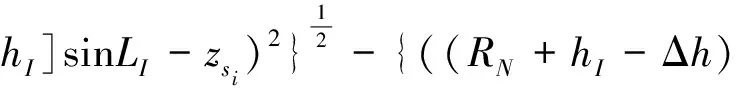
(30)
2.2.2 伪距率量测方程
S卫星接收机测定的相对于第i(i=1,2,3,4)颗卫星的伪距率为:
(31)
(32)
(33)
vE=vIE-δvE,vN=vIN-δvN,
vU=vIU-δvU
(34)
ECEF坐标系下惯导输出速度如下:
(35)
综上各式,可得到伪距率量测方程为:

(36)
根据式(30)和(36),可以得到卫星的非线性量测方程为:
(37)
3 仿真实验及分析
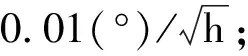
对比图2~3及表1中数据发现,联邦UKF(k=0)和联邦CKF对位置误差的估计精度相当,其原因在于两种确定性采样非线性滤波方法所捕获的均值和方差估计值都能达到泰勒展开式的三阶精度[14]。不过CKF使用2n个采样点,而UKF需2n+1个采样点,因此联邦CKF计算量小一些。此外,UKF需合理地调节各参数因子,才能选择出有效的sigma点,而CKF只需由式(4)便能得到容积点,其算法设计也更为简单。综上,针对本文所建模型,相比于联邦UKF,联邦CKF在保证滤波精度相当的情况下,在算法实现复杂度方面更具有优势。
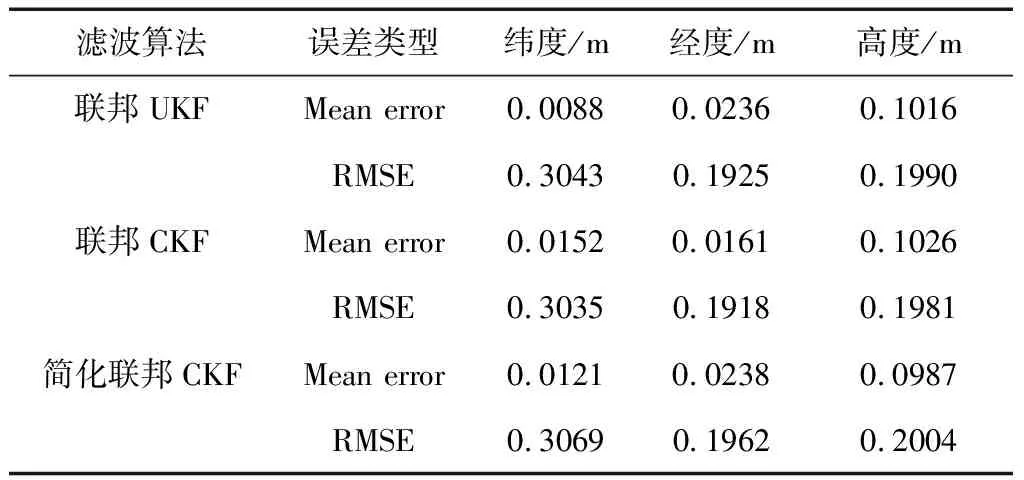
表1 定位误差比较
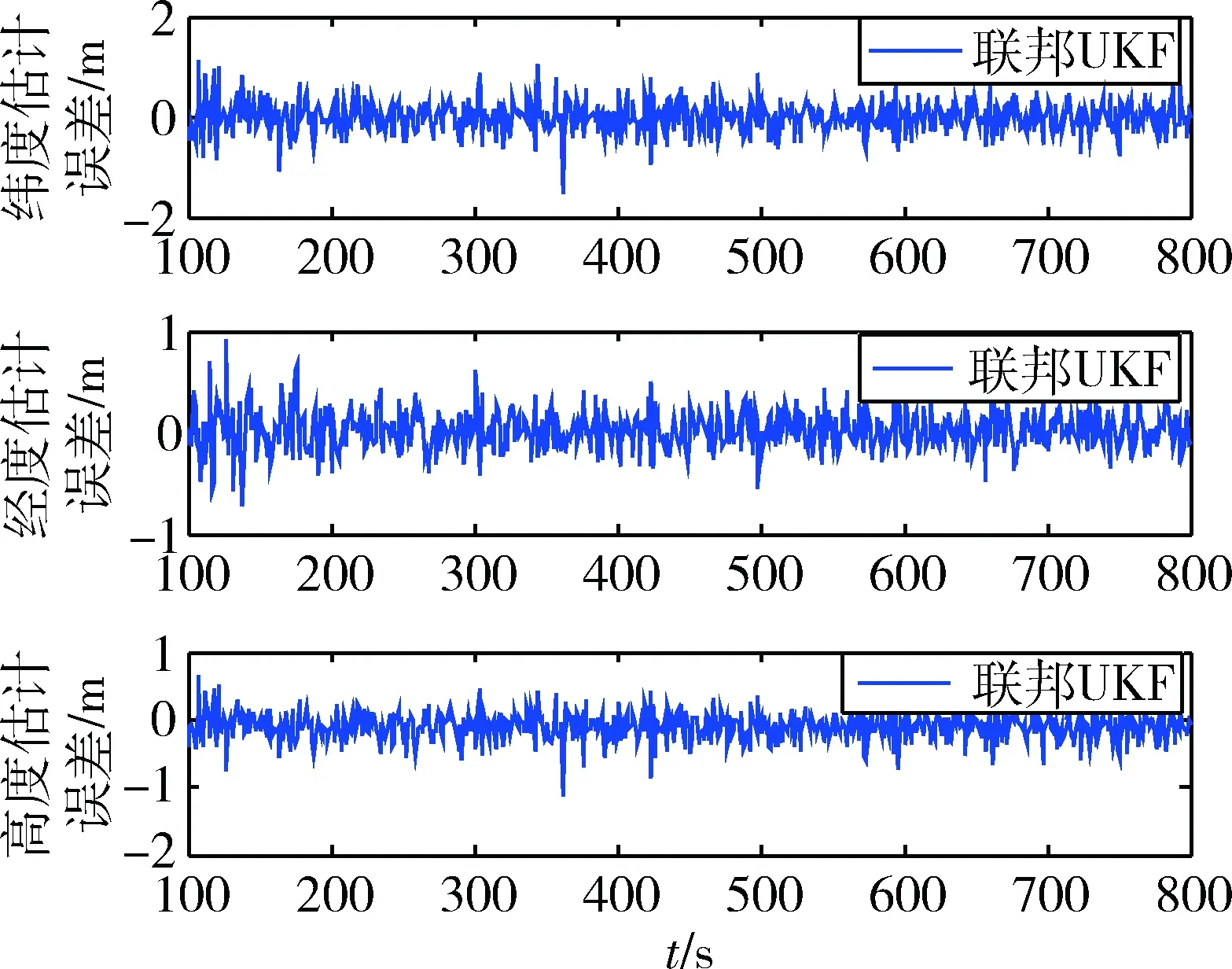
图2 联邦UKF定位误差
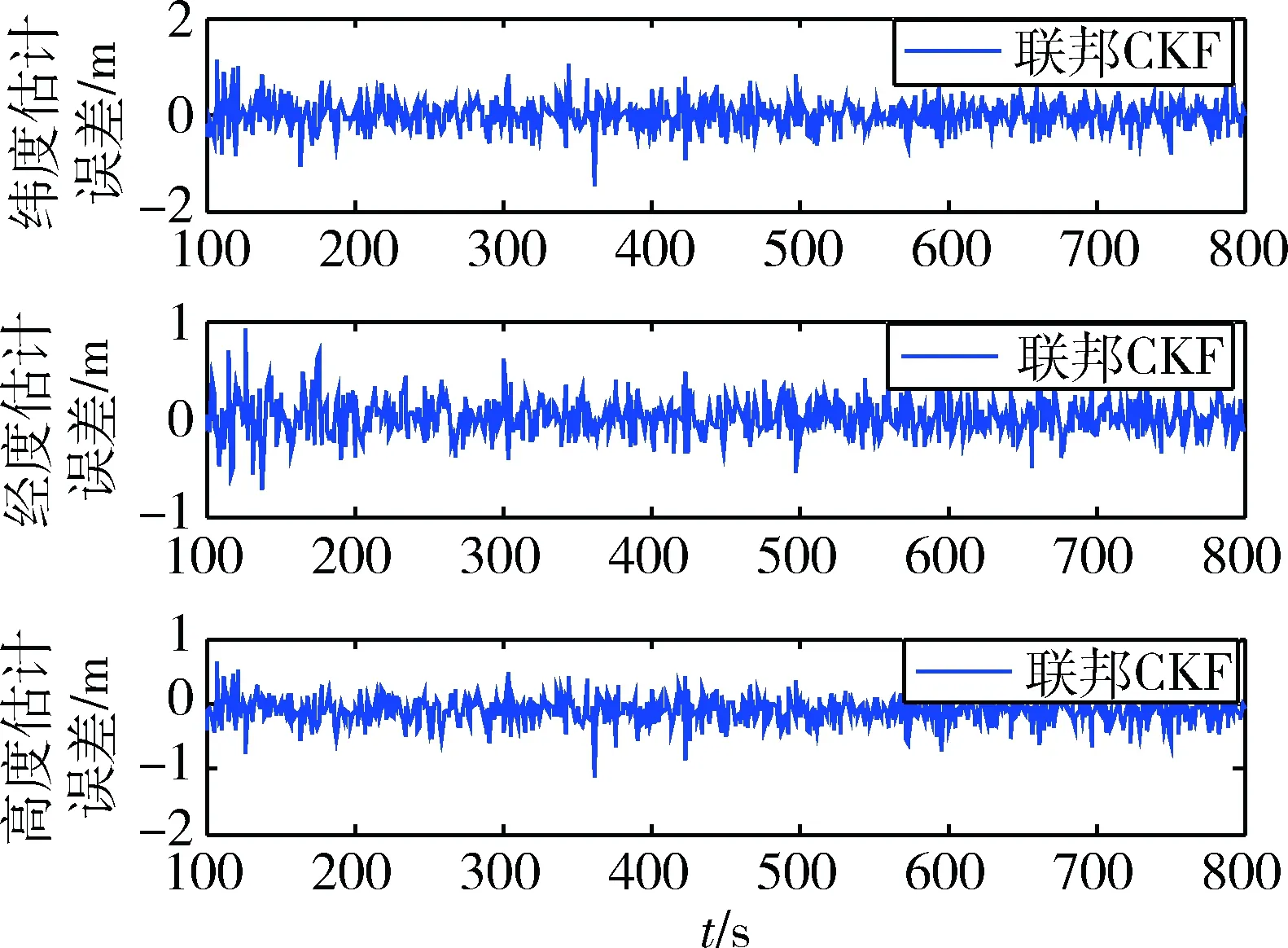
图3 联邦CKF定位误差

图4 简化联邦CKF定位误差
对比图3~4以及表1中数据发现,简化联邦CKF算法与联邦CKF算法位置误差估计精度相当。但在子滤波器时间更新过程中,联邦CKF算法先要计算容积点,后对滤波协方差矩阵进行Cholesky分解,再计算求积点、传播求积分点,最后根据权值计算状态预测值、以及预测协方差阵,其中,求取平方根矩阵用到的矩阵分解,其运算时间与状态维数紧密相关,大大增加了计算量。而同样过程,简化联邦CKF算法则避免了计算求积点以及协方差矩阵分解,直接用状态转移矩阵计算一步预测值,减小了运算成本。
将2种算法用在仿真环境为:Lenovo M4360 i3-3.4GHz CPU, 2G内存,Matlab R2009a 32位版本的计算机上进行仿真;得一次联邦CKF的滤波时间为0.004312s;一次简化联邦CKF的滤波时间为0.002339s。通过比较可知,简化联邦CKF算法的时间消耗减少了近46%。
4 结束语
由于滤波器对导航参数的估计精度严重依赖于建模准确度,所以在高精度组合导航中,系统模型阶数一般很高,且为非线性。但考虑到系统实时性,模型中状态方程阶数远高于量测方程,将状态方程线性化,建立了状态方程为线性、量测方程为非线性的系统模型,同时选用计算简单、设计灵活、容错性能好的联邦滤波器做状态估计。本文针对所建模型,提出了一种新的简化联邦CKF滤波算法,该算法将CKF的计算过程融入到联邦滤波结构框架中,针对子系统模型存在状态方程线性的问题,对算法的时间更新过程进行了简化,简化算法避免了计算求积点及协方差矩阵分解,直接用状态转移矩阵计算一步预测值,减小了运算成本。最后,通过仿真实验对本算法进行了验证,将结果与联邦UKF算法、联邦CKF算法进行对比。仿真结果表明,相比于联邦UKF和CKF算法,所提算法在保证滤波精度的情况下,有效减小了计算量,改善了组合导航系统的性能。
参 考 文 献
[1] 刘建业,曾庆化,赵伟,等. 导航系统理论与应用[M].西安:西北工业大学出版社,2010.
[2] Irokawa R, Ebinuma T. A Low-Cost Tightly Coupled GPS/INS for Small UAVs Augemented with Multiple GPS Antennas. 200935-44.
[3] Ali J, Mirza M. Performance for a low SINS/GPS [J].Nonlinear Dynamics, 2010, 61(3):491-502.
[4] Li Y, RIZOS C, J, et al. Sigma-point Kalman for Tightly Coupled GPS/INS Integration[J]. Journal of the Institute of Navigation, 2008, 55(3): 167-177.
[5] 张科,刘海鹏,李恒年,等. SINS/GPS/CNS组合导航联邦滤波算法[J].中国惯性技术学报, 2013, 21(2): 226-230.(Zhang Ke, Liu Haipeng, Li Hengnian, Qian Shan. SINS/GPS/CNS Integrated Navigation Federal Filtering Algorithm [J]. Journal of Chinese Inertial Technology, 2013, 21(2):226-230.)
[6] Carlson, N.A., Federated Filter for Distributed Navigation and Tracking Applications, Proc. ION 58th Annual Meeting, June 2002:340-353.
[7] A. Maier, S. Kiesel, G. F. Trommer. Performance Analysis of Federated Filter for SAR/TRN/GPS/INS Integration[J]. Gyroscopy and Navigation, 2011, 2(4):293-300.
[8] Aggarwal P, Syed Z, El-Sheimy N. Hybrid Extended Particle Filter(HEPF) for Integrated Cilvilian Navigation System.[C]//IEEE/ION Position, Location and Navigation Symposium, 2008:984-992.
[9] Lim Jaechan, Hong Daehyoung. Gaussian Particle Filtering Approach for Carrier Frequency Offset Estimation OFDM System[J]. IEEE Signal Processing Letters, 2013, 20(4):367-370.
[10] Hu H D, Huang X L. SINS/CNS/GPS Integrated Navigation Algorithm Based on UKF[J]. Journal of Systems Engineering and Electronics, 2010, 21(1):102-109.
[11] 李丹,刘建业,熊智,等. 应用联邦自适应UKF的卫星多传感器数据融合[J].应用科学学报, 2009, 27(4): 359-364.(Li Dan, Liu Jianye. Xiong Zhi, Yu Feng. Multi-sensor Data Fusion for Satellite Based on Federate Adaptive Unscented Kalman Filter [J]. Journal of Applied Sciences, 2009, 27(4):359-364.)
[12] Mohammed D, Abdelkrim M, Mokhtar K, Abdelziz O. Reduced Cubature Kalman Applied to Target Tracking [C]//The 2nd International Conference Control, Instrumentation and Automation (ICCIA), Shiraz: IEEE, 2011: 1097-1101.
[13] Arasaratnam I, Haykin S. Cubature Kalman Filter[J]. IEEE Trans on Automatic Control, 2009, 54(6): 1254-1269.
[14] 孙枫,唐李军.基于Cubature Kalman Filter的INS/GPS组合导航滤波算法[J].控制与决策, 2012, 27(7): 1032-1036.(Sun Feng, Tang Lijun. INS/GPS Integrated Navigation Filter Algorithm Based on Cubature Kalman Filter [J]. Control and Decision, 2012, 27(7): 1032-1036.)

