高速公路桥梁挖孔灌注桩桩基控制爆破施工安全距离的确定

■廖大刚

（福建省交通科学技术研究所，福州 350004）

0 引言

工程施工经常会运用爆破的方法，这能极大程度地提高施工效率，为施工带来便利。但爆破施工往往也会带来一定的有害效应，例如爆破振动、空气冲击波、爆破飞石、噪声和粉尘，这些当中爆破振动是公认的爆破有害效应之首，其虽然产生于岩体的弹性震动范围区内，不会造成爆区周围保护物的地基岩石破坏，但它会使得保护物产生倾斜、破坏甚至倒塌，当振动频率达到或接近保护物的自振频率时，振动对保护物的影响就愈大。因此，有必要对爆破振动进行控制。其中最有效的方法就是使保护物位于爆破安全距离以外。所谓爆破安全距离即在爆破有害效应的影响时能保证保护物安全的前提下，爆源与保护物之间的距离。故爆破安全距离的确定显得尤为重要。

关于爆破安全距离的确定研究，张亚宾等[1]在爆破振动监测的基础上，结合数值模拟技术，研究了露天边坡爆破安全距离的确定。赵丰等[2]基于已有的爆破振动速度衰减模型及有限元模拟结果，研究了新建铁路隧道上跨既有公路隧道时控制爆破安全距离的确定。张涛等[3]借助于围岩中地震波传播速度解析解，研究了隧道掘进爆破振动作用下支护结构的安全距离。叶洲元等[4]基于现场监测数据建立了爆破振动安全距离计算优化模型，并编写了Visual Basic语言计算程序，结合实例探讨了某土石方爆破安全距离的确定。本文主要讨论通过萨道夫斯基公式反演计算的方法确定桥梁桩基爆破施工的安全距离。

1 基本原理

1.1 地震波的产生及其表示

炸药引爆后会形成压力突变、能量极高、破坏能力极强的冲击波，其强烈地冲击炸药周围的岩体，能够直接将

式中：V为质点峰值振动速速，cm/s；Q为装药量 （齐发爆破时为单次总药量，微差爆破时为单段最大装药量），kg；R为测点与爆源中心的距离；K、α为与地质条件有关的衰减指数。

1.2 监测原理

采用爆破测振仪对地震波进行采集，其基于电测法的原理。电测法的要点是利用敏感元件在磁场中的相对运动，产生与地震具有一定比例关系的电信号，从而将地岩层压碎，从而产生粉碎圈并使得冲击波能量大幅降低，导致冲击波衰变为应力波。应力波只能引起岩层产生裂隙，继而形成裂隙圈[5]。当应力波通过裂隙圈时，大部分能量被用于裂隙的起裂、扩展引起其强度大幅度衰减，大约在距离炮孔中心150倍炮孔半径以外时，应力波再也不能引起岩石的破裂而只能引起岩石质点的弹性振动，造成地面震动，即为地震波效应[6]。当地震波效应严重时，可能对周围构建物造成安全隐患。

通常，可采用爆破振动速度、加速度、位移、频率、持续时间等参量来衡量地震波的振动强度。国内外诸多学者认为，爆破振动速度相比于其他几个参数，与岩体性质有较稳定的关系，更能排除岩土因素的影响，且振速与结构的破坏特征关系较密切，故宜采用振动速度作为地震波 强 度 的 衡 量 标 准[7]～[10]。

研究和实践表明，爆破振动速度与炸药量、爆心距、地质地形条件、装药结构等因素有关[11]，常采用经验公式表示。传统的振动速度经验公式为前苏联M·A萨道夫斯基提出的萨氏公式[12]：震波在介质中的振动信号转换为电学量，然后对电学量进行测量，最终反算得到所要测量的地震波强度。

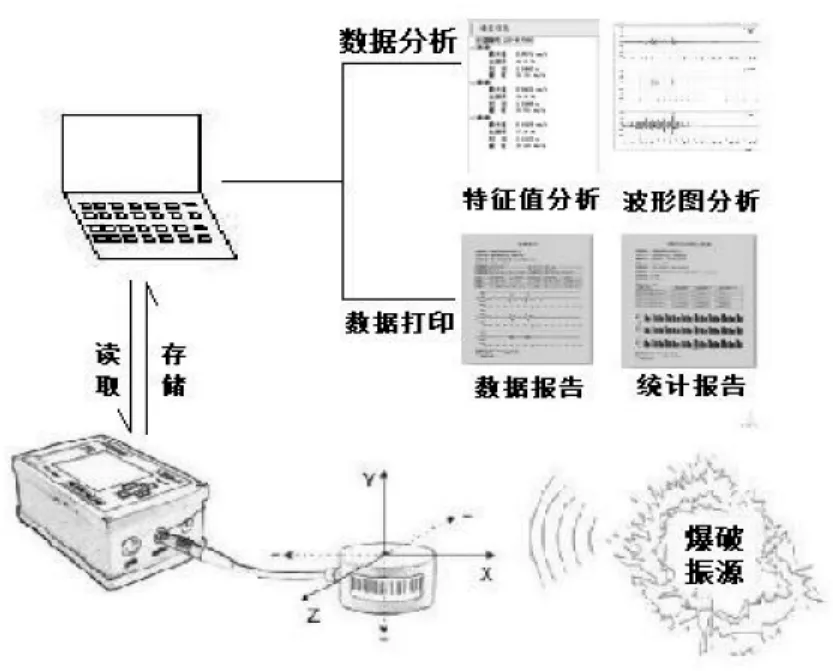
图1 爆破振动监测系统图

1.3 数据处理原理及安全距离的计算

对于监测数据的处理，一般采用基于最小二乘法原理的线性回归分析方法。

设有一组监测数据：(x1,y1)、(x2,y2)…(xn,yn)，若其满足回归方程y=kx+b，那么根据数理统计最大似然估计法，当对所有监测数据，令最小时，即可取得最优的线性回归方程。

要求得的最小值，由求最值的条件可知，需要满足：

即需要满足：

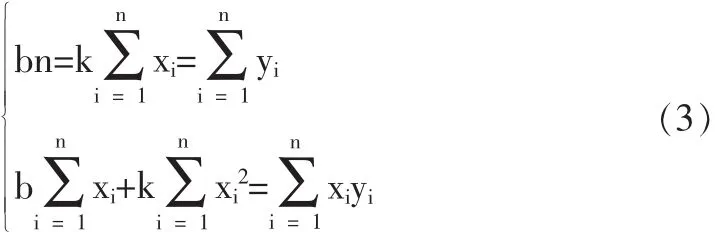
由上式可解得待定系数k、b的最大似然估计值为：

对式（1）两边取对数，可得：

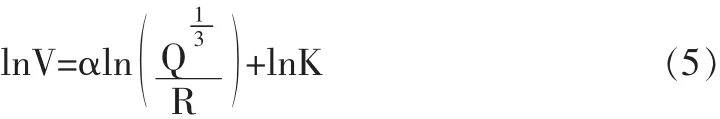
在式（5）的基础上，令，结合式（2～4）可得：

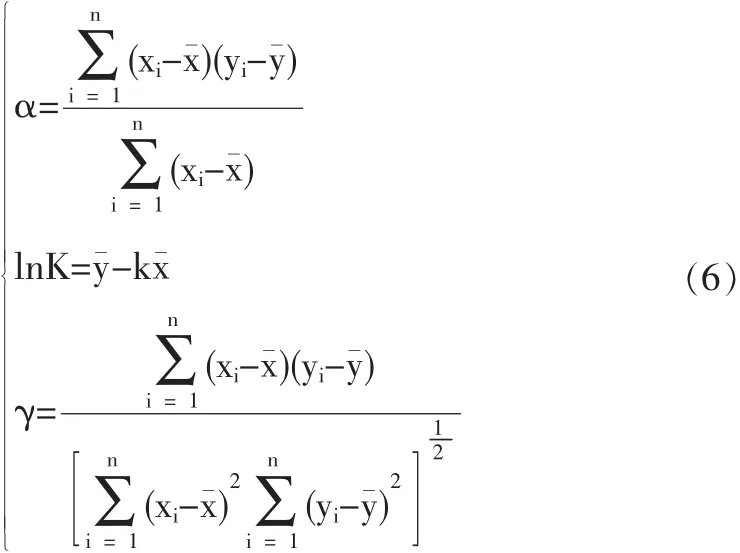
至此可以得到萨氏公式的各个待定系数，亦即完成了萨氏公式的拟合。在此基础上，若给定最大允许振动速度，则可以反演计算得到爆破安全距离：

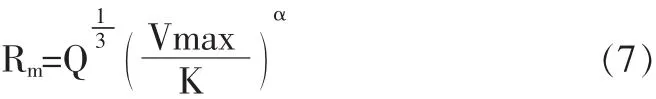
2 工程实例

2.1 工程概况

某高速公路桥梁桩基为挖孔灌注桩，实施浅孔爆破作业，最大药量为14kg。施工所在地地表为沉积砂土，浅层为砂岩，中部为较硬花岗岩，深部为坚硬花岗岩。爆区周边环境为：在爆区北侧有一条村道，沿村道两侧分布有居民房，均属于一般民用建筑物（砖房），最近的房屋与桩基的距离约为30m；村道北侧有一变电箱及数根高压线杆，如图2所示。为了解爆点的作业影响范围，进一步为指导施工方案的修正、控制和优化提供科学依据，本次试验通过快速、准确监测质点振动强度，拟合得到地震波传播的衰减规律，最终反演计算得到爆源的安全距离。

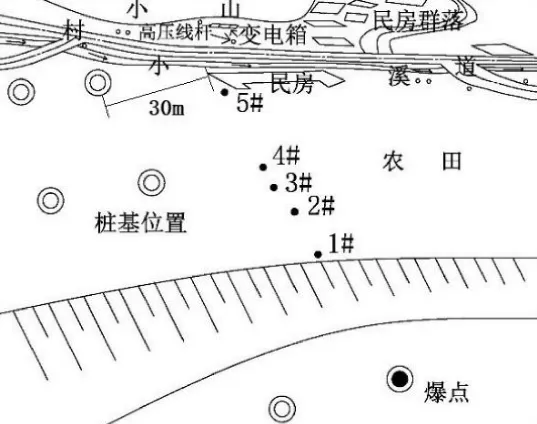
图2 测点布置平面图

2.2 测点布置

针对工程特点和居民房屋的分布情况，监测点的布置选在了较为开阔的荒废农田上。监测过程采用了5套成都交博科技有限公司生产的L20-N型智能爆破测振仪，设备采样频率为10k，触发电平设置为0.03cm/s，采样长度为4s。测点平面布置图如图2所示。

2.3 监测结果

因试验条件有限，仅进行了一次爆破振动的测试，共取得4组振动数据，列于表1中（其中4#测点的仪器未受触发）。同时，受篇幅所限，仅给出2#测点的振动波形图，如图3所示（图中横轴表示时间s，纵轴表示振幅 cm/s）。

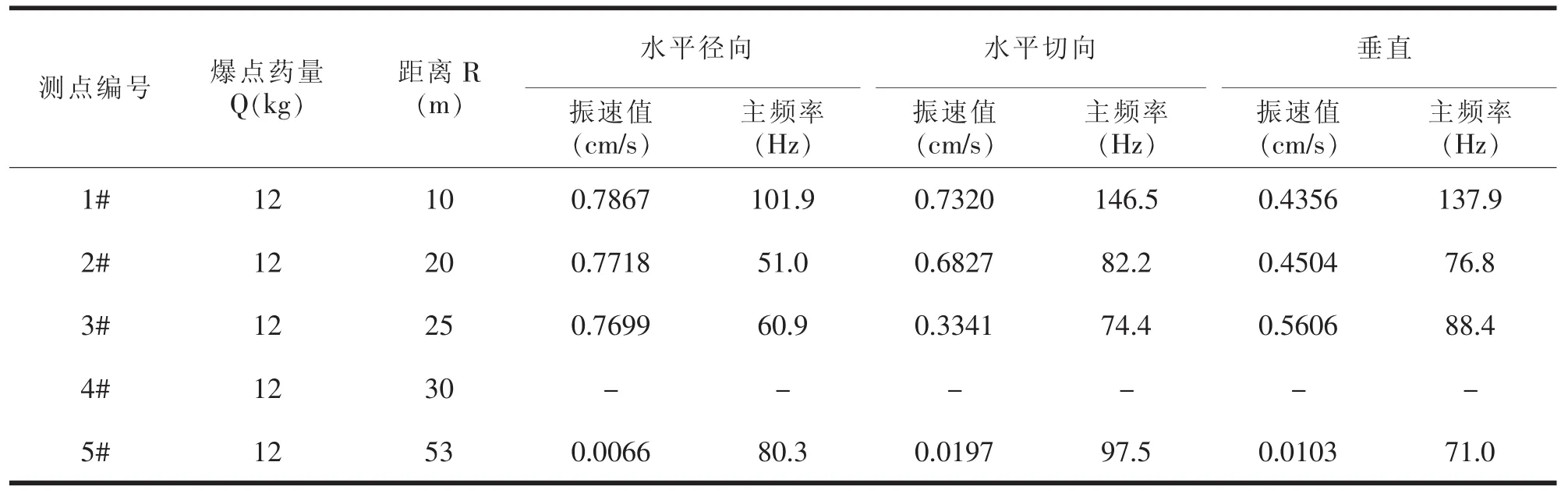
表1 测振数据表

图3 典型爆破振动速度波形图

2.4 结果分析

2.4.1 萨氏公式回归分析

根据监测数据结果及数据处理原理，可得到本次监测岩体中地震波的传播规律：

（1）水平径向质点振动速度回归结果如图4所示，其中 K=167.74，α=2.86，γ=0.822振动速度衰减规律为：

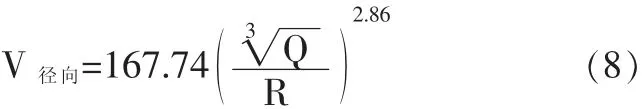
（2）水平切向质点振动速度回归结果如图5所示，其中 K=38.84，α=2.21，γ=0.916，振动速度衰减规律为：

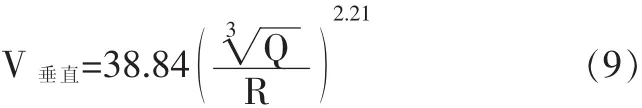
（3）垂直质点振动速度回归结果如图6所示，其中K=03.45，α=2.23，γ=0.851，振动速度衰减规律为：

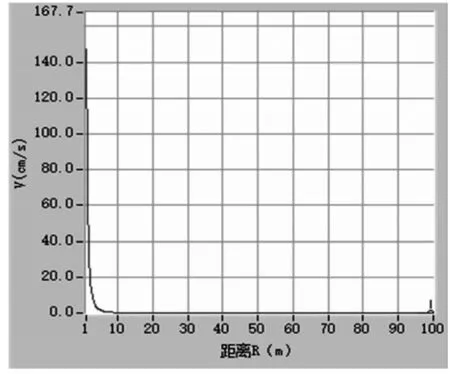
图4 V径向回归曲线

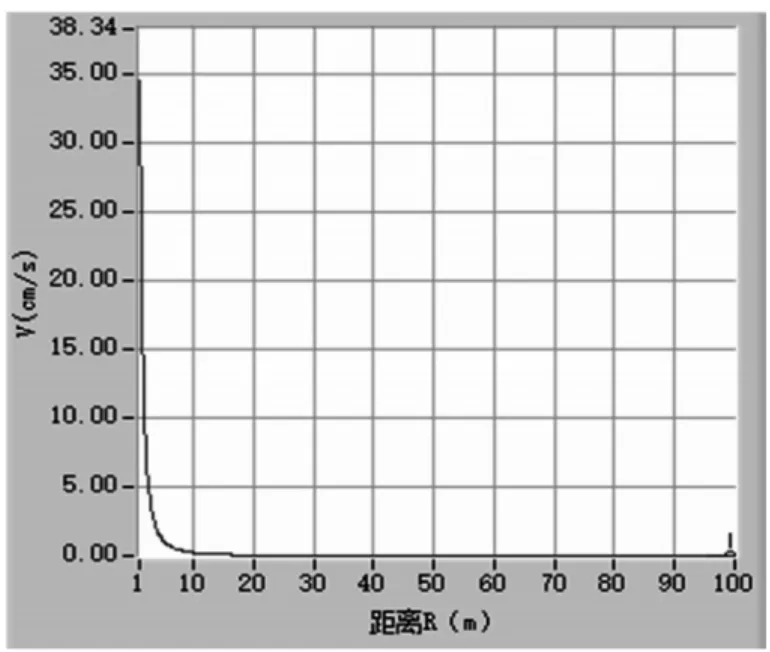
图5 V切向回归曲线

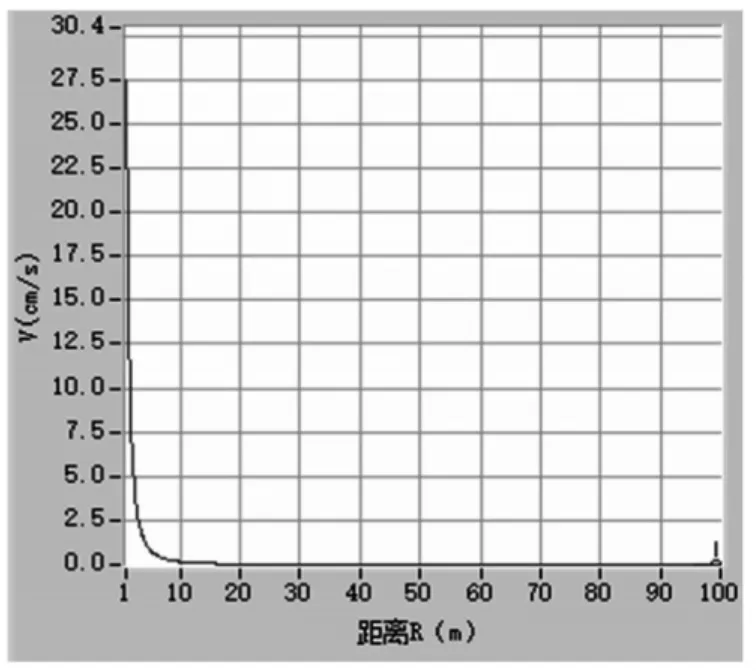
图6 V垂直回归曲线

2.4.2 安全距离分析

根据《爆破安全规程》（GB6722-2014）[13]，结合现场实测振动主频率，确定最大允许振动速度为2.0cm/s。由式（7）可计算得到不同药量下的安全距离，如表2所示。

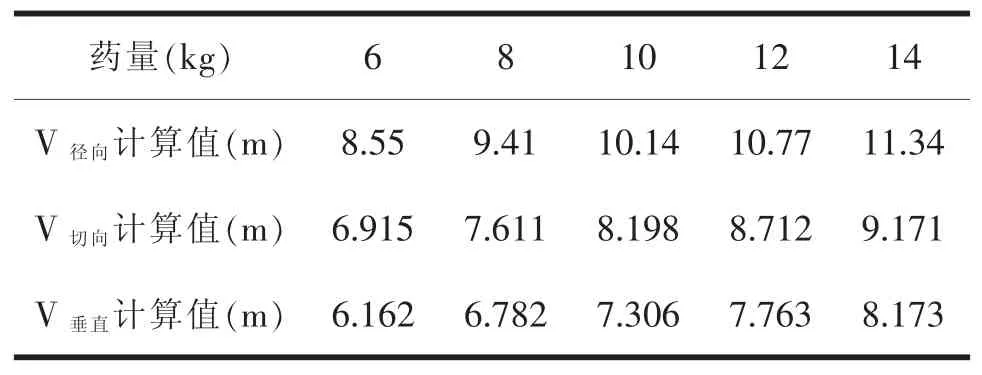
表2 爆破安全距离计算表

3 结语

（1）通过拟合地震波传播的衰减规律从而反演计算爆破安全距离，可得到水平径向、水平切向、垂直方向上的三种结果，应以三者中的最大值作为参考值。

（2）因爆破现场的复杂性及诸多因素的不确定性，建议实际工程中按计算结果的1.1～1.5倍取值。

（3）《爆破安全规程》（GB6722-2014） 给出了爆区不同岩性的 、的取值，可在无试验数据的条件下参考，若盲目按此数据类比取值是不客观的，会造成爆破安全距离的计算误差，利用监测数据拟合得到的 、值能在一定程度上减小误差。

（4）因试验条件有限，试验取得的振动数据较少，导致各向质点振动速度拟合中相关系数较小，回归结果稍有欠缺。今后类似工程爆破安全距离的确定，可按本文方法，增加试验次数进一步完善。

[1]张亚宾，张云鹏，陈超.爆破动载作用下边坡临界振速及安全距离的计算[J].金属矿山，2016，45（2）：137-140.

[2]赵丰，薛亚东，李硕标，等.新建铁路隧道上跨既有公路隧道控制爆破安全距离研究[J].铁道科学与工程学报，2016，13（7）：1365-1371.

[3]张涛，陈士海，张伟，等.掘进爆破振动作用下支护结构的安全距离[J].爆破，2014，31（1）：133-137.

[4]叶洲元，周志华.爆破震动安全距离的优化计算[J].中国安全科学学报，2005，15（3）：57-60.

[5]卢文波，岩石爆破中应力波的传播及其效应研究[D].武汉：武汉水利电力大学，1994.

[6]戴俊.岩石动力学特性与爆破理论（第2版）[M].北京：冶金工业出版社，2013.

[7]Berta Giogio.Blasting-induced vibration in tunneling[J].Tunneling and underground space technology，1994（2）：35-47.

[8]S.D.Butt，D.B.Apel，P.N.Calder.Analysis of High Frequency Microseismicity Recorded Geophsics at an Underground Hard Rock Mine[J].Pure and Applied Geophysics，1997，150（3）：693-704.

[9]宋光明，陈寿如，史秀志，等.露天矿边坡振动监测与评价方法的研究[J].有色金属，2000，4（7）：24～27.

[10]石崇，毕卫国.爆破地震破坏判据的探讨[J].岩土力学，2004，25（s1）：115-118.

[11]陈秋松，张钦礼，陈新，等.基于GRA-GEP的爆破峰值速度预测[J].中南大学学报（自然科学版），2016，47（7）：2441-2447.

[12]李洪涛，卢文波，舒大强，等.爆破地震波的能量衰减规律研究[J].岩石力学与工程学报，2010，29（s1）：3364-3369.

[13]中华人民共和国国家标准编写组.GB6722-2014，爆破安全规程[S].北京：北京标准出版社，2014.