核加速遗传算法求解折扣{0-1}背包问题
杨 洋,潘大志,贺毅朝
(1.西华师范大学 数学与信息学院,四川 南充 637009;2.河北地质大学 信息工程学院,河北 石家庄 050031)
0 引言
折扣{0-1}背包问题(D{0-1}KP)是经典0-1背包问题的一个扩展形式[1-5],其思想源于商业领域的打折,在项目决策、投资和预算控制等方面具有广阔的应用背景[3]。Guder和Guldan首先提出了单目标及多目标的D{0-1}KP,并实现问题求解[1-2]。后面大部分文献针对D{0-1}KP都是在精确算法或进化算法的基础,提出改进算法实现求解[3-5,10-11]。
文献[3]和文献[4]在利用遗传算法求解的过程中,交叉和变算子让本来已经选择且应该选择的物品被舍弃,使得D{0-1}KP较难得到最优解。而对于核算法,尤其是对于大规模实例时,求解速度比较缓慢。针对遗传算法和核算法单独处理D{0-1}KP时均较难快速取得较优解甚至最优解的问题,本文在现有GROA修复算法的基础上[4],将核算法[3]融合到遗传算法,得到核加速遗传算法(CEGA)。该算法通过计算得到精准核,将遗传算法的交叉和变异操作限定在核内进行操作,再用GROA对编码进行修复,以达到加速问题求解、提高求解质量的目的。
1 D{0-1}KP定义及数学模型
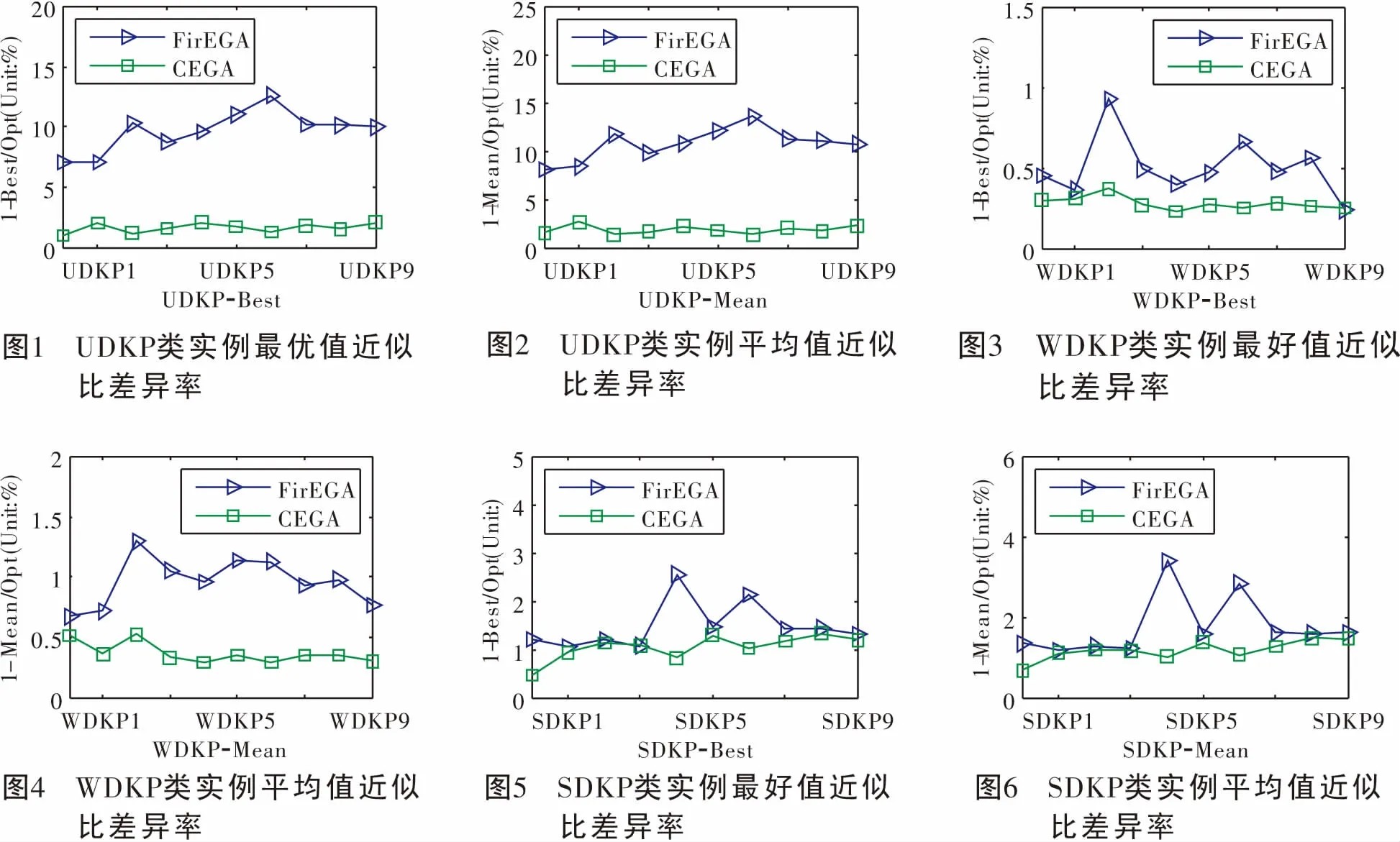
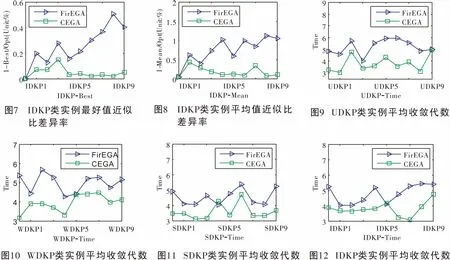
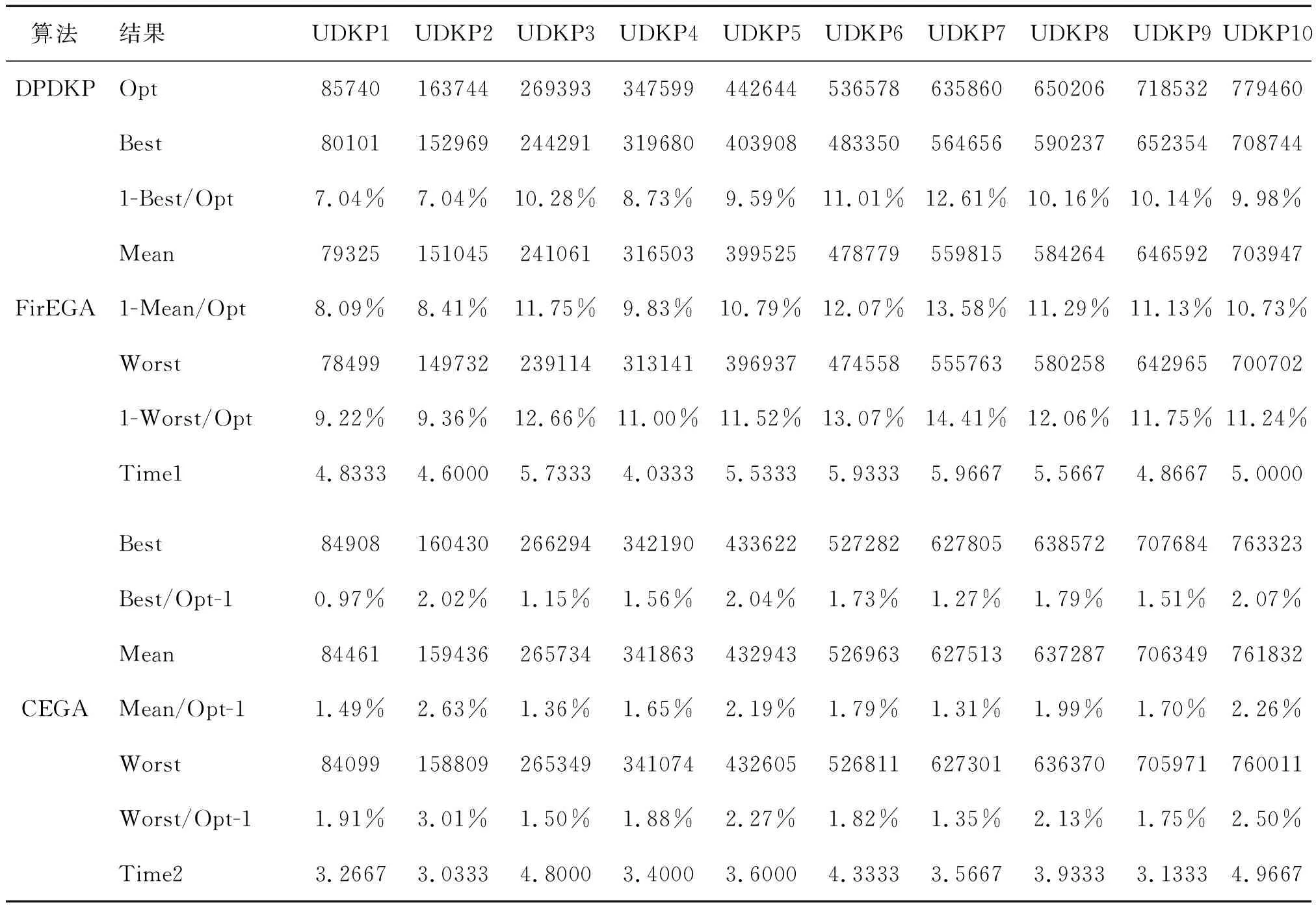
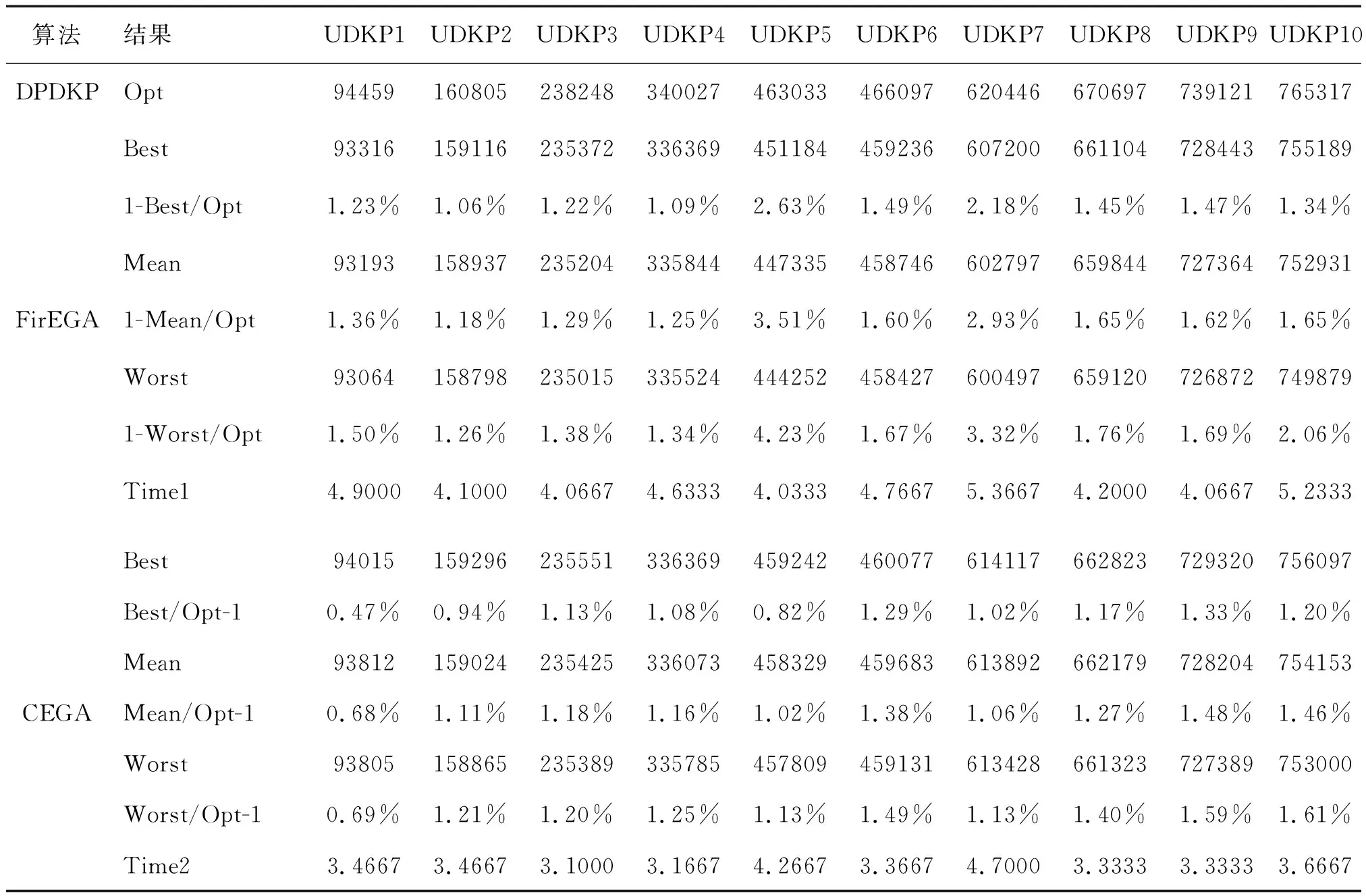
定义1:记D{0-1}KP的规模为项的个数3n,则规模为3n的D{0-1}KP实例由价值系数P={{p3i,p3i+1,p3i+2}|0in-1}、重量系数W={{w3i,w3i+1,w3i+2}|0in-1}和背包载重C构成,其中p3i+2=p3i+p3i+1,w3i+2 (1) s.t.x3i+x3i+1+x3i+21,i=0,1,…,n-1 (2) (3) x3i,x3i+1,x3i+2∈{0,1},i=0,1,…,n-1 (4) 其中,二元变量xj(0j3n-1)表示项j是否被装入背包中。显然,任意的0-1向量X=[x0,x1,…,x3n-1]∈{0,1}3n仅仅表示D{0-1}KP的一个潜在解,只有当它同时满足了约束条件(2)和(3)时才是一个可行解[3]。 核算法求解背包问题,是Balas和Zemel[14]为缩小求解问题规模于1980年提出的一种方法。该方法首先找出问题所有物品集的一个子集,作为问题对映的“核”,然后对核内物品进行取舍的搜索,达到加速求解问题的效果。实践证明,利用核算法能够有效加速小规模问题的求解[15]。但理论上求解背包问题的核对应的时间复杂度与求解该问题本身的时间复杂度相当,而D{0-1}KP是一个NP-hard问题,因此,对于大规模D{0-1}KP,利用核算法求解其时间复杂度也很大,问题仍然较难快速求解。 首先,对任意{0-1}KP的“精准核”C可以表述为: (5) 其中布尔集合X={x1,x2,…,xn}表示为该背包问题的最优解,xi=0表示第i个物品不选取,xi=1表示第i个物品选取;N是将物品按照价值密度进行排序后的集合。 对于D{0-1}KP,其核的求解与(5)式相同。但因D{0-1}KP每个项集中仅能选取一个项,则对于任意D{0-1}KP的布尔项集集合X,需满足条件(2)和(3),求解核的算法描述如算法1。 算法1 Core 输入:价值密度排序后价值向量P和质量向量W,背包容量C,参数N 输出:C=[s,t] 1.FORi←1TO3n 2.IFk+wSi 3.k←k+wSi; 4.X(i)←1; 5.END IF 6.END FOR 7.FORi←1TO3n 8.IFX(i)~=0 9.s←i; 10.BREAK; 11.END IF 12.END FOR 13.FORi←1TO3nDO 14.IFX(3n+1-i)=0 15.t←i; 16.BREAK; 17.END IF 18.END FOR 遗传算法[8-11](Genetic Algorithms,GA)是一种借鉴“适者生存”这一理念的演化算法,通过模拟生物种群增殖过程中的遗传变异过程,进行问题求解,在生产调度、图像处理等领域[12]应用广泛。对于传统遗传算法中三类算子具体内容可参考文献[9,13],对于利用EGA求解D{0-1}KP相关内容,具体可参考文献[4],本文限于篇幅,不再赘述。 为方便算法描述,设“S[0,1,…,3n-1]←Density({pj/wj|pj∈P,wj∈W,0j3n-1})”表示对所有的项(设有3n个项)按照价值密度即pj/wj(0j3n-1)的比值大小,从大到小进行排序并存入数组S中。 利用核算法的特点,得到精准核后,主要是将遗传算法的交叉算子、变异算子和选择算子的操作范围限定在精准核进行问题处理,从而减少无效操作并加速算法收敛。这里将融合核算法的遗传算法记为核加速遗传算法(CEGA),其算法步骤如算法2。 算法2 CEGA. 输入:价值向量P和质量向量W,背包容量C,参数N,遗传交叉变异算子Pc和Pm,最大迭代次数MaxIt 输出:近似最优解B(t)及近似背包价值量f(B(t)) 1.S[0,1,…,3n-1]←Density({pj/wj|pj∈P,wj∈W,0j3n-1}); 2.Randomly generate populationP(0)={Xi(0)|1iN}; 3.FORi←1TON 4.(Xi(0),f(Xi(0)))←GROA(Xi(0),S); 5.END FOR 6.DetermineB(0)byf(Xi(0))(1iN)inP(0);t←0; 7.WHILE(tMaxIt) 8.P1(t)←CRO(Core(P(t)),pc); 9.P2(t)←MUO(Core(P1(t)),pm); 10.FORi←1TONDO 11.(Zi(t),f(Zi(t)))←GROA(Zi(t),S); 12.END FOR 13.DetermineB(t+1)byf(Zi(t))inP2(t)∪{B(t)}; 14.P(t+1)←SEO(P2(t)); 15.t←t+1; 16.END WHILE 17.RETURN(B(t),f(B(t))); 与文献[4]中的FirEGA算法比较,CEGA算法在CRO算子和MUO算子过程中引入Core算法,交叉变异的算子只在核内进行,达到提升交叉变异效率。同时,易得CEGA的时间复杂度是O(n3)。 沿用文献[4]中所提出的四类D{0-1}KP实例数据,每类数据均包含规模依次等量递增的数据10种,关于数据的具体阐述可参考文献[4]。本文所提出新算法CEGA与文献[4]中FirEGA算法框架基本一致,且相应计算过程并无变化,因而相关参数与文献[4]设定一致:pc=0.8,pm=0.01,种群规模为50。 本文使用计算器为联想Y470型笔记本,CPU配置为Intel(R) Core(TM) i3-2350M CPU@2.3GHz。采用MATLAB 7.0进行问题进行建模求解,并将结果绘制成图,利用SPSS 21.0对所得结果进行检验。 CEGA算法对D{0-1}KP四类实例求解的结果见表1—表4。其中Opt为通过动态规划法(记为DPDKP)求解得到的实际最优解值,也即问题的理想最优解。Best、Worst和Mean分别为FirEGA和CEGA两类算法在30次独立计算中所得最优解、最差解、及结果的数学期望。Time1、Time2则分别表示FirEGA和CEGA两类算法在30次独立计算中算法收敛的平均迭代次数(单位:次)。为体现两种算法在求解精度方面的差异,这里通过计算近似比差异率来作为分析数据结果主要参数。其中,Best/Opt-1、Mean/Opt-1、Worst/Opt-1为最优解近似差异率、期望值近似差率和最差解近似差异率。 由表1—表4中的数据可知:CEGA求解UDKP实例的最优值近似比差异率在0.97%至2.07%范围内,平均值和最差值的近似比差异率在1.31%至3.01%范围内,而FirEGA求解结果对应的差异率范围为7.04%~12.61%、8.09%~13.58%。表明CEGA与FirEGA在求解UDKP实例中的结果差异明显,CEGA得到问题解得质量有显著性提升。CEGA算法求解WDKP实例对应的近似比差异率除WDKP10稍微差一点之外,其他9种实例计算结果均好于FirEGA。CEGA算法求解SDKP实例的最优值近似比差异率在0.47%至1.33%范围内,平均值和最差值的近似比差异率在0.68%至1.61%范围内,均优于FirEGA求解结果。CEGA算法求解IDKP实例的最优值近似比差异率在0.00%至0.15%范围内,平均值和最差值的近似比差异率在0.04%至0.78%范围内,与FirEGA算法相比,解得质量得到较大改善。 为更好的体现CEGA算法和FirEGA算法求解四类实例的效果,通过图1—图8分别给出它们两种算法求解四类实例的1-Best/Opt和Mean/Opt-1曲线对比图。 运用核算法,能够加速算法的收敛,而FirEGA算法容易存在收敛缓慢的问题,因而在FirEGA基础上改进得到的CEGA算法在收敛速度上,应优于FirEGA。由表1—表4可知,CEGA算法收敛速度明显优于FirEGA算法。为更加直观展示各算法收敛速度,将各自收敛代数数据Time1和Time2生成图9—图12。从图中不难发现,在收敛速度上CEGA算法比FirEGA有明显的提升。 表1 FirEGA和CEGA求解D{0-1}KP实例UDKP1-10的结果比较 表2 FirEGA和CEGA求解D{0-1}KP实例WDKP1-10的结果比较 表3 FirEGA和CEGA求解D{0-1}KP实例SDKP1-10的结果比较 表4 FirEGA和CEGA求解D{0-1}KP实例IDKP1-10的结果比较 为改善FirEGA算法求解D{0-1}KP问题易陷于局部最优解、收敛缓慢的问题,将核加速算法与遗传算法进行融合得到求解D{0-1}KP问题的核加速遗传算法CEGA。为验证算法的有效性,将CEGA用于求解文献[4]中给出的四类D{0-1}KP实例,由计算结果可知,无论是在解的质量还是收敛速度上,CEGA均优于FirEGA,表明CEGA算法在求解D{0-1}KP问题上是有效、可行的。 参考文献: [1] GUDER.Discounted Knapsack Problems for pairs of items[D].Nuremberg:University of Erlangen-Nurnberg,2005. [2] GULDAN B.Heuristic and exact algorithms for discounted knapsack prob1ems[D].Nuremberg: University of Erlangen-Nuremberg,2007. [3] RONG A Y.FIGUEIRA J R.KLAMROTH K.Dynamic programming based algorithms for the discounted {0-1} knapsack problem[J].Applied Mathematics and Computation.2012,218(12):6921-6933. [4] 贺毅朝,王熙照,李文斌,等.基于遗传算法求解折扣{0-1}背包问题的研究[J].计算机学报,2016,39(12):2614-2630. [5] HE Y C,WANG X Z,HE Y L,et al.Exact and approximate algorithms for discounted {0-1} knapsack problem[J].Information Sciences,2016,369(10):634-647. [6] GOLDBERG D E.Genetic Algorithms in Search,Optimization and Machine Learning[M].Boston:Addison-Welsley,1989. [7] JONG K A D.Analysis of the behavior of a class of genetic adaptive systems[D].Ann Arbor:Wiuersity of Michigan,1975. [8] 陈国良,王熙法,庄镇泉,等.遗传算法及其应用[M].北京:人民邮电出版社,2003. [9] RUDOLPH G,JONG K D.Convergence analysis of canonical genetic algorithms[J].IEEE Transactions on Neural Networks,1994,5(1):96-101. [10] JONG K D,Learning with genetic algorithms:An overview[J].Machine Learning,1988,3(3):121-138. [11] 周 明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999. [12] SCHMITT I M.Theory of genetic algorithms[J].Theoretical Computer Science,2001,259(1/2):1-61. [13] BALAS E,ZEMEL E.An Algorithm for Large Zero-One Knapsack Problems[J].Operations Research,1980,28(5):1130-1154. [14] PISINGER D.Core problems in Knapsack Algorithms[J].Operations Research,1999,47(4):570-575. [15] PISINGER D.An expanding-core algorithm for the exact 0-1 knapsack problem[J].European Journal of Operational Research,1995,87(1):175-187.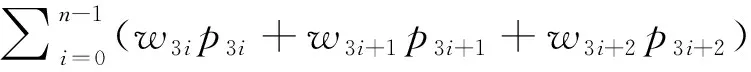
2 核算法
3 核加速遗传算法
4 实例计算与比较
4.1 计算结果
4.2 计算收敛速度比较


5 结语