无刷直流电机模糊PID控制系统研究

朱 霖

（马鞍山钢铁股份有限公司，安徽马鞍山，243000）

引言

无刷直流电机（以下简称BLDCM)相较传统有刷电机及交流电机具有更好的安全性和工作特性，如调速性能优良，动态响应迅速，速度/扭矩性能好以及使用寿命长等。目前，无刷电机已广泛应用于汽车、家用、计算机、工业自动化、医疗、航空航天等行业领域[1,2]。传统PID控制器因算法结构简单、不依赖模型控制、快速响应、稳定度高以及良好的可靠性等特点被广泛使用于速度控制系统[3]。BLDCM是一个具有非线性、强耦合及多变量的结构模型，使得一般常规PID控制方法无法实现预期的调控成效[4,5]。模糊PID控制综合了经典PID控制和模糊算法的功能特点，充分发挥了其综合的优势，对复杂且没有精确数学模型的系统表现出较好的控制性能。在电机的电流滞环控制模块中，转速调节过程包含电流限幅模块，因此常出现一定的积分饱和现象，造成超调量上升。模糊PID控制方法虽然可以从一定程度上降低超调量但不能消除[6]。本文针对解决积分饱和现象提出了一种抗饱和模糊PID控制算法，同时，设计并实现了一种基于STM32的地铁屏蔽门控制系统，并使该系统既保持较强的鲁棒性，又不存在超调。

1 无刷直流电机数学模型

由电机结构可知各相绕组在空间上互呈120°。各相反电动势为梯形波。以两相导通星型连接的三相六状态作为研究对象建立数学模型，需做如下假设[7]：

(1)电机参数相同且保持恒定，其气隙磁感应强度在空间呈梯形状；

(2)忽略定子铁心齿槽效应和空间谐波；

(3)定子与转子两者之间气隙均匀，不计磁路饱和；

(4)不计涡流和磁滞损耗；

(5)转子上没有阻尼绕组；

(6)不考虑电枢反应。

依据以上假设，电机的电压平衡方程为：

在式(1)中，R表示各种定子绕组的电阻，并且有Ra=Rb=Rc=Rs。L 表示各种定子绕组的自感，Lab、Lac、Lbc分别表示AB相、AC相、BC相两相之间绕组的互感。ua、ub、uc分别表示各定子电压。ia、ib、ic分别表示各定子电流。ea、eb、ec表示各反电动势。P是微分算子表达式，即P=d/dt。因为转子是永磁的，所以可以忽略转子的影响，因此有La=Lb=Lc=L，Lab=Lac=Lba=Lac=Lca=Lcb=M（M为定子绕组间互感）。在前述假设条件下，它们与转子位置没有关系，因此可以视做常数，这样上面的方程可改写为：

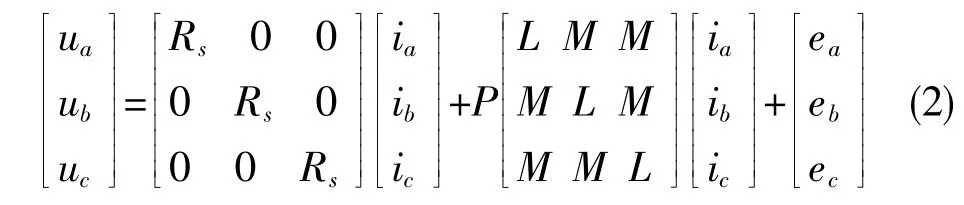
因电机绕组连接结构是三相星形且连接无中线，由基尔霍夫定律可知ia+ib+ic=0，则Mia+Mib+Mic=0；将上述两等式带入式(2)后，电压方程变成为如下形式：

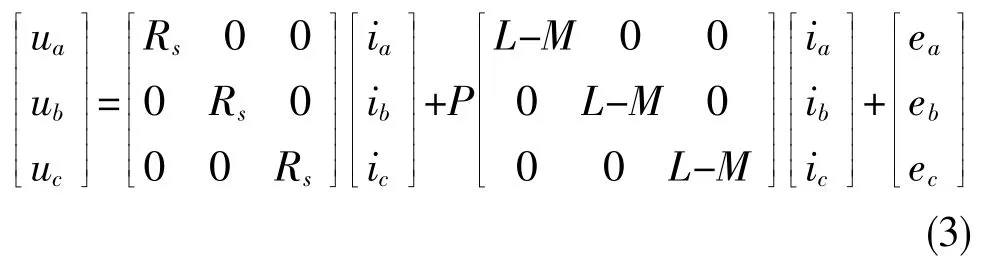
电磁转矩方程和机械运动方程为:

式中，ωn-电机的机械角速度；TL-负载转矩；B-阻尼系数；J-为转动惯量[8]。

2 系统结构

依据BLDCM的数学模型及工作原理，通过MATLAB/Simulink软件环境构建实验模型。本系统采用经典的转速-电流双闭环控制。其中电流环作为内环，转速环作为外环。选用电流滞环控制方法作为电流内环的调整方式，转速环选用抗饱和模糊PID控制。

系统结构如图1所示[9]。基于模块化的设计思想，图1所示的系统结构可以分为以下几个具有独立功能的子模块：速度控制器、电流控制器、换向逻辑、逆变器、电流检测单元、速度检测部分、位置信号、电机本体模型。系统仿真模型如图2所示。

图1 无刷直流电机系统结构

图2 BLDCM仿真模型

3 无刷直流电机速度控制

3.1 PID控制器

传统PID控制原理框图如图3所示。

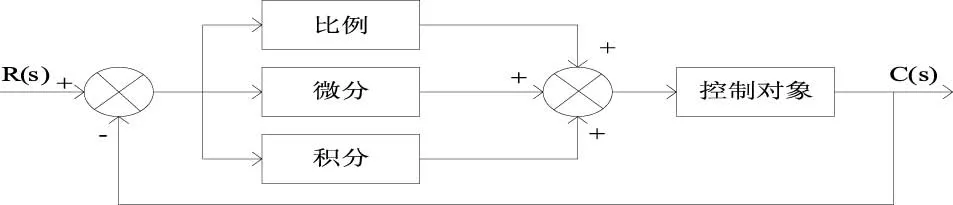
图3 PID控制器框图

传统PID传递函数为:

式（6）中，Kp代表比例系数；Ki代表积分控制参数；Kd代表微分系数。

PID控制器各调节环节的作用如下：

比例环节：对系统偏差成比例调节。可作为一个比例增益放大器，减少误差。比例调节作用有助于改善系统的动态性，但同时又损失其稳定性。

积分环节：一旦偏差出现，积分立即起调节作用，直到无静差存在，积分不在发挥作用。积分调节使系统稳定性上升。积分调节不能独立作为一个调控环节，常常同比例或者微分环节一起组成PI或PID控制。

微分环节：微分反映系统偏差的变化率。通过调整微起到超前矫正偏差的作用。因此，可以改善系统的动态性能。

3.2 模糊PID控制器

在电机双闭环调控过程中，转速外环起到主调节作用，电流内环调整电机力矩输出，抑制转速波动，增强了系统的抗干扰性。传统PID控制方法无法依据系统参量的变化规律做出合理的修正，鲁棒性差[10-13]。模糊PID能够实时修改PID参数，完成该参数的自整定过程，保证系统有较强的抗干扰性。控制结构图如图4所示[14]。

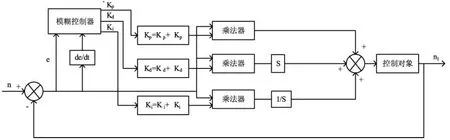
图4 模糊PID控制框图

如图4所示系统输入偏差为e、偏差变化率为de/dt。输出为 PID 的 3 个修正量 ΔKp，ΔKi，ΔKd。PID参数由以下公式得到[15]：

式中 K′p，K′i，K′d表示 PID 各控制参数初始设定值。ΔKp，ΔKi，ΔKd是通过模糊运算得出的调整增量。

当电机运行过程时，依据当前速度的偏差和及其偏差的变化增量，将其量化到对应论域，再依据控制规则表中各参数相对应的调整修正量，通过这样的策略达到3个控制参数在线调整的目的。

3.3 抗饱和模糊PID控制器

在电机电流滞环控制模块中，转速调节因电流限幅作用易造成积分饱和，使其输出超调量变大，模糊PID控制方法能一定程度使超调量减少，但始终无法完全消除。利用积分分离方法消除了超调量，同时又发挥了积分的调节作用。本设计把该方法与模糊PID控制算法进行有效整合，设计了一种抗饱和模糊PID控制方案。其控制器结构图如图5所示。

本文研究的主要内容是设计并完成一个抗积分饱和的二维模糊控制器。首先把该控制器的输入量设置为速度增量与速度变化量的增量，其次在经模糊运算之后，在线调整3个PID参数值。FIS推理控制器的类型为Mamdani。解模糊为重心法。

根据模糊设计规则首先对输入、输出量建立模糊集，然后设定论域，最后确定相应的隶属度函数:

图5 抗饱和模糊PID控制框图

1）输入与输出模糊子集使用7个划分等级。即e={负大（NB）、负中（NM）、负小（NS）、零（ZO）、正小（PS）、正中（PM）、正大（PB）}。

2）输入输出论域均为[-3,3]。

3）确定隶属度函数。选用输入、输出隶属度函数都为三角形曲线。

如表 1～3 所示为 ΔKp，ΔKi，ΔKd三个控制修正量的控制规则表，其中NB（Negative Big）为负大、NM（Negative Medium）为负中、NS（Negative Small）为负小、ZE（Zero）为零、PS（Positive Small）为正小、PM（Positive Medium）为正中，PB（Positive Big）为正大，它们用来表示隶属度关系。

表1 驻Kp的模糊规则

表3 驻Kd的模糊规则

在Simulink软件环境下，构建其控制器的模型如图6所示。

4 仿真与实验结果分析

选用电机参数为：定子绕组电阻为R=1 Ω，各绕组的自感与互感的差值(L-M)=0.0795 H，反电动势系数Ke=0.4，极对数P=1，转动惯量J=0.0008 kg·m2，阻尼系数 B=0.0002 N·m·s/rad，220 V 直流电压供电。

负载TL=1 N·m，给定速度n=100 r/min，在0.25 s负载从1 N·m增加到1.6 N·m。系统在传统PID，模糊PID，抗饱和模糊PID控制三种控制模式下的速度响应曲线如图7所示。从图7可以看出，模糊算法调节时间较短，超调量减小，系统鲁棒性增强，缺点是不能消除超调。抗饱和模糊PID控制到达稳态所耗时间更短，最重要的是系统不存在超调，系统鲁棒性较强。图8和图9给出抗饱和模糊PID控制的反电动势波形、相电流波形以及电磁转矩的波形。

本文选用STM32F103ZET6作为控制芯片，给定转速n=100 rad/s。在关门控制过程中，将当前电机转速通过串口发送至虚拟示波器软件。图10为转速和电流曲线截图。图10中纵坐标为放大100倍后的数值，横坐标为放大500倍后的数值，实际速度能够准确的跟随目标速度，系统保持较高的控制精度。

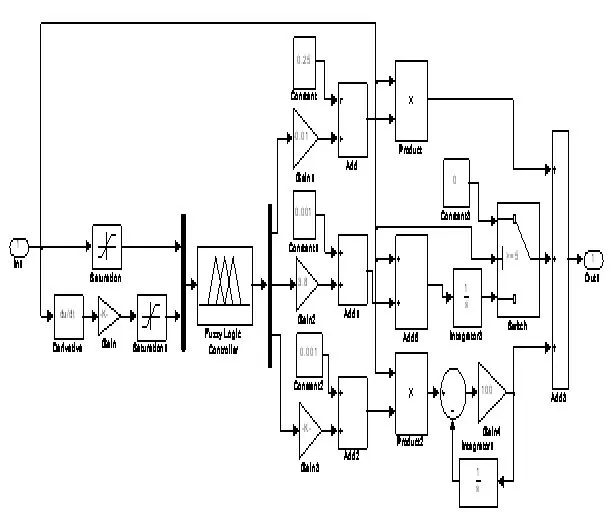
图6 抗饱和模糊PID控制器仿真模型

图7 传统PID、模糊PID和抗饱和模糊PID速度响应

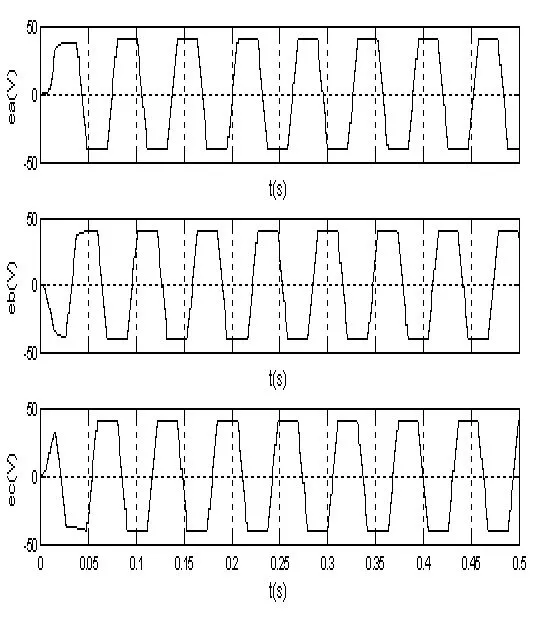
图8 抗饱和模糊PID控制的反电动势

图9 抗饱和模糊PID控制的相电流

图10 关门动作过程中电机转速和电流曲线

5 总结

本设计算法实现了将模糊PID控制与抗饱和处理方法结合起来，通过把该算法运用于BLDCM电流滞环控制系统并完成实验仿真。从实验结果可以得出：通过改进算法可实现完全消除积分饱和现象，降低速度超调量在1%以内，同时增强了系统的抗击扰动的能力，大大降低了系统的调整时间。

[1]易海涛,蒋猛,卢营蓬,寇杰,杜俊良.无位置传感器无刷直流电机驱动控制系统设计[J].西南师范大学学报（自然科学版）,2014,9(39):133-137.

[2]袁先圣,刘星,叶波.STM32的无刷直流电机控制系统设计[J].单片机与嵌入式系统应用,2013,10:17-20.

[3]Wei Yanyu,XuYongxiang,ZouJibin,et al.Current Limit Strategy for BLDC Motor Drive With Minimized DC-Link Capacitor[J].IEEE Transactions on Industrial Applications,2015,51(5):3907-3913.

[4]Cui Chenjun,Liu Gang,Wang Kun.A Novel Drive Method for High-Speed Brushless DC Motor Operating in a Wide Range[J].IEEE Transactions on Power Electronics,2015,30(9):4998-5008.

[5]Han Bangcheng,ZhengShiqiang.Design,Modeling,Fabrication,Back-to-Back Test of a Magnetic Bearing System for High-Speed BLDCM Application[J].J.Eng.Gas Turbines Power 2015,62(12):1-9.

[6]张勇,程小华.无刷直流电机抗饱和变结构PI控制研究[J].电气自动化,2014,36(4):7-9.

[7]潘晓磊,赵川,吕海立.无刷直流电机模糊自适应PID控制的研究[J].机电工程技术,2016,45（3）：85-89.

[8]GuDeying,Zhang Jinquan.Speed control of BLDCM Based on Compensated Fuzzy Neural Network[C].The 26th Chinese Control and Decision Conference, Changsha,China,2014:4541-4544.

[9]Xia Changliang,Li Xinmin.Z-Source Inverter-Based Approach to the Zero-Crossing Point Detection of Back EMF for Sensorless Brushless DC Motor[J].IEEE Transactions on Power Electronics,2014,30(3):1488-1498.

[10]刘慧博,王静,吴彦合.无刷直流电机模糊自适应PID控制研究与仿真[J].控制工程,2014,21(4):583-587.

[11]DuanHaibin,Gan Lu.Orthogonal Multiobjective Chemical Reaction Optimization Approach for the Brushless DC Motor Design[J].IEEE Transactions on Magnetics,2014,51(1):7000207.

[12]VashistBist,Bhim Singh.A PFC-Based BLDC Motor Drive Using a Canonical Switching Cell Converter[J].IEEE Transactions on Industrial Informatics,2014,10(2):1207-1215.

[13]XuYongxiang,Wei Yanyu,Wang Baochao,et al.A Novel Inverter Topology for Brushless DC Motor Drive to Shorten Commutation Time[J].IEEE Transactions on Industrial Electronics,2016,63(2):796-807.

[14]王云良,王继水,王敏其.无刷直流电机自适应模糊优化控制[J].电机与控制应用,2014,41(11):14-17.

[15]谢俊.基于DSP的无刷直流电机控制系统的设计与仿真研究[D].武汉理工大学,2010.