高精度射频功率测量系统设计及噪声分析

熊珀艺，孙向明，黄光明，王 东

（华中师范大学像素实验室 湖北 武汉 430079）

1 绪论

在现代通信系统中，随着射频技术的应用越来越广泛，对射频信号功率的测量精度要求也越来越高。传统的射频信号接收器采用混频技术，将射频信号与本地振荡器作混频，然后对混频后的信号进行采样分析，由于本地振荡器带来幅度噪声很大，因此，传统的射频信号接收器对信号幅度的测量精度不高。近年来高速ADC芯片的产生，实现了对射频信号的直接采样，大大的提升了射频功率的测量精度。本文介绍了一种基于高速ADC芯片的吸收式功率测量系统，分析了系统噪声对测量精度的影响，估算出该功率测量系统的相对精度能够达到10-7ppm（百万分之一）。

2 测量系统简介

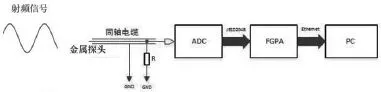
图1 高速ADC直接采样射频信号系统框图

本文提出的射频功率测量系统的结构如图1所示，该系统的测量噪声主要来源于ADC的量化噪声、热噪声以及采样时钟的相位噪声[1]。接下来给出系统噪声功率理论计算步骤，该过程运用了ADC12J4000芯片参数做参考。

3 系统噪声分析

3.1 热噪声

热噪声是由电子布朗运动引起的噪声，它存在于所有电子器件和传输介质中[2]。由于绝对零度无法达到，因此热噪声是不能够消除的。从图1可以看出，负载R的的热噪声会直接混入ADC的输入信号中，噪声功率Pt可表示为

其中KB为玻尔兹曼常数，单位为焦耳/开尔文，T为绝对温度，单位为开尔文，Δƒ为带宽，单位为赫兹。假设温度T为290K，热噪声的带宽Δƒ为2GHz，得出热噪声功率Pt为3.2×10-11W。

3.2 采样时钟的相位噪声

连续时间信号传入ADC后，我们需要对信号采样。理想情况下，采样间隔时间为常数，但实际上，时钟抖动会为采样结果带来相位噪声，假设被采样的信号为g(t)，相位噪声电压(RMS volts)2可以表示为[3]

其中σt是采样时钟的抖动，单位为(RMS seconds)。如果我们用一个简单的正弦信号来表示g(t)，例如

那么

如果正弦信号g(t)的频率为1.3GHz，信号幅度A为1V，时钟的抖动σt为100fs，可以算出σ2err为7.075×10-8V2，相位噪声功率为1.415×10-9W，负载为50Ω。

3.3 ADC的量化噪声

信号采样后会被ADC量化，此过程会给数据带来量化噪声。对于一个N位（ENOB）的ADC，量化器的最小分辨率Q为对于一个理想的量化过程，误差电压q(j)将在间均匀分布[4]，并且均匀覆盖所有的量化电平，因此量化噪声电压(RMS volts)2可表示为

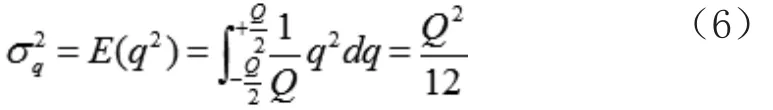
假设N为10，Vfs为2V，可以算出其量化噪声电压为3.179×10-7V2，量化噪声功率为6.358×10-8W，负载50Ω。

4 系统噪声对测量精度的影响

根据上述对系统噪声的分析与计算，我们可以估算出测量系统总噪声功率为6.5027×10-8W，从频域中看，该噪声均匀分布在每个频率点上，那么总噪声的功率谱密度可以表示为

其中Pnoise为总噪声功率，单位为瓦特；fs为采样时钟的频率，单位为赫兹。若被测信号频率为f0，采样时钟频率为fs，FFT数据长度为N，频率分辨率为fres，可以表示为

那么在频域内，频率点f0处，由系统噪声带来的功率测量结果的均方差（RMS watts）可以表示为

如果不考虑快速傅里叶变换对信号功率的估算误差，射频功率测量的相对精度与系统噪声的关系可以表示为

其中μP为功率测量结果的均值。假设N为1024，可以算出对μP为1mW的信号，测量的相对精度最高可达10-7。

为了验证上述三种噪声与信号功率测量精度的相关性，我们对一个已知信号叠加噪声并进行采样分析，其中被测信号为幅度1V，频率310Hz的正弦信号，采样时钟为10KHz，对采样数据作FFT变换，绘出的二维功率谱分布图如图2。由图可知312.5Hz处信号功率的估算相对精度为111.79ppm，这是由系统噪声与数据分析误差共同作用的结果。表1列出了FFT数据长度与结果的相对精度之间的关系，随着数据长度的提高，相对精度η慢慢变小，该结果与公式（13）基本吻合。

图2 二维功率谱分布图

表1 相对精度与傅里叶变换数据长度的关系

5 结语

根据上述理论推导及仿真，可得出利用采样率为4GHz、ENOB 10位的ADC直接测量毫瓦左右的射频信号功率，只考虑系统噪声的影响，测量的相对精度最高可达10-7。

[1]A.C.Ca'rdenas-Olaya,E.Rubiola,J.M.Friedt et al.Noise characterization of analog to digital converters for amplitude and phase noise measurements.Review of Scientific Instruments. 88:065108(2017).doi:10.1063/1.4984948

[2]J.B.Johnson.Thermal Agitation of Electricity in Conductors.Phys.Rev.32:97(1928).doi:10.1103/PhysRev.32.97

[3]P Smith.Little Known Characteristics of Phase Noise.Application Note AN-741,Analog Devices,Norwood, MA,USA,2004.

[4]H.B. Kushner, M.Meisner,A.V.Levy.Almost uniformity of quantization errors. IEEE Transactions on Instrumentation and Measurement.40(4):682-687(1991).doi:10.1109/19.85334