电磁调谐质量阻尼器的H2参数优化及对结构减震分析
罗一帆, 孙洪鑫, 王修勇
(湖南科技大学结构抗风与振动控制湖南省重点实验室, 湖南 湘潭 411201)
引 言
随着经济的发展,施工技术及设计理论的不断更新,建筑物的高度已经越来越高,刚度愈来愈小,自振周期在变长,在地震荷载或风荷载的作用下,容易引起建筑物的震/振动,影响建筑物的安全使用。大幅型振动可能破坏结构或二级组件,从而不适于人类居住。
为了抑制动力荷载下结构产生的响应,世界各国的学者们研究并开发了众多结构振动控制技术[1-4],根据所采取的控制措施是否需要外部能源可分为被动控制、主动控制、半主动控制和混合控制等。其中,被动控制是一种不需要外部能源的结构控制技术,从控制机理上可分为基础隔振和耗能吸能减振两大类。其中,耗能吸振减振主要包括耗能阻尼器和调谐阻尼器。在后者中,最简单实用的当属于调谐质量阻尼器(Tuned Mass Damper,TMD)。TMD的最早原型是动力吸振器[5],由一个质量块和一个弹簧构成,并未增加阻尼单元,当时主要用于控制不同类型的机械振动。近年来,随着TMD技术的应用越来越广泛,为了提高其性能,国内外的学者们分别对TMD减振理论的发展做出了卓越的贡献。
为了优化动力吸振器在外激励下的振动控制性能,Ormondroyd和 Den Hartog[6]在吸振器的原型上添加了黏弹性阻尼,提出了调谐吸振器的概念。同时Den Hartog[7]还在理论上通过固定点法推导了调谐吸振器在无主结构阻尼情况下的受简谐荷载作用的最优参数解析式。之后,Warburton[8]推导了主结构无阻尼时受简谐激励和白噪声激励作用下的TMD最优参数解析式。针对有主结构阻尼下的TMD的参数优化,也提出了众多优化理论和准则[9-12]。
另一方面,近年来国内外学者基于压电材料、电磁材料等材料,开展了能量收集与振动控制方面的设计、理论分析、仿真等工作。Nerves 和Scruggs 等[13]首次提出将土木结构振动能量收集,并用于结构振动控制的想法。国内学者孙作玉等[14- 15]利用“换能器”将结构的一部分振动能量以液压能的形式转换,并利用它作为主动控制的能源,提出了一种无能源主动控制方案。
基于TMD调谐耗能的特点,近年来利用TMD进行能量收集的理论也得以发展。Beherens等[16]最先提出了电磁换能器在隔震领域可用于实现振动控制与能量回收的想法。Inoue等[17]将电磁换能器与单自由度结构结合,并通过固定点法对系统的参数进行优化,得出理论解。Zuo等[18]通过实验验证了电磁换能器替代经典TMD中的黏性阻尼单元的可行性;Wen[19]对集能式调谐质量阻尼器与单自由度耦合结构在风振作用下的参数进行了优化。同时,李晓华[20]也提出了磁耦合调谐质量阻尼器的概念,并通过数值方法对系统进行参数优化。
本文基于经典TMD结构,将电磁换能器能量收集单元替代经典TMD系统中的阻尼器中的黏性阻尼单元,引入了电磁调谐质量阻尼器(Electromagnetic TMD,EMTMD)的概念,在对主结构进行减振的同时,对主结构的振动能量进行收集。同时本文还提出了EMTMD 关于H2的理论解析解。EMTMD的基本构造包括一个质量弹簧单元和基于电磁换能器的能量收集单元。与此同时,EMTMD阻尼值还可以通过电机的内阻与终端电阻值的大小来调节。通过电磁能量收集单元的能量收集,旨在为结构监测或振动控制的传感器提供一定的电能输入,从能量输出功率与作用力分析[21-23],收集的能量基本满足小型无线传感器(能耗几十mW)的供电问题,也为实现对于结构半主动振动控制系统供能提供了可能性。
本文基于EMTMD的原理,建立了能量收集单元、EMTMD和EMTMD对单自由度结构受地震作用时的动力学模型。然后基于H2优化理论,即主结构位移均方根值最优参数优化理论,进行参数优化,得到EMTMD的结构频率比、电磁阻尼比和机电耦合系数的最优解析解。通过频域和时域两种数值仿真方法,分析了EMTMD的减震及能量收集双重性能。
1 电磁调谐质量阻尼器(EMTMD)力学模型
1.1 EMTMD 工作原理
EMTMD的基本结构主要包括弹簧-质量单元,以及基于直线电机的能量收集单元,具体如图1所示。根据直线电机原理可以等效为一个电感L和一个内阻Ri;与此同时,直线电机与一交流直流转换器(AC/DC)、直流转换器(DC/DC)、能量储存单元相连,后三者的电阻可等效为外接电阻Re。直线电机与电路串联后,整个系统可以等效为一RL电路。
EMTMD的工作原理为:电磁换能器替换传统黏性阻尼器后,形成了电磁调谐质量阻尼器。当整个能量收集单元置于被控结构时,TMD质量块做直线运动,从而引起电磁发电机的动子相对于定子产生移动,随着动子的移动,线圈中的磁通量将发生改变,从而在线圈中产生感生电动势。在产生电动势时,等效为电磁力,形成振动能到电能的能量转化,从而进行对被控结构的振动控制。若在整个能量转化过程中,把能量收集储存,同时达到收集电能的效果。
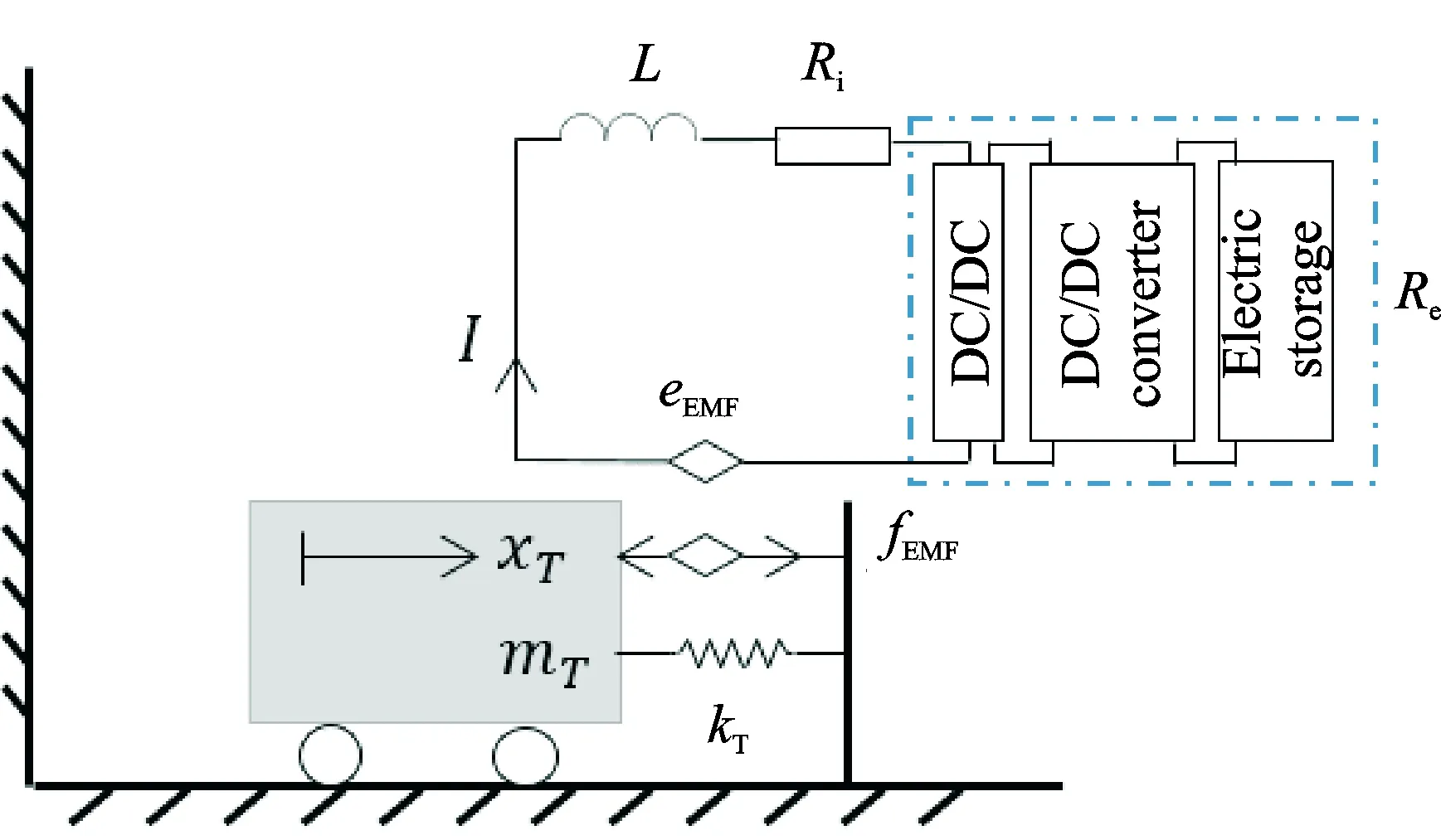
图1 EMTMD构造图Fig.1 The structural diagram of the EMTMD
1.2 能量收集单元力学模型
设在外部激励振幅作用下,根据基尔霍夫定律,不计电容,线圈回路电压平衡方程有
(1)
式中R表示线圈回路电阻且R=Ri+Re,Re是外接电阻,Ri是内阻;L是线圈回路电感;e是线圈移动时产生的感应电动势。
感应电动势的大小与磁场强度及相对移动速度成正比即
(2)
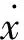
然后,回路中的电流会产生一反电动势力,反电动势力与回路中的电流成正比,力的方向总是与回路中的电流方向相反。则反电动势力为
(3)
式中kf是力常数。
在理想模型中
kf=ke
(4)
2 电磁调谐质量阻尼器(EMTMD)与单自由度结构耦合系统力学模型

图2 EMTMD耦合减震模型Fig.2 The coupling models of EMTMD
基于EMTMD的力学模型,依据达朗伯原理,耦合结构的力学模型建立如下
(5)
为了便于进行系统的参数优化,暂不考虑主结构的阻尼,通过拉普拉斯变换可得
(6)

(8)
令相对位移xr=xT-xs,上式可进一步化简
(9)

3 耦合系统减震模型的H2参数优化
3.1 耦合系统减震模型的传递函数
(10)
(11)
(12)
3.2 基于H2的参数优化

(13)
式中E[·]代表RMS值,〈·〉代表瞬时平均值,S0代表外激励的能量强度,单位是(m2·s)/rad。
则主结构位移xs的RMS值可以定义为
(14)
将式(14)带入式(13)中,评价指数PIv可以表示为
(15)
式(15)中的积分可以通过残数定理[25]求得,5阶积分简化后的公式见附录A。结合式(10),评价指标PIv可以表示为3个调谐参数结构频率比fT、机电耦合系数μk,电磁阻尼比ζe的函数形式
(16)
便于实现减震评价指标PIv最小化,即PIv对每个调谐参数的偏导数为零,则有
(17)
因此,通过式(16)和式(17),可有:
(18a)
(18b)
(18c)
通过求解方程(18),可得到
(19)
因此,相应的物理参数L,R,kT可以表示为
(20)
在地震荷载下的经典TMD的H2理论优化参数[26]表示为
(21)
4 频域数值分析
4.1 减震性能分析
4.1.1 最优状态下的H2调谐参数描述
由式(19)绘出3个调谐参数与质量比的关系图,如图3所示。从图中可以看出,随着EMTMD的质量比的增大,EMTMD的最优结构频率比会减小,且基本与质量比呈类似于线性关系,最优电磁阻尼比和机电耦合系数则会增大,不同的是最优电磁阻尼比的增速随着质量比的增大而变缓,机电耦合系数则基本上与质量比呈线性关系。
4.1.2 不同系统的减振性能对比
在质量比为0.02的情况下,主结构在无控状态、经典TMD控制状态和EMTMD控制状态下的主结构位移和相对位移频响对比如图4所示。从图中可以看出,在相同的质量比下,EMTMD的H2主结构位移减振性能要略优于经典TMD的性能。具体而言,EMTMD的主结构位移的传递函数Xn的峰值相对于经典TMD降低了4%。除此之外,当α的范围在0.7到1.3之间时,EMTMD的主结构位移的传递函数Xn的积分面积相对于经典TMD降低了0.9%。
4.1.3 不同质量比下EMTMD的减振性能对比
由图5可知,质量比越大,EMTMD的减振性能越好。

图3 最优H2调谐参数描述Fig.3 Graphical representations of the H2 tuning laws
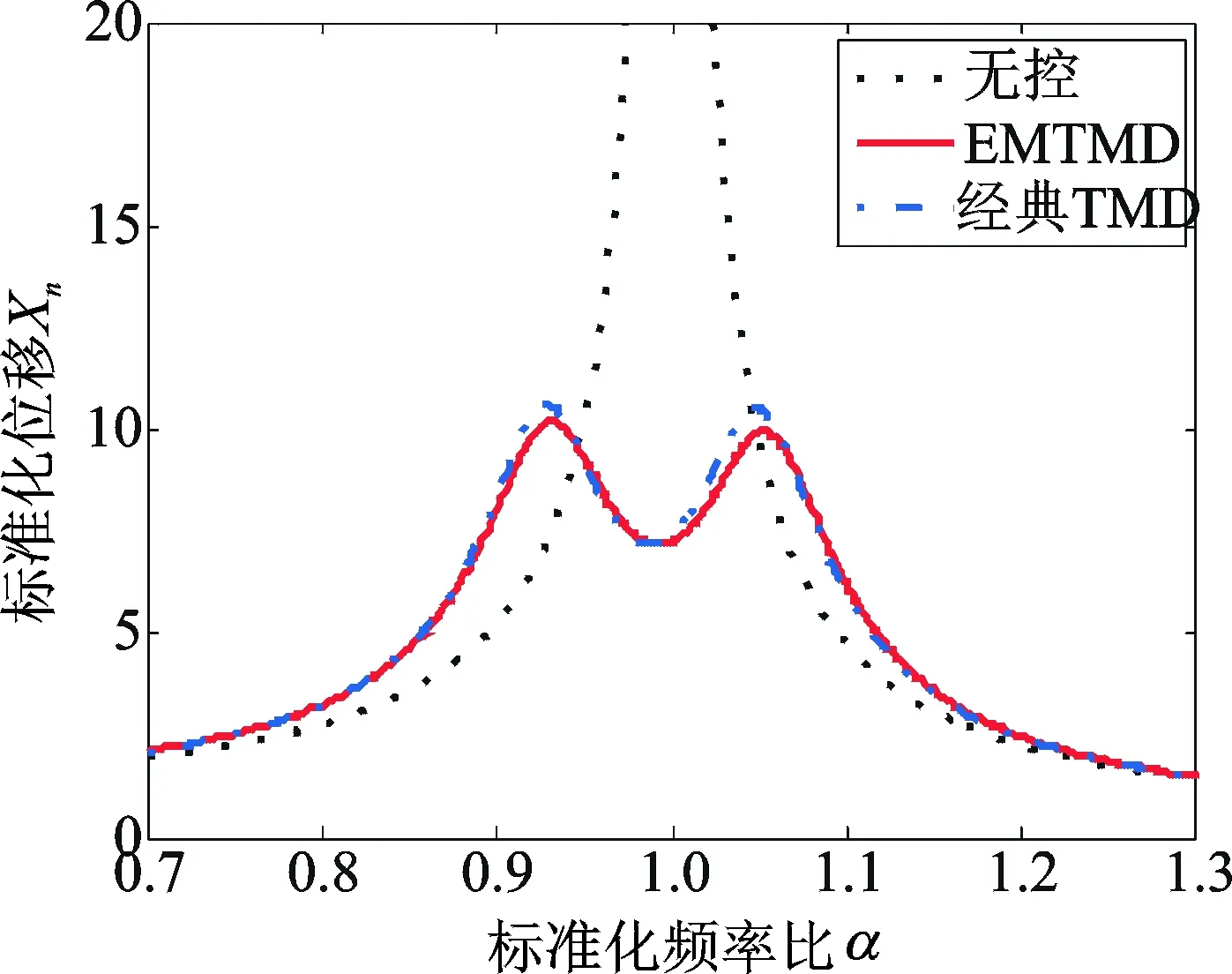
图4 质量比μ=0.02不同的TMD下的主结构位移频响
Fig.4 The frequencyresponses of the displacement of primary structure at the mass ratioμ of 0.02
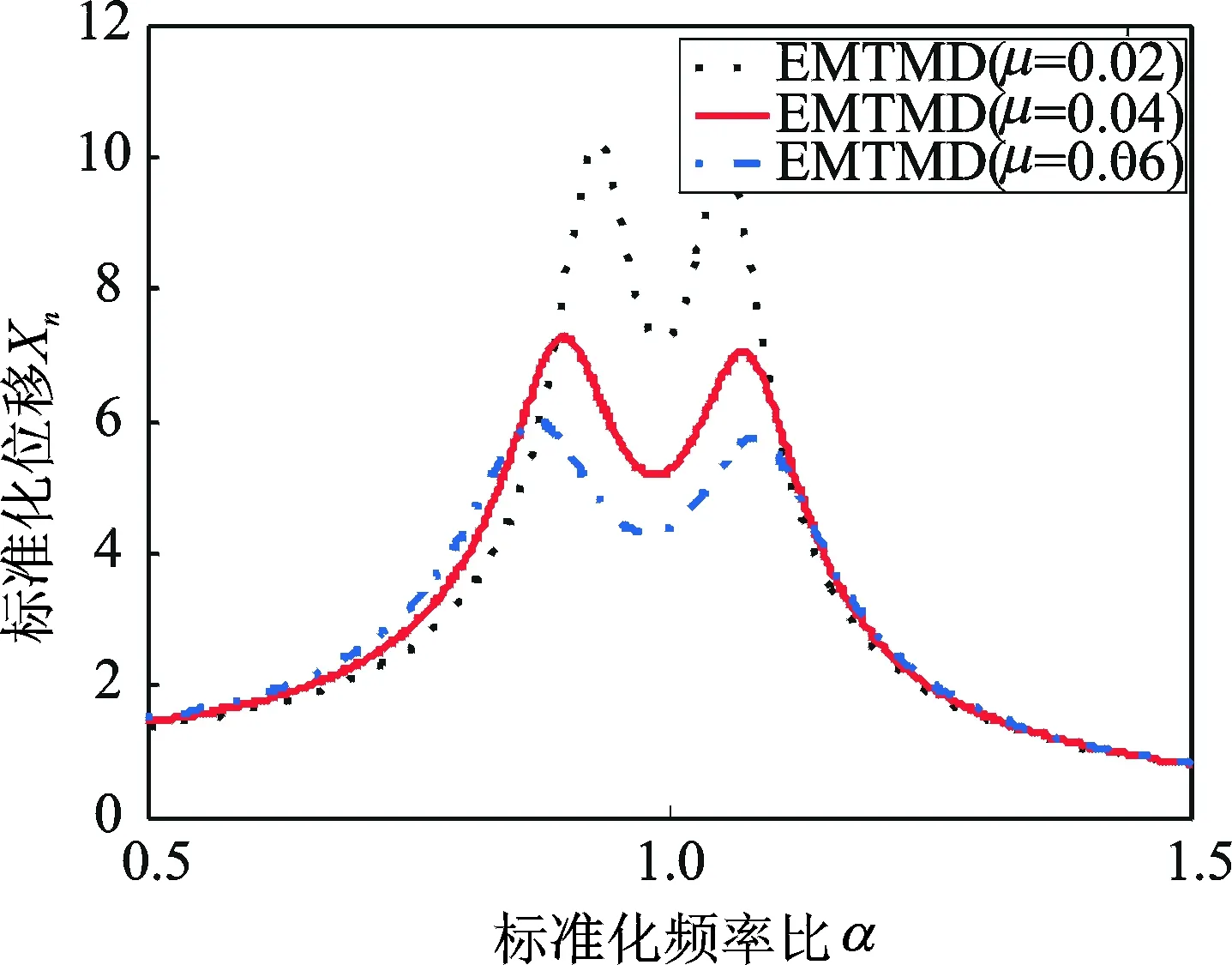
图5 在不同质量比下EMTMD的主结构位移频响
Fig.5 The frequency responses of the displacement of primary structure of EMTMD under different mass ratios
4.1.4 调谐参数的鲁棒性分析
在实际过程中,EMTMD很难调谐到最优状态,受到环境和时间的影响,一些参数可能会发生改变。减振性能随着相关参数的变化趋势如图6所示。从图中可以归纳出,EMTMD的主结构位移频响对结构频率比的变化比较敏感,而对电磁阻尼比和机电耦合系数则不是那么敏感。
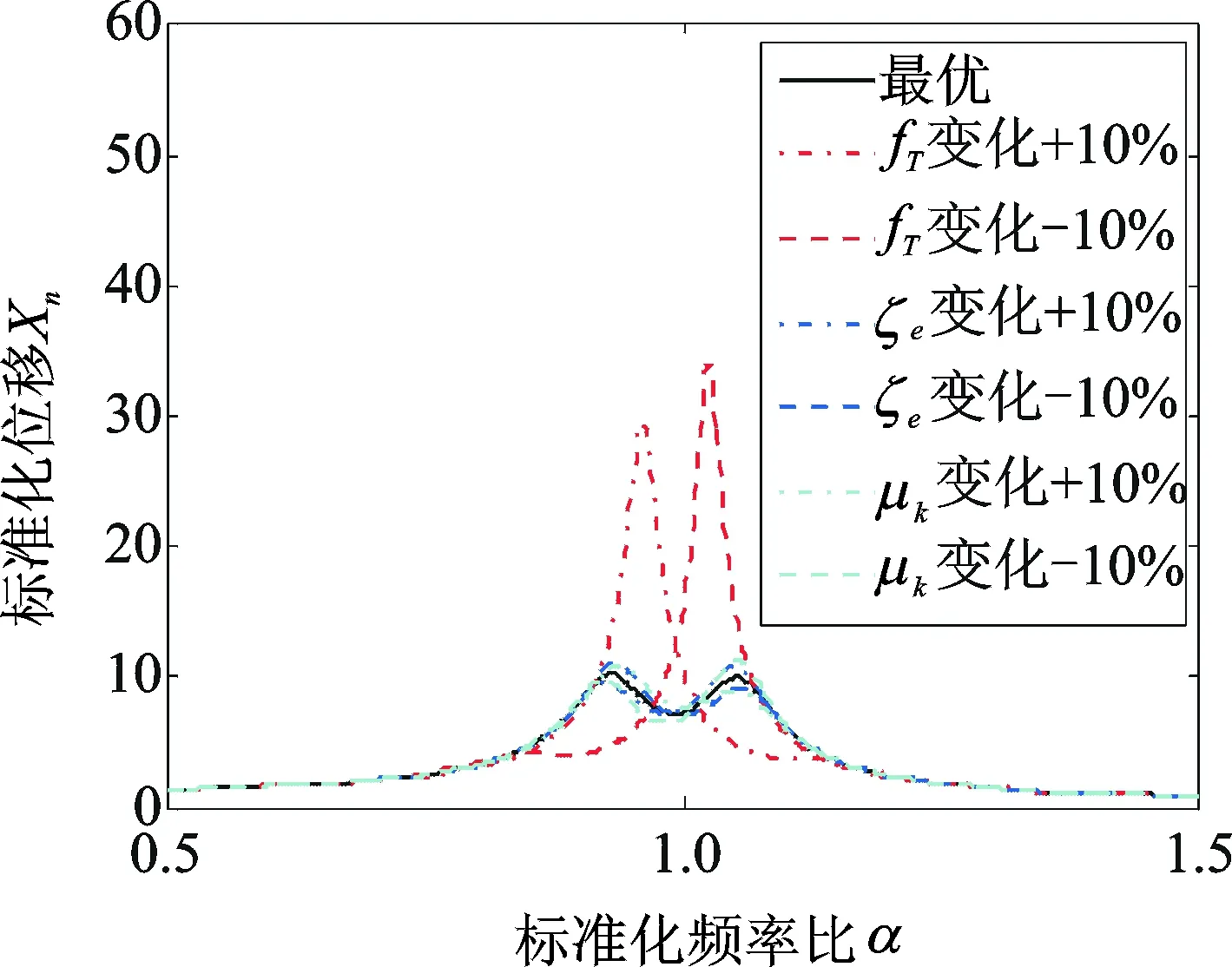
图6 EMTMD的调谐参数鲁棒性
Fig.6 The vibration performance change to the changes of the tuning parameters of EMTMD
4.2 能量收集分析
为了使EMTMD的能量回收效率最高,希望通过放大外接电阻Re的能量,作用在外接电阻Re的瞬时功率为
P(t)=ReI2
(22)
类似的,当系统在地震波加速度激励下,能量回收评价指标可以定义为
(23)
将式(12)带入式(23)中可得
(24)
5 时域数值分析
在本节中,通过4种地震波来时程分析EMTMD的减震和能量收集效果,相关分析如下:
5.1 理论模型
式(5)可以表述成另一种形式:
(25)
引入相对位移xr,上式可进一步化简
(26)
式(26)可以用矩阵形式表示为
(27)
其中
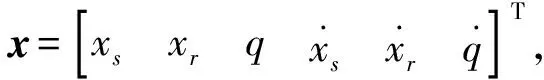
(28)

5.2 结构位移减震指标
(1)峰值减震评价指标
(29)
(30)
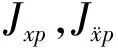
(2)均方差减震评价指标
(31)
(32)

5.3 仿真参数
为了进一步对本文提出的EMTMD两重功能进行仿真分析,仿真结果将会与最优状态下的经典TMD进行对比。此次仿真主结构参数选择的是10层框架结构,取其首阶模态参数,相关阻尼器参数根据H2最优解析解确定,具体如表1所示。
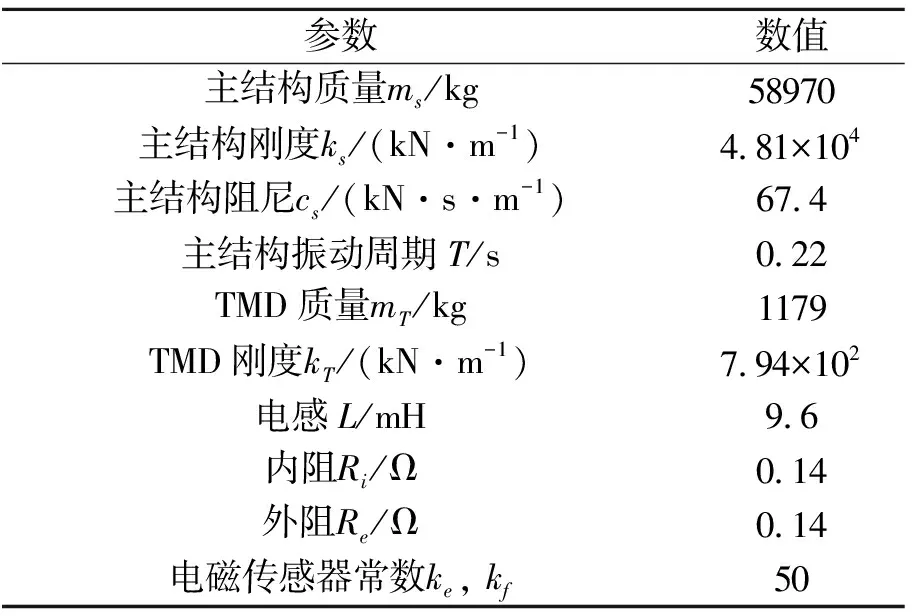
表1 仿真参数
5.4 减震仿真
本仿真过程中,选择典型的4种地震波进行仿真。为了便于对峰值减震进行分析,对地震加速度振幅调到200 cm/s2,4种地震波分别为:(1)ChiChi,(2)El Centro,(3)Kobe,(4)Northridge。地震波功率谱如图7所示,从图中可以知道每种地震波在不同周期的振幅强度。EMTMD的位移减震时程图如8所示,加速度减震时程图如9所示。相关位移和加速度峰值和均方值减震率如表2所示。

图7 地震波功率谱Fig.7 Response spectra for observed earthquake records
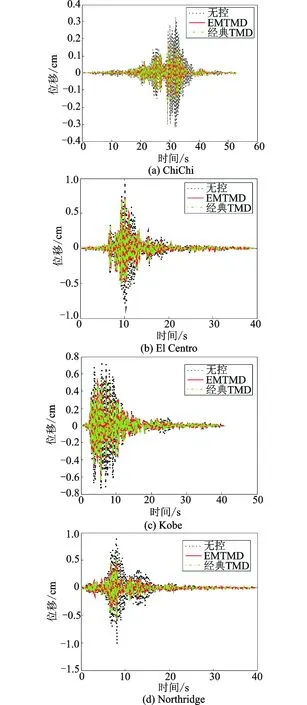
图8 位移减震时程图Fig.8 Time-history responses of displacements
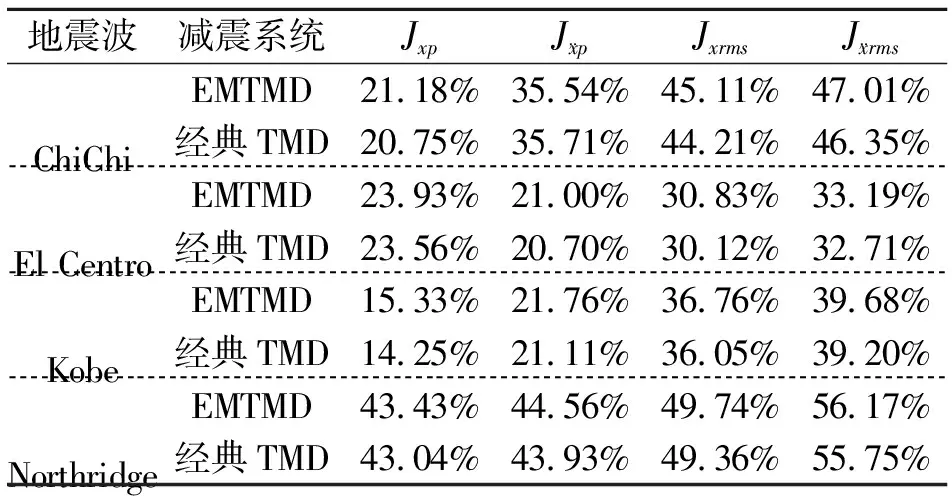
地震波减震系统JxpJx¨pJxrmsJx¨rmsChiChiEMTMD21.18%35.54%45.11%47.01%经典TMD20.75%35.71%44.21%46.35%El CentroEMTMD23.93%21.00%30.83%33.19%经典TMD23.56%20.70%30.12%32.71%KobeEMTMD15.33%21.76%36.76%39.68%经典TMD14.25%21.11%36.05%39.20%NorthridgeEMTMD43.43%44.56%49.74%56.17%经典TMD43.04%43.93%49.36%55.75%

图9 加速度减震时程图Fig.9 Time-history responses of accelerations
由表2可知,总体而言,相对于经典TMD,EMTMD对于主结构的位移和加速度的峰值和均方值减震性能均有了提高。
5.5 能量收集仿真
EMTMD的能量收集时程如图10所示,相关能量收集指标如表3所示。
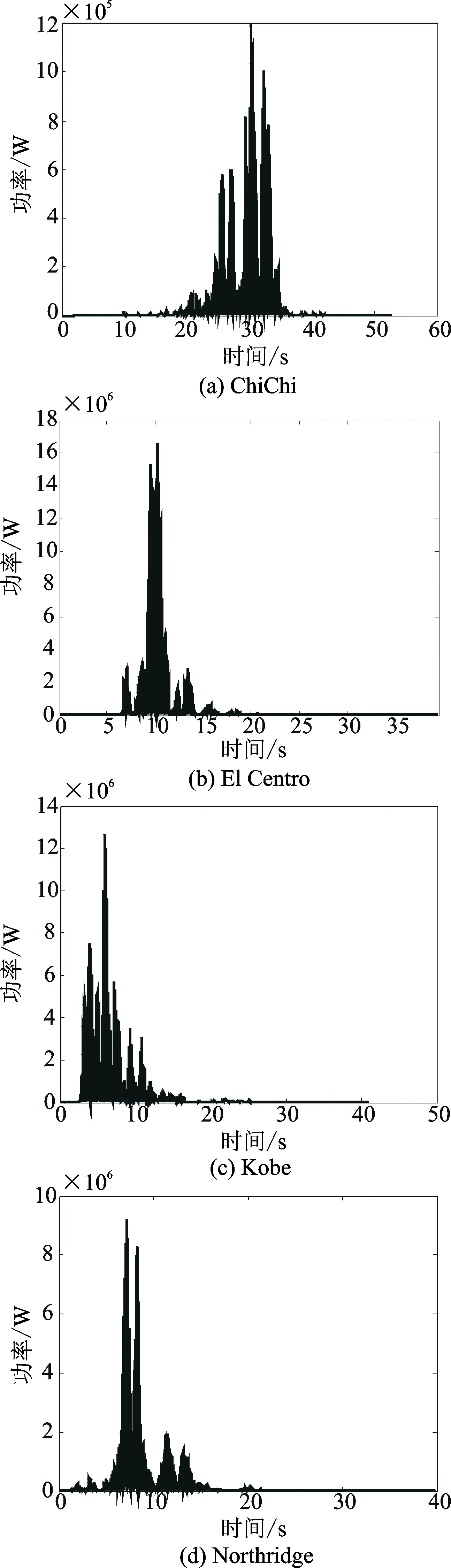
图10 能量收集功率时程图
Fig.10 Time histories of energy harvesting power
表3 能量指标
Tab.3 The indicators of the power

地震波峰值功率/W平均功率/W回收能量/J峰值电压/VChiChi1.19×1064.33×1042.29×1064.09×102El Centro1.66×1074.05×1051.60×1071.53×103Kobe1.26×1073.77×1051.54×1061.33×103Northridge9.25×1062.32×1059.27×1061.14×103
由图10和表3可知,EMTMD与经典TMD相比,其减振性能相当的情况,能够获得一定的能量收集效果。4种地震荷载仿真下,El Centro的收集能量最多,平均功率达4.05×105W,对应的峰值电压为1.53×103V。
6 结 论
本文基于经典TMD,引入电磁换能器代替黏性阻尼单元,形成具有结构减震与能量收集双重功能的新型电磁耦合调谐质量阻尼器。并且建立了能量收集单元、EMTMD、EMTMD与单自由度结构耦合减震模型的动力学模型。然后基于H2理论,即主结构位移均方根值最小优化理论,对耦合模型进行了参数优化,得到最优参数的理论解。利用所得参数数值仿真分析了耦合减震模型的减震和能量收集性能。具体结论如下:
(1)基于H2优化理论与残值定理,建立了主结构位移均方根最优的表达式,并获得了主结构的最优状况下的结构频率比、电磁阻尼比和机电耦合系数的解析表达式。
(2)频域分析可知,随着TMD质量比的增大,最优结构频率比会减小,而最优电磁阻尼比和机电耦合系数则会增大,EMTMD的减振性能则会越来越好。在相同的质量比下,EMTMD对于主结构位移频响减振效果略优于经典TMD的性能。
(3)时域数值分析的结果基本与频域分析基本相当,但是增加能量转化装置的EMTMD能够进行能量收集,如在EI Centro地震荷载时,收集的平均功率达4.05×105W,对应的峰值电压为1.53×103V。
[1] Yao J T P. Concept of structural control [J]. Journal of the Structural Division, 1972, 98(7): 1567—1574.
[2] Soong T T, Jr B F S. Supplemental energy dissipation: state-of-the-art and state-of-the-practice [J]. Engineering Structures, 2002, 24(3): 243—259.
[3] 茹继平. 土木基础设施减灾基础研究进展与趋势 [J]. 土木工程学报, 2000, 33(6): 1—5.
Ru Jiping. Development of fundamental researches on disaster mitigation of civil infrastructure systems [J]. China Civil Engineering Journal, 2000, 33(6): 1—5.
[4] 欧进萍. 结构振动控制:主动、半主动和智能控制 [M]. 北京:科学出版社, 2003.
[5] Frahm H. Device for Damping Vibrations of Bodies [M]. US. 1911.
[6] Ormondroyd J, Hartog J P D. The theory of dynamic vibration absorber [J]. Journal of Applied Mechanics, 1928, 49: A9—A22.
[7] Hartog, De J P. Mechanical Vibrations [M].4th ed . McGraw-Hill Book Company,Inc., 1956.
[8] Warburton G B. Optimum absorber parameters for various combinations of response and excitation parameters [J]. Earthquake Engineering & Structural Dynamics, 1982, 10(3): 381—401.
[9] Ghosh A, Basu B. A closed-form optimal tuning criterion for TMD in damped structures [J]. Structural Control & Health Monitoring, 2007, 14(4): 681—692.
[10] Anh N D, Nguyen N X. Design of TMD for damped linear structures using the dual criterion of equivalent linearization method [J]. International Journal of Mechanical Sciences, 2013, 77(77): 164—170.
[11] 李春祥, 熊学玉, 程 斌. 基于参数组合和加速度传递函数的最优MTMD研究 [J]. 振动与冲击, 2001, 20(3): 50—54.
Li Chunxiang, Xiong Xueyu, Cheng Bin. Research on the optimum MTMD based on parameter combinations and acceleration transfer function [J]. Journal of Vibration and Shock, 2001, 20(3): 50—54.
[12] 王 磊, 谭 平, 赵卿卿. 随机结构-TMD 优化设计与概率密度演化研究 [J]. 振动工程学报, 2015, 28(2): 285—290.
Wang Lei, Tan Ping, Zhao Qingqing. Optimal design and probability density evolution analysis of tuned mass damper for stochastic structures [J]. Journal of Vibration Eingineering, 2015, 28(2): 285—290.
[13] Nerves A C, Krishnan R. A strategy for active control of tall civil structures using regenerative electric actuators [C]. Proceedings of 11th ASCE Engineering Mechanics Specialists Conference, Florida, 1996, 503-506.
[14] 孙作玉, 刘 季. 结构振动的无能源主动控制 [J]. 地震工程与工程振动, 1999, 19(3): 102—105.
Sun Zuoyu, Liu Ji. Active structural vibration conrol without power supply[J], Earthquake Engineering and Eingineering Vibration, 1999, 19(3): 102—105.
[15] 张永山, 孙作玉, 何玉敖. 换能器与作动器同层布置时的无能源主动控制 [J]. 哈尔滨工业大学学报, 2001, 33(3): 333—335.
Zhang Yingshan, Sun Zuoyu, He Yuao. ACWPS with transducer and actuator placed on the same floor [J]. Journal of Harbin Institute of Technology, 2001, 33(3): 333—335.
[16] Behrens S, Fleming A J, Moheimani S O R. Vibration isolation using a shunted electromagnetic transducer [C]. Proc. Spie, Smart Structure and Materials, 2004, 5386:506—515.
[17] Inoue T, Ishida Y, Sumi M. Vibration suppression using electromagnetic resonant shunt damper [J]. Journal of Vibration & Acoustics, 2008, 130(4): 2727—2747.
[18] Tang X, Zuo L. Simulation and experiment validation of simultaneous vibration control and energy harvesting from buildings using Tuned Mass Dampers [C]. Proceedings of the American Control Conference, San Francisco: CA, 2012: 3134—3139.
[19] Cui W, Tang X, Zuo L. H2optimization of electricity-generating tuned mass dampers for simultaneous vibration control and energy harvesting [J]. Proceeding of SPIE—The International Society for Optical Engineering, 2013, 8688(3): 1—7.
[20] 李晓华, 王宝基, 薛中会. 磁耦合调谐质量阻尼器的参数优化及减振效果 [J]. 河南科技大学学报自然科学版, 2014 (4): 86—91.
Li Xiaohua, Wang Baoji, Xue Zhonghui. Parameter optimization and vibration control effect of TMD with magnetic coupling [J]. Journal of Henan University of Science and Technology: Natural Sciennce, 2014, (4): 86—91.
[21] 陈政清, 汪志昊. 基于能量回收的土木工程结构振动控制 [J]. 建筑科学与工程学报, 2009, 26(2): 9—14.
Chen Zhengqing, Wang Zhihao. Structural vibration Control based on the energy harvesting in civil engineering [J]. Journal of Architecture and Civil Engineering, 2009, 26(2): 9—14.
[22] Shen W, Zhu S. Harvesting energy via electromagnetic damper: Application to bridge stay cables [J]. Journal of Intelligent Material Systems and Structures, 2015, 26(1): 3—19.
[23] Zuo L, Cui W. Dual-functional energy-harvesting and vibration control: electromagnetic resonant shunt series tuned mass dampers [J]. Journal of Vibration and Acoustics, 2013, 135(5): 510181—510189.
[24] Doyle J. Robust and optimal control [J]. IEEE Conference on Decision and Control, 2002, 2(97): 1595—1598.
[25] Nishihara O, Asami T. Closed-form solutions to the exact optimizations of dynamic vibration absorbers (minimizations of the maximum amplitude magnification factors) [J]. Journal of Vibration & Acoustics, 2002, 124(4): 576—582.
[26] Asami T, Nishihara O, Baz A M. Analytical Solutions to H∞and H2optimization of dynamic vibration absorbers attached to damped linear systems [J]. Journal of Vibration & Acoustics, 2002, 124(2): 284—295.

