基于自适应学习的量子神经网络振动信号压缩
王怀光, 李 胜,吴定海, 王 强
(1.陆军工程大学石家庄校区七系, 河北 石家庄 050003; 2. 陆军装甲兵研究所, 北京 100072)
引 言
对装备进行状态监测与故障诊断是形成保障能力的关键因素。分布式在线监测系统能够实时监测装备完整运行状态,及时发现装备已发生或潜在的故障,给出维修保障信息[1]。现场状态信息的实时监控是复杂装备分布式监测系统实用性的根本保证[2]。长时间连续监测将产生大量数据信息,如果直接通过总线或无线网络发送,会造成网络拥堵,影响传输的连续性和可靠性。采取数据压缩方法减少传输数据量是提高状态监测实时性的有效方法。
基于振动的状态监测是最有效且常用的技术手段。振动信号一般为双精度浮点型,数据的重复率较低,采用霍夫曼[3]、LZW[4]和算术编码[5]等无损压缩方法,机械振动信号的压缩比较低,信号仍保留大量相关性和冗余性,不利于后续处理。
量子计算充分利用量子力学中量子态的纠缠性、相干叠加性和坍缩的特性,使得以量子计算为基础的量子算法具有并行计算、指数级存储和指数加速的作用,在计算复杂度、收敛性等方面,明显优于传统常规算法[6]。量子神经网络是一种基于量子计算的神经网络,是目前研究的热点,在故障诊断[7]、网络通信[8]、信号检测[9]等领域得到了应用。鉴于量子神经网络在信号处理中表现出的巨大优势,本文将神经网络应用于机械振动信号数据压缩,解决振动状态监测过程中大量振动信号的压缩问题。
量子神经网络模型采用梯度下降法进行优化,但在优化过程中,并没有充分考虑3个参数在调整时的相互影响,从而导致数值局部收敛,影响了振动信号处理后的数据压缩效率。为提高信号压缩比,加快运算速度,降低重构误差,提出了一种基于自适应学习的量子神经网络振动信号压缩方法。该方法采用量子编码方式,利用共轭梯度法对网络参数进行更新,自适应地选择学习速率,改善振动信号处理效果。实测信号应用表明,本文方法能够在增加振动信号压缩比的同时,降低了均方根误差,缩短算法运行时间,能够更好地满足数据传输的要求。
1 量子神经网络模型
量子神经网络基础结构为量子比特和量子门组成的量子神经元,量子神经元与普通神经元根据特定的连接规则,按照一定的拓扑结构进行组合,主要由输入层、多个隐含层和输出层等构成[10]。
根据实际需要,采用含有1个隐含层的3层量子神经网络对振动信号进行压缩。图1给出了3层量子神经网络模型的结构,输入层有n个量子神经元,隐含层有p个量子神经元,输出层有m个普通神经元。
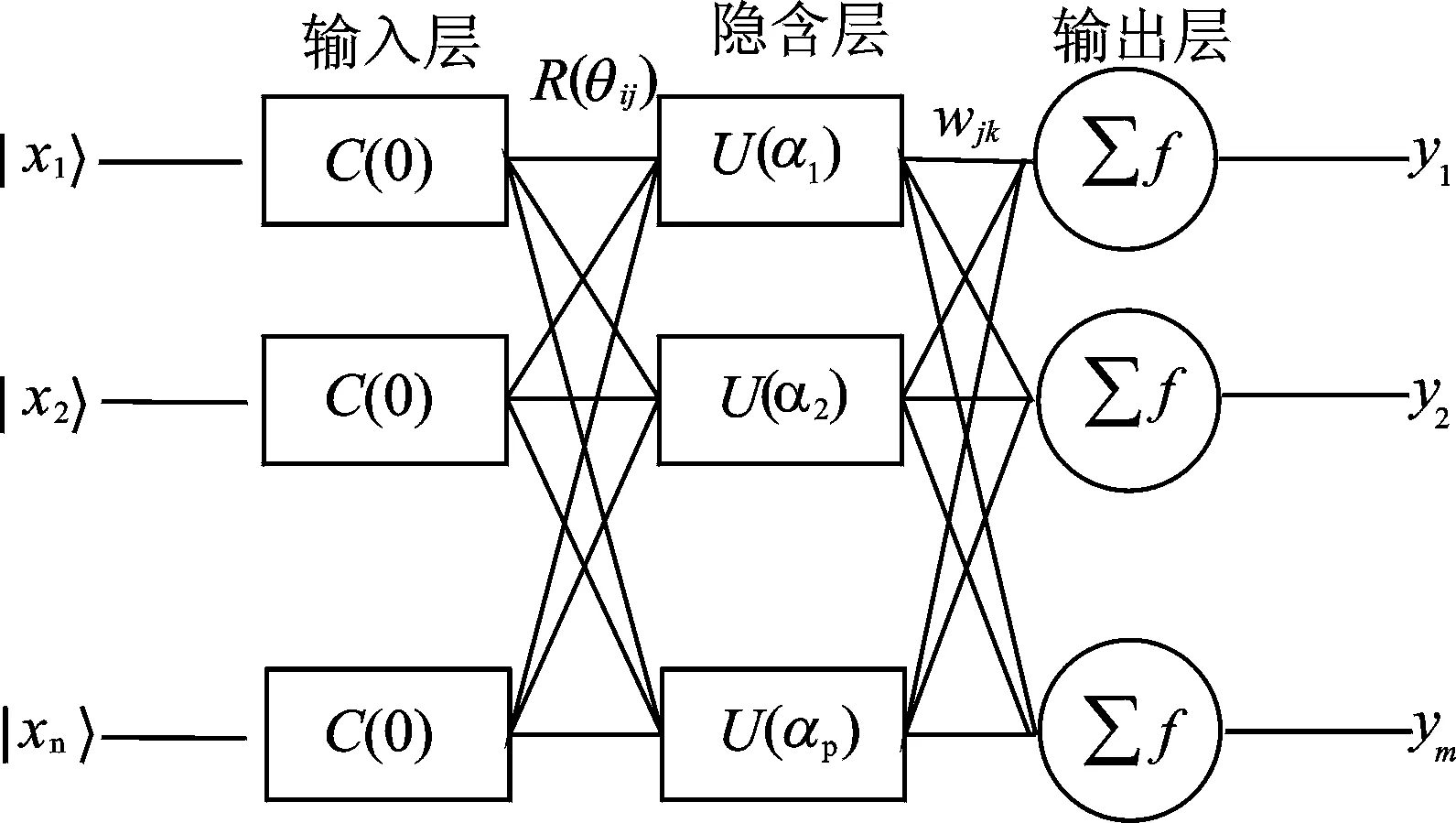
图1 量子神经网络的3层模型Fig.1 Quantum neural network model of three layers

U(αj)=C(g(αj))=
(1)
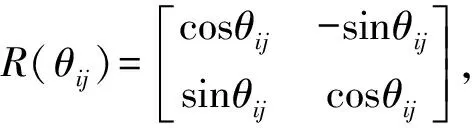
(2)
则
(3)

(4)
(5)
式中i=1,2,…,n;j=1,2,…,p;k=1,2,…,m。
1.1 量子编码
在量子神经网络中,量子态是输入的主要形式,因此,需要将实值样本转换为量子位,以便于进行编码。
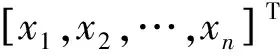
xi〉=cosφi0〉+sinφi1〉=
(6)
也可以表示为
(7)
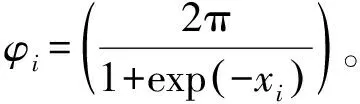
1.2 参数更新
在量子神经网络模型中,需要对3个参数进行更新,旋转角度θij、翻转权值αj和连接权值wjk。定义误差精度函数E为
(8)
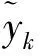

根据梯度下降法可得:
(9)
(10)
(11)
参数θij,αj和wjk的更新公式为:
θijt+1=θijt+ηΔθij
(12)
αjt+1=αjt+ηΔαj
(13)
wjkt+1=wjkt+ηΔwjk
(14)
式中t为训练次数,η为学习速率。
1.3 算法的步骤
(1)对输入数据进行量子编码;
(2)初始化网络参数:确定输入层神经元和隐含层神经元的数量;初始化旋转角度θij、翻转权值αj和连接权值wjk;确定训练次数t、学习速率η和误差精度E;
(3)按公式(4),(5)计算网络各层的输出,根据公式(9)~(14)修正网络中的参数;
(4)按公式(8)计算误差精度E,若达到误差精度或者训练次数,转到(5);否则转到(3),继续迭代计算;
(5)将隐含层输出作为信号的压缩结果;保存旋转角度θij、翻转权值αj和连接权值wjk。
2 基于量子神经网络的数据压缩方法
利用量子神经网络对一个含有n个点的振动信号进行压缩编码时,网络的输入层和输出层取相同的n个神经元,隐含层含有k个神经元,且k 图2 基于量子神经网络的压缩模型Fig.2 Compression model based on quantum neural network 在量子神经网络的压缩模型中,编码过程在输入层和隐含层之间,其权值矩阵为一个编码器;而解码过程在隐含层和输出层之间,其权值矩阵为一个解码器。 原始信号经过网络的训练后,在隐含层得到的输出结果就是原始信号的压缩编码,再通过输出层的权值矩阵解码出原始信号。隐含层的输出结果通过量化器经过合适的信道传送出去。 量子神经网络的压缩比(Signal Compression Ratio,SCR)[11]计算公式如下: (15) 因此,可以根据不同的压缩比来确定隐含层神经元的数量。输入层神经元数目就是原始信号的数量,隐含层神经元数目就是信号压缩后的数量。 由于量子神经网络采用了量子计算,而量子算法具有并行计算、指数级存储容量和算法加速等优点,因此,算法可以缩短运行时间,加快收敛速度。需要特别指出的是,量子神经网络基本实现了量子力学的基本思想,但要想实现真正的“量子计算”,需要建立量子计算的硬件设备[12]。 信号压缩比是根据不同的隐含层神经元数量决定的,根据不同的压缩比,即不同的隐含层神经元数量,来计算重构误差,因此,对信号来说,压缩比是变动的,需要找到合适的压缩比。将信号的均方根误差[13](Root Mean Square Error, RMSE)作为信号压缩评价指标 (16) 采用量子神经网络模型对信号进行压缩,随着隐含层神经元数量的减少,其压缩比增大,信号均方根误差也逐渐下降。但是,由于神经网络模型结构的特点,当数量下降到一定程度时,由于神经元数量不足以支撑其压缩,导致均方根误差又逐渐增大,因此,选择合适的隐含层神经元数量非常重要。 基于量子神经网络的数据压缩方法,模型中采用梯度下降法进行优化,并没有考虑3个参数在调整时的相互影响,从而会导致数值局部收敛。针对上述问题,论文提出了一种基于自适应学习的量子神经网络振动信号压缩方法(Quantum Neural Network Based on Self Adaptive Study,SAQNN)。在自适应学习量子神经网络中,采用共轭梯度法对3个参数θij,αj和wjk进行更新。共轭梯度法不仅克服了梯度下降法局部收敛的缺点,而且避免了矩阵存储和矩阵求逆的问题。 3个参数的梯度为: (17) (18) (19) 根据共轭梯度法可得 (20) pj+1θ=-θij+βjpj(θ) (21) (22) (23) pj+1α=-αj+βjpjα (24) (25) (26) pj+1w=-wij+βjpjw (27) (28) 式中j=0,1,2,…,n-1,A为Hessian矩阵。 因此,3个参数θij,αj和wjk的更新公式为: (29) (30) (31) 式中η为学习速率,t为训练次数。 自适应学习的基本原理就是根据误差精度的变化而自适应调整学习速率。在自适应学习量子神经网络中,根据公式(8)定义的误差精度函数,对学习速率进行调整。 振动信号误差精度的大小决定了信号的压缩质量,如信号的整体误差精度小,可以减缓学习速率,更精确的逼近;信号的整体误差精度大,可以加快学习速率,更加快速的逼近。因此,对学习速率自适应调整,既能保证信号整体质量,又能进一步提高压缩比。自适应学习量子神经网络压缩方法根据信号的相似性原则,将信号分为加速区、正常区和减缓区三个部分,根据误差精度函数,对公式(29),(30),(31)采用如下的自适应调整机制。 (1)计算一维振动信号的整体误差精度E(t); (2)当处于2Et≤Et+1(加速区)时,由于误差精度较大,需要加快学习速率,因此,使得ηt+1=1.5η0; (3)当处于Et≤Et+1<2Et(正常区)时,则ηt+1=η0; (4)当处于Et+1 式中η0为初始设定的学习速率。 为验证基于自适应学习的量子神经网络振动信号压缩方法,将其应用于自行火炮变速箱振动信号的数据压缩中,将QNN算法与SAQNN算法进行对比,算法参数的设置都相同。其参数设置为:误差精度为0.01,迭代步数为500,初始学习速率为0.9,翻转权值αj的初始值为α=0.25π,旋转角度θij和连接权值wjk初始值为rand=0,0.01π。 在变速箱振动实验台架上,采用CA-YD-185型振动传感器,对变速箱振动信号进行采集。采用YGM506型光电编码器拾取主轴旋转脉冲信号,光电编码器安装在发动机的输出轴上,变速箱振动实验台如图3所示。 图3 变速箱振动实验台Fig.3 The vibration test-bed of gear case 变速箱为二级传动齿轮箱,含有两对齿轮副,一对齿轮副齿数为25,50;另一对为18,91,采样频率为6400Hz,输入轴转速1491 r/min。在实验中,对变速箱3种工作状态下的振动信号进行采集,采集结果如图4所示。 实验共采集了50个信号,采用留一法训练网络。留一法是交叉验证的一种方法,即把每一个样本作为测试样本,其余N-1个样本作为训练样本,并以测试结果的平均值来衡量算法性能。图5给出了两种方法3种工作状态变速箱振动信号压缩比与均方根误差间的关系。 图4 齿轮在3种状态下的信号时域波形Fig.4 Time domain waveform of gears signal in three conditions 由图5可以看出,SAQNN方法比QNN的压缩比要高,并且在不同压缩比下都具有较小的均方根误差,说明SAQNN方法对振动信号的压缩能够获得更好的重构质量。 将变速箱3种工作状态下的振动信号输入到两种算法中,并列出了运行50次后的平均压缩结果,如表1所示。与QNN相比,SAQNN方法压缩后的数据量最少,压缩比更高,执行时间减少。随着采集振动信号数据量的不断增加,减少的数据量相当可观,SAQNN方法能够更好地保证信号传输的稳定性和可靠性。 表1 两种算法比较结果 图5 压缩比与均方根误差间的关系Fig.5 The relation between compression ratio and RMSE 本文研究了基于量子神经网络的装备在线状态监测网络数据压缩方法,以量子神经网络隐含层输出作为信号压缩结果,采用共轭梯度的量子神经网络参数更新方法,并根据信号误差精度大小自适应地选择学习速率,解决了量子神经网络收敛性差和学习速率慢的问题。装备变速箱振动信号应用结果表明,所提数据压缩方法在保证振动信号实时在线传输条件下,具有较好的信号重构质量,在装备在线状态监测领域具有较好的应用前景。 [1] 邓志超. 自行火炮故障智能诊断与预测系统设计[D]. 南京: 南京理工大学, 2007. Deng Zhichao. The design of fault diagnosis and fault forecast system for self-propelled gun[D]. Nanjing: Nanjing University of Science and Technology, 2007. [2] Liu Z, Wang Q. Real time compression algorithm by wireless sensor network signals data acquisition[C]. International Symposium on Test Automation and Instrumentation, 2006: 492—496. [3] David A Huffman. Method for the construction of minimum redundancy codes[C]. Proceedings of the Institute of Radio Engineers, 1952: 1098—1101. [4] Welch T. A technique for high performance data compression[J]. Computer, 1984, 17(6): 8—19. [5] Rissanen J. Generalized kraft inequality and arithmetic coding of strings[J]. IBM Journal of Research and Development, 1976, 20(3): 198—203. [6] 孙 健, 张雄伟, 孙新建. 一种新的量子神经网络训练算法[J]. 信号处理,2011, 27(9): 1306—1312. Sun Jian, Zhang Hongwei, Sun Xinjian. A new training algorithm for Quantum Neural Networks[J]. Signal Processing,2011, 27(9): 1306—1312. [7] 徐小力, 左云波, 吴国新. 量子神经网络在旋转机组状态趋势预测中的应用[J]. 机械强度, 2010, 32(4): 526—530. Xu Xiaoli, Zuo Yunbo, Wu Guoxin, et al. Fault trend prediction of rotating machines based on quantum neural netwoek [J]. Journal of Mechanical Strength, 2010, 32(4): 526-530. [8] 赵 阳, 孙学斌, 周 正. 一种改进的量子神经网络频谱感知算法[J]. 无线电通信技术, 2015, 41(2): 7—11. Zhao Yang, Suo Xuebin, Zhou Zheng. A spectrum sensing algorithm in cognitive radio based on improved quantum neural network[J]. Radio Communications Technology, 2015, 41(2): 7—11. [9] 杨倩倩. 量子神经网络的MIMO信号检测技术[J]. 电脑知识与技术, 2008, 1 (7): 1342—1345. Yang Qianqian. MIMO detection based on quantum neural network[J]. Computer Knowledge and Technology, 2008, 1 (7): 1342—1345. [10] 涂淑琴, 张义青, 王美华, 等. 一种量子神经网络模型及改进学习算法[J]. 现代计算机, 2010,(13): 3—6. Tu Shuqin, Zhang Yiqing, Wang Meihua, et al. A quantum neural network model and its improved learning algorithm[J]. Modern Computer, 2010,(13): 3—6. [11] Qin J C, Bai Z Y. Design of new format for mass data compression[J]. The Journal of China Universities of Posts and Telecommunications, 2011, 18(1): 121—128. [12] 吴家安. 数据压缩技术及应用[M]. 北京: 科学出版社, 2009. Wu Jiaan. Data Compression Technology and Application[M]. Beijing: Science Press, 2009. [13] 李盼池, 宋考平, 杨二龙. 基于受控旋转门的量子神经网络模型算法及应用[J]. 控制与决策, 2011, 26(6): 898—901. Li Panchi, Song Kaoping, Yang Erlong. Controlled-rotating gate-based quantum neural networks model algorithm with application[J]. Control and Decision, 2011, 26(6): 898—901.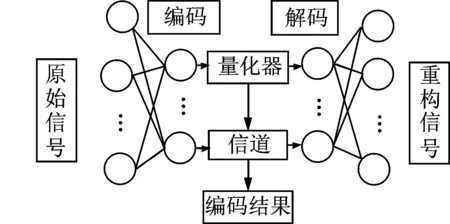

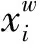
3 基于自适应学习量子神经网络压缩方法

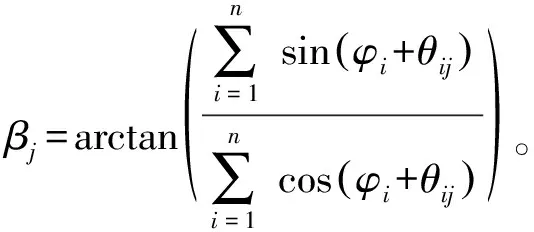

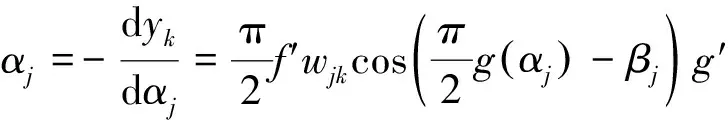


4 变速箱振动信号压缩应用




5 结 论

