利用混沌信号降低Cuk变换器的电磁干扰

国网安徽省电力有限公司亳州供电公司 胡 帆 张博博 尚广超

1.引言

近年来，我们面对新技术革命的浪潮，云计算、大数据、物联网、智能电网建设和新能源发电在全国迅猛发展，尤其是分布式发电、用户需求侧电能质量等新技术的持续推进，电网电源、运行方式、电网拓扑与负荷特性发生了巨大的变革，由此产生的电能质量问题也日益引起业界的广泛关注，成为热点。电能质量限值的确定主要考虑了电能质量与电磁兼容的关系。满足电能质量的要求依赖于电磁兼容的控制，也就是说，在电磁兼容良好控制的基础上，才可能从技术经济上实现电能质量的控制目标，电磁干扰的问题再一次成为各学者研究的一个重点方向[1]。开关电源由于其高可靠性、高效率以及体积小等优点得到了广泛利用，然而同时人们又被开关电源的电磁干扰问题所困扰。混沌信号具有内在随机性，且其功率谱较周期信号更宽，在一定频率范围内呈连续分布[2]。所以，在开关电源电路总能量一定的前提下，利用混沌信号的宽频谱来代替周期信号的离散频谱，可以降低谱峰，从而起到降低开关电源电磁干扰的效果。本文选用新兴的经典混沌电路“蔡氏对偶电路”作为信号源，首先对其电路及其混沌工作状态进行了简单的介绍，并验证了混沌信号的内在随机性，且在此电路基础上得到其输出的混沌信号，然后给出一种信号转换方法，得到可用于控制变换器的混沌调制信号，最后选用Cuk型变换器作为研究对象，建立可视化仿真，使Cuk变换器工作于混沌调制模式下，证实了利用混沌信号来降低开关电源电磁干扰的可行性。

2.蔡氏对偶电路

蔡氏对偶电路是与典型的混沌电路蔡氏电路在结构上完全对偶的一种自治混沌电路，由于其结构简单、电路所用元器件较少，所以具有很大的研究及利用价值[3]。蔡氏对偶电路由一个线性电阻、两个电感、一个电容和一个非线性电阻原件组成。

在不同的电路参数下，蔡氏对偶混沌电路可以有不同的工作状态，当逐渐改变电路的参数时，电路可以从稳定工作状态依次向单倍周期状态、多倍周期状态、单涡卷混沌状态、双涡卷混沌状态过渡[5]，本文主要利用了电路的双涡卷混沌输出。

通过分析蔡氏对偶混沌电路双涡卷混沌状态下的相图与时域图，可以得到混沌信号峰值电压数值、相邻峰值电压时间间隔、过零电压时间间隔具有高度的不确定性，这恰恰反映了混沌信号的内在随机性，正是由于混沌信号的这个特点，我们可以把混沌信号用于降低Cuk变换器的电磁干扰。

3.Cuk变换器的混沌控制方法及仿真

要实现Cuk变换器的混沌控制，首先需对蔡氏对偶混沌电路建立可视化模型，从中得到可利用的混沌信号，结合蔡氏对偶电路的映射动力方程等生成混沌调制信号，最后利用得到的混沌调制信号实现对Cuk变换器的混沌控制。在仿真过程中，利用到四阶“龙格库塔”算法对电路的参数进行计算，“龙格库塔”算法是一种“高精度单步算法”，其一般公式为：

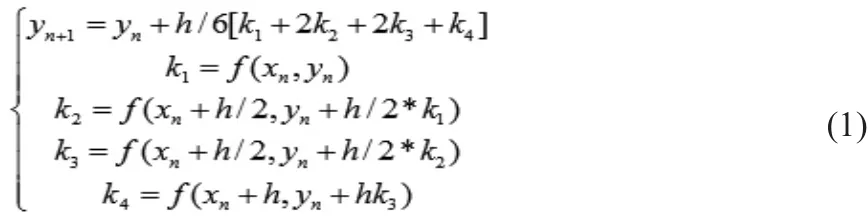
该算法计算后所得结果具有四阶精度，而且编程比较简便，可以满足仿真需要。

3.1 混沌控制方法及可视化仿真图

首先，蔡氏对偶混沌电路的状态方程如式(2)所示[6]，经过整理及变量代换，可得状态方程式(3)[7]：

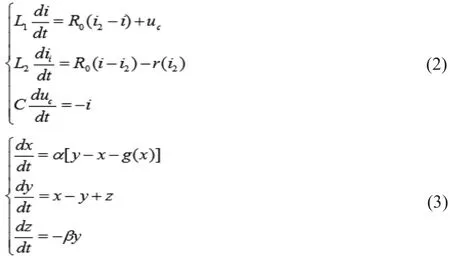
根据式(3)，建立蔡氏对偶电路的可视化模型如图1所示。

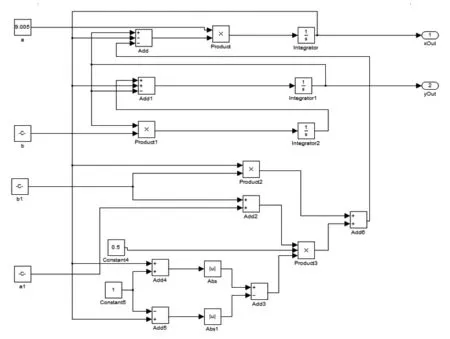
图1 蔡氏对偶混沌电路的simulink模型

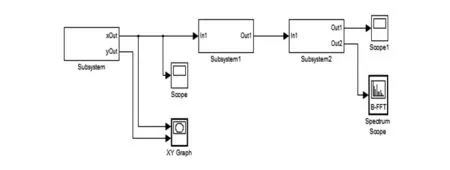
图2 Cuk变换器的混沌控制总图

利用已建立的蔡氏对偶混沌电路仿真可以得到电路输出的混沌信号，然后结合simulink中的Zero-Order Hold模块、sign模块、Random Integar模块、BPSK模块等实现信号的转换，进一步通过Fcn模块、Sign模块等生成混沌开关调制信号。其中Fcn模块是得到混沌开关调制信号的关键部分，该模块需要自己定义和设置生成混沌调制信号所需要的数学模型，此处混沌调制序列的生成是基于蔡氏对偶混沌电路的映射动力方程，因此需要将蔡氏对偶电路映射动力方程的数学表达式定义到Fcn模块中。

另可知Cuk电路的状态方程[8]：

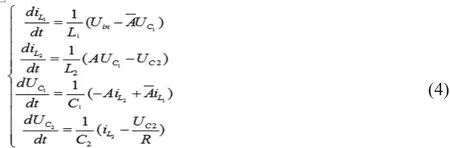
其中是输入变量是输出变量。

由Cuk电路的状态方程可以建立其可视化仿真模型。然后，利用利用simulink仿真软件中的子系统模块对蔡氏对偶混沌电路仿真部分、混沌开关调制信号生成部分、Cuk电路仿真部分三部分进行封装，并在需要的地方接上Scope模块、XY Graph模块、Spectrum Scope模块，用来观察电路相应部位的相图、时序图以及频谱图，这样就得到了Cuk变换器的混度控制总图，如图2所示。

3.2 仿真结果

利用仿真电路，可以得到Cuk电路在周期PWM触发模式下以及混沌调制信号模式下的电流波形图。

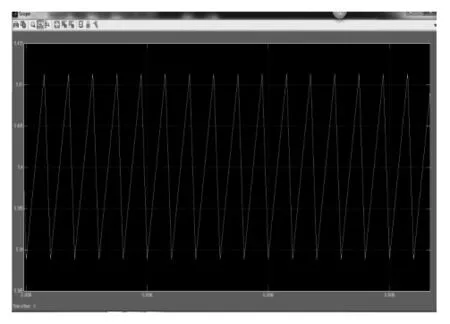
图3 PWM模式下的电流相图

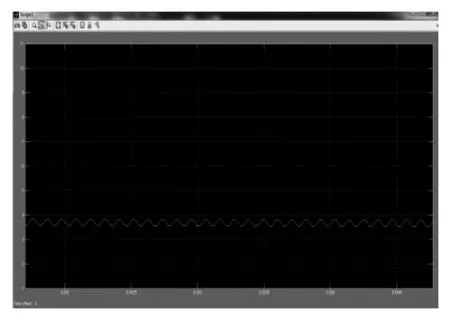
图4 混沌控制下的电流相图

在电磁干扰的产生过程中，对谐波干扰起主导作用的是电感电流，因此，降低开关电源的电磁干扰，主要是抑制电感电流产生的谐波[9]。而在电流谐波中，奇次谐波分量占主导，偶次谐波分量可忽略，即对开关变换器电磁干扰的抑制，实质上是对电感电流的奇次谐波的抑制[10]。由图3、图4可观察出混沌调制信号模式下电路的电感电流频谱在各奇次谐波处明显得到了拓宽,同时相比标准PWM周期模式下的频谱谐波最大幅值，混沌调制模式下的频谱谐波最大幅值也有一定程度的削弱。对比混沌调制模式与标准PWM模式下的奇次谐波幅值，可得混沌调制模式较标准PWM模式下的谐波减小值如表1所示：

表1 混沌控制模式较PWM模式下谐波减小值

由图9、图10、表1可知，混沌调制模式能减小频谱中的谐波峰值，频谱在所有谐波处都得到了扩展，频谱几乎是连续的，这样在总能量一定的前提下，频谱最大谐波幅值降低了，从而相应的降低了电路的电磁干扰水平。

4.结论

混沌信号具有内在随机性，其频谱几乎是连续的，利用混沌的这个特性，可以降低开关变换器的电磁干扰。本文利用一种新型的混沌电路-蔡氏对偶混沌电路，对其进行建模分析，验证了混沌信号的内在随机性，并得到其输出混沌信号，在此基础上给出了一种方法对该信号进行转换，得出混沌调制信号，进一步利用得到的混沌调制信号对Cuk电路进行控制。仿真结果表明，利用混沌控制方法，成功地扩展了电感电流的频谱，降低了各次谐波峰值的幅值，因此可以利用混沌信号用来降低开关电源的电磁干扰。人们一直被开关电源的电磁干扰问题所困扰，这种从源头上来降低开关电源电磁干扰的方法具有切实的可行性及广阔的研究前景，深入对利用混沌信号降低开关电源电磁干扰的研究，发掘更多更高效的混沌信号用来降低开关电源的电磁干扰，以及如何将这门技术运用于开关电源的实际生产是接下来的研究需要注意与解决的问题。

[1]张新国,马义德,李守亮.非线性电路:基础分析与设计[M].北京:高等教育出版社,2011:125-131.

[2]金爱娟,徐向丽,李少龙.PWM Buck变换器电容引起的混沌及其控制[J].电源技术,2015(01):141-143.

[3]季清,阮新波,叶志红.电流临界连续模式Boost PFC变换器最恶劣传导电磁干扰频谱分析[J].中国电机工程学报,2013(24):32-41.

[4]刘崇新.蔡氏对偶混沌电路分析[J].物理学报,2002,51(6):1198-1202.

[5]孙会明,陈薇,孙龙杰.Buck变换器的分数阶仿真模型与混沌分析[J].现代电子技术,2014(24):154-160.

[6]刘宏达,刘建,罗耀华.Cuk拓扑的Simulink仿真模型[J].应用科技,2004(04):38-40.

[7]丁敏.电磁干扰及其抑制措施的分析[J].科技传播,2014(16):67-68.

[8]Laxman Solankee,Laxman Solankee,Ashfaque Khan.EMI Reduction in Switching Power Converter by Using Chaotic Frequency Modulation Technique[J].Contemporary Engineering Sciences,2012(5),33-47.

[9]贾金钟.开关电源的电磁干扰分析[J].电子制作,2014(07):216-217.

[10]邓重一,龚昌来.混沌映射抑制Buck变换器电磁干扰的研究[J].低压电器,2009(07):46-50.