核电厂寿期管理经济性模型的参数灵敏度分析

吕方明

(中核武汉核电运行技术股份有限公司，武汉 430223)

美国EPRI从1980年开始研究寿期管理(Life Cycle Management, 简称LCM)技术在核电厂的应用问题。LCM是对老化管理和经济计划的整合，在保障设备性能和安全性的前提下，通过对设备的运营、维修和服役寿命的优化，最终实现核电厂投资收益最大化。

LCM的核心工作是针对设备存在的关键老化问题，制定多个长期的LCM计划，通过一定的计算模型分析各计划的经济性，为核电厂的决策提供定量的参考。考虑到货币价值的长期波动，一般使用净现值(Net Present Value, 简称NPV)方法计算各计划的成本费用[1-3]。鉴于LCM计划的长期性，NPV计算式中的参数值往往是对未来的预测值，存在一定的不确定性，当这些参数的取值发生变化时，必然会导致NPV计算结果的波动。因此，本文将使用参数灵敏度分析的方法研究各参数的变化对NPV计算值的影响，为制定可靠的LCM计划提供理论依据。

1 净现值模型

LCM计划的经济性分析中通常包含两种费用：成本和效益。成本主要是核电厂执行预防性维修(Preventive Maintenance,简称PM)、纠正性维修(Corrective Maintenance,简称CM)活动以及产能损失(Lost Power Generation,简称LP)等发生的支出费用；效益是核电厂执行重大改造/更换后，机组功率得到提升，机组能够更多地生产电力而获得的额外收入。

(1)CM成本是电厂在纠正设备失效时发生的费用，计算式为

(1)

式中CCM——纠正性维修总费用；CCMi——第i种失效模式的纠正性维修总费用；Fij——计算时间区间j内第i种失效模式的失效率。

(2)产能损失是指非计划停机(失效或计划工期延长)期间机组不能按计划发电造成的收益流失，计算式为

(2)

式中CLP——总的产能损失；CLPF——设备失效造成的产能损失；CLPT——重大改造/更换或大修计划工期延长造成的产能损失；CFj——机组在计算时间区间j内的能力因子；Fij——计算时间区间j内第i种失效模式的失效率；Ti——第i种失效模式的维修工期；Cp——上网电价；Pe——机组额定功率；ti——维修活动i(重大改造/更换或大修)工期延长的时间。

(3)电厂在实施重大改造/更换等维修活动后，机组的额定功率得到提升，由此带来额外的收益，计算式为

(3)

由此，LCM计划中的年度总成本或计算时间区间内的总成本可表示为

Ctotal=CPM+CCM+CLP-CPC

(4)

式中CPM——预防性维修成本。

考虑到电厂剩余寿命期间货币价值的波动，使用净现值方法将分析日之后的费用折算为当前货币价值，如式(5)所示[3]。

(5)

式中 NPV——评价区间上LCM成本净现值；j——成本分析的年度；Cj——第j年的成本；d——贴现率(货币成本)；k——通货膨胀率+真实浮动率；tj——产生成本的时间；tNPV——计算NPV的时间。

2 参数灵敏度原理

灵敏度分析方法就是当各因素在基准状态附近波动时，分析系统特性的变化情况，确定各因素对系统状态的影响程度。该方法的基本分析步骤如图1所示。该方法的分析过程是：保持其他参数不变，改变某个参数的数值，观察NPV计算值的变化情况。然后，再保持其他参数不变，改变另外一个参数的数值，观察NPV计算值的变化情况。这样，依次可以观察到每个参数的变化对NPV计算值的影响情况。最后，比较各参数的变化对NPV计算值的影响，确定出各参数的灵敏度。具体的分析过程可以参考文献[4]，这里不再赘述。

图1 参数灵敏度分析步骤

3 计算和讨论

以年度j发生的NPV为对象说明参数灵敏度分析的过程。由式(1)至式(5)可得第i种失效模式第j年度NPV值：

(6)

具有预测性质(不确定性)的参数有：失效率Fi、上网电价Cp、能力因子CFj、贴现率d、通货膨胀率/真实浮动率k，需要对这些参数的灵敏度进行分析。其他参数称为工程参数，其数值见表1。

表1 电厂某项工程中的工程参数值

将工程参数值带入式(6)得

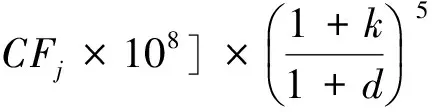
(7)

式(7)中，不确定性参数的基准值和变化范围如表2所示。表2中，k和d的基准值参考了文献[3]。

表2 参数的基准值和变化范围

其他参数取基准值并且保持不变，各参数在表2所示取值范围内变化时，其与NPV的函数关系为：

NPVFi=2 697.3Fi+2 108.9

(8)

NPVCP=6 532.4Cp+227.16

(9)

NPVCFi=2 689.8CFj+227.16

(10)

NPVk=12 203k+2 148.4

(11)

NPVd=-11 535d+3 552.9

(12)

根据式(8)～式(12)，使用式(13)可以计算各参数的灵敏度函数：

S(ak)=|dφ(ak)/dak|×(ak/S)

(13)

(14)

(15)

(16)

(17)

(18)

式(14)～式(18)灵敏度函数曲线如图2所示。

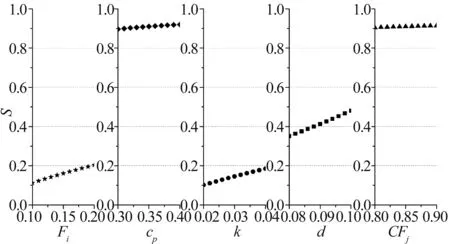
图2 各参数的灵敏度函数曲线

各参数取其基准值并带入式(14)至式(18)中，得到各参数的灵敏度因子，分别为：RFi=0.16；RCp=0.91；RCFj=0.91；Rk=0.15；Rd=0.41。灵敏度因子的含义(以RFi为例)为：如果失效率Fi选取的基准值与真实值相差10%，那么由此造成的NPV的计算值就会与实际值相差1.6%。基于此，如果上网电价Cp、能力因子CFj、通货膨胀率/真实浮动率k和贴现率d选取的基准值与真实值相差10%，那么，由此造成NPV的计算值就会与实际值相差9.1%、9.1%、1.5%、4.1%。总之，上网电价Cp和能力因子CFj的选取对NPV计算结果影响最大，贴现率d的影响较大，而失效率Fi和通货膨胀率/真实浮动率k的影响较小。

这些结果是建立在表1所述工程数据基础上的，当改变工程参数值时，参数的灵敏度因子可能会有所不同。主要的工程参数有：机组额定功率、CM工期和大修延长时间。通过改变这些工程参数的大小来考察上述参数灵敏度因子的变化情况。新的工程参数值如表3所示。

表3 新的工程参数值

改变这3种工程参数的情况下，前述5个不确定性参数的灵敏度因子的分布见图3～图5。

由图3至图5可以看出，工程参数的改变对上网电价Cp和能力因子CFj的灵敏度有一定影响，并且，这两个参数的灵敏度最大，变化范围为0.8～1；贴现率d的灵敏度较大，约为0.4；失效率Fi和通货膨胀率/真实浮动率k的灵敏度最小，小于0.2。然而，需要注意，当纠正性维修工期较大(如大于8天)时，其对失效率Fi的灵敏度因子的影响不容忽视。其原因是，相对于其它情况，此时纠正性维修导致的产能损失较大，与NPV总成本之间已经具有可比性。而在其他多数情况下，纠正性维修工期很短，甚至不存在产能损失。

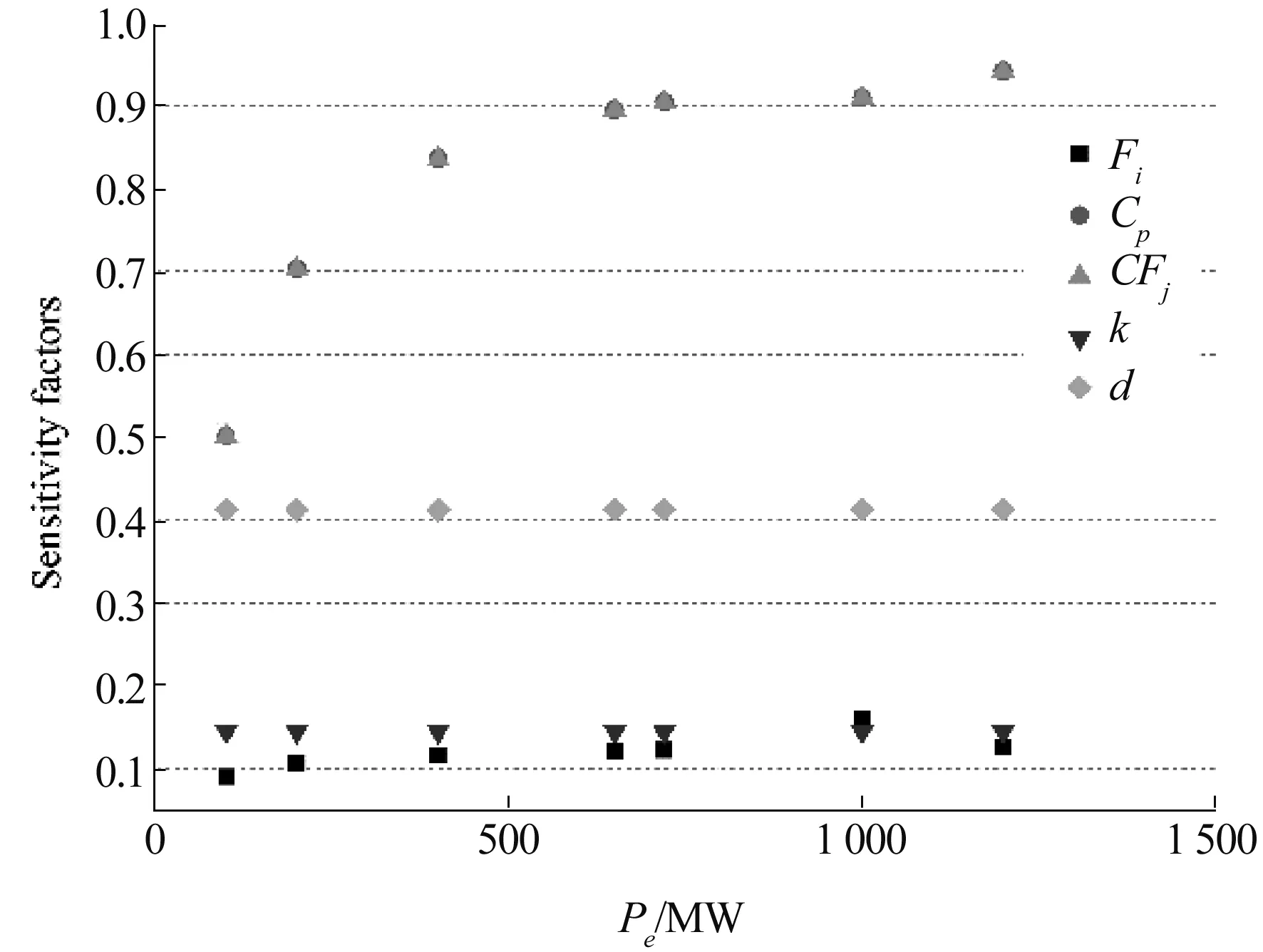
图3 机组额定功率对灵敏度因子的影响

图4 纠正性维修工期对灵敏度因子的影响

图5 维修工期延长对灵敏度因子的影响

4 结语

(1)在对核电厂设备的LCM计划做经济性分析时，有必要对具有不确定性的参数做灵敏度分析，应尽量确保灵敏度较高参数基准值选取的准确性。

(2)在NPV模型中，上网电价Cp和机组能力因子CFj的灵敏度最高，变化范围为0.8～1；贴现率d的灵敏度因子较大，约为0.4；失效率Fi和通货膨胀率/真实浮动率k的灵敏度最低，小于0.2。

(3)当纠正性维修工期较长(如大于8天)时，其对失效率Fi的灵敏度因子的影响不容忽视。

参考文献：

[1] EPRI TR106109, Nuclear Plant Life Cycle Management Implementation Guide[R]. 1998.

[2]EPRI TR-1007931, Life Cycle Management Economic Tools Demonstration Risk-Informed Long-Term Planning for Equipment[R]. 2004.

[3]EPRI TR-1003061, Proceedings of 2001 Workshop on Life Cycle Management Planning for Systems, Structures, and Components[R]. 2001.

[4]吕方明. 汽轮机转子低周疲劳寿命评价关键技术问题研究[D]：武汉：华中科技大学，2014.