3-RPS并联稳定平台设计与仿真研究

张峰，贾银亮，张弛宇，梁康武

(南京航空航天大学 自动化学院，江苏 南京 211106)

0 引言

随着我国军事科技的发展，舰载平台机构也在飞速发展。舰船在海面上行驶，不可避免发生不稳定运动，会对舰船上摄像系统的正常工作产生不良影响。因此需要一种稳定平台来隔离舰船的不稳定运动，从而保障摄像系统的稳定。

目前采用的机械稳定平台，多为传统的二、三轴串联转动平台。如陕西某公司研制的舰载X-Y型两轴稳定平台，利用惯性导航设备检测舰船摇荡参数，通过伺服系统分别驱动横摇轴、纵摇轴使平台向载体转动相反方向旋转，从而保证载体方位轴始终垂直指向大地[1]。南京某大学研制的船载卫星通讯系统稳定平台，采用三轴(方位、横滚、俯仰)稳定、两轴(方位、俯仰)指向的稳定系统结构[2]。这类平台是一种集光机电一体的现代化设备，在飞行器、舰船等领域有着广泛的应用，当作为稳定平台使用时，只能隔离转动[3]。并联平台也可以作为舰船的稳定平台来使用。并联稳定平台具有负载大、精度高、响应速度快等优点，在隔离舰船的转动同时可以部分补偿舰船的垂荡运动。

如图1所示，舰船在海上航行存在6种运动，即X、Y、Z三轴上的位移和绕三轴的旋转，其中绕X轴作旋转运动的横摇、绕Y轴作旋转运动的纵摇和沿Z轴作上下运动的垂荡对船舶影响最大。3-RPS并联机构具有3个自由度，可以用于隔离舰船的横摇、纵摇和垂荡，且结构简单、制造容易、适用于多种场合，因而引起人们的广泛关注[3]。

所设计的3-RPS并联稳定平台，可以补偿舰船横摇角和纵摇角，由于受到舰船空间限制，并联稳定平台尺寸有限，可以在一定范围内补偿舰船的垂荡运动。

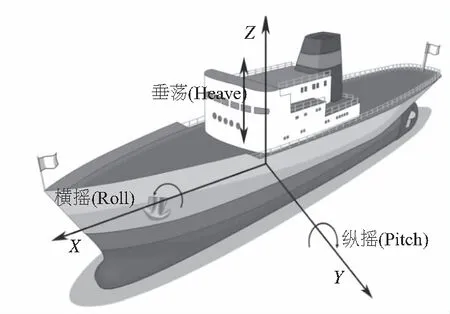
图1 舰船六自由度运动示意图

1 3-RPS并联稳定平台的设计

建立3-RPS并联稳定静平台坐标系和动平台坐标系，3-RPS并联稳定平台，包括动平台(以B标识)、定平台(以A标识)、连接动平台与定平台的支链、动平台与支链串连的球面副(S)和移动副(P)及支链与定平台相连的转动副(R)[4]。其中动、静平台中心点以OA、OB标识。通过控制3个支链的移动副的伸缩，可以实现绕X轴、Y轴的转动和沿Z轴移动[5-6]，如图2 所示。

所设计的稳定平台针对如下场合：舰船参数、船横摇参数、船舶纵摇参数见表1，三级海况下的随机海浪主要参数设置如表2,其中浪向角范围为0～π，通过Maxsurf软件进行舰船横摇、纵摇和垂荡仿真，通过MATLAB对仿真结果进行相应处理，可以得到横摇角度在-8°～+8°范围之间，纵摇角在-1.6°～+1.6°范围之间,垂荡在-0.6 m～+0.6 m。

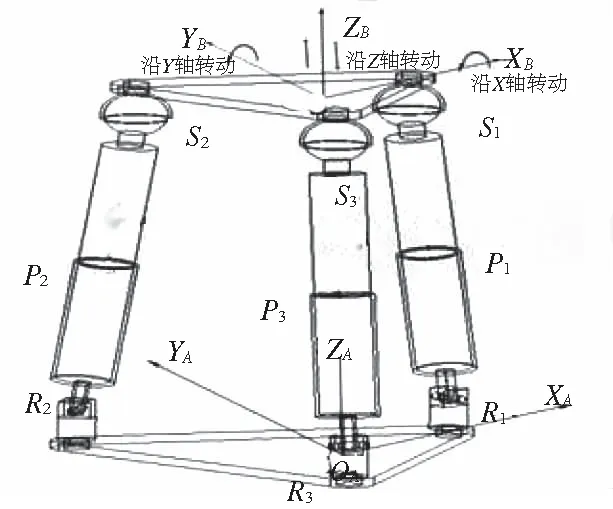
图2 三自由度并联稳定平台动静坐标系

表1 舰船参数 m

表2 海况参数

设计对应的3-RPS并联稳定平台，需要满足机械结构绕X轴角度范围，绕Y轴角度范围大于舰船横摇角度和纵摇角度范围的要求。

在SolidWorks中建立了3-RPS并联稳定平台模型，根据搭载的仪器设备需要，静平台外接圆半径取rA=173.21mm，动平台取rB=127.01mm，移动副中上下支链长度均取225.78mm，移动副伸缩运动中最小长度lmin取305.80 mm，最大长度lmax取451.60mm。根据搭载舰船尺寸的需要，动平台中心点OB在Z轴上的运动范围取302.30mm～449.20mm。调节3-RPS并联稳定平台模型运动关节，模仿运动，确保设计的并联稳定平台绕X轴和Y轴运动的角度范围大于舰船横摇角度和纵摇角度的范围。

工作空间分析是并联稳定平台研究的重要内容[7-8]。3-RPS并联稳定平台工作空间分析是基于舰船横摇角和纵摇角限制下，在MATLAB中，利用 3-RPS并联稳定平台尺寸参数和反解理论，绘制出的工作空间。即，在此工作空间内的每一点均可在横摇角和纵摇角度范围内自由转动动平台。其中3-RPS并联机构反解公式为：

式中欧拉角(α,β,γ)定义为先绕X轴旋转α，再绕转动后的Y轴旋转β，再绕转动后的Z轴旋转γ。上式为OB在静坐标系(建立在定平台A下的坐标系)下的位置坐标(AxOB,AyOB,AzOB)和位姿状态欧拉角(α,β,γ)反解得到3个支杆长度l1，l2，l3的运算关系式。再根据杆长的最长最短约束和转动副、球面副的转角约束，最后再根据舰船的横摇角在-8°～+8°范围之间，纵摇角在-1.6°～+1.6°范围之间的限制条件，绘制出满足舰船横摇角,纵摇角度范围工作空间，如图3所示。从图3中可得工作范围内OB在Z方向的移动范围为319.30mm～432.30mm，所以3-RPS稳定平台的垂荡最多可补偿距离为113.00mm。

图3 3-RPS在舰船上的工作空间视图

2 3-RPS并联稳定平台的动力学仿真

SimMechanics是MATLAB的建模仿真和分析的软件包，扩展了Simscape在三维机械系统的建模能力，可以用于开发机械手臂、医疗设备等机械系统，可以广泛应用于汽车业、航空业、国防和工业装备制造业[9-12]。

在Simulink中利用SimMechanics工具包，把相应的刚体和关节部件组建成3-RPS并联稳定平台的仿真模型框架[13-15]。

首先以3-RPS并联稳定平台静坐标系和动坐标系为基准，并根据尺寸参数配置3-RPS并联稳定平台Simulink机械模型各个组件的相应坐标系，在MATLAB中编写位置配置文件。模型的可视化图形如图4(a)所示。图中黑色球状物代表刚体的质心，并且每个刚体具有自己的坐标系，每个坐标系均参照图2所示静坐标系和动坐标系的建立，以方便利用3-RPS并联稳定平台位置反解公式。如图4(b)所示，为3-RPS并联稳定平台动力学仿真模型框图。

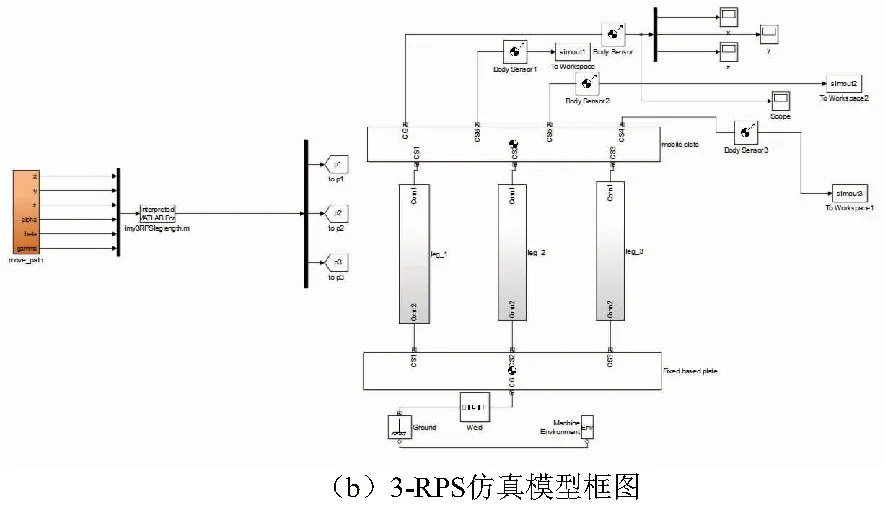
图4 3-RPS SimMechanics并联稳定平台模型

在MATLAB中对动平台中心点进行轨迹规划，设置动平台输入xOB=yOB=0，zOB=56.50 sin(2πt)+375.80,动平台姿态欧拉角全部取为0，则动平台保持水平并沿ZB轴以正弦规律进行运动。仿真曲线如图5所示，xOB和yOB始终为0，zOB以正弦信号规律进行运动。

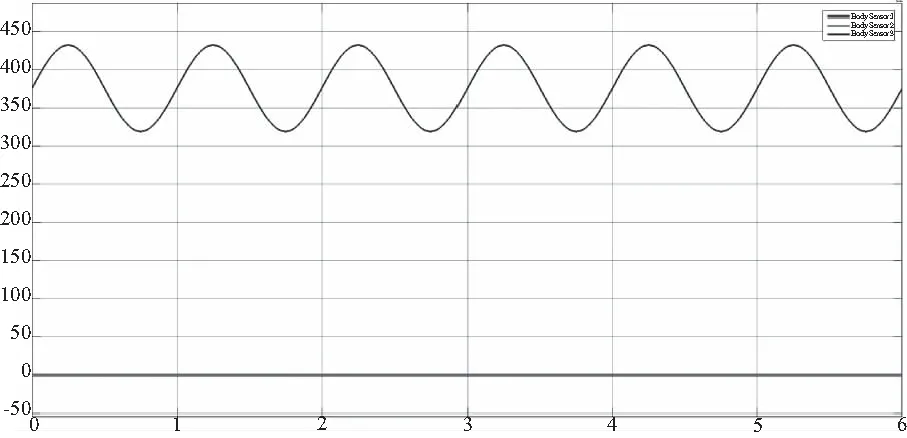
图5 动平台中心点运动仿真曲线

在MATLAB中设计相应的旋转角度补偿算法(根据绕坐标轴的旋转矩阵进行设计)，控制动平台下的支杆伸缩，使动平台绕XB旋转相应角度，令xOB=yOB=0,zOB=374.30mm，使动平台绕XB轴旋转以正弦变化规律，绕YB轴和ZB轴旋转0°，即α=6sin(πt)，β=γ=0 ° 。

同理令动平台中心点xOB=0，yOB=0,zOB=374.30mm，使动平台绕YB轴旋转以正弦变化规律，绕XB轴和ZB轴为0°，即β=6sin(πt)，α=γ=0°。

通过测量3-RPS并联稳定平台的动平台绕XB轴或YB轴旋转后动平台的3个顶点坐标，可得到动平台此状态下的单位法向量，进而可以计算出动平台绕XB轴或YB轴旋转的角度。动平台绕XB轴或YB轴旋转角度的变化曲线如图6。可知补偿舰船横摇或纵摇角度时，可以按照指定变化规律进行补偿。

上述仿真实验表明在外力的作用下控制3-RPS并联稳定平台的3个支杆的伸缩，可以控制动平台绕X、Y轴旋转和沿Z轴的伸缩运动，可针对舰船横摇、纵摇和垂荡进行补偿。进而在工作空间的范围内，可以对舰船的横摇、纵摇和垂荡进行补偿，从而验证了补偿的合理性。

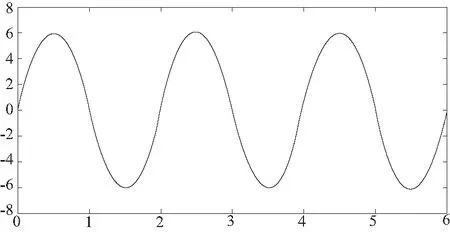
图6 动平台绕XB轴或YB轴角度变化曲线

3 结语

在舰船上应用并联摄像稳定平台的设计背景下，仿真舰船在海面上运动的横摇角和纵摇角，根据仿真出的角度范围研究了3-RPS型结构的并联稳定平台两维转动一维移动特性。在SolidWorks软件中建立3-RPS并联稳定平台三维模型，估计出相应的稳定平台相应尺寸等参数，仿真舰船横摇角和纵摇角限制下的工作空间，并引入SimMechanics机械动力学仿真技术作为舰载稳像方面的研究，通过仿真Z方向的运动和给定绕坐标轴旋转角度实验，验证所设计尺寸的3-RPS并联结构可以作为舰载稳定平台来使用。从而可以为并联稳定平台尺寸的设计提供技术上的支持。

[1] 刘晓. 并联 6-PUS舰载稳定平台机构学基础理论与实验研究[D]. 秦皇岛：燕山大学，2014.

[2] 詹银芳. 船载三轴稳定控制系统的研究与设计[D]. 南京：南京理工大学，2013.

[3] 罗二娟. 耦合型 3 自由度并联舰载稳定平台研究[D]. 秦皇岛：燕山大学，2011.

[4] 黄真，孔令富，方跃法. 并联机器人机构学理论及控制[M]. 北京：机械工业出版社,1997.

[5] Julien Mintenbeck, Ramon Estana. Design, modelling and control of a hyper-redundant 3-RPS parallel mechanism[J]. Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics,2010: 591-594.

[6] Dan Verdes, Sergiu-Dan Stan. Kinematics analysis, Workspace, Design and Control of 3-RPS and TRIGLIDE medical parallel robots.[J]. 2009 2nd Conference on Human System Interactions , 2009: 103-106.

[7] 张晓鹏. 基于Stewart机构的船载稳定平台的分析与设计[D]. 青岛：中国海洋大学，2013.

[8] Ciprian-Radu Rad, Sergiu-Dan Stan. Forward Kinematics and Workspace Analysis of a 3-RPS Medical Parallel Robot.[J]. Automation Quality and Testing Robotics,2010 IEEE International Conference, 4:132-137.

[9] 陈云. 基于SimMechanics和VRML的6-dof并联振动平台的运动仿真[D]. 吉林：吉林大学，2012.

[10] 王爱国，陈建伟. 基于MATLAB的3-RPS并联控制系统的仿真[J]. 工程设计学报,2016(2)：173-174.

[11] 安梓铭，朱大昌，李雅琼，等. 基于3-RPS型并联机器人模糊PID控制研究[J]. 制造业自动化，2014(15)：.15-18.

[12] YU Ling-tao, ZHANG Li-xun, ZHANG Nan,YANG Shuo. Kinematics Simulation and Analysis of 3-RPS parallel robot on SimMechanics [J]. Proceedings of the 2010 IEEE International Conference,2010: 2363-2365.

[13] Hannaneh Z. Arabshahi, Alireza B.Novinzadeh. Comparison of Motion Control Techniques for a 3RPS Parallel Manipulator[J]. Proceedings of the 3rd RSI International Conference on Robotics and Mechatronics,2015:302-304.

[14] 崔培. 3-RPS+RP 五自由度混联机械臂机构学分析与仿真研究[D]. 秦皇岛：燕山大学，2011.

[15] 苏士如. 并联四自由度舰载稳定平台特性及控制研究[D]. 秦皇岛：燕山大学，2014.