基于铁路施工图评审评价模型的原理与技术改进研究

王 超,卢文龙

(中国铁道科学研究院电子计算技术研究所,北京 100081)

铁路是我国重点发展的基础设施建设项目，铁路建设过程前期设计工作是铁路建设过程中的重点关注领域。在项目前期设计阶段，施工单位没有开工的情况下，施工图的设计质量对后续的进场施工以及工期安排有着很大的影响。面对现在工期日趋管理严格的情况，设计单位往往同时负责多个复杂项目的设计工作，建设单位对内部项目的质量把控与资金投向，都围绕在设计工作的涵盖范围之内。目前在基于施工图设计工作的评价体系的基础上，建立一套行之有效的考核机制来规范设计单位工作，对铁路建设前期工作的管理与推进具有非常重要的现实意义，也是铁路信息化工作领域推进的重要工作。工管中心施工图审核部每半年就要对所有在建高速铁路项目的施工图质量进行评审，结果作为考量设计单位工作的依据，评审结果优秀的单位在未来项目招标中占有优势。

近年来已经有很多学者与研究机构都以评价质量作为课题进行研究，目前广为采用加权平均算法(Weighted Average Method)对施工图完成情况进行评分考量，其评价算法特点为项目分类打分的基础上进行分值的评价与求均，进而分析出评价因素的长期趋势变化规律。优点在于只在结果计算一次加权平均，适用于快速评价内容涵盖简单的项目，过滤了主观因素对结果的波动影响，对各设计单位评价工作的考核结果较为折中。但由于高速铁路建设过程的多样性与施工技术水平的提高，尤其现在施工过程采用EPC方法分解桥梁专业、隧道专业、电力及牵引供电、站场改建等专业分类比较细的项目，设计单位出图的内容与复杂度几乎呈指数性提高，简单通过加权平均算法已经不能满足设计工作量的差异。

面对施工技术持续提高而产生的技术复杂性，在施工图评审过程研究出一种符合技术特点的评价模型，并以此为基础进行评价算法的改进。算法以项目负责单位对设计单位进行分类打分生成基准分值，创新性地加入了EPC专业因素作为影响参数，引入大数据模型作为辅助参数，以差分方程为基础来建立一套评价模型[1-2]。并首次应用在设计单位评价考核实际过程中，解决施工图审核过程中的复杂项目评审遇到的问题，并利用方差误差分析法过滤复杂项目下因素干扰，使得算法在评审复杂项目过程中更加准确，客观地反映设计单位施工图的评价质量，这在铁路设计与交付领域具有专业的独特性。

算法的关键技术在于其基础数据收集过程可结合历史数据归溯，搭建评价模型的验证数据进行回归验证分析，采用ANOVA方差分析方法对多个项目的评价结果与单个项目的评价结果作验证统计[3]。通过对比找到实际应用过程中对评价造成影响的关键性因素并作调整。在此基础上优化了算法，并进行过程中的分布校验验证，以保证最终结果准确。

1 评价算法介绍

依据中国铁路总公司关于印发《铁路建设项目勘察设计单位施工图评价办法》的通知规定，前期工作需要收集建设单位对设计单位的基础评分数据，通知内容对评分范围以及规则都作了严格的规定，建设单位按照扣分细则对负责项目进行评分操作，评分细则如表1所示，评分结果作为算法基础数据进行录入。

表1 建设单位评价打分细则

在一个完整建设周期内进行的施工图评价过程，是指建设单位对勘察与设计单位施工图阶段工作定期进行的评价，每半年为一个评价期。评价内容包括施工图提供、施工图质量、配合施工等，总分为300分。评分内容引入了分专业分阶段的概念，对桥梁、地质、隧道按专业标准进行评价，对预算、资金、现场配合按实际工作内容进行评价。细则表中1～3项为扣分项，主要体现发现的评审问题，为建设单位按实际情况填报。4～5项为加分规则，主要涉及技术方案优化、工程措施优化、结构安全优化中存在显著的工作业绩进行加分，加分最高为20分，扣分项由建设单位确定，加分项由工管中心施工图审核部确定。

针对以上分类分值原则，设计单位在同一时期负责多个项目的设计工作时，则采用综合评价分析来进行加权平均作为基准评价分值，加权公式为

F=∑(ai×bi)/n

(1)

式中，ai为各自项目的评价分数；bi为项目权重；n为权数，n为各项bi加和。其中项目权重bi值的制定规则按照项目的特点进行定义，国家重点建设项目，客专项目，国家政策支持的重点项目，则权重计为1.5；初步设计批复的静态投资额在50亿元以上的项目权重为1.2；初步设计批复的静态投资额在50亿元以下项目权重为1.0。

基础评价分值体现的是对单个项目的评分进行加权，针对于施工图评审过程中复杂项目的评审，则需要进行复杂分类下的基准公式计算来体现差异性。基准公式计算方法需要追溯2012年至2017年的所有评审历史数据。目前根据数据统计，设计院审核权重1.5以上重点建设项目为6个，审核权重为1.0以上的项目最多为58个。这里将样本分析的个数设置为8个，是体现重点项目的审核规范，同时在基准分析以及误差分析时，将样本个数扩展至61个，建立符合实际情况的数学分析模型。评价期基准分公式与计算方法如表2所示。

表2 基准公式计算方法

表2基准公式内参数：F为建设单位内各勘察设计单位评价分数；G为建设单位权重(铁路公司为1.2，客专公司为1)；K为所有建设单位对设计单位评价分数的平均值，K值在整个评价过程中单独进行计算。对此种算法的结果进行分析判断准确性，通过对工管中心历年评审基础数据进行收集与整理，在此基础上应用基准公式算法进行推演，对前三项扣分，中心确认加分与项目总分值分布特点进行验证，推演结果如图1所示。

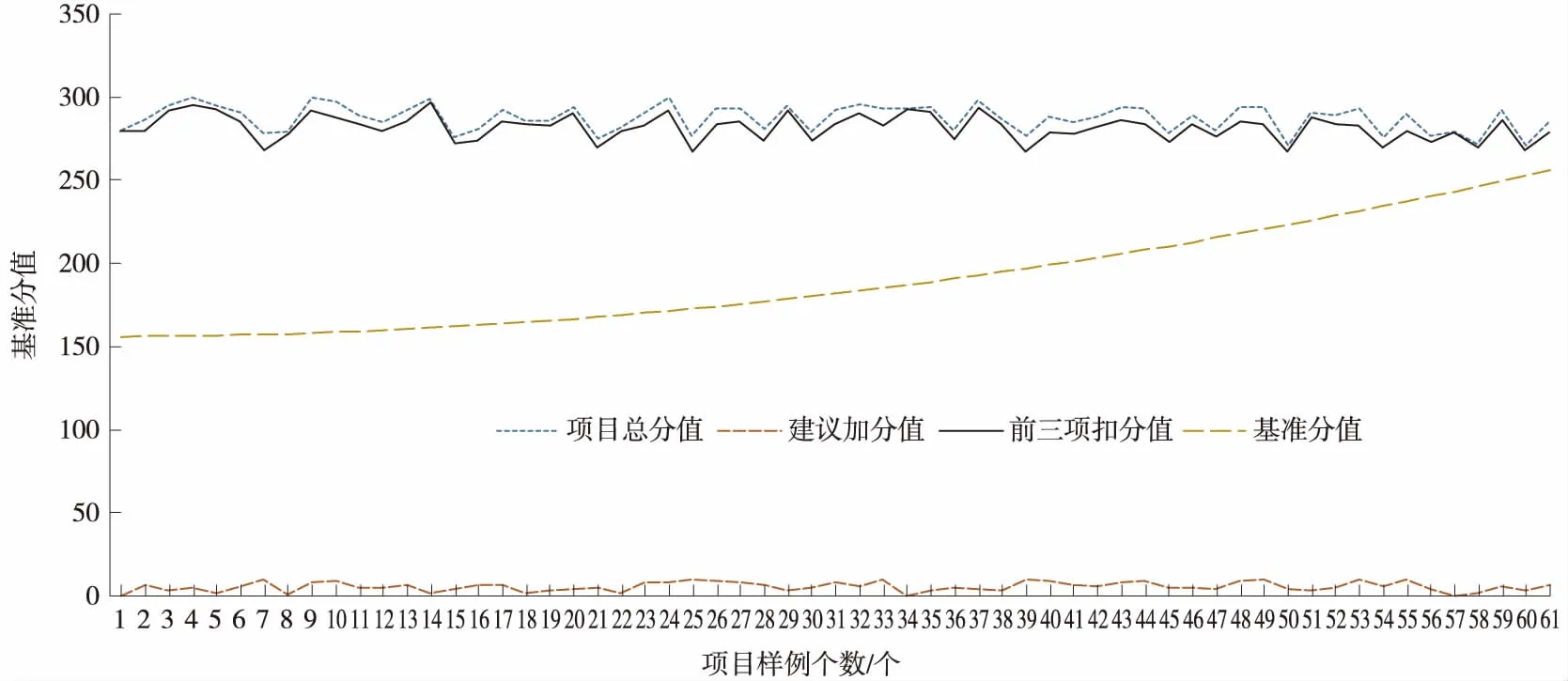
图1 基准公式算法验证分布

图1验证过程取样为大数据模型内累计项目典型数据，采样数据为61个典型项目的评审数据。对比图中分析结果线性变化趋势，其中前三项扣分值有很多在275～280分之间徘徊，并没有大幅波动，表现评分细则对评分进行有效的规范；优化建议加分值变化幅度较大，表明建设单位对项目设计评价有一定的主观性。同时看到建议加分的波动影响到最终总分值的结果较大。在此基础对多项目的评价工作进行分析，对于负责复杂项目设计工作的单位，工作量明显比负责单个项目的单位要多，而评价算法对于复杂项目的影响因素过滤较少。目前采用的算法针对复杂项目采用可调整的权重比，图中显示基准分值随着项目数目的增多有指数性的升高趋势[4]。针对基准分值的分布特点采用ANOVA方差分析方法建立模型。比对每个因子水平下得到的样本数据，考虑到权重值1.5以上项目的分析过程，将基准分值建立在8个以上项目的基础上，不考虑多因子的方差分析，将8个以上的项目推演公式代码。利用点状图分析误差的结果，找到最优的权重设置。将项目个数以2个作为基数进行权值代入公式计算，从而找到生成基准公式的规律，将权值与分值计算方法进行推演[5]，基准公式描述如表3所示

表3 权值设置与对应基准公式

表3中，F为扣分与加分操作后的总分值，K为各项目总分值的平均值。在多因子的方差分析中，项目的数目在评价过程中对整体结果有影响，会导致设计单位最终基准分值的较大变化，表示组间误差中只包含随机误差，这时组间误差与组内误差经过平均后的数值就应该很接近，它们的比值就会接近1。当项目的数目在评价过程中对整体结果有影响的情况下，在组间误差中除了包含随机误差外，还会包含系统误差，这时组间误差平均后的比值就会大于组内误差平均后的数值，它们之间的比值就会大于1[6]。这个比值大到某种程度时，就可以认为不同水平之间存在着显著的差异，也就是项目的数目对因变量有影响。

由于各种评价因素的影响，研究所得的数据呈现波动状。造成波动的原因可分成两类，一是测量环境中不可控的随机因素，另一类是研究中施加的对结果影响的可控因素。造成的误差会导致审价结果排名会有很大的变化，单一项目的分值过高会使评审结果影响较大。如果这种差异主要是系统误差，说明算法在多个项目评价中存在系统误差会对结果产生显著影响，针对此问题建立模型找出被检测的次数差异主要是什么原因引起，从而找到一个优化调整的算法来补充。

这里对权值参数R进行调整，以找到个体因素对整体结果影响最小的最优数，并对最终的评价结果引入一个基准分值进行调整。考虑到前期评价扣分值的随机性，采用点状图分布来解释误差的变化，如图2所示。

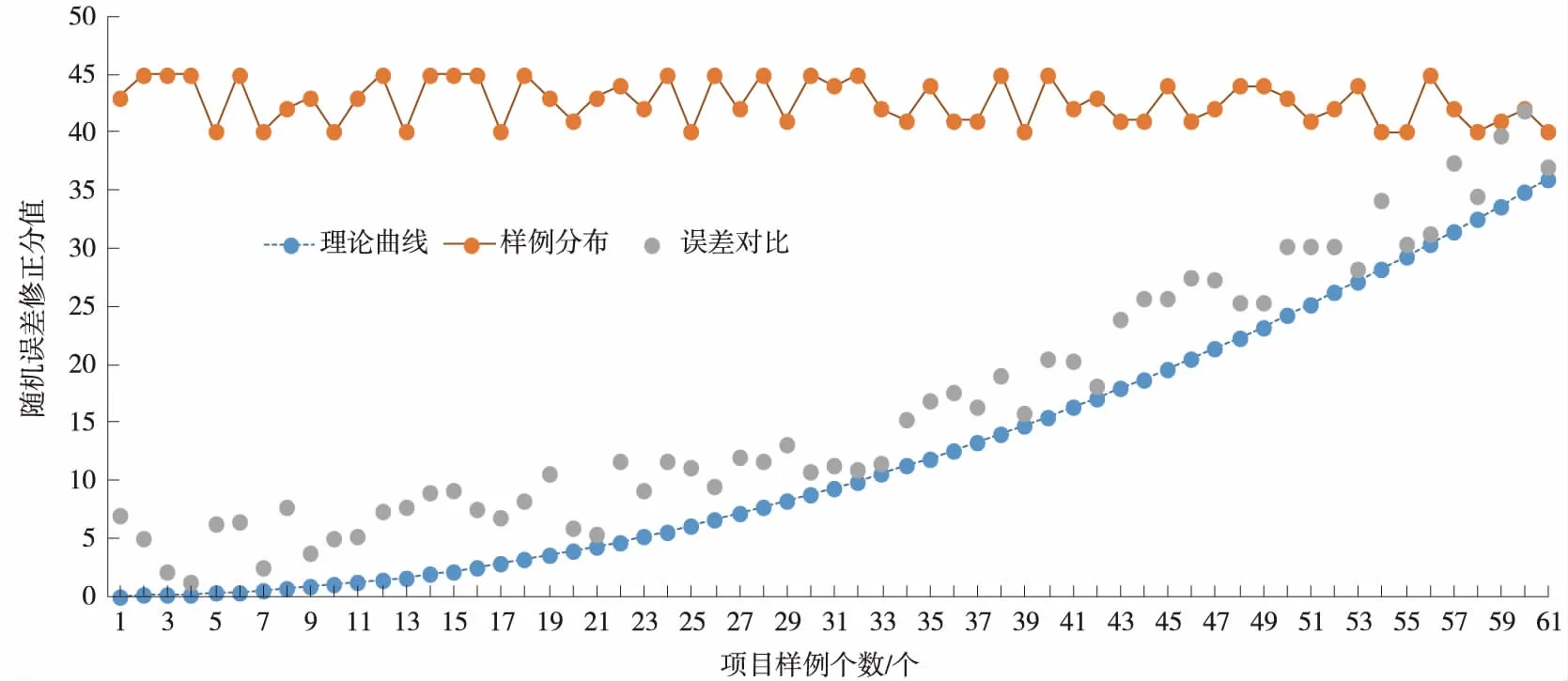
图2 多项目评价分值误差分析

图2显示理论方差标准值在总体结果中都是服从指数分布的，而误差样例结果呈随机分布并且始终大于理论曲线。误差对比曲线表现的是组间误差平均后的比值，曲线的变化情况是不规则的，表明因素的随机变化过程是不稳定的，并且随着项目数目的增多对评价结果造成影响的因素也会增多。这说明在实际的施工图评审过程中对多项目的评审工作，随着项目数目的增多以及评审因素的复杂，最终的评审结果会有一定程度的偏差。而最终的影响就是，当评审一家负责多个重点项目的设计单位时，评价结果会有失公正。

2 评价数学模型

针对于以上问题进行评价方法的改进，建立数学模型模拟评审过程中的各项因素，以及对结果产生的影响，从而在此基础上进行算法的模拟改进与验证。针对铁路评价行业特点和要求，差分区域的分析方法可以符合实际评审过程的模拟特点。差分区域分析方法是一种利用动态系统的拓扑理论来构造自然现象与社会活动中因素干扰的数学模型，其主要研究归纳分析因素对结果的影响因素和模拟操作过程，从而分析误差产生的原因和条件，找到符合实际过程中的变化规律[7]。差分数据模型由定性分析与定量研究的相互结合，定性分析主要考虑评价指标的完备性、针对性、稳定性、独立性等因素，主观确定影响因素和结构的过程。定量研究则是通过一系列检验，使评价体系更加科学和合理[8]。在差分区域方法中引入线性回归法进行定量的分析，并评价多个项目审核过程中的定性特点。在验证的计算过程作多元线性回归，并将结果与标准值的比较生成近似的描述公式，得到的结果如图3所示。

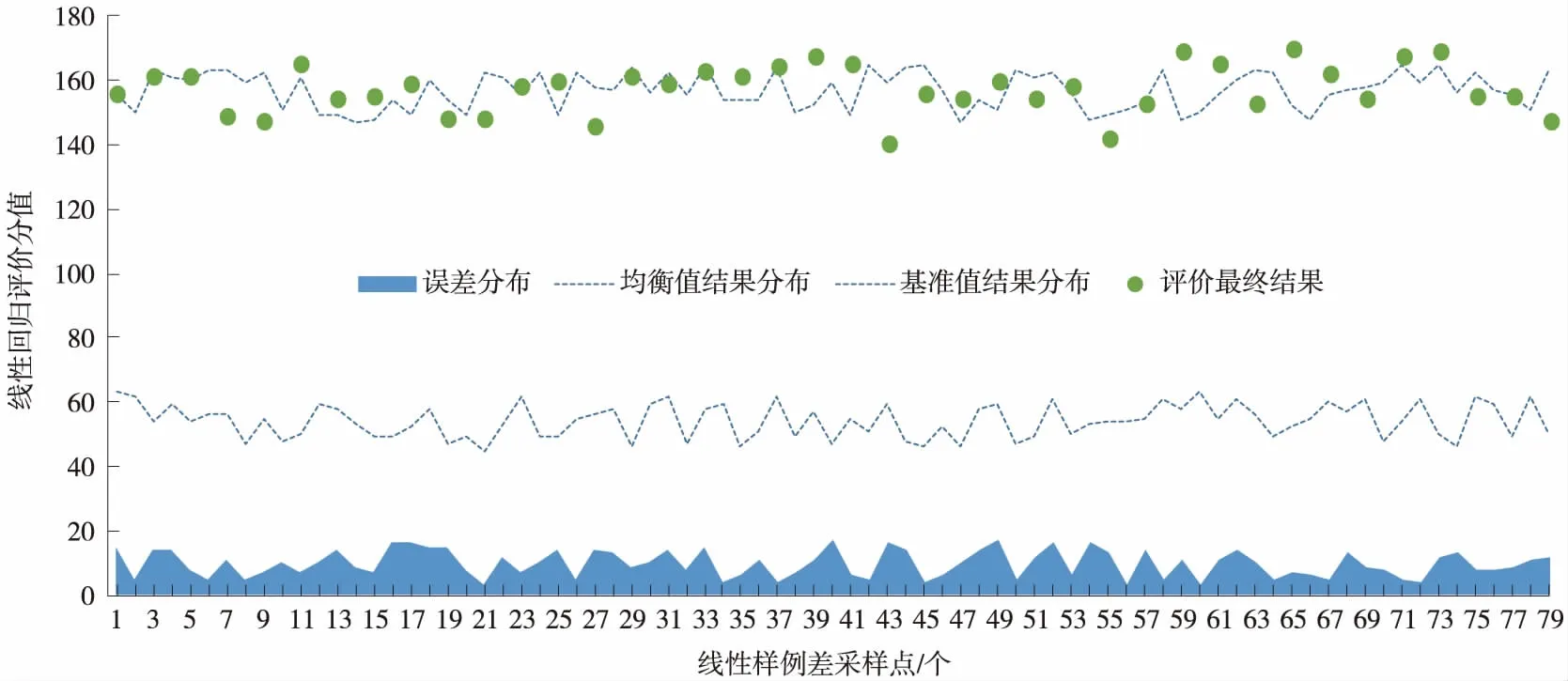
图3 线性回归结果分析

由数学模型生成的线性方程进行近似结果的描述，归结的R值为0.059 31，从图3中看到所有小于0的均衡分值都对结果的影响较小，而误差分布随着样例数据的增加稳定在一定的范围之内。基于差分区域归纳的线性模型通常由多个输入变量组成，对于给定的数据集，线性方程的属性在一定程度上反映了评价过程的特性，表明在此基础上进行的数据化模型可以反映真实过程[9]。在前面介绍的建设单位总体评价结果分析中，标准化管理与总分是呈随机分布的，所以要加入随机分布的影响因素以体现评审过程的中误差，这样建立起来的差分区域模型才能准确描述评审过程中的各项因素调整影响，将实际当中的权值参数与优化计算公式进行整理，并将上节介绍的组间误差平均后的比值进行对比，结果如表4所示。

表4 权值参数与误差对比

对结果进行线性随机分布的优化，找到M值最优的解，M值越接近1结果则越精确。在权值与误差平均比值的对比中观察到，样例扩展到8个以上的项目时，M值已经逐渐趋近于1，误差分布已经得到有效控制[10]。在差分区域模型里进行推演的规则条件下，实际上也就是检验具有同方差的8个正态总体均值是否相等，如果8个总体的均值相等，则可以推断8个以上的样本均值也会很接近，由此推演到多项目的情况评价算法可以参照表中的调整的基准分值公式的内容进行模拟。对项目样本计算结果进行权重值的分析，归纳出多个项目评审时采用的基准分值算法公式为

M=∑0.5(Fi×Gi)/N

(2)

式中，M为基准分值；F为建设单位内各勘察设计单位评价分数；G为建设单位权重；K为所有建设单位对勘察设计单位评价分数的平均值；N为权数，N为各项G权重之和[11]。

评价体系的建立是需要多方面的扩展，未来的评价工作机制会发生一定的调整与改变，例如项目的评审规范与分值制定都会产生变化。模型采用指标体系进行施工图评价体系调整，通过调整多指标因素来适应条件的改变[12]。

3 演化算法改进

通过模型的真实模拟，对复杂项目评价的算法优化已经可以将系统误差控制在合理的范围内，并分析出最优后的算法公式与权重分配。同时运用网络计量方法探索评价模型建立的基础数据构建，其主要研究对象是800个项目样本的评价数据，并建立大数据样本，进行均衡分值的计算[13]。分别计算某设计单位得分与所有设计单位得分平均值的差值。F平均值为某建设单位内所有勘察设计单位得分的平均值。M值以±4分为限，这里±4是将平均分值控制在一个合理的范围内。再分别计算某个设计单位在各建设单位的M值之和

X=∑(M×G)

(3)

所有设计单位在同一时期内得到最高基准分的分值作为均衡分补偿。由于系统误差不能完全获知，因此这种补偿并不完全。而加入基准分值对于结果的修正偏差具有校正作用，从而去除含有误差的测量结果[14]。基准分值的计算是在设计单位最高评价分值的基础上进行对比，并将所有设计单位的基准值与最高值作差，这样保证了基准值不会对最终结果造成太大影响。

基准值作为修正因子，在最终的评价结果中是体现差异的首要因素。通过修正因子或修正值已进行了修正的测量结果，即便其具有较大的不确定度，但仍然十分接近被测量的真值[15]。修正后的方差误差分布情况如图4所示。

图4 修正后的误差分布

由图4可以看到，虚线表示的差异更加趋近于实线理论值，误差对比曲线在随着样本数量增多的情况下没有产生大幅度的随机性变化，一直在稳定的区域范围内变化，图中误差对比曲线在项目复杂度增大的情况下也呈现平滑，明显消除了系统误差对最终评价结果造成的影响。最终证明了引入模型分析出的评价结果技术改进是有效的。

将评价模型与优化的计算方法进行实际情况的验证应用，将2015至2017年度的历史评价数据代入改进的算法中，结果表明复杂项目评价工作准确度上升了3.5%，涉及到的排名变化为一家设计单位。由于算法的复杂度与精确度提升，以前遇到的排名同分并列的问题也一并解决。经过核算，优化的算法在多样本与误差随机分布的条件下，将误差结果控制在合理的范围内，并解决了复杂项目评价下审核结果的有效。经过中国铁路总公司工管中心在2016年的实际推广，应用新型算法改进进行评价结果的辅助计算，结果证明使用改进后算法进行的评价能非常客观体现差异，同时各设计院的投诉建议也减少很多，由评价结果产生的排名公正有效，取得了很好的效果。

4 结论与建议

本文在大数据的基础上完成了施工图评价模型的算法改进，找到在复杂项目评价过程中对结果影响较大的因素，并采用线性回归方法验证误差存在的分布。通过基准分值作为优化因素进行调优，减少了在计算过程中的系统干扰误差，对整体评价体系验证起到了重要作用，并在最新的考核信息化工作中得到推广与应用。

鉴于针对评价工作的实际情况，建设单位在评价基础分值时也会存在主观意识的偏差，尤其在建议加分值和电子交付文件中体现的差异非常大。评价体系是关于复杂对象的多指标，多因素，多主体，多层次为特征的[16]，需要进行不断的探讨与优化。由于评价结果在施工图审核过程中的权威性，未来需要找到更加符合现实意义的数学模型，建立一个科学公正有效的多维度评价体系。

[1] 江杰，高超，虞丽娜.权值动态分配的加权平均法在姿态解算中的应用[J].航空制造技术，2016(11):106-109.

[2] 宋乾双，丁奇杰，冉维毅.BIM技术在结构施工中的应用[J].智能建筑与智慧城市，2016(2):78-80.

[3] 卢冶飞，孙忠宝.应用统计学[M].北京：清华大学出版社，2015.

[4] Chen Xiaohui， He Yifeng. Inference of high-dimensional linear models with time-varying coefficients[J]. Statistics， 2017：12-13.

[5] 闫志刚，杜立峰，王雪丽.基于突变级数法的绿色施工评价研究[J].铁道工程学报，2017，34(2):76-80.

[6] 陈正江，蒲西安.多元线性回归分析与逐步回归分析的比较研究[J].牡丹江教育学院学报，2016(5):131-133.

[7] 张家年，占南，李阳.基于网络计量学的网络课程评价方法研究[J].远程教育杂志，2015(1):101-102.

[8] 张生瑞，邵春福，严海.公路交通可持续发展评价指标及评价方法研究[R].中国公路学报，2005，18(2):74-78.

[9] 强保华，唐波，王玉峰.基于线性回归和属性集成的分类算法[J].计算机科学，2017，44(6):212-215.

[10] JB Corbets， CJ Willy， JE Bischoff. Evaluating System Architecture Quality and Architecting Team Performance Using Information Quality Theory[J]. EEE Systems Journal， 2017(99):1-9.

[11] 中国铁路总公司.铁总建设[2014]125号 铁路建设项目勘察设计单位施工图评价办法[S].北京：中国铁路总公司，2014.

[12] 仇志明.桥梁工程钢筋混凝土施工质量评价模型[J].铁道标准设计，2014(2):61-63.

[13] 中国铁路总公司工程管理中心.关于2016年上半年铁路建设项目施工图评价初评情况的报告[R].北京：中国铁路总公司工程管理中心，2016.

[14] 徐泽水.多属性决策的两种方差最大化方法[J].管理工程学报，2001，15(2):11-13.

[15] 朱小辉，陶卿，邵言剑.一种减小方差求解非光滑问题的随机优化算法[J].软件学报，2015:2752-2761.

[16] 何志工.铁路枢纽总图规划及其评价体系的思考[J].铁道标准设计，2012(12):5-8.

[17] 张明.铁路信息化评价考核指标体系研究[J].铁路计算机应用，2017，26(4):32-35.