一种支持范围查询的云数据空间索引研究

李剑锋,陈世平,段林茂,钮 亮

1(上海理工大学 管理学院,上海 200093)2(上海理工大学 光电信息与计算机工程学院,上海 200093)3(中国计量大学 经济与管理学院,杭州 310018)

1 引 言

移动互联时代,基于地理位置的移动应用程序(APP)产生了大量的多维数据,此类数据至少包括位置信息和时间戳两个属性.传统的关系型数据库在海量数据高效读取方面存在瓶颈,而分布式关系数据库在服务器间维护数据一致性等方面所付出的代价较高[1].

以Google公司提出的BigTable[2]技术为代表,产生了很多新的分布式云数据管理系统(CDM),如HBase和Cassandra[3]等.与分布式关系数据库相比,基于BigTable的CDM具有适用性广、可扩展、高性能和容错性好等特点.上述CDM使用Key-Value的方式来存储数据,具有高效的数据检索性能,原因主要有两点:1)每个Key-Value对被存储在多个服务器上;2)每个Key又会保留多个版本的值.其中,第一个特点有利于提高检索数据的效率,第二个特点降低了维护数据一致性的延迟时间.但由于BigTable在数据结构上的局限,这些云数据管理系统只能支持一些基本的操作,例如HBase的Put、Scan和Get操作并不直接支持多维查询.

针对上述CDM的原理和特点,本文提出了一个新的可运行在CDM上的多维索引HPR-index,该索引通过为每个桶PR四叉树的叶节点分配一个希尔伯特(Hilbert)键值来实现多维查询.本文的第一个难点就是如何避免查询结果中出现大量的冗余数据.如果地图被分成过多的网格,虽然不同网格包含数据量的差距会缩小,但同时会造成数据查询效率下降.因为对于一个空间范围查询而言,同样大小的空间内网格越多意味着需要查询的叶节点就越多,查询时间会相应增加.理想的情况是网格尽可能小的同时查询数据的时间越来越短.因此,对于CDM而言,如何划分地图网格的密度来达到两者的平衡至关重要.为解决这一难点,HPR-indexs索引采用平衡的桶PR四叉树来组织多维数据,每个四叉树的叶节点“管理”一个网格.采用桶PR四叉树的原因主要有两点:1)桶PR四叉树可通过分裂来达到网格大小和查询时间之间的平衡;2)与其他树结构如R树相比,桶PR四叉树的叶节点不互相重叠,这样就避免了从不同叶节点读取出大量相同数据的冗余问题.本文的第二个难点是如何设计网格的键值命名规则,使之在基于BigTable的CDM上实现高效的多维查询.本文根据上述CDM的两个特点,即系统具有高速的key-value查询效率,并通过字典顺序对键值(key)执行快速的Scan操作,利用Hilbert曲线的编码规则为每个网格命名唯一的Hilbert键值.建立并维护一张路由表,表中每个网格区域的键值与桶PR四叉树的叶节点一一对应.根据HPR-index的数据结构,定义了实现空间(二维)数据范围查询的算法以及插入和删除算法.

本文的贡献包括如下四点:1)提出了可运行在CMD系统上的空间索引结构HPR-index,该索引利用平衡的桶PR四叉树来组织空间数据,利用Hilbert曲线编码为每个网格命名唯一的Hilbert键值.HPR-index在数据均匀分布和数据偏斜的情况下均实现了高效的空间范围查询.HPR-index索引经过修改还可用于多维数据的范围查询和KNN查询;2)HPR-index高效地利用了CMD的特点,获得了较好的查询效率;3)根据HPR-index的原理,设计了新的空间数据的范围查询算法;4)与当前的多维索引技术相比,HPR-index具有维护代价低,实现方案简单,偏斜数据查询效率高等特点,且适用于HBase和Cassandra等CMD.

2 相关工作

2.1 树结构和线性结构

R树被广泛用于多维数据索引.R树兄弟结点对应的空间区域可以重叠,因此R树的查询效率大大降低.为了更高效地索引多维数据,产生了很多R树的变种,例如R+树,R*树等.其中R+树子树上的结点会频繁重新划分,插入和删除效率低.

四叉树是另一种索引多维数据的常用树结构.PR四叉树具有结构简单、等分数据空间、空间划分无重叠等优点.但当数据不是均匀分布而形成了集簇或聚集时,PR四叉树含有很多空的节点而变得不平衡,这种不平衡可通过把这些节点对应的块聚合成叫做桶(bucket)的更大的块而解决,即把分解方法变成只有当块内包含超过s个数据点时才分解,这里的s叫做桶容量,这种四叉树是桶PR四叉树(bucket PR quadtree)[4].桶PR四叉树经过改进可用于构建适合云数据管理系统的多维索引结构.

线性索引技术通过将多维数据降维到一维数据来进行索引,主要的技术有空间填充曲线,如Hilbert曲线和Z-order曲线.Hilbert曲线可以将高维空间中没有良好顺序的数据映射到一维空间,经过这种编码方式,空间上相邻的对象会邻近存储在一起,因此提高内存中数据处理效率.相对于其他多维线性化技术,使用Hilbert曲线编码在处理数据聚集的情况下具有优势.

2.2 多维索引相关研究

近年来,基于上述多维数据索引技术,如Quad-kd[5]等,在CMD上构建新型索引的研究越来越多.RT-CAN[6]在每个云节点的本地数据上建立R树索引,并动态选择一部分节点发布到全局索引.MD-HBase[7]是基于Hbase的数据管理系统,利用四叉树、k-d树以及Z-Order技术来索引多维数据.MD-HBase数据一致性问题的解决方案较复杂[8].KR-index[9]在CMD上实现海量偏斜数据(skewed data)的多属性查询.该技术采用R+树将数据划分为互不相交的矩形单元,这些矩形存在R+树的叶节点上.然后再将整个空间分成若干个互不相交的网格,利用Hilbert技术将这些网格进行编码,并将矩形单元与网格的相交关系记录到KeyTable表中.KR-index存在结点频繁重新划分、插入和删除效率较低等问题.本文提出的HPR-index吸收了KR-index的部分思想,采用桶四叉树结构来避免R+树的一些不足.M-Index[10]采用金字塔技术(pyramid-technique)将数据的多维元数据描述成一维索引.基于HBase的交通数据索引框架[11]利用z-ordering技术进行数据分区以支持高效的多维查询.M-Quadtree[12]支持多维空间查询,满足MapReduce并行化要求.DGFIndex[13]是一种基于分布式网格文件的多维索引技术,用来提升Hive的多维查询处理能力.数据多维去重聚类模型[14]用来降低大数据的重复和冗余,可用于非结构化数据的聚类分析.

上述多维索引技术虽大多能在CDM上完成一定的多维查询和区间查询等功能,但大多存在索引维护代价高,解决方案较为复杂等问题,特别是当数据分布不均匀时效率普遍偏低.因此,需要改进现有索引技术或提出新的多维索引技术,使之具有较高效的偏斜数据查询功能,维护代价低,实现方案较简单等特点.

3 多维索引结构

上述CDM执行基于键值对的数据查询,支持访问数据的基本操作,但是这些数据操作不直接支持多维数据查询.为了解决多维查询的问题,本文提出了适用于CDM的多维索引结构,并实现了空间数据的范围查询.

3.1 HPR-index概述

数据被组织成一颗经过改进的均衡的桶PR四叉树,其中数据维数为d,桶容量为s,树深为m,所有叶节点都在同一层上.数据空间被均分为(2d)m-1个互相不重叠的多维超矩形.根据Hilbert曲线的编码规则,每个多维超矩形有一个唯一的键值.HPR-index建立并维护一张路由表,表中每个多维超矩形区域的键值与桶PR四叉树的叶节点一一对应.图1是二维空间数据的HPR-index的结构图,参数d=2且m=2.图1(a)中的区域被均匀分成16个小矩形,其中每个最小矩形的中心点(控制点)也就是图1(b)中四叉树的叶节点.整个矩形区域的中心点(控制点)是图1(b)中四叉树的根节点u0.这样,图1(a)的空间则被分层组织成深度m=3的一颗平衡桶四叉树,如图1(b)所示.同样,根据Hilbert的编码规则,图1(a)中区域的每个最小矩形(叶节点)均有一个唯一的Hilbert键值,如图1(c)所示.存储Hilbert键值与四叉树叶节点的路由表如图1(d)所示,从路由表中可根据键值检索到四叉树的叶节点,从而使多属性访问能有效地检索数据.

3.2 插入和删除算法

算法2用来插入一个新的数据点.首先用算法1计算出要插入数据点的子区域的Hilbert键值,然后用四叉树数据插入算法InsertToPRTree()将该数据点插入树中.数据删除算法3跟算法2相似,首先用算法1计算出要删除数据点所属的子区域的Hilbert键值,然后用四叉树数据删除算法DeleteFromPRTree()从树中删除.

图1 HPR-Index 索引结构Fig.1 Index structure of HPR-Index

算法1.SubspaceLookup(p)

输入:数据点 p=(x,y),x和y分别是点p的横坐标和纵坐标;

输出:包含点p的最小子空间的Hilbert键值.

Begin

1.i←x mod o;//o为Hilbert曲线的阶

2.j←y mod o;

3.return Hilbert(i,j);

End

算法2.InsertPoint(p)

输入:数据点 p=(x,y),x和y分别是点p的横坐标和纵坐标;

输出:插入成功标识flag.

Begin

1.key← SubspaceLookup(p);

2.flag←InsertToPRTree(key,p);

3.return flag

End

算法3.DeletePoint(p)

输入:数据点 p=(x,y),x和y分别是点p的横坐标和纵坐标;

输出:删除成功标识flag.

Begin

1.key← SubspaceLookup(p);

2.flag←DeleteFromPRTree(key,p);

3.return flag

End

3.3 分裂算法

桶PR四叉树每个节点存储的数据是有限的,当一个节点上存储的数据超过这个上限,该节点应该分裂.HPR-index要求桶PR四叉树为平衡四叉树,即所有叶节点均处于同一层,而部分叶节点的分裂会导致四叉树不平衡,因此HPR-index不允许某个叶节点单独分裂,只有在树中所有叶节点平均存储的数据达到一定的数量需要靠分裂来优化时,才进行所有叶节点的统一分裂,这样,分裂后新的叶节点仍然处于同一层.分裂的同时,Hilbert的阶也随之增加1阶.算法4是叶节点分裂的伪代码.

算法4.SplitSpace(ns)

输入:要分裂的四叉树的叶节点ns;

输出:分裂成功标识flag.

Begin //na,nb,nc,nd为叶节点ns分裂的四个子节点

1.keyOfNa←Hilbert(center points of na);

2.keyOfNb←Hilbert(center points of nb);

3.keyOfNc←Hilbert(center points of nc);

4.keyOfNd←Hilbert(center points of nd);

5.for each point p in ns do

6.if p in na then

7.pointsOfNa.add(p);

8.else if p in nb then

9.pointsOfNb.add(p);

10. else if p in nc then

11.pointsOfNc.add(p);

12. else if p in nd then

13.pointsOfNd.add(p);

14. end if

15.end for

16.flagNa←Insert(keyOfNa,pointsOfNa);

17.flagNb←Insert(keyOfNb,pointsOfNb);

18.flagNc←Insert(keyOfNc,pointsOfNc);

19.flagNd←Insert(keyOfNd,pointsOfNd);

20.if Na & Nb & Nc &Nd is true then

21.flag←ClearDataPoint(keyOfNs);

22.else flag←false;

23.return flag

End

3.4 范围查询算法

算法5是范围查询的伪代码,可用于HBase和Cassandra等云数据库.(pa,pb,pc,pd)是范围查询(查询矩形)的四个顶点.Hilbert将空间等分成网格,每个网格都有一个键值.算法5首先计算了所有与查询矩形相交的网格的坐标.GridKeys是存储包含在查询矩形范围内的网格的键值集合.每一个网格c的坐标,经过ComputeKeys()方法计算出该网格对应的Hilbert键值,并把该键值加到GridKeys列表中.然后用GetContainPoints()方法从路由表中找到网格键值对应的叶子节点,并从叶子节点中找到数据点.算法5中1-6行代码将符合矩形查询条件的键值找到;7-10行根据网格的键值,从路由表中获得叶节点信息并从叶节点把符合条件的数据取出.

图2 范围查询Fig.2 Range query

具体查询例子如图2所示,图中粉色部分是范围查询,黑色圆点是空间数据点.通过查询矩形得到与范围查询相交的网格的坐标,即{(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)};然后得到每个坐标的Hilbert键值,即{(0,1,14,3,2,13};然后根据路由表得到对应的叶节点,并从云数据库中取出数据,把不符合的数据从查询结果里删除.

算法5.RangeQuery(pa,pb,pc,pd)

输入:查询范围(查询矩形)的四个顶点pa,pb,pc,pd;

输出:查询得到的数据点集合Result.

Begin

1.Coordinate← ComputeGrid(pa,pb,pc,pd);

2.Keys← φ;

3.Result← φ;

4.for each Coordinate c ∈Coordinate do

5.GridKeys←GridKeys ∪ComputeKeys(c);

6.end for

7.for each GridKeys k ∈GridKeys do

8.Result←Result ∪GetContainPoints(k);

9.end for

10.return Result;

End

4 实验和分析

本节通过仿真实验比较三种索引技术的效率高低.这三种索引技术分别Hilbert曲线、MD-HBase(简称MD)和HPR-index(简称HPR).仿真实验的数据库版本为Cassandra1.0.10,每台物理服务器的配置为2G内存,500G硬盘,操作系统为64位的Ubuntu 8.04.4.每台物理服务器建两个虚拟节点,Cassandra环上一共运行十个虚拟节点.本实验采用的仿真数据生成器[15]能产生均匀分布和正态分布两种数据分布.得到多维均匀分布的方法仅是在每一维度上都产生均匀分布.生成多维正态分布的方法是先得到多维的均匀分布,然后用Box-Muller 算法[16]转变为服从正态分布的数据,此时参数μ=0,σ2=1.查询范围在边长为1×106数据单位的正方形内生分别生成2×105,5×105,7×105和1×106个数据单位的均匀数据集4个,正态分布数据集4个,数据集如图3(a)和图3(b)所示.为了研究数据偏斜情况下的查询效率,取上述正态分布数据集边长为1×106个数据单位的正方形坐标为A(4×105,4×105)、B(4×105,6×105)、C(6×105,6×105)、D(6×105,4×105)的四个点所围成的小正方形内的区域称为正态分布密集区,如图3(b)所示,其余区域称为正态分布稀疏区.每次实验取100次查询结果所耗费时间的平均值作为实验结果.文献[1]证明在同样的实验条件下,Hilbert阶数o=7时查询效率最高,同样条件下MD算法的参数M设置为2500时查询效率最高.因此,所有实验中将HPR和Hilbert的阶数o均设置为7,MD算法的参数M设置为2500.

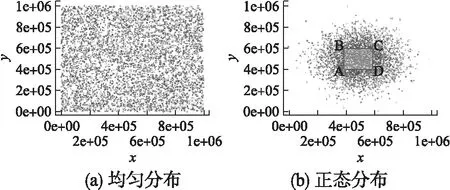
图3 数据分布Fig.3 Data distribution

4.1 不同查询范围的查询效率比较

当数据量固定为1×106而查询范围不同时,考察三种索引查询效率情况.图4给出了数据均匀分布情况下三种索引的查询效率;图5给出了数据正态分布密集区情况下三种索引的查询效率;图6给出了在数据正态分布稀疏区三种索引的查询效率.从图中可以看出,数据正态分布密集区条件下三种索引的查询时间最长,数据稀疏区三种索引的查询时间最短,数据正态分布时三种索引的查询时间介于前两者之间.查询范围越大,三种索引的查询时间越长,原因是需要读取数据的节点的数量增加.其中Hilbert在查询范围较小时查询效率与HPR相近,高于MD索引.但当查询范围较大时,Hilbert查询时间增长较快,效率急速下降.MD索引当查询范围较大时,相比Hilbert而言查询效率下降较慢,优势较明显.当查询范围不断增大时,HPR索引的查询效率优于Hilbert和MD.

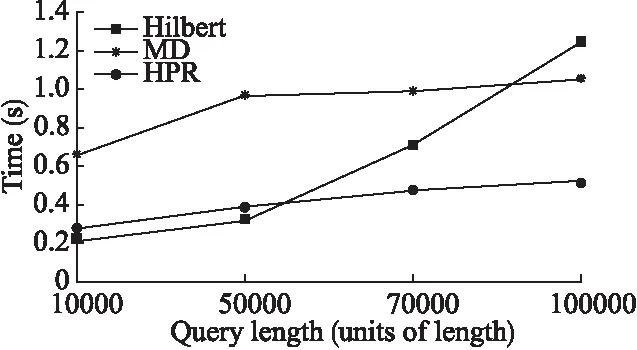
图4 数据均匀分布和不同查询范围条件下索引的查询效率Fig.4 Query efficiency of different query size under uniform distribution

图5 正态分布密集区和不同查询范围条件下索引的查询效率Fig.5 Query efficiency of different query size under Normal-dense distribution

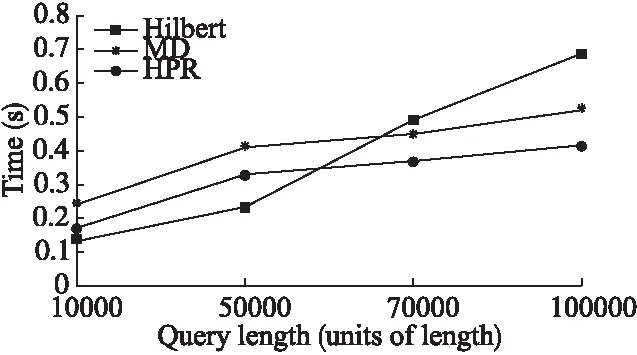
图6 正态分布稀疏区和不同查询范围条件下索引的查询效率Fig.6 Query efficiency of different query size under Normal-sparse distribution

4.2 不同数据量的查询效率比较

当数据查询范围固定为1×105时,数据量不同条件下考察三种索引查询效率情况.当数据量分为2×105、5×105、7×105和1×106时,图7给出了在数据均匀分布情况下三种索引的查询效率;图8给出了在数据正态分布密集区情况下三种索引的查询效率;图9给出了在数据正态分布稀疏区三种索引的查询效率.从图中可以看出,数据量越大,三种索引的查询时间越长,原因是需要读取数据的节点的数量增加.其中Hilbert在数据均匀分布条件下查询效率与MD相近,低于HPR索引.但当数据偏斜时,Hilbert查询时间增长较快,效率急速下降,此时MD的查询效率明显优于Hilbert,但两者均低于HPR.综上所述,当数据量不断增大时,HPR索引的查询效率优于Hilbert和MD.

4.3 插入与删除操作效率比较

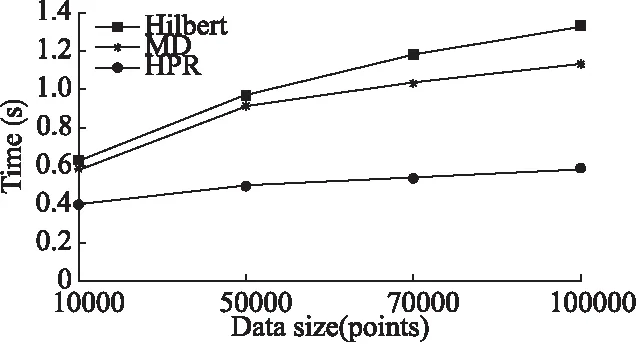
图7 数据均匀分布和不同数据量条件下的索引查询效率Fig.7 Query efficiency of different data size under uniform distribution

图8 正态分布密集区和不同数据量条件下索引的查询效率Fig.8 Query efficiency of different data size under Normal-dense distribution

图9 正态分布稀疏区和不同数据量条件下索引的查询效率Fig.9 Query efficiency of different data size under Normal-sparse distribution

图10 插入操作吞吐量比较Fig.10 Insertion throughput comparison

支持大吞吐量的数据插入操作对支撑大量基于位置的服务而言至关重要.实验通过Cassandra环上的十个虚拟节点上评估了数据插入性能.图10所示,插入吞吐量是系统负载的函数.实验将负载生成器的数量由200个增加到500个,500个增加到700个,最后增加到1000个,其中每个负载器产生每秒1000次的插入负载.实验使用参数为μ=0、σ2=1的正态分布的仿真数据集.使用仿真数据集便于调整数据的偏斜度.实验表明,三种方法均显示了良好的扩展性,插入数据吞吐量至少达到了每秒150k个空间数据点.MD索引插入吞吐量偏低的原因是因为四叉树节点分裂的开销较大,分裂一个节点MD平均需要40秒的时间.Hilbert不需要分裂节点,而HPR-index只有在特殊情况下才统一分裂所有节点,所以两者的插入吞吐量相对较高.三种索引的删除数据吞吐量均比各自的插入数据吞吐量高,如图11所示,它们的性能对比与插入数据吞吐量与图10相似.MD索引删除数据吞吐量低的原因是四叉树的合并开销较大.

5 结 论

本文提出的多维索引HPR用于在云数据管理系统Cassandra上执行范围查询.多维索引HPR用桶PR四叉树来构建基本索引结构,通过Hilbert键值来快速定位数据.此外,还设计新的空间范围查询算法、插入和删除算法.实验结果表明,多维索引HPR查询效率优于Hilbert和MD索引,尤其是在数据偏斜的情况下.

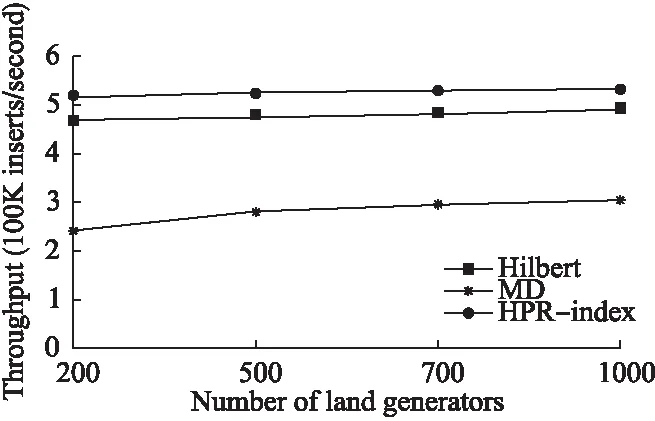
图11 删除操作吞吐量比较Fig.11 Deletion throughput comparison

：

[1] Wei Ling-yin,Hsu Ya-ting,Peng Wen-chih,et al.Indexing spatial data in cloud data managements[J].Pervasive and Mobile Computing,2014,15:48-61.

[2] Fay C,Jeffrey D,Sanjay G,et al.Bigtable:a distributed storage system for structured data[C].Proceedings of the 7th Symposium on Operating Systems Design and Implementation,CA,2006:205-218.

[3] Lakshman A,Malik P.Cassandra:a decentralized structured storage system[J].ACM SIGOPS Operating Systems Review,2010,44(2):35-40.

[4] Hanan S.Foundations of multidimensional and metric data structures[M].Beijing:Tsinghua University Press,2011:28-48.

[5] Nikolett B,Amalia D,Krisztián N,et al.Quad-kd trees:a general framework for kd trees and quad trees[J].Theoretical Computer Science,2016,616(2):126-140.

[6] Wang Jin-bao,Wu Sai,Gao Hong,et al.Indexing multi-dimensional data in a cloud system[C].Proceedings of the ACM SIGMOD/PODS Conference,2010:591-602.

[7] Shoji N,Sudipto D,Divyakant A,et al.MD-HBase:design and implementation of an elastic data infrastructure for cloud-scale location services[J].Distributed and Parallel Databases,2013,31 (2):289-319.

[8] Ma You-zhong,Meng Xiao-feng.Research on indexing for cloud

data management[J].Journal of Software,2015,26(1):145-166.

[9] Hsu Ya-ting,Pan Yi-chin,Wei Ling-yin,et al.Key formulation schemes for spatial index in cloud data managements[C].Proceedings of the 13th IEEE Conference on Mobile Data Management,2012:21-26.

[10] Zhu Xia,Luo Jun-zhou,Song Ai-bo,et al.A multi-dimensional indexing for complex query in cloud computing[J].Journal of Computer Research and Development,2013,50(8):1592-1603.

[11] Liu Xing-ping,Luo Xiang-yun,Yang Hai.Querying research on efficient traffic data cloud-indexing technology based on HBase[J].Control Engineering of China,2016,23(4):560-564.

[12] Fu Zhong-liang,Hu Yu-long,Weng Bao-feng,et,al.M-quadtree index:a spatial index method forcloud storage environment based on modified quadtree coding approach[J].Acta Geodaetica et Cartographica Sinica,2016,45(11):1342-1351.

[13] Liu Yue,Li Jin-tao,Hu Song-lin.A cost-based splitting policy search algorithm for Hive multi-dimensional index[J].Journal of Computer Research and Development,2016,53(4):798-810.

[14] Luo En-tao,Wang Guo-jun,Li Chao-liang.Research on clustering analysis of multi-dimensional remove-duplicate removal in big data[J].Journal of Chinese Computer Systems,2016,37(3):438-442.

[15] Pei Y,Zaïane O.A synthetic data generator for clustering and outlier analysis[R].Technical Report,TR06-15,Department of Computing Science,University of Alberta,2006.

[16] Box G E P,Muller M E.A note on the generation of random normal deviates[J].Annals of Mathematical Statistics,1958,29(2):610-611.

附中文参考文献：

[4] 萨姆特.多维与度量数据结构基础[M].北京:清华大学出版社,2011:28-48.

[8] 马友忠,孟小峰.云数据管理索引技术研究[J].软件学报,2015,26(1):145-166.

[10] 朱 夏,罗军舟,宋爱波,等.云计算环境下支持复杂查询的多维数据索引机制[J].计算机研究与发展,2013,50(8):1592-1603.

[11] 刘星平,罗湘运,杨 海.基于HBase的高效交通数据云索引技术[J].控制工程,2016,23(4):560-564.

[12] 付仲良,胡玉龙,翁宝凤,等.M-Quadtree索引:一种基于改进四叉树编码方法的云存储环境下空间索引方法[J].测绘学报,2016,45(11):1342-1351.

[13] 刘 越,李锦涛,虎嵩林.基于代价估计的Hive多维索引分割策略选择算法[J].计算机研究与发展,2016,53(4):798-810.

[14] 罗恩韬,王国军,李超良.大数据环境中多维数据去重的聚类算法研究[J].小型微型计算机系统,2016,37(3):438-442.