矩阵增量属性约简算法

闫 鑫，景运革

1(山西财经大学 信息管理学院，太原 030006)

2(运城学院 公共计算机教学部，山西 运城 044000)

3(西南交通大学 信息科学与技术学院，成都 611756)

1 引 言

在现实生活中，随着计算机网络、存储和通信技术迅猛的发展，许多决策信息系统的对象和属性值都会同时发生变化.例如学校里每年都会有新教师增加，同时教师的职称每年也会发生更新，如原来部分教师的职称是讲师可能会变成副教授等.针对决策信息系统对象增加且属性值发生细化问题，如何在原有数据分析的基础上快速更新变化后决策信息系统约简问题，是信息科学领域研究的一个普遍关注热点.如果使用非增量属性约简方法[1-3]来处理动态数据属性约简问题时，需要重新计算变化后决策信息系统的属性约简，不能充分利用先前知识粒度和约简，导致运行速度较慢.

为了有效解决非增量约简算法在处理动态数据时存在的缺陷，许多研究者提出了增量属性约简方法.针对决策信息系统对象变化增量属性约简问题，杨明针对决策信息系统对象集动态更新问题，对差别矩阵进行改进，分析了改进差别矩阵的增量更新机制，设计了增量属性约简算法[4]；Jiang等根据决策树自适应算法，提出了增量属性约简算法，并把所提出的增量属性约简算法应用到网络入侵数据检测中[5]；Jing针对决策信息系统对象属性集动态变化时如何快速计算约简问题，讨论了计算等价关系矩阵和相对知识粒度的增量更新原理，提出了基于对象增加时动态属性约简算法[6]； Xu等分析了一些对象增加到决策信息系统情况下属性约简的更新机理，在0-1运算的基础上，提出了一种对象集动态增加时的增量属性约简算法[8]；针对动态大数据属性约简问题，Jing等利用多粒度理论和“分而治之”方法，设计了对象变化时基于多粒度粗糙集增量属性约简算法[11]；罗来鹏根据决策信息系统对象动态增加情况，分析了二叉树增量更新机制，提出了基于对象动态增加时的增量属性约简算法[15].针对决策信息系统属性值变化增量属性约简问题，Chen等讨论了属性值变化下优势特性关系粗糙集模型中近似集更新的原理，设计了向上向下近似集及属性值约简增量更新算法[9]；Jing探讨了对象属性值变化时等价关系矩阵和相对知识粒度的增量更新机制，设计了基于属性值动态变化的增量属性约简算法[7]；针对决策表属性值发生细化问题时，唐定勇等分析了基于矩阵方法计算正域的增量更新原理，设计了属性值细化时的增量属性约简算法[10]；针对集值决策信息系统中属性值动态更新变化问题，Lang等提出了基于不可分辨矩阵的动态属性约简算法[14].根据上面分析，决策信息系统对象的属性值被细化且增加对象时增量属性约简算法研究较少.

代数中矩阵计算是一种非常有效的计算工具，已经被广泛应用到系统工程和数值分析等诸多学科领域中.针对决策信息系统对象集属性值发生细化且增加对象后如何快速更新约简的问题，首先讨论了基于矩阵方法计算决策信息系统等价关系矩阵和相对知识粒度的增量机制，然后提出了属性值细化且对象增加时增量属性约简算法，最后通过仿真实验结果表明了所提出的增量属性约简算法是有效的.

2 基于矩阵方法的非增量属性约简算法

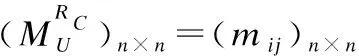
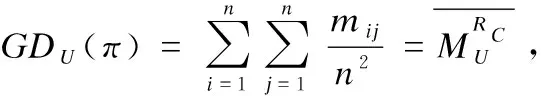
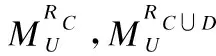
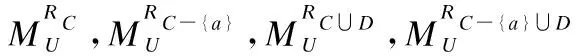
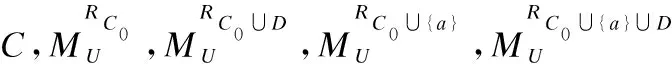
定义7[1]. 如果S=(U，A=C∪D，V，f)是决策信息系统，B⊆C，B为决策信息系统的约简当且仅当：

1)GD(D|B)=GD(D|C)；

2)对于∀a∈B，使得

GD(D|B-{a})≠GD(D|C).

根据上面的相关定义，研究者提出了一种基于矩阵方法的属性约简算法(非增量属性约简算法)[6，7，10].

3 基于矩阵方法的增量属性约简算法

当决策信息系统对象的属性值被细化且增加对象时，非增量属性约简算法计算变化后决策信息系统约简时，需要重复计算决策信息系统等价关系矩阵、相对知识粒度及约简，导致运行时间和储存空间耗费较多.为了能够快速获得变化后决策信息系统的约简，提出了属性值细化且增加对象时增量属性约简算法.

3.1 知识粒度的增量机制

定义8[10]. 如果S=(U，A=C∪D，V，f)是决策信息系统，B⊆A，B≠Ø,al∈B且Vl是条件属性al的值域，[xi]al={xi，xj∈U,|f(xi,al)=f(xj,al)}.∀xk∈[xi]al，若有f(xk，al)=v，且v∉Vl，则属性值f(xk，al)被细化为v.

假设X=[xi]al，Y={xm∈U|f(xm,al)=v}，则X-Y={xn∈U|f(xn,al)≠f(xm,al)}为条件属性al数值细化后，集合X中对象属性值没有发生变化的集合.

假设IX-Y={i|ui∈X-Y}，IY={i|ui∈Y}，则IX-Y为集合X-Y中所有元素下标的集合，IY为集合Y中所有元素下标的集合.

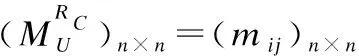
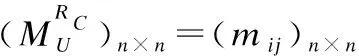
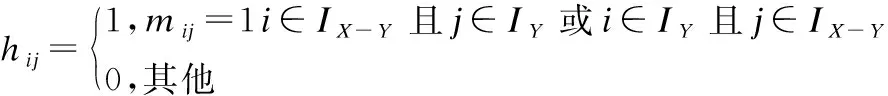
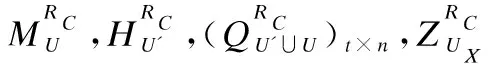
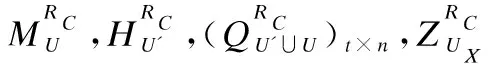
其中，Sum(…)代表矩阵所有元素的和.

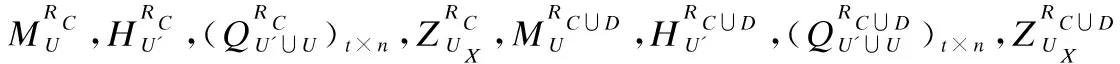
3.2 属性值细化且对象增加时基于矩阵方法的增量属性约简算法

当决策信息系统条件属性ai的数值被细化且增加了对象集UX时，根据上述的增量机制的定义和定理，在决策信息系统原来等价关系矩阵和约简的基础上，设计了属性值细化且对象增加时基于矩阵方法的增量属性约简算法，该算法的具体过程描述如下：

算法.属性值细化且对象增加时基于矩阵方法的增量属性约简算法

输入：决策信息系统S=(U，A=C∪D，V，f)，决策信息系统的约简REDU，增量对象集UX及属性ai的数值被细化；

输出：决策信息系统增加了对象集UX且属性ai的数值被细化后的约简REDU′∪UX.

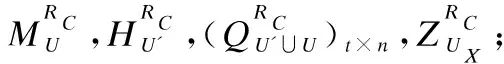
步骤2. 计算决策信息系统增加了对象集UX且属性ai的数值被细化后的相对知识粒度GDU′∪UX(D|B) ，GDU′∪UX(D|C)；

步骤3. 如果GDU′∪UX(D|B)=GDU′∪UX(D|C)，则执行步骤6，否则执行步骤4；

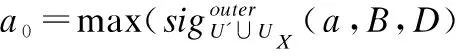
步骤5. 对于∀a∈B，计算D相对于(B-{a})的相对知识粒度GDU′∪UX(D|B-{a})，如果GDU′∪UX(D|B-{a})=GDU′∪UX(D|C)，则B←B-{a}；

步骤6.REDU′∪UX←B，输出增加对象性集UX且属性ai的数值被细化后的决策信息系统约简REDU′∪UX，算法结束.

3.3 算法复杂度分析

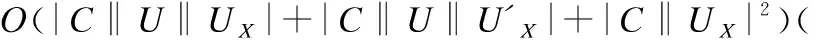
从上面分析可得增量属性约简算法的时间复杂度小于非增量属性约简算法的时间复杂度，验证了所提出的增量属性约简算法是有效的.

4 实验仿真分析

为了验证本文提出的属性值细化且增加对象时基于矩阵方法的增量属性约简算法的有效性，我们把基于矩阵方法的增量属性约简算法的运行时间和非增量属性约简算法的运行时间作比较，并下载了4组UCI数据集作为仿真实验数据集，数据集的具体描述如表1所示，实验仿真的硬件环境：CPU Pentium(R) Dual-Core E5800 3.20GHz，内存：Samsung DDR3 SDRAM，4.0GB实验仿真的软件环境：64-bit Windows 10操作系统，64-bits (JDK 1.6.0_20)和Eclipse 3.7.

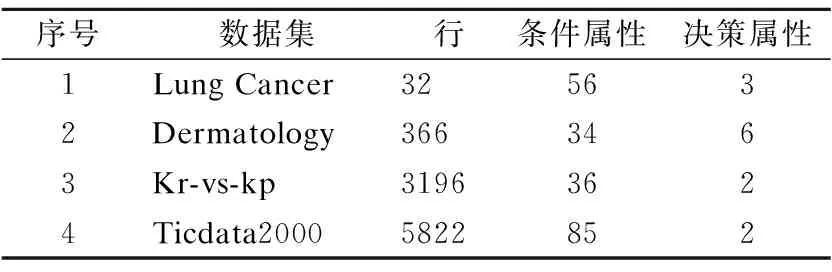
表1 数据集描述Table 1 Description of date sets

4.1 增量属性约简算法与非增量属性约简算法运行时间比较

在实验仿真过程中，我们把表1的数据按照对象均匀分成2部分，其中50%的数据集作为基本数据集，基本数据集中一半数据集20%、40%、60%、80%、100%的属性值进行细化，另一半数据集的属性值没有发生变化，剩余50%的数据按照对象的20%、40%、60%、80%、100%依次作为增量对象集，并用增量属性约简算法和非增量属性约简算法运行这些数据集，实验的仿真结果如图1中各个子图所示，纵轴表示算法的计算时间，横轴表示数据集中对象属性值发生细化且增加对象的百分数.圆形代表非增量属性约简算法的运行时间，方形代表增量属性约简算法的运行时间.

从仿真实验结果可以得出，当决策信息系统对象的属性值被细化且增加对象时，所提出的增量约简算法的计算时间远远小于非增量属性约简算法的计算时间，从而说明本文所提的属性值细化且对象增加时的增量属性约简算法是有效的.

图1 增量属性约简算法和非增量属性约简算法运行时间的比较Fig. 1 Comparison between incremental reduction method and non-incremental reduction method on computation time

4.2 增量属性约简算法与非增量属性约简算法所得约简分类精确度比较

在分类精度仿真实验中把表1的数据按照对象均匀分成两部分，其中一部分的数据作为基本数据集，另一部分作为增量数据集，当基本数据集中的一半数据集的属性值发生了细化，另一半数据集的属性值未发生变化，并把增量数据集添加到基本数据集中，分别用增量属性约简算法和非增量属性约简算法运行这些数据集.最后，运用十字交叉法和贝叶斯分类算法计算不同属性约简算法所得约简的分类精确度并对其进行分析比较，所获结果描述如表2.

表2 比较增量属性约简算法和非增量属性约简算法获得约简的分类精确度Table 2 Comparison of incremental reduction method and non-incremental reduction method on classification accuracy

从表2可以得到增量属性约简算法和非增量属性约简算法所得到约简的分类精确度的值是相近的.结果说明了，当决策信息系统对象的属性值被细化且增加对象时，本文所提出的属性值细化且对象增加时的增量属性约简算法所得到的约简是有效的.

4.3 增量属性约简算法与其他增量属性约简算法比较

在实验仿真过程中，我们把表1的数据按照对象均匀分成2部分，其中50%的数据集作为基本数据集，基本数据集中一半数据集的属性值进行细化，剩余50%的数据作为增量对象集，并用增量属性约简算法和文献[6]及文献[10]提出的增量属性约简算法运行这些数据集，实验的仿真结果如表3所示.结果表示增量属性约简算法的计算时间小于文献[6]及文献[10]提出的增量属性约简算法的计算时间.验证了所提出的增量属性约简算法在处理动态变化数据属性约简是非常有效的.

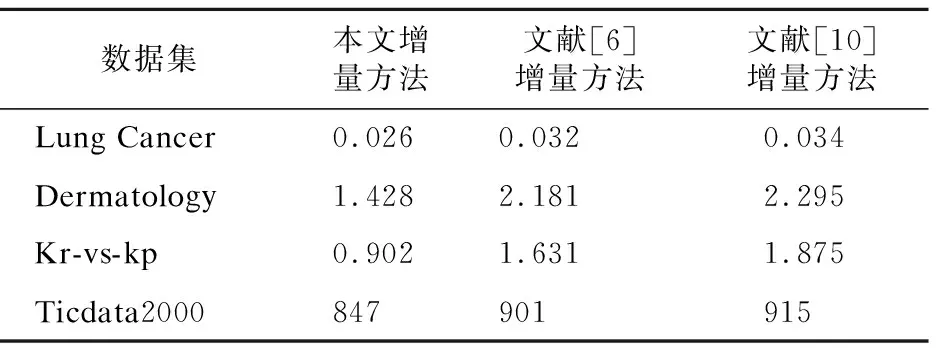
表3 增量属性约简算法和其他增量属性约简算法运行时间的比较Table 3 Comparison between incremental reduction method and other incremental reduction method on computation time

5 结束语

如何能够快速更新动态数据属性约简是信息科学领域中的研究的一个热点课题.当决策信息系统对象的属性值被细化且增加对象时，本文首先讨论了基于矩阵方法计算决策信息系统等价关系矩阵和相对知识粒度的增量机制，然后提出了属性值细化且增加对象时基于矩阵方法的增量属性约简算法，最后利用UCI数据集对所提出的增量属性约简算法进行仿真验证，仿真实验结果表明了属性值细化且增加对象时的增量属性约简算法是有效的.下一步研究将考虑在多粒度粗糙集模型下实现属性值、对象集和属性集同时变化下的增量属性约简算法来解决大数据动态环境下快速更新属性约简的问题.

：

[1] Miao Duo-qian，Fan Shi-dong.The calculation of knowledge granulation and its application[J].Systems Engineer-Theory & Practice，2002，22(1)：48-56.

[2] Wang Guo-yin，Yu Hong，Yang Da-chun.Decision table reduction based on conditional information entropy[J].Chinese Journal of Computer，2002，25(7)：760-765.

[3] Liang Ji-ye，Qu Kai-she，Xu Zong-ben.Reduction of attribute in information systems[J].Systems Engineer-Theory & Practice，2001，12(12)：76-80.

[4] Yang Ming.An incremental updating algorithm for attribute reduction based on improved discernibility matrix[J].Chinese Journal of Computer，2007，30(5)：815-822.

[5] Jiang Feng，Sui Yue-fei，Cao Cun-gen.An incremental decision tree algorithm based on rough sets and its application in intrusion detection[J].Artificial Intelligence Review，2013，40(4)：517-530.

[6] Jing Yun-ge，Li Tian-rui，Luo Chuan，et al.An incremental approach for attribute reduction based on knowledge granularity[J].Knowledge-Based Systems，2016，104(C)：24-38.

[7] Jing Yun-ge，Li Tian-rui，Huang Jun-fu，et al.A group incremental reduction approach with varying data values[J].International Journal of Intelligent Systems，2016，32(9)：1-26.

[8] Xu Yi-tian，Wang Lai-sheng，Zhang Rui-yan，et al.A dynamic attribute reduction algorithm based on 0-1 integer programming[J].Knowledge-Based Systems，2011，24(8)：1341-1347.

[9] Chen Hong-mei，Li Tian-rui，Ruan Da.Maintenance of approximations in incomplete ordered decision systems while attribute values coarsening or refining[J].Knowledge-Based Systems，2012，31(7)：140-161.

[10] Tang Ding-yong，Jing Yun-ge.A reduction algorithm of positive domain for decision table based on values refining[J].Microelectronics & Computer，2015，32(3)：23-27.

[11] Jiang Yun-ge，Li Tian-rui，Hamido Fujita，et al.An incremental attribute reduction approach based on knowledge granularity with a multi-granulation[J].Information Sciences，2017，411：23-38.

[12] Liu Qing.Rough set and rough theory[M].Beijing：Science Press，2001：7-16.

[13] Wang Lei，Ye Jun.Matrix-based approach for calculating knowledge granulation and its application in attribute reduction[J].Computer Engineering & Science，2013，35(3)：98-102.

[14] Lang Guang-ming，Li Qing-guo，Yang Tian Y.An incremental approach to attribute reduction of dynamic set-valued information systems[J].International Journal of Machine Learning and Cybernetics，2014，5(5)：775-788.

[15] Luo Lai-peng.An incremental updating algorithm for attribute reduction[J].Journal of Shenyang University (Natural Science)，2013，25(3)：246-249.

附中文参考文献：

[1] 苖夺谦，范世栋.知识粒度的计算及其应用[J].系统工程理论与实践，2002，22(1)：48-56.

[2] 王国胤，于 洪，杨大春.基于条件信息熵的决策表约简[J].计算机学报，2002，25(7)：760-765.

[3] 梁吉业，曲开社，徐宗本.信息系统的属性约简[J].系统工程理论与实践，2001，12(12)：76-80.

[4] 杨 明.一种基于改进差别矩阵的属性约简增量式更新算法[J].计算机学报，2007，30(5)：815-822.

[10] 唐定勇，景运革.一种决策表属性值细化的正域约简算法[J].微电子学与计算机，2015，32(3)：23-27.

[12] 刘 清.Rough set 及Rough推理[M].北京：科学出版社，2001：7-16.

[13] 王 磊，叶 军.知识粒度计算的矩阵方法及其在属性约简中的应用[J].计算机工程与科学，2013，35(3)：98-102.

[15] 罗来鹏.一种增量式属性约简更新算法[J].沈阳大学学报(自然科学版)，2013，25(3)：246-249.